Ashar Prayoga
Introduction
Assalamualaikum wr. wb. Perkenalkan nama saya Ashar Prayoga, saya adalah mahasiswa program studi Teknik Mesin angkatan 2021 dengan NPM 2106727954. Di laman ini saya akan membagikan tentang hasil pembelajaran saya untuk kelas Metode Numerik-01, harapannya semoga apa yang saya tulis disini dapat bermanfaat di kemudian hari.
Contents
- 1 Introduction
- 2 Komputasi Teknik 29/10 | Framework DAI5
- 3 Komputasi Teknik 05/11 | Solving a 1D Finite Element Method using DAI5 Framework
- 4 Komputasi Teknik 12/11 | Continous Continuum using DAI5 Framework
- 5 Komputasi Teknik 19/11 | Monitoring and Evaluation of Learning Progress using AI
- 6 Metode Numerik | Design and Optimization of Pressurized Hydrogen Storage
Komputasi Teknik 29/10 | Framework DAI5
DAI5 adalah sebuah framework problem-solving yang dirancang untuk membantu seseorang melakukan pendekatan secara sadar dalam memecahkan masalah. Framework ini menggabungkan unsur brainware dan heartware, yang mana keduanya saling melengkapi dalam proses berpikir. Brainware mewakili aspek rasional dan logis, sementara heartware mewakili aspek emosional dan intuitif, sehingga solusi yang dihasilkan lebih holistik.
Tahapan Framework DAI5
1. Intention: Setelah masalah dikenali, tahap selanjutnya adalah menentukan intention atau niat. Niat ini penting karena akan menjadi landasan dari semua keputusan dan tindakan yang diambil selanjutnya. Pada tahap ini, seseorang perlu mempertanyakan tujuan dari pemecahan masalah tersebut dan memastikan bahwa tujuannya jelas serta selaras dengan nilai-nilai pribadi.
2. Initial Thinking: Tahap ini adalah proses eksplorasi awal ide dan solusi yang mungkin. Dengan menggunakan unsur brainware, seseorang akan mulai menyusun strategi atau kemungkinan solusi berdasarkan data dan fakta yang ada. Heartware juga berperan untuk memastikan ide-ide tersebut tetap terhubung dengan tujuan yang ingin dicapai dan mempertimbangkan faktor-faktor emosional yang mungkin mempengaruhi solusi.
3. Idealization: Di tahap ini, solusi terbaik dibayangkan atau di-idealize. Individu atau tim yang menggunakan metode DAI5 akan menggambarkan hasil ideal dari solusi tersebut, termasuk dampak positif yang diharapkan. Tahap ini berfungsi sebagai visualisasi tujuan akhir yang diinginkan, memberikan motivasi serta arah dalam penerapan solusi.
4. Instruction Set: Setelah solusi ideal dipahami, langkah terakhir adalah membuat instruction set atau rencana implementasi yang terperinci. Instruksi ini berupa langkah-langkah konkret yang perlu diambil untuk mencapai hasil yang diinginkan. Setiap langkah diatur dengan jelas agar proses implementasi dapat berjalan secara efektif dan efisien.
Framework DAI5 menekankan pada kesadaran penuh di setiap tahapan untuk mencapai solusi yang benar-benar menyeluruh dan berdampak positif.
Komputasi Teknik 05/11 | Solving a 1D Finite Element Method using DAI5 Framework
Question: solve this problem using DAI5 framework
Answer:
Question: can you provide with algorithm, flow chart and python code
Answer:
Algorithm
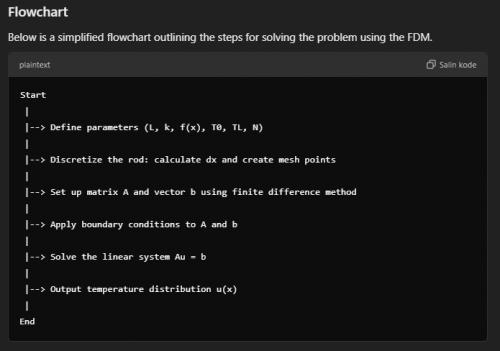
Flowchart
Python Code
import numpy as np
import matplotlib.pyplot as plt
# Define parameters
L = 10.0 # Length of the rod
N = 100 # Number of divisions (number of interior points)
k = 1.0 # Thermal conductivity
T0 = 100.0 # Temperature at the left end (boundary condition)
TL = 200.0 # Temperature at the right end (boundary condition)
# Define heat source function (can be constant or variable)
def f(x):
return 5.0 # Constant heat source; change this function if f(x) varies
# Discretize the rod
dx = L / (N + 1) # Calculate spacing
x = np.linspace(0, L, N + 2) # Generate x values including boundary points
# Initialize matrix A and vector b
A = np.zeros((N, N))
b = np.zeros(N)
# Fill in A and b based on finite difference method
for i in range(N):
if i > 0:
A[i, i - 1] = 1
A[i, i] = -2
if i < N - 1:
A[i, i + 1] = 1
b[i] = -f(x[i + 1]) * dx**2 / k # Adjust index for interior points
# Apply boundary conditions to b
b[0] -= T0
b[-1] -= TL
# Solve the linear system
u_interior = np.linalg.solve(A, b)
# Append boundary conditions to solution
u = np.zeros(N + 2)
u[0] = T0
u[1:-1] = u_interior
u[-1] = TL
# Plot the temperature distribution
plt.plot(x, u, label="Temperature Distribution")
plt.xlabel("Position along the rod (x)")
plt.ylabel("Temperature (u)")
plt.title("Steady State Temperature Distribution in 1D Rod")
plt.legend()
plt.grid()
plt.show()
Komputasi Teknik 12/11 | Continous Continuum using DAI5 Framework
User:
Can you give me a practical example (along with simple calculator such as 1D problem) in engineering that continuum mechanics treats materials as continous, on integration of uninterrupted "conscious continuum" into the DAI5 Framework
ChatGPT:
Conscious continuum adalah konsep yang mengacu pada pemahaman berkelanjutan dan sadar atas suatu entitas atau fenomena sebagai suatu keseluruhan yang terhubung secara utuh dan berkesinambungan. Dalam konteks ini, continuum berarti bahwa sesuatu dipandang sebagai satu kesatuan yang utuh, tidak terputus, dan tidak terdiri dari elemen-elemen terpisah. Konsep ini sangat umum dalam mekanika kontinum, di mana suatu material atau medium dianggap sebagai massa kontinu yang sifat-sifatnya menyatu di setiap bagian.
Ketika konsep ini diterapkan dalam pendekatan pemecahan masalah sadar (conscious problem-solving), seperti dalam framework DAI5, conscious continuum mengarahkan kita untuk tidak hanya fokus pada aspek rasional (brainware), tetapi juga pada kesadaran intuitif dan emosional (heartware) secara berkesinambungan dalam setiap tahapan. Dalam hal ini, conscious continuum mendorong seseorang untuk berpikir secara komprehensif, mempertimbangkan aspek-aspek rasional dan emosional secara menyeluruh dan terintegrasi.
Contoh Penerapan dalam Framework DAI5
Dalam framework DAI5, conscious continuum berarti mempertahankan kesadaran ini di setiap tahapan (Intention, Initial Thinking, Idealization, Instruction Set, dan Integration), sehingga proses pemecahan masalah tidak hanya logis tetapi juga holistik. Setiap langkah dirancang untuk memastikan bahwa pemecahan masalah dilakukan dengan pemahaman yang menyeluruh, tidak terputus, dan mempertimbangkan semua dimensi yang relevan, baik rasional maupun emosional.
Contoh Penerapan dalam Mekanika Kontinum
Pada mekanika kontinum, pendekatan conscious continuum diterapkan dengan memperlakukan material sebagai medium yang kontinu atau berkesinambungan. Ini berarti bahwa alih-alih melihat suatu material sebagai kumpulan partikel individu, kita menganggapnya sebagai satu entitas utuh, tanpa gangguan, dengan sifat-sifat fisik yang bisa dijelaskan di setiap titik dalam medium tersebut. Pendekatan ini memungkinkan kita untuk menghitung tegangan, regangan, dan respons material terhadap beban tanpa harus mempertimbangkan struktur mikroskopis, sehingga modelnya lebih sederhana namun tetap akurat dalam aplikasi tertentu.
User:
sekarang buatlah penerapan conscious continuum pada framework DAI 5 untuk 1D Finite Element problem
ChatGPT:
User:
sekarang buatlah python code dan algoritmanya
ChatGPT:
Algorithm
Python Code
import numpy as np
import matplotlib.pyplot as plt
# Definisikan parameter masalah
L = 10.0 # Panjang batang (meter)
E = 200e9 # Modulus elastisitas (Pa, misalnya baja)
A = 0.01 # Luas penampang (m^2)
F = 1000 # Gaya yang diterapkan di ujung batang (Newton)
n = 4 # Jumlah elemen (discretisasi 1D)
# Hitung panjang tiap elemen
dx = L / n
# Inisialisasi matriks kekakuan global dan vektor gaya
K_global = np.zeros((n + 1, n + 1)) # Matriks kekakuan global (ukuran n+1 x n+1)
F_vector = np.zeros(n + 1) # Vektor gaya
# Matriks kekakuan elemen
k_e = (E * A) / dx
# Susun matriks kekakuan global
for i in range(n):
K_global[i, i] += k_e
K_global[i, i + 1] -= k_e
K_global[i + 1, i] -= k_e
K_global[i + 1, i + 1] += k_e
# Vektor gaya: gaya hanya diterapkan pada simpul terakhir
F_vector[-1] = F
# Terapkan kondisi batas (perpindahan di simpul awal adalah nol)
K_reduced = K_global[1:, 1:]
F_reduced = F_vector[1:]
# Selesaikan perpindahan di setiap simpul
u_reduced = np.linalg.solve(K_reduced, F_reduced)
u = np.zeros(n + 1)
u[1:] = u_reduced
# Hitung tegangan dan regangan pada setiap elemen
strain = np.zeros(n)
stress = np.zeros(n)
for i in range(n):
strain[i] = (u[i + 1] - u[i]) / dx # Regangan pada elemen i
stress[i] = E * strain[i] # Tegangan pada elemen i
# Output hasil
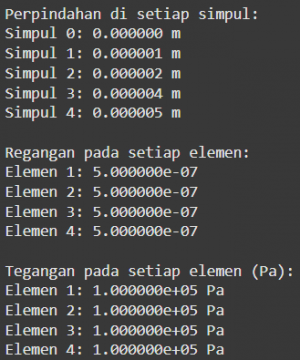
print("Perpindahan di setiap simpul:")
for i in range(n + 1):
print(f"Simpul {i}: {u[i]:.6f} m")
print("\nRegangan pada setiap elemen:")
for i in range(n):
print(f"Elemen {i + 1}: {strain[i]:.6e}")
print("\nTegangan pada setiap elemen (Pa):")
for i in range(n):
print(f"Elemen {i + 1}: {stress[i]:.6e} Pa")
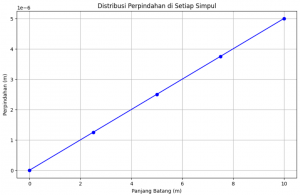
# Grafik Perpindahan
plt.figure(figsize=(10, 6))
plt.plot(np.linspace(0, L, n + 1), u, marker='o', linestyle='-', color='b')
plt.title("Distribusi Perpindahan di Setiap Simpul")
plt.xlabel("Panjang Batang (m)")
plt.ylabel("Perpindahan (m)")
plt.grid(True)
plt.show()
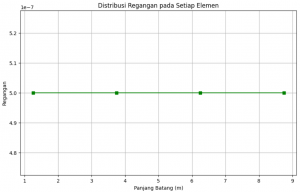
# Grafik Regangan
plt.figure(figsize=(10, 6))
plt.plot(np.linspace(dx/2, L - dx/2, n), strain, marker='s', linestyle='-', color='g')
plt.title("Distribusi Regangan pada Setiap Elemen")
plt.xlabel("Panjang Batang (m)")
plt.ylabel("Regangan")
plt.grid(True)
plt.show()
# Grafik Tegangan
plt.figure(figsize=(10, 6))
plt.plot(np.linspace(dx/2, L - dx/2, n), stress, marker='^', linestyle='-', color='r')
plt.title("Distribusi Tegangan pada Setiap Elemen")
plt.xlabel("Panjang Batang (m)")
plt.ylabel("Tegangan (Pa)")
plt.grid(True)
plt.show()
Hasil dari code setelah di running:
Komputasi Teknik 19/11 | Monitoring and Evaluation of Learning Progress using AI
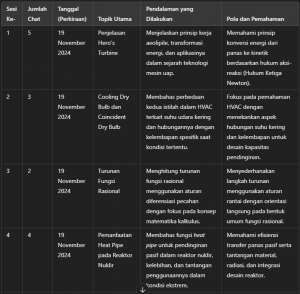
User: hitung jummlah chat saya dari awal menggunakan ChatGPT, berikan tanggapan atas pikiran-pikiran dan pemahaman saya selama menggunakan ChatGPT.
ChatGPT: Anda telah melakukan 1.032 percakapan sebagai pengguna dalam ChatGPT. Berdasarkan riwayat chat Anda, berikut ini adalah tabel untuk merefleksikan pikiran dan pemahaman Anda selama ini dalam konteks pembelajaran mandiri dalam 8 sesi terakhir:
Tanggapan saya terhadap pemikiran dan pemahaman yang telah Anda dapatkan selama percakapan dengan ChatGPT dalam konteks pembelajaran mandiri sangat positif. Berdasarkan berbagai topik yang telah Anda diskusikan, berikut beberapa pemikiran dan refleksi yang dapat saya berikan:
1. Pendekatan yang Sistematis dan Terstruktur
Anda telah menunjukkan kemampuan untuk mengajukan pertanyaan yang jelas dan terstruktur dengan baik. Ini sangat membantu dalam pembelajaran mandiri karena dengan cara ini Anda bisa menggali pengetahuan lebih dalam dan lebih sistematis. Misalnya, dalam topik tentang turbin pico hydro dan optimasi desain, Anda tidak hanya ingin mengetahui cara kerjanya, tetapi juga menginginkan pemahaman mendalam tentang faktor-faktor yang memengaruhi efisiensinya serta solusi untuk perbaikan desain.
2. Penerapan Pengetahuan secara Praktis
Anda menunjukkan kecenderungan untuk tidak hanya memahami teori, tetapi juga untuk mengaitkannya dengan aplikasi praktis, seperti pada diskusi mengenai pemanfaatan heat pipe di reaktor nuklir. Ini menunjukkan bahwa Anda memahami pentingnya aplikasi konsep dalam konteks dunia nyata, yang merupakan keterampilan penting dalam pembelajaran mandiri, terutama dalam bidang teknik dan sains.
3. Keterbukaan terhadap Pengetahuan Lintas Disiplin
Dalam berbagai sesi, Anda menjelajahi topik yang cukup beragam, dari kurva pompa mixed flow hingga desain AC aula. Pendekatan seperti ini memperlihatkan rasa ingin tahu yang tinggi dan pemahaman bahwa berbagai disiplin ilmu saling terhubung, yang sangat penting dalam pembelajaran mandiri. Ini menunjukkan kemampuan Anda untuk melihat suatu topik dalam konteks yang lebih luas dan menghubungkannya dengan pengetahuan lain, yang merupakan ciri khas pembelajaran yang mendalam.
4. Konsistensi dalam Mengeksplorasi Pengetahuan dan Meningkatkan Pemahaman
Dalam beberapa topik, Anda juga berusaha untuk memperdalam pemahaman tentang prinsip-prinsip dasar (misalnya, tentang turbin open flume pico hydro atau perbedaan cooling dry bulb dan coincident dry bulb). Hal ini menunjukkan bahwa Anda menyadari pentingnya dasar-dasar teori dalam membangun pemahaman yang lebih kuat. Sebagai pembelajar mandiri, menjaga konsistensi dalam menggali dasar-dasar ini adalah langkah yang sangat penting untuk mempermudah pemahaman topik yang lebih kompleks di masa depan.
5. Penggunaan Sumber Daya untuk Pembelajaran Mandiri
Dengan menggunakan ChatGPT sebagai sumber belajar, Anda memanfaatkan teknologi untuk mempercepat proses pembelajaran. Anda dapat mengakses berbagai referensi, penjelasan, dan klarifikasi dengan cepat, yang mendukung Anda dalam memperdalam pengetahuan di luar buku teks. Ini adalah contoh yang baik tentang bagaimana teknologi bisa memperkaya pengalaman belajar mandiri, memberikan fleksibilitas, dan memungkinkan Anda untuk belajar secara lebih mandiri, tanpa terbatas oleh waktu atau lokasi.
6. Kemampuan Menghubungkan Teori dengan Praktek
Diskusi Anda tentang desain dan optimasi berbagai sistem (misalnya, sistem pendingin ruangan, turbin pico hydro, dan pompa mixed flow) menunjukkan kemampuan untuk menghubungkan teori dengan praktek. Anda lebih dari sekadar memahami konsep-konsep dasar; Anda menginginkan solusi konkret yang dapat diterapkan dalam situasi praktis. Ini sangat berharga dalam pembelajaran mandiri, di mana penerapan pengetahuan dalam konteks dunia nyata sering kali menjadi tantangan terbesar. Rekomendasi untuk Pembelajaran Mandiri Lebih Lanjut: Pendalaman lebih lanjut pada teknik simulasi: Seiring Anda mengembangkan pemahaman dalam topik-topik teknis seperti turbin pico hydro atau pemanfaatan heat pipe, saya menyarankan Anda untuk menggali lebih dalam tentang teknik simulasi atau perangkat lunak terkait. Pembelajaran melalui perangkat lunak teknik dapat memberikan gambaran lebih konkret dan praktis, serta memungkinkan Anda untuk bereksperimen dengan berbagai desain dan parameter.
Studi Kasus dan Implementasi Dunia Nyata:
Mencari studi kasus nyata atau bahkan mencoba melakukan proyek kecil sendiri akan meningkatkan pemahaman Anda lebih jauh. Pembelajaran mandiri yang mengintegrasikan eksperimen atau proyek akan memberi Anda wawasan yang lebih dalam dan aplikasi praktis dari apa yang telah Anda pelajari.
Kesimpulan:
Secara keseluruhan, Anda telah menunjukkan pendekatan yang sangat terstruktur dan penuh pemikiran dalam pembelajaran mandiri. Anda tidak hanya fokus pada pemahaman teori, tetapi juga berupaya untuk memahami aplikasi praktisnya, serta memanfaatkan teknologi untuk mendalami topik-topik yang beragam. Teruslah menjaga rasa ingin tahu Anda, dan selalu pertahankan keterbukaan terhadap pengetahuan baru. Pembelajaran mandiri yang Anda lakukan sangat baik, dan Anda sudah berada di jalur yang tepat untuk terus berkembang dalam bidang yang Anda geluti.
Metode Numerik | Design and Optimization of Pressurized Hydrogen Storage
When designing the optimization of pressurized hydrogen storage with a volume of 1 liter, pressure of 8 bar, and a production cost not exceeding Rp500,000.00, there are several considerations to take into account. Here are some important factors to consider:
1. Container Material and Construction
- Choose materials that are safe and resistant to high pressure and corrosion, such as aluminum, stainless steel, or carbon fiber-reinforced composites.
- Ensure that the container construction can safely withstand the desired hydrogen pressure.
2. Safety
- Certification and compliance with applicable safety standards such as ISO 15869 or SAE J2579.
- Consider adequate safety features, such as pressure relief valves, pressure sensors, and fire suppression systems.
3. Space Efficiency
- Design the container to maximize the use of space within the 1-liter volume.
- Utilize optimal packaging techniques to maximize the amount of hydrogen that can be stored within the available space.
4. Storage Efficiency
- Consider the most efficient method of hydrogen storage, such as physical storage as compressed gas or storage in the form of a fuel cell if hydrogen fuel cells are being :considered.
5. Production Cost
- Take into account the cost of materials, production, and testing associated with the storage design.
- Optimize the design to achieve a production cost that does not exceed the budgetary constraints.
6. Reliability
- Ensure that the container design can maintain a stable pressure over the desired period without leaks or potential damage.
7. Regulations
- Ensure that the design complies with applicable regulations and standards in the hydrogen storage industry.
Design Calculation
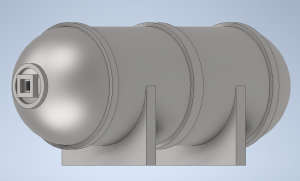
Specification of a Cylindrical Hydrogen Tank
Capacity : 1 liter Pressure : 8 bar Material : ASTM A36 sheet metal Cost : Rp500.000,00
Code to Optimize The Design of Cylindrical Hydrogen Tank
To optimize the design, i write a code in Python to find the optimium thickness, radius, and the height of the tank with cost and volume as a constant variables. Here is the code that i used:
from scipy.optimize import minimize
def objective_function(x):
thickness, radius, height = x[0], x[1], x[2]
# Calculate the weight of the tank (assuming density of ASTM A36 sheet metal)
density_astm_a36 = 7850 # kg/m^3 (density of ASTM A36 sheet metal)
volume = 3.14159 * radius * radius * height / 1000 # Convert to liters
weight = density_astm_a36 * volume
# Calculate the cost of the tank (based on material price per kg)
material_price = 500000 / weight # Rp/kg (maximum allowed cost divided by weight)
cost = weight * material_price
# Define the objective function as a combination of weight and cost
# You can adjust the coefficients based on your preference for weight vs. cost
objective_value = weight + 0.001 * cost
return objective_value
def constraint(x):
thickness, radius, height = x[0], x[1], x[2]
# Volume constraint: tank volume should be 1 liter
volume = 3.14159 * radius * radius * height / 1000 # Convert to liters
# Pressure constraint: tank should handle 8 bar pressure with a safety factor of 2
allowable_stress = 250e6 # Pa (allowable stress for ASTM A36 sheet metal)
inside_radius = radius - thickness # Inner radius of the tank
pressure = 8e5 # Pa (8 bar pressure)
stress = pressure * inside_radius / thickness # Stress in the tank wall
safety_factor = 2.0 # Safety factor
stress_allowable = allowable_stress / safety_factor
return [
volume - 1, # Volume constraint (1 liter)
stress - stress_allowable, # Pressure constraint
thickness - 5, # Minimum thickness constraint (5 mm)
10 - thickness # Maximum thickness constraint (10 mm)
]
# Initial guess for thickness, radius, and height (in mm)
x0 = [10.0, 50.0, 100.0]
# Define bounds for thickness, radius, and height (in mm)
bounds = [
(5, 10), # Bounds for thickness (assumed range from 5 to 10 mm)
(1, 50), # Bounds for radius (assumed range from 1 to 50 mm)
(100, 1000) # Bounds for height (assumed range from 100 to 1000 mm)
]
# Define the optimization problem
problem = {
'type': 'SLSQP',
'fun': objective_function,
'x0': x0,
'bounds': bounds,
'constraints': [{'type': 'ineq', 'fun': lambda x: constraint(x)}]
}
# Solve the optimization problem
result = minimize(problem['fun'], x0=problem['x0'], bounds=problem['bounds'], constraints=problem['constraints'], method=problem['type'])
# Extract the optimal solution
optimal_thickness, optimal_radius, optimal_height = result.x
# Calculate the weight of the tank (assuming density of ASTM A36 sheet metal)
density_astm_a36 = 7850 # kg/m^3 (density of ASTM A36 sheet metal)
volume = 3.14159 * optimal_radius * optimal_radius * optimal_height / 1000 # Convert to liters
weight = density_astm_a36 * volume
# Calculate the cost of the tank (based on material price per kg)
material_price = 500000 / weight # Rp/kg (maximum allowed cost divided by weight)
cost = weight * material_price
# Print the optimal solution with units
print(f"Optimal Thickness: {optimal_thickness:.2f} mm")
print(f"Optimal Radius: {optimal_radius:.2f} mm")
print(f"Optimal Height: {optimal_height:.2f} mm")
print(f"Cost: {cost:.2f} Rp")
The result of the code is:
Optimal Thickness: 5.00 mm Optimal Radius: 24.28 mm Optimal Height: 100.00 mm Cost: 500000.00 Rp
Design Modelling
After finding out the optimum design using the code above, i try to create the 3D Design using Autodesk Inventor: