Difference between revisions of "Ashar Prayoga"
| Line 62: | Line 62: | ||
import numpy as np | import numpy as np | ||
import matplotlib.pyplot as plt | import matplotlib.pyplot as plt | ||
| − | |||
# Define parameters | # Define parameters | ||
L = 10.0 # Length of the rod | L = 10.0 # Length of the rod | ||
| Line 69: | Line 68: | ||
T0 = 100.0 # Temperature at the left end (boundary condition) | T0 = 100.0 # Temperature at the left end (boundary condition) | ||
TL = 200.0 # Temperature at the right end (boundary condition) | TL = 200.0 # Temperature at the right end (boundary condition) | ||
| − | |||
# Define heat source function (can be constant or variable) | # Define heat source function (can be constant or variable) | ||
def f(x): | def f(x): | ||
return 5.0 # Constant heat source; change this function if f(x) varies | return 5.0 # Constant heat source; change this function if f(x) varies | ||
| − | |||
# Discretize the rod | # Discretize the rod | ||
dx = L / (N + 1) # Calculate spacing | dx = L / (N + 1) # Calculate spacing | ||
x = np.linspace(0, L, N + 2) # Generate x values including boundary points | x = np.linspace(0, L, N + 2) # Generate x values including boundary points | ||
| − | |||
# Initialize matrix A and vector b | # Initialize matrix A and vector b | ||
A = np.zeros((N, N)) | A = np.zeros((N, N)) | ||
b = np.zeros(N) | b = np.zeros(N) | ||
| − | |||
# Fill in A and b based on finite difference method | # Fill in A and b based on finite difference method | ||
for i in range(N): | for i in range(N): | ||
| Line 90: | Line 85: | ||
A[i, i + 1] = 1 | A[i, i + 1] = 1 | ||
b[i] = -f(x[i + 1]) * dx**2 / k # Adjust index for interior points | b[i] = -f(x[i + 1]) * dx**2 / k # Adjust index for interior points | ||
| − | |||
# Apply boundary conditions to b | # Apply boundary conditions to b | ||
b[0] -= T0 | b[0] -= T0 | ||
b[-1] -= TL | b[-1] -= TL | ||
| − | |||
# Solve the linear system | # Solve the linear system | ||
u_interior = np.linalg.solve(A, b) | u_interior = np.linalg.solve(A, b) | ||
| − | |||
# Append boundary conditions to solution | # Append boundary conditions to solution | ||
u = np.zeros(N + 2) | u = np.zeros(N + 2) | ||
| Line 103: | Line 95: | ||
u[1:-1] = u_interior | u[1:-1] = u_interior | ||
u[-1] = TL | u[-1] = TL | ||
| − | |||
# Plot the temperature distribution | # Plot the temperature distribution | ||
plt.plot(x, u, label="Temperature Distribution") | plt.plot(x, u, label="Temperature Distribution") | ||
Revision as of 16:32, 4 November 2024
Introduction
Assalamualaikum wr. wb. Perkenalkan nama saya Ashar Prayoga, saya adalah mahasiswa program studi Teknik Mesin angkatan 2021 dengan NPM 2106727954. Di laman ini saya akan membagikan tentang hasil pembelajaran saya untuk kelas Metode Numerik-01, harapannya semoga apa yang saya tulis disini dapat bermanfaat di kemudian hari.
Framework DAI5
DAI5 adalah sebuah framework problem-solving yang dirancang untuk membantu seseorang melakukan pendekatan secara sadar dalam memecahkan masalah. Framework ini menggabungkan unsur brainware dan heartware, yang mana keduanya saling melengkapi dalam proses berpikir. Brainware mewakili aspek rasional dan logis, sementara heartware mewakili aspek emosional dan intuitif, sehingga solusi yang dihasilkan lebih holistik.
Tahapan Framework DAI5
1. Intention: Setelah masalah dikenali, tahap selanjutnya adalah menentukan intention atau niat. Niat ini penting karena akan menjadi landasan dari semua keputusan dan tindakan yang diambil selanjutnya. Pada tahap ini, seseorang perlu mempertanyakan tujuan dari pemecahan masalah tersebut dan memastikan bahwa tujuannya jelas serta selaras dengan nilai-nilai pribadi.
2. Initial Thinking: Tahap ini adalah proses eksplorasi awal ide dan solusi yang mungkin. Dengan menggunakan unsur brainware, seseorang akan mulai menyusun strategi atau kemungkinan solusi berdasarkan data dan fakta yang ada. Heartware juga berperan untuk memastikan ide-ide tersebut tetap terhubung dengan tujuan yang ingin dicapai dan mempertimbangkan faktor-faktor emosional yang mungkin mempengaruhi solusi.
3. Idealization: Di tahap ini, solusi terbaik dibayangkan atau di-idealize. Individu atau tim yang menggunakan metode DAI5 akan menggambarkan hasil ideal dari solusi tersebut, termasuk dampak positif yang diharapkan. Tahap ini berfungsi sebagai visualisasi tujuan akhir yang diinginkan, memberikan motivasi serta arah dalam penerapan solusi.
4. Instruction Set: Setelah solusi ideal dipahami, langkah terakhir adalah membuat instruction set atau rencana implementasi yang terperinci. Instruksi ini berupa langkah-langkah konkret yang perlu diambil untuk mencapai hasil yang diinginkan. Setiap langkah diatur dengan jelas agar proses implementasi dapat berjalan secara efektif dan efisien.
Framework DAI5 menekankan pada kesadaran penuh di setiap tahapan untuk mencapai solusi yang benar-benar menyeluruh dan berdampak positif.
Solving a 1D Finite Element Method using DAI5 Framework
Question: solve this problem using DAI5 framework
Answer:
Question: can you provide with algorithm, flow chart and python code
Answer:
Algorithm
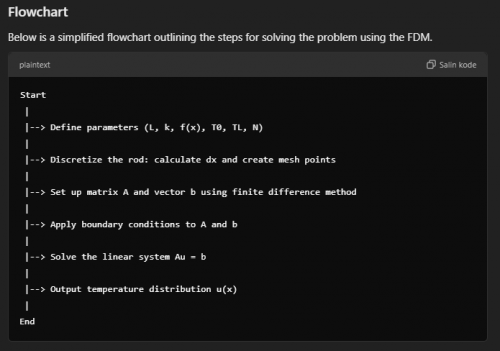
Flowchart
Python Code
import numpy as np
import matplotlib.pyplot as plt
# Define parameters
L = 10.0 # Length of the rod
N = 100 # Number of divisions (number of interior points)
k = 1.0 # Thermal conductivity
T0 = 100.0 # Temperature at the left end (boundary condition)
TL = 200.0 # Temperature at the right end (boundary condition)
# Define heat source function (can be constant or variable)
def f(x):
return 5.0 # Constant heat source; change this function if f(x) varies
# Discretize the rod
dx = L / (N + 1) # Calculate spacing
x = np.linspace(0, L, N + 2) # Generate x values including boundary points
# Initialize matrix A and vector b
A = np.zeros((N, N))
b = np.zeros(N)
# Fill in A and b based on finite difference method
for i in range(N):
if i > 0:
A[i, i - 1] = 1
A[i, i] = -2
if i < N - 1:
A[i, i + 1] = 1
b[i] = -f(x[i + 1]) * dx**2 / k # Adjust index for interior points
# Apply boundary conditions to b
b[0] -= T0
b[-1] -= TL
# Solve the linear system
u_interior = np.linalg.solve(A, b)
# Append boundary conditions to solution
u = np.zeros(N + 2)
u[0] = T0
u[1:-1] = u_interior
u[-1] = TL
# Plot the temperature distribution
plt.plot(x, u, label="Temperature Distribution")
plt.xlabel("Position along the rod (x)")
plt.ylabel("Temperature (u)")
plt.title("Steady State Temperature Distribution in 1D Rod")
plt.legend()
plt.grid()
plt.show()