Uts andru
NOMER 1a, andru
pada soal ini akan menghitung tentang tengangan tali dengan itu kita mempunyai beberapa variable yaitu massa pada batang dan percepatan pada batang dengan persoalan pada nomer 1a behubungan dengan hukum newton Σ F = 0
maka saya akan memulai memsaukan koding import numpy as np class GEPP():
def __init__(self, A, b, doPricing=True):
self.A = A
self.b = b
self.doPricing = doPricing
self.n = None
self.x = None
self._validate_input()
self._elimination()
self._backsub()
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
"""
k represents the current pivot row. Since GE traverses the matrix in the
upper right triangle, we also use k for indicating the k-th diagonal
column index.
:return
"""
for k in range(self.n - 1):
if self.doPricing:
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[1., 1., 2., 2.],
[-2., 1., -1., 1.],
[0., 0., 1., 1.],
[0., 0., 0., 1.]])
b = np.array([[20.],
[20.],
[20.],
[20.]])
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
DENGAN HASIL TERSEBUT MAKA KITA DAPAT MEGETAHUI TEGANGAN TALI YANG ADA PADA SOAL TERSEBUT MAKA HASIL 'RUN MODULE' NYA ADALAH
[ -6.66666667 -13.33333333 0. 20. ] [[1. 1. 2. 2.]
[0. 3. 3. 5.] [0. 0. 1. 1.] [0. 0. 0. 1.]]
[[20.]
[60.] [20.] [20.]]
NOMER 1b , andru
maka pada soal kali ini berhubungan dengan hukum newton kedua yaitu Σ F = m × a.
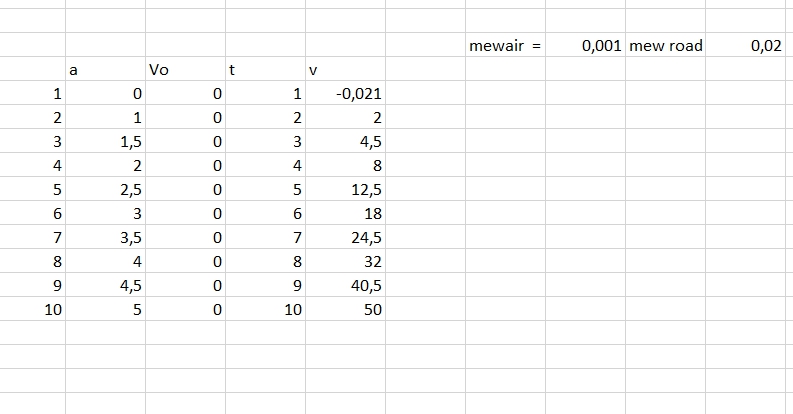
pada nomer 1b ini mencari v pada t detik. saya mengunakan program exel excel dengan memmasukan nilai- nilai Vo, a , t, dan mew gesek.
=D6+(C6*E6)-I4
hasil V trlihat