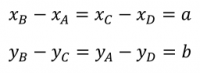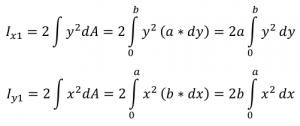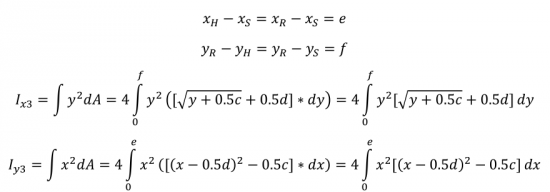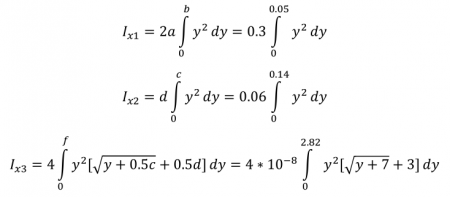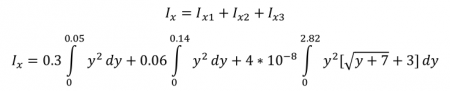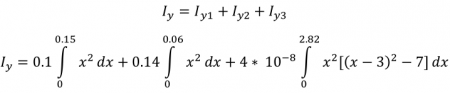Tugas UTS Ismail
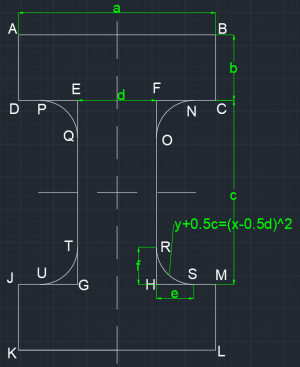
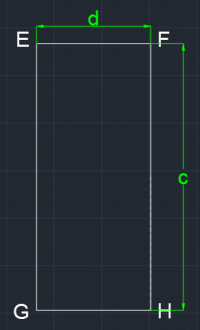
Akan dicari inersia ke arah x (I x ) dan inersia ke arah y (I y ) untuk sebuah permukaan benda di gambar 1. Untuk mencari inersia tersebut, benda dibagi menjadi beberapa bagian. Hal tersebut dikarenakan inersia bersifat skalar sehingga hasil dapat dihitung dengan artimatika biasa. Bagian-bagian yang dihitung adalah:
Contents
[hide]Bagian 1
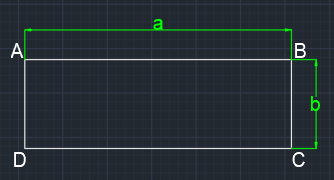
Bagian 1 memiliki bentuk persegi panjang dengan luas a x b. Selain balok ABCD, balok yang juga merupakan bagian I adalah balok JKLM. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 1 adalah:
Bagian 2
Bagian 2 memiliki bentuk persegi panjang dengan luas c x d. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 2 adalah:
Bagian 3
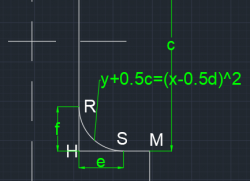
Bagian 3 memiliki bentuk berupa fungsi f(x) = (x-0.5d)2 - 0.5c dari titik xH ke xS dan yR ke yH. Selain balok HRS, balok yang juga merupakan bagian 3 adalah balok GTU, EPQ dan FNO. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 3 adalah:
Total
Setelah dicari inersia untuk tiap bagian, kemudian inersia dijumlah sehingga nilai Ix dan Iy untuk gambar 1 adalah:
Contoh Soal
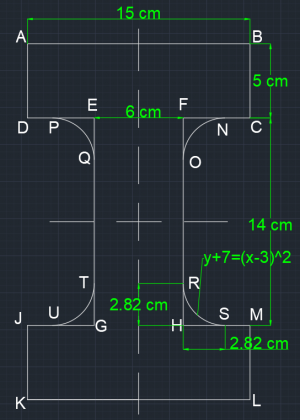
Diketahui:
- a = 15 cm = 0.15 m
- b = 5 cm = 0.05 m
- c = 14 cm = 0.14 m
- d = 6 cm = 0.06 m
- e = f = 2.82 cm = 0.0282 m
- f(x)HRS, GTU, EPQ, FNO= (x – 3)2 – 7
Ditanya: Ix dan Iy balok kolom?
Dijawab:
Flowchart pengerjaan
Inersia pada sumbu x
Sehingga Ix untuk balok kolom tersebut adalah
Inersia pada sumbu y
Sehingga I x untuk balok tersebut adalah
Inersia pada sumbu y
Setelah perumusan Ix dan Iy didapat, maka rumus-rumus yang telah dimodelkan akan diselesaikan dengan menggunakan software EES. Input yang dimasukkan adalah:
{definisi parameter}
a = 0.15 "dalam meter"
b = 0.05 "dalam meter"
c = 0.14 "dalam meter"
d = 0.06 "dalam meter"
e = 2.82 "dalam centimeter"
f = 2.82 "dalam centimeter"
{mencari Ix}
Ix1=integral(2*a*y1^2,y1,0,b)
Ix2=integral(d*y2^2,y2,0,c)
Ix3=integral(4*10^(-8)*(y3^2)*((y3+0.5*c)^0.5+0.5*d),y3,0,f)
Ix=Ix1+Ix2+Ix3
{selesai mencari Ix}
{mencari Iy}
Iy1=integral(2*b*x1^2,x1,0,a)
Iy2=integral(c*x2^2,x2,0,d)
Iy3=integral(4*10^(-8)*(x3^2)*((x3-0.5*d)^2-0.5*c),x3,0,e)
Iy=Iy1+Iy2+Iy3
{selesai mencari Iy}
{
CATATAN:
Rumus integral => integral(fungsi, variable yang ingin diintegralkan, batas bawah, batas atas)
Jadi, jika fungsi pada bagian 3 ingin dirubah, cukup hanya merubah "fungsi" pada Ix3 dan Iy3. Dalam hal ini, fungsi 3 hasilnya adalah cm^4 sehingga perlu diconvert ke m^4 dengan mengalikan 10^-8 pada persamaan.
}
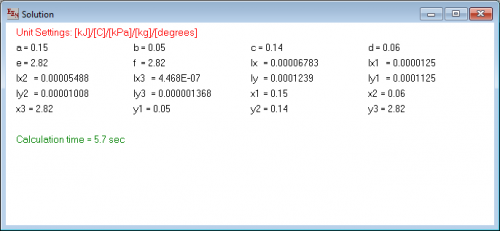
Hasil
Dari hasil iterasi yang dilakukan EES, didapatkan hasil Ix dan Iy untuk balok kolom adalah
- Ix = 6.783 x 10-5 m4
- Iy = 1.239 x 10-4 m4
dengan hasil inersia untuk masing-masing bagian adalah
Bagian 1:
Ix1 = 1.25 x 10-5 m4 Iy1 = 1.125 x 10-4 m4
Bagian 2:
Ix2 = 5.488 x 10-5 m4 Iy2 = 1.008 x 10-5 m4
Bagian 3:
Ix3 = 4.468 x 10-7 m4 Iy3 = 1.368 x 10-6 m4