Tugas 2 metode numerik arief muhammad
Tugas 1 Interpolasi
Pada pertemuan kedua tanggal 14 Februari 2020, Pak Dai memberi tugas untuk mencari dan menyelesaikan permasalahan yang ada di buku Jaan Kiusalaas Numerical Methods in Engineering. Mahasiswa diminta untuk memilih 1 soal dari 1 bab yang ada di buku tersebut. Saya sendiri memilih soal ini yang terdapat di bab 3, yaitu Linear Interpolation.
Linear Interpolation sering ditemui di beberapa Mata Kuliah seperti Struktur Kapal dan Tugas Merancang Kapal. Interpolasi digunakan karena di kondisi tertentu, data yang dicari tidak tersedia di penampang grafik.
Disini saya mencoba menggunakan cara manual, yang rumusannya tersedia di banyak referensi.
Untuk mencari nilainya, saya menggunakan rumus (X-X1)/(X2-X1) = (Y-Y1)/(Y2-Y1). Dengan X = nilai yang dicari, X1 = batas bawah nilai yang dicari, X2 = batas atas nilai yang dicari. Y = Nilai yang diketahui, Y1 = Batas bawah nilai yang diketahui, Y2 = Batas atas nilai yang diketahui.
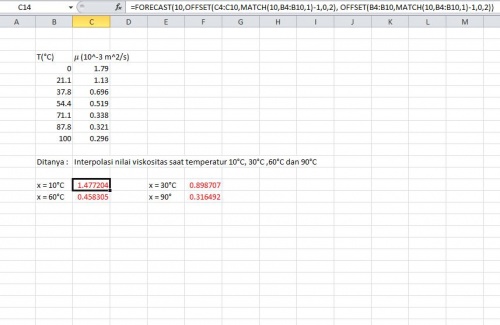
Selain cara manual, interpolasi linear juga dapat dikerjakan dengan menggunaka software. Pada kesempatan ini, saya menggunakan software excel. Setelah memasukkan data yang dibutuhkan, kemudian meng-input formulasi yang digunakan di excel yaitu =FORECAST(NewX,OFFSET(KnownY,MATCH(NewX,KnownX,1)-1,0,2), OFFSET(KnownX,MATCH(NewX,KnownX,1)-1,0,2)). Kemudian mengganti notasi "NewX" dengan nilai yang dicari (ex 10 derajat). "KnownY" dan "KnownX" sebagai unsur yang diketahui. Setelah melakukan operasi Excel, nilai yang didapat sama persis.
Tugas 2 Intial Problem
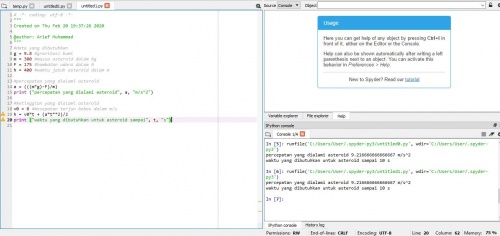
Untuk mencari estimasi waktu yang dibutuhkan untuk asteroid sampai ke bumi, digunakan rumus h = v0*t + 1/2*at^2. Tetapi sebelum itu, percepatan asteroid harus diketahui dengan menggunakan rumus F = m*a yang diturunkan menjadi W - fgesek = m*a dengan W = m*g. Setelah melakukan perhitungan, didapati waktu yang dibutuhkan asteroid sampai di bumi adalah sekitar t = 9.31 s
Sedangkan untuk menggunakan metode Spyder Annaconda, data yang terkait langsung dimasukkan. Untuk melihat hasilnya, input perintahnya adalah print ("waktu yang dibutuhkan hingga asteroid sampai", t, "s")