Tugas 1 Muhammad Akha Dewantoro

1. Jelaskan konsep “Infinite”

Ketakterhinggaan adalah sebuah konsep penting yang melambangkan realitas yang menunjukkan kekuasaan Allah SWT yang tak terbatas. Kata infinity berasalh dari Bahasa Latin infinitas yang berarti tak terhingga. Pada masa Yunani kuno, konsep ketakterhinggaan dalam dunia nyata dapat diamati melalui tiga hal yaitu: waktu yang terlihat tak berujung, ruang dan waktu yang bersifat tak ada akhirnya jika dibagi dan ruang itu tidak memiliki batas. Pada 490 BC – 430 BC, seorang filsuf Yunani, Zeno of Elea mengemukakan beberapa paradoks yang salah satunya terkenal adalah perlombaan lari antara Achilles dan kura-kura. Paradoks Zeno lain yang terkenal adalah ‘Dikhotomi’, ‘Anak Panah’, ‘Gerakan orang berurutan’. Namun, pada 384 SM – 322 SM, Aristoteles yakin terhadap keberhinggaan hingga menghindari kenyataan tentang ketakterhinggaan dengan mendefinisikan potentially infinity. Hal ini ditentang oleh Thabit Ibn Qurra (836-901 M) yang percaya adanya actual infinity. Albert Saxony (1350 M) menunjukkan bahwa seseorang dapat membuat himpunan tak hingga dan menyusunnya sehingga menjadi himpunan yang besar dan tidak terbatas sebagaimana himpunan tak hingga. Sehingga, Nicole Oresme pada 1350 M menjadi matematikawan pertama yang membuktikan divergensi dari deret harmonik berikut:

Pada tahun 1600, Galileo menyarankan penyertaan bilangan tak hingga. Dia mengatakan “Suatu kesalahan jika berkata bahwa kuantitas dari tak hingga lebih besar atau lebih kecil atau sama dengan bilangan lain”. Sehingga John Wallis pada tahun 1655 memberi simbol ∞, yang menandakan sebuah kurva yang tak berujung. Georg Cantor (1845-1918) mengungkapkan dalam salah satu tulisannya “Tuhan maha sempurna, seseorang bisa menyimpulkan bahwa adalah sangat udah bagi Tuhan untuk membuat transfinitum ordinatum.

Sumber: Sabirin, Muhamad. Konsep Ketakhinggaan dalam Matematika. 2014. Volume 2, Nomor 1, hlm 1-7. EDU-MAT Jurnal Pendidikan Matematika.

2. Menjelaskan Persamaan

Bagaimana anda menjelaskan secara rasional atas pertanyaan berapa nilai ((x^2-1))/((x-1));x=1?

Pada contoh kasus soal diatas, penyelesaian menggunakan metode eksak dikarenakan nilai x=1 tidak dapat dimuat begitu saja. Kasus ini dapat diselesaikan menggunakan pendekatan limit. Berikut adalah contoh perhitungannya.

Untuk x=1,

Nilai y=2

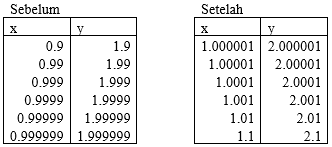
Konsep ini dapat digantikan dengan perhitungan numerik dengan melakukan perhitungan yang bersifat mendekati baik sebelum maupun sesudah nilai n. Berikut adalah nilai hasil perhitungan dari beberapa nilai yang mendekati.