Problem set 2.1 No.6

import numpy as np

1. 1. definisi matriks

A = np.array ([[1,2,0,-2,0], [0,1,0,2,-1], [0,0,2,1,2], [0,0,0,-1,1], [0,1,-1,1,-1]], float) B = np.array ([1,1,-4,-2,-1], float)

n = len(A)

1. 2. eliminasi gauss

for k in range (0,n-1) : #k adalah baris pivot dimulai dari 0 sampai n-1

   for i in range (k+1, n) : #i adalah baris dibawah pivot sampai terakhir
       if A[i,k]!=0 :
           lam = A[i,k]/A[k,k]
           A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
           B[i] = B[i]-(B[k]*lam)

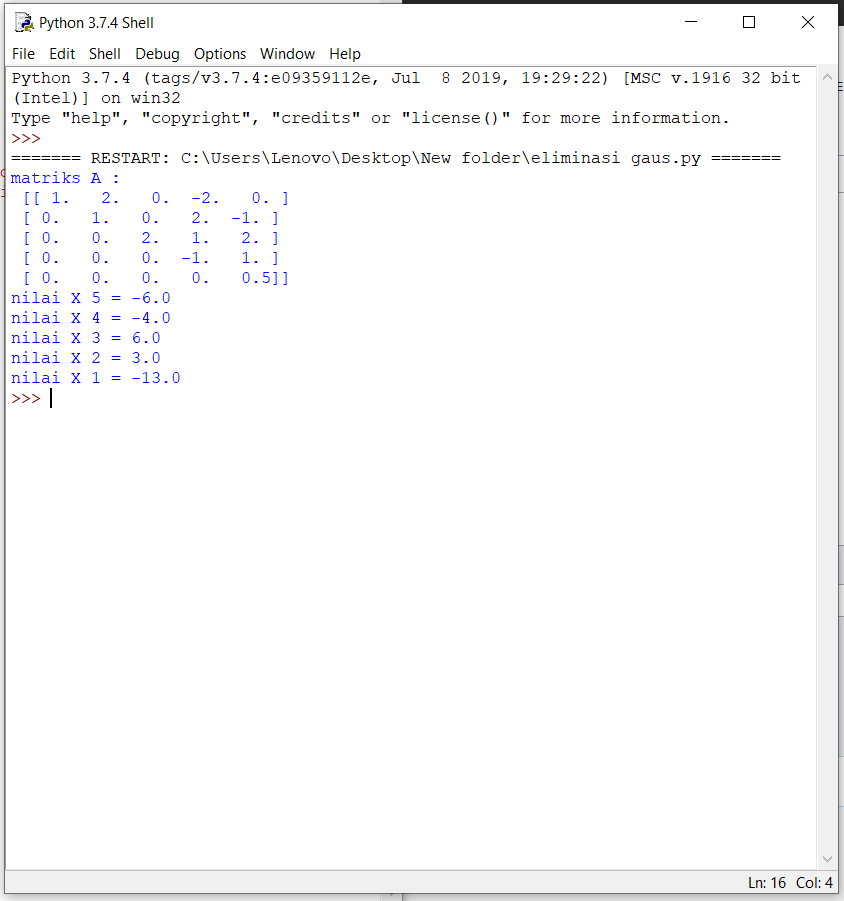
print ('matriks A :', '\n', A)

1. 3. back substitution

x=np.zeros (n,float) #menyatakan kalo dia matrix for m in range (n-1, -1, -1) : #m dari bawah ke atas

   x[m] = (B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m]
   print ('nilai X', m+1, '=', x[m])