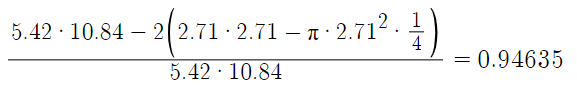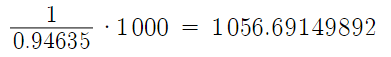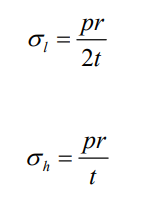Pressurized Hydrogen Storage Optimization
Contents
Pressurized Hydrogen Storage Optimization
Tugas : Merancang dan mengoptimalkan tangki penyimpanan hidrogen bertekanan 1 liter (8 bar)
Dalam merancang konsep tangki hidrogen dengan kapasitas 1 liter, tekanan 8 bar, dan biaya produksi maksimal Rp. 500.000, berikut adalah beberapa langkah dan pertimbangan yang perlu diperhatikan:
Pemilihan Bahan Tangki: Pertimbangkan penggunaan bahan yang kuat dan ringan, seperti aluminium atau serat karbon, untuk meminimalkan biaya produksi dan memenuhi persyaratan kekuatan. Pastikan bahan tersebut mampu menahan tekanan 8 bar dengan aman.
Desain dan Ukuran Tangki: Merancang tangki dengan ukuran dan bentuk yang tepat untuk memuat kapasitas 1 liter hidrogen dan menahan tekanan 8 bar. Pertimbangkan untuk mengoptimalkan ukuran tangki agar dapat mengurangi penggunaan bahan dan mengendalikan biaya produksi.
Konstruksi dan Pengelasan: Pastikan tangki dirancang dengan sambungan yang kuat dan aman. Gunakan metode pengelasan seperti TIG (Tungsten Inert Gas) atau MIG (Metal Inert Gas) yang sesuai untuk menggabungkan bagian-bagian tangki. Selalu patuhi standar keamanan dalam proses pengelasan.
Sistem Penguncian dan Penyegelan: Pastikan tangki dilengkapi dengan sistem penguncian yang efektif untuk mencegah kebocoran hidrogen. Lakukan pemeriksaan dan pengujian kebocoran secara menyeluruh untuk memastikan tangki dapat mempertahankan tekanan yang diinginkan selama penggunaan.
Perlindungan dan Keamanan: Sertakan sistem perlindungan dan katup pelepas tekanan untuk mengurangi risiko kegagalan dan kelebihan tekanan pada tangki. Perhatikan faktor keamanan yang sangat penting dalam perancangan tangki hidrogen.
Biaya Produksi: Selama merancang tangki, perhatikan biaya produksi secara keseluruhan agar tetap berada dalam batas maksimal Rp. 500.000. Pilih bahan dan metode konstruksi yang efisien untuk mencapai tujuan ini. Hitunglah biaya bahan, biaya tenaga kerja, dan biaya produksi lainnya dengan cermat.
Selain itu, penting untuk memperhatikan manajemen risiko dalam merancang tangki hidrogen. Beberapa pertimbangan yang dapat diikuti antara lain:
Identifikasi Risiko: Lakukan identifikasi risiko yang terkait dengan tangki hidrogen, seperti kebocoran hidrogen, kegagalan struktural, kelebihan tekanan, atau reaksi kimia yang tidak diinginkan. Perhatikan juga faktor-faktor lingkungan dan keamanan yang relevan.
Analisis Risiko: Lakukan analisis risiko secara sistematis untuk menilai probabilitas dan dampak setiap risiko yang diidentifikasi. Prioritaskan risiko berdasarkan tingkat keparahan dan kemungkinan terjadinya.
Mitigasi Risiko: Berdasarkan hasil analisis risiko, buat rencana mitigasi yang efektif untuk mengurangi risiko yang diidentifikasi. Misalnya, implementasikan sistem deteksi kebocoran hidrogen yang sensitif, pilih material dengan kekuatan yang sesuai, dan sertakan perangkat pelepas tekanan yang terpercaya.
Material Tangki: Pilih material yang cocok untuk tangki hidrogen dengan mempertimbangkan faktor risiko. Pastikan material tersebut tahan terhadap korosi dan embrittlement akibat hidrogen. Lakukan pengujian material secara menyeluruh untuk memastikan kesesuaiannya.
Desain Struktural: Rancang struktur tangki dengan mempertimbangkan kekuatan, keamanan, dan risiko terkait. Gunakan metode analisis struktural seperti finite element analysis (FEA) untuk memastikan kekuatan dan integritas struktural yang memadai.
Pengelasan dan Sambungan: Pastikan pengelasan dan sambungan pada tangki dilakukan dengan hati-hati dan sesuai dengan standar keamanan. Lakukan pengujian non-destruktif untuk memastikan kualitas pengelasan dan sambungan.
Pengujian Kebocoran dan Tekanan: Lakukan pengujian tekanan dan kebocoran secara rutin untuk memastikan integritas tangki. Terapkan protokol pengujian yang ketat dan dokumentasikan hasil pengujian secara cermat.
Sistem Pelepas Tekanan Darurat: Pasang sistem pelepas tekanan darurat, seperti katup pelepas tekanan, yang akan berfungsi saat tekanan melebihi batas aman. Pastikan sistem tersebut dirancang dengan benar dan diuji secara teratur.
Pelatihan Operator dan Prosedur Keselamatan: Lakukan pelatihan operator yang komprehensif tentang penanganan, pengoperasian, dan pemeliharaan tangki hidrogen. Tetapkan prosedur keselamatan yang jelas dan pastikan operator memahaminya dengan baik.
Pemantauan dan Pemeliharaan Rutin: Lakukan pemantauan dan pemeliharaan rutin pada tangki hidrogen untuk mengidentifikasi masalah potensial sebelum terjadi kegagalan. Lakukan pemeriksaan dan pengujian secara berkala.
Perlu dicatat bahwa perancangan yang tepat dari tangki hidrogen membutuhkan pemahaman mendalam tentang teknologi dan keamanan tangki tekanan. Selalu berpegang pada standar dan regulasi yang berlaku, dan dapatkan bantuan dari ahli terkait jika diperlukan.
Geometrical Constraint
from math import pi
import pprint
'''
r = radius
circle_area = pi * r**2
circle_circumference = 2 * pi * r
h = height
cylinder_volume = pi * r**2 * h
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * h)
constraint for cylinder_volume be a constant of 1 liter (cubic centimeter)
cylinder_volume = 1000
h in terms of r
h = 1000/(pi * r**2)
substitute in
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
'''
mylist = [] # create a list of (surface area, radius)
for r in range(1, 21): # assume a maximum of 20cm radius
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
mylist.append((cylinder_surface, r))
# test
pprint.pprint(mylist)
r = 5
surface_list = []
while True:
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
surface_list.append((cylinder_surface, r))
r += 0.01
if r > 6:
break
print('minimum surface area and radius: ', min(surface_list))
min_surface = min(surface_list)[0]
sf = "Minimum surface of a 1000ml tank = {:0.2f} square centimeters"
print(sf.format(min_surface))
radius = min(surface_list)[1]
print("Radius of 1000ml tank = {:0.2f} centimeters".format(radius))
height = 1000/(pi * radius**2)
print("Height of 1000ml tank = {:0.2f} centimeters".format(height))
sf = "Ratio of height to radius of a minimized surface can = {:0.2f}"
print(sf.format(height/radius))
Using a purely cylindrical geometry for the storage tank is likely to be dangerous due to the existence of the corners on the ends, which present stress concentration regions or sites of failure. Most pressure vessels take on a curved shape on their ends to reduce stress concentration by using three geometries: hemispherical, ellipsoidal, and torispherical. Highest volume and surface area addition to lowest addition also goes in the same order. Therefore, since our goal is to minimize surface area while maintaining the same volume, it is most efficient to take on a torispherical end cap shape. The torispherical shape can be simplified as the cylindrical shape that has been given partial filleting. This filleting adjustment will reduce the overall volume of the structure, however. Therefore we need to adjust the geometrical parameters to compensate for the reduction from the filleting to create the end cap.
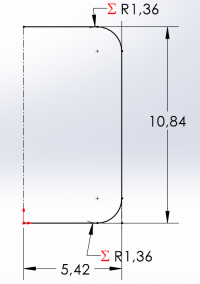
We can set a fillet of radius equal to half the radius of the container to create a smooth curvature for greater stress concentration reduction. An example sketch has been made via a computer-aided design program to visualize the reduction in cross-sectional area from the circumferential face. By law of proportionality, a percentage reduction in the cross sectional area would be equal to the same reduction in volume, therefore we can calculate the percentage reduction and apply inversely to our required volume to obtained the new increased volume constraint.
As shown, assuming a fillet radius of half the container radius, we have a new volume constraint of 1056.69 cubic centimeters to account for the percentage reduction in volume following formation of torispherical end caps through filleting. We can repeat the iteration process that was previously used to obtain new radius and height values for the cylinder. Upon iterating the first section of code, we find that the minimum surface area occurs between values of 5 and 6 cm radii again, therefore the upper and lower bounds of the second set of code do not need to be adjusted. The final results as as follows:
minimum surface area and radius: (574.3098652360588, 5.519999999999989)
Minimum surface of a 1056.69ml tank = 574.31 square centimeters
Radius of 1056.69ml tank = 5.52 centimeters
Height of 1056.69ml tank = 10.45 centimeters
Ratio of height to radius of a minimized surface can = 1.89Material Strength Constraint
The constraints for this assumption to be true is that the radius must be at least 5 times the wall thickness, which we will verify later. The stresses that exist within a thin-wall cylindrical component are circumferential (hoop) stress and longitudinal stress. Radial stress also exists but can be neglected due to the radius being much greater than the wall thickness. Hoop stress and longitudinal stress can be obtained via the following formulae:
where p is the gage pressure of the fluid and t is the wall thickness.
Since the hoop stress is equal to twice the longitudinal stress, we can set it as the objective function over the latter since quantitatively failure will occur earlier due to the hoop stress instead of the longitudinal stress. Since we have already calculated the container radius previously, have the pressure constraint set at 8 bars of gage pressure from the hydrogen, we can numerically iterate for the thickness of the vessel to obtain a range of values of hoop stresses. From there, we can select thicknesses with corresponding hoop stresses that do not exceed allowable stress of the material, in this case we arbitrarily set at 0.875 of the yield strength of the material. In containment purposes such as these, deformations in the container can already be considered failure or at least compromising for the storage facility, hence the consideration for setting the constraint at the yield strength.
Literary Parameters
The range of wall thickness that is applicable is also not arbitrary outside of remaining less than one-fifth of the vessel radius. ASME BPV Code Section VIII D.1 states that wall thickness should always be at least 1/16 in (1.59 mm), not considering corrosion allowance, material, or dimensions. Literary source "Analysis, Synthesis, and Design of Chemical Processes" gives heuristics for wall thickness for rigidity based on vessel diameter: 4 mm (0.25 in) for 1.07 m (42 in) diameter and less than 8.1mm (0.32 in) for 1.07-1.52 m (42-60 in) diameter, and 11.7 mm (0.38 mm) for more than 1.52 m (60 in) diameter (Turton et al., 2012). Taking a conservative approach of setting the minimum thickness to be in between 1.59mm and 4mm, thereby 2.8mm, we will begin the iteration of the thickness from 2.80mm up to 11.04mm at increments of 0.01mm for precision.
Based on data obtained from Ferrobend, a typical workpiece of AISI 316 stainless steel has the mechanical properties as shown. For the purpose of our testing, we will utilize both a conservative and less conservative method by setting our limit at the yield strength as well as the maximum tensile strength to signify failure.
Iteration Process
We can use a simple code to numerically iterate the possible thickness and hoop stress values:
r = 5.52e-2
p = 800000
t = 2.8e-3
while t < 11e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 0.1e-3
if hoop > 205e9:
breakFrom the above code we obtain hoop stress values for each iterated thickness values from 2.8 mm to 11 mm. A further constraint was placed in the final lines where the looping would stop if the total hoop stress exceeded the yield strength of the material (stainless steel AISI 316).
From the results, all possible thickness values from 2.8mm to 11mm on 0.1mm increments remain within the yield strength constraint, therefore are all applicable. Shown below are the results from the code for thickness range 4 mm to 7 mm, with hoop stress values ranging below 10 MPa, which is less than 5% of the yield strength limit.
for thickness 0.004099999999999999 hoop stress = 10770731.707317077 Pa
for thickness 0.004199999999999999 hoop stress = 10514285.714285716 Pa
for thickness 0.004299999999999999 hoop stress = 10269767.441860467 Pa
for thickness 0.004399999999999999 hoop stress = 10036363.636363639 Pa
for thickness 0.0045 hoop stress = 9813333.333333334 Pa
for thickness 0.0046 hoop stress = 9600000.0 Pa
for thickness 0.0047 hoop stress = 9395744.680851063 Pa
for thickness 0.0048000000000000004 hoop stress = 9200000.0 Pa
for thickness 0.004900000000000001 hoop stress = 9012244.897959182 Pa
for thickness 0.005000000000000001 hoop stress = 8831999.999999998 Pa
for thickness 0.005100000000000001 hoop stress = 8658823.529411763 Pa
for thickness 0.0052000000000000015 hoop stress = 8492307.69230769 Pa
for thickness 0.005300000000000002 hoop stress = 8332075.47169811 Pa
for thickness 0.005400000000000002 hoop stress = 8177777.777777774 Pa
for thickness 0.005500000000000002 hoop stress = 8029090.909090905 Pa
for thickness 0.0056000000000000025 hoop stress = 7885714.285714282 Pa
for thickness 0.005700000000000003 hoop stress = 7747368.421052628 Pa
for thickness 0.005800000000000003 hoop stress = 7613793.103448272 Pa
for thickness 0.005900000000000003 hoop stress = 7484745.76271186 Pa
for thickness 0.006000000000000004 hoop stress = 7359999.999999995 Pa
for thickness 0.006100000000000004 hoop stress = 7239344.262295078 Pa
for thickness 0.006200000000000004 hoop stress = 7122580.645161286 Pa
for thickness 0.006300000000000004 hoop stress = 7009523.809523805 Pa
for thickness 0.006400000000000005 hoop stress = 6899999.999999995 Pa
for thickness 0.006500000000000005 hoop stress = 6793846.153846148 Pa
for thickness 0.006600000000000005 hoop stress = 6690909.090909085 Pa
for thickness 0.006700000000000005 hoop stress = 6591044.776119398 Pa
for thickness 0.006800000000000006 hoop stress = 6494117.6470588185 Pa
for thickness 0.006900000000000006 hoop stress = 6399999.999999994 Pa
for thickness 0.007000000000000006 hoop stress = 6308571.428571423 Pa
Cost Constraints
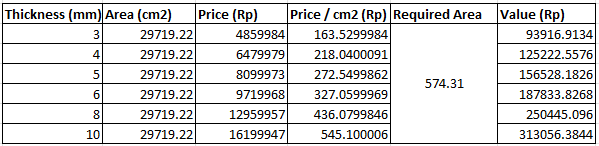
With the geometrical parameters available, we need to compare with the cost constraint that was provided which is that the total cost for materials used should not exceed Rp500.000,-. Therefore, from the material that has been previously considered, we must select the thickness which remain within the cost range. As this is a small-size thin-walled vessel, the most likely method of manufacture is through sheet-metal manufacturing like those used to manufacture storage and beverage cans. Therefore, material purchase would be done in the sheet-metal or plate form.
In the table above, the selection of thickness ranges have been minimized to only include those within our region of interest. Since steel plates are rarely distributed at small surface areas such as the one in our application, a cost per area analysis approach is used based on the data obtained from PT Citra Anggun Lestari. Similar to the circumstances encountered in the strength constraint, all possible thickness values result in material costs that are lower than our set cost constraint. Therefore to select the thickness that we will use, we will also consider the need to minimize the weight and maintain a reasonable amount of strength, which suggests the selection of the median 6 mm wall thickness for the container.
To optimize the storage of hydrogen at 8 bar pressure with a 1-liter capacity and a maximum budget of Rp500,000, we can approach it as an optimization problem by using a phyton's code below:
from scipy.optimize import minimize
# Price and capacity
price_per_unit = 100000 # Price per unit of hydrogen storage
capacity_per_unit = 1 # Capacity of hydrogen storage per unit
# Maximum budget
max_budget = 500000
# Objective function
def objective_function(x):
return -x * capacity_per_unit
# Constraint function
def budget_constraint(purchase_amount):
return max_budget - (price_per_unit * purchase_amount)
budget_constraint_eq = {'type': 'ineq', 'fun': budget_constraint}
# Initial value
x0 = 0
# Bounds
bounds = [(0, None)]
# Solve the optimization problem
solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=[budget_constraint_eq])
# Print the results
print("Status:", "Optimal" if solution.success else "No solution found")
print("Number of hydrogen storage units to be purchased:", solution.x[0])
print("Total storage capacity:", solution.x[0] * capacity_per_unit, "liters")
print("Total cost:", solution.x[0] * price_per_unit, "Rupiah")This code will calculate the optimal number of hydrogen storage units to be purchased within the given budget, considering a storage capacity of 1 liter per unit and a price per unit of Rp100,000. The optimization problem is solved using the SLSQP method, and the results are printed, including the status, the number of units to be purchased, the total storage capacity, and the total cost in Rupiah.
From the code above, we obtain the following information:
Status: Optimal Number of hydrogen storage units to be purchased: 5.0 Total storage capacity: 5.0 liters Total cost: 500000.0 Rupiah
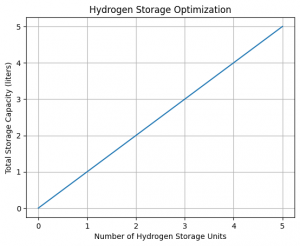
We can also use phyton to show graphic between total storage and hydrogen storage optimazation:
import matplotlib.pyplot as plt
# Price and capacity
unit_price = 100000 # Price per unit of hydrogen storage
unit_capacity = 1 # Capacity per unit of hydrogen storage
# Maximum budget
max_budget = 500000
# Initialize variables
best_unit_count = 0
best_total_capacity = 0
best_total_cost = 0
# Initialize lists for the graph
unit_count_list = []
total_capacity_list = []
# Iteration to find the optimal solution
for unit_count in range(int(max_budget / unit_price) + 1):
total_capacity = unit_count * unit_capacity
total_cost = unit_count * unit_price
if total_capacity > best_total_capacity and total_cost <= max_budget:
best_unit_count = unit_count
best_total_capacity = total_capacity
best_total_cost = total_cost
# Add data to the lists for the graph
unit_count_list.append(unit_count)
total_capacity_list.append(total_capacity)
# Display the results
print("Number of hydrogen storage units to be purchased:", best_unit_count)
print("Total storage capacity:", best_total_capacity, "liters")
print("Total cost:", best_total_cost, "Rupiah")
# Display the graph
plt.plot(unit_count_list, total_capacity_list)
plt.xlabel('Number of Hydrogen Storage Units')
plt.ylabel('Total Storage Capacity (liters)')
plt.title('Hydrogen Storage Optimization')
plt.grid(True)
plt.show()This code calculates the optimal number of hydrogen storage units to be purchased based on the given price per unit, capacity per unit, and maximum budget. It iterates through the possible number of units within the budget and calculates the corresponding total storage capacity and cost. It keeps track of the best solution with the highest total capacity while staying within the budget. The results are then printed, including the number of units, total capacity, and total cost. Additionally, the code plots a graph showing the relationship between the number of units and the total storage capacity.