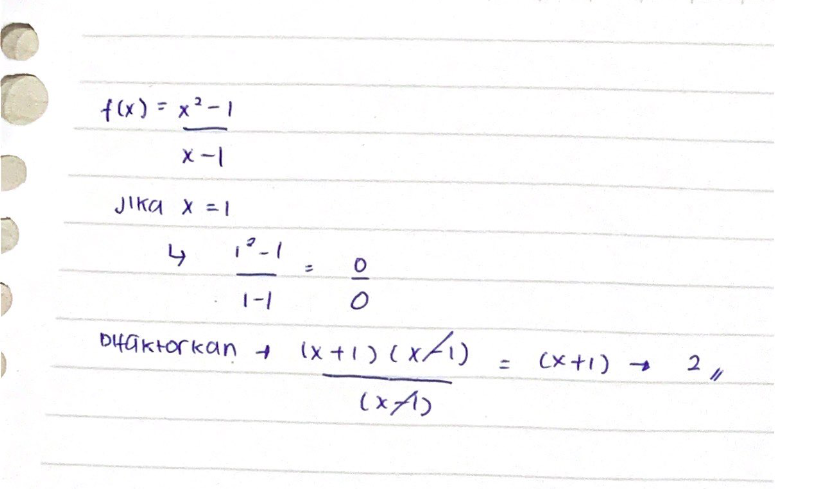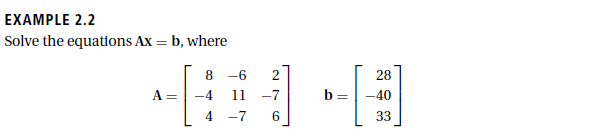Muhammad Raihan Haidar

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

Data Diri

Nama : Muhammad Raihan Haidar

NPM : 1606886204

Mahasiswa Departemen Teknik Mesin 2016 Jurusan Teknik Perkapalan

Pertemuan Pertama Metode Numerik

Hari, Tanggal : Jumat, 7 Februari 2020

Oleh : Dr. Ahmad Indra & Prof. Dr. Ir. Harinaldi M.Eng.

Pada Pertemuan Pertama ini saya di perkenalkan dengan air.eng.ui.ac.id untuk berdiskusi dan mengumpulkan tugas yang diberikan. Alhamdulillah dengan belajar pemrograman nanti nya insyaallah saya dapat mengolah data dengan lebih baik.

Tugas Pengalaman Coding

Perkenalkan nama Saya Muhammad Raihan Haidar, Saya biasa dipanggil Ihan. Saya lahir di Bekasi tanggal 14 Maret 1998. 

Pengalaman Saya dengan Pemrograman terutama Coding itu saat saya Praktikum, ketika mengolah data menggunakan excel dan membuat 
grafik dari data-data tersebut. Selain itu saya juga banyak menggunakan coding di Mata Kuliah Tugas Merancang Kapal (TMK) saat 
semester 4, 5 dan 6. Pada mata kuliah TMK sangat diperlukan kemampuan coding dan pemrograman karena sangat banyak pengolahan data 
dan pembuatan grafik.

Tugas Pertama Metode Numerik

Soal
T(x)= (x^2-1)/(x-1)

Pada proses Pertama, saya mencoba menyelesaikan persamaan dengan cara manual yaitu dengan memfaktorkan persamaan kemudian memasukan x sebesar 1.

Saya memakai Bahasa python dengan menggunakan software bernama spyder. Di dalam metode ini saya mendefinisikan fungsi yang dicari. Selain itu saya juga menginput x, jadi codingan di metode Pertama ini dapat menyesuaikan Nilai x selain 1.

Algoritma yang saya gunakan pada metode pertama adalah

def h(x):
    return (x**2-1)/(x-1)
def f(x):
    return(x+1)
x =input ('insert x')
z =int(x)
if z==1: print (f(z))
else : print(h(z))

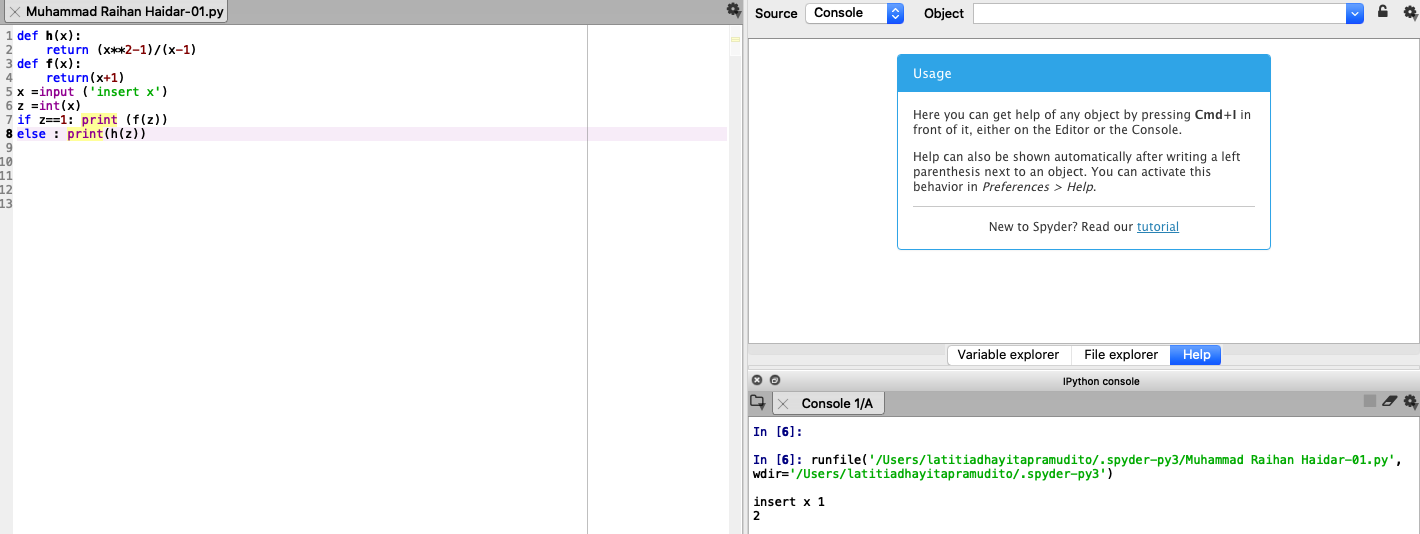
Hasil dari melakukan run pada algoritma diatas adalah :

2

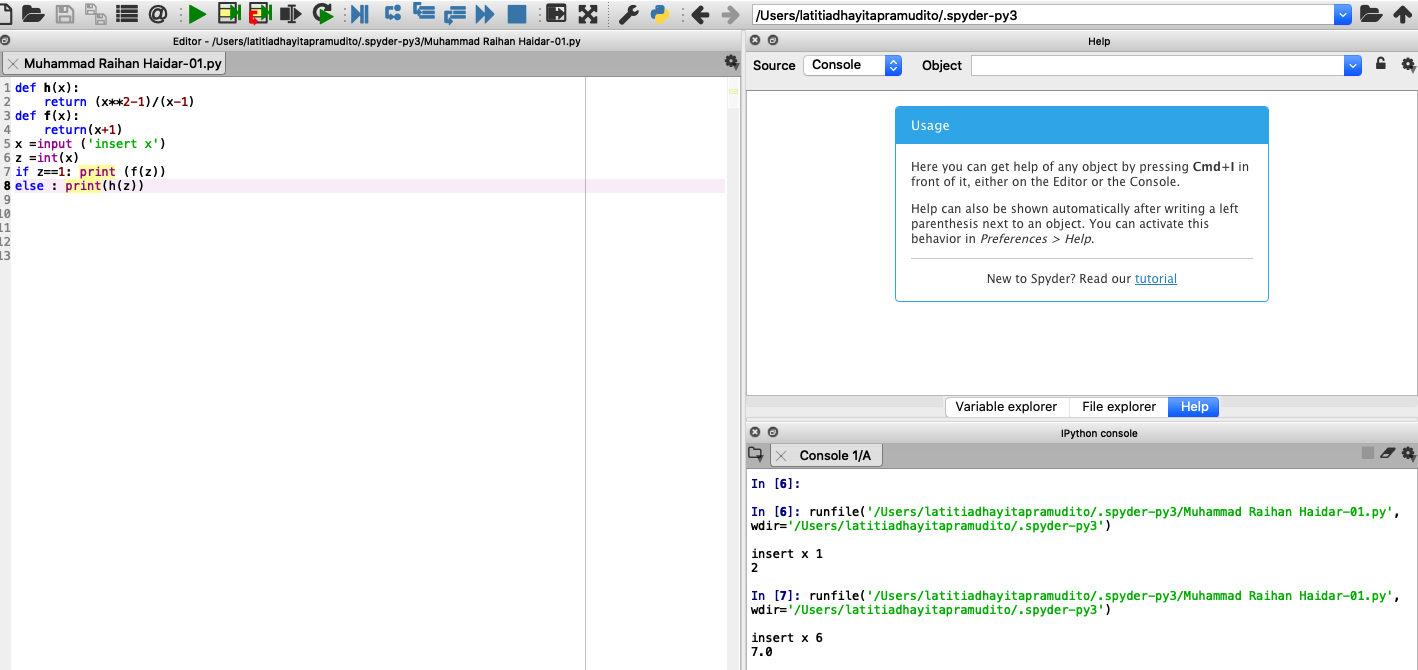
Pada foto dibawah ini saya mencoba menggunakan x sebesar 6, Hasil yang didapatkan adalah sebesar 7

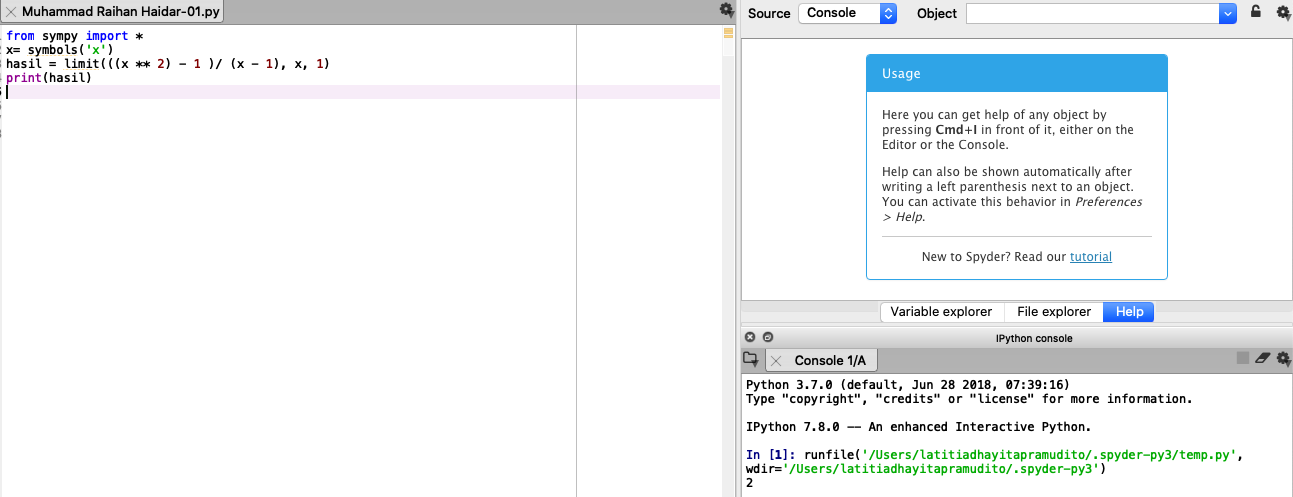
Algoritma yang saya gunakan pada metode dua adalah menggunakan modul sympy

from sympy import *
x= symbols('x')
hasil = limit(((x ** 2) - 1 )/ (x - 1), x, 1)
print(hasil)

Hasil yang didapatkan setelah melakukan run pada algoritma diatas adalah :

2

Dari perhitungan menggunakan 2 metode yaitu manual dan phyton (modul dan definisi) didapatkan bahwa untuk menyelesaikan persamaan lebih mudah menggunakan metode Phyton karena dengan membuat satu codingan dapat memvariasikan nilai variabel x

Pertemuan Kedua Metode Numerik

Hari, Tanggal : Jumat, 14 Februari 2020

Oleh : Dr. Ahmad Indra & Prof. Dr. Ir. Harinaldi M.Eng.

Pada pertemuan kali ini diajarkan untuk menggunakan bahasa phyton untuk menyelesaikan masalah-masalah di matakuliah khususnya dalam hitungan seperti menghitung percepatan pada buah kelapa yang jatuh, ataupun menyelesaikan soal aljabar linear. Hari ini juga kembali mereview materi pertemuan sebelumnya agar mahasiswa tetap selalu ingat materi pada setiap pertemuan. Motivasi agar terus semangat dalam belajar adalah dengan mendorong diri untuk bertanggung jawab pada Allah SWT.

Tugas Kedua Metode Numerik

Bagian A (Aljabar Linear)

Mengambil soal dari buku :

Hasil Perhitungan Menggunakan Manual :

Hasil Perhitungan Menggunakan Bantuan Bahasa Python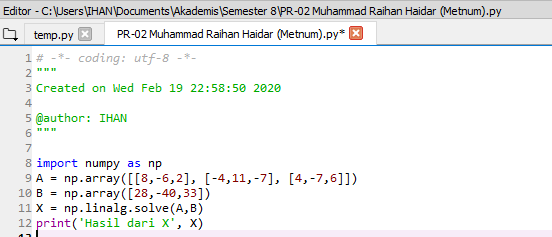

Didapatkan hasil sebesar :


Coding yang digunakan :
import numpy as np
A = np.array([[8,-6,2), [-4,11,-7], [4,-7,6]])
B = np.array([28,-40,33])
X = np.linalg.solve(A,B)
print('Hasil dari X', X)

Dari perhitungan soal matriks aljabar linear diatas didapatkan dengan metode manual dan metode bahasa phyton memiliki hasil yang sama. Namun dalam pengerjaannya jelas lebih mudah menggunakan metode bahasa phyton karena lebih ringkas dan cepat serta juga dapat menghindari kesalahan-kesalahan hitung yang biasa disebut human error.

Bagian B (Initial Value Problem)

Dengan menggunakan soal gerak jatuh bebas pada sebuah buah kelapa

Hasil Perhitungan Manual :
 

Hasil Perhitungan Menggunakan Bantuan Bahasa Python :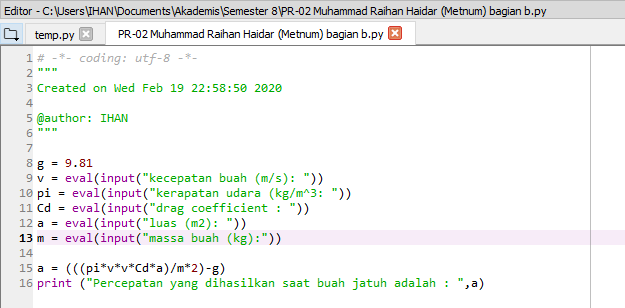

Didapatkan hasil sebesar :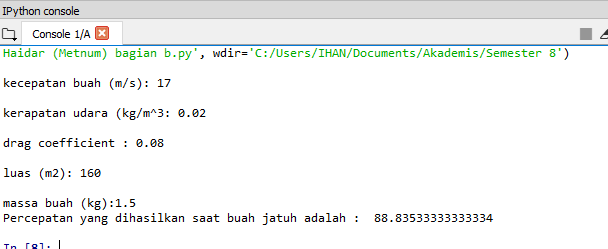

Coding yang digunakan :
g = 9.81
v = eval(input("kecepatan buah (m/s): "))
pi = eval(input("kerapatan udara (kg/m^3: "))
Cd = eval(input("drag coefficient : "))
a = eval(input("luas (m2): "))
m = eval(input("massa buah (kg):"))

a = (((pi*v*v*Cd*a)/m*2)-g)
print ("Percepatan yang dihasilkan saat buah jatuh adalah : ",a)

Saya menggunakan metode eval(input() agar codingan ini dapat digunakan untuk soal lain yang memiliki identifikasi besaran yang berbeda.

Dari perhitungan soal Initial Value Problem dengan metode manual dan metode bahasa phyton diatas didapatkan hasil yang sama. Namun sangat lebih mudah menggunakan metode bahasa phyton karena memperingkas pekerjaan dan terhindar dari human error.

Progress Belajar 1

Laporan Asistensi

Tugas 3

Laporan Asistensi 2

Tugas 4

Langkah pertama kita upload data kapal ke CFDSOF

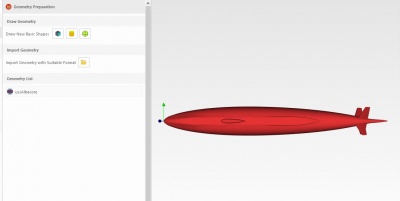
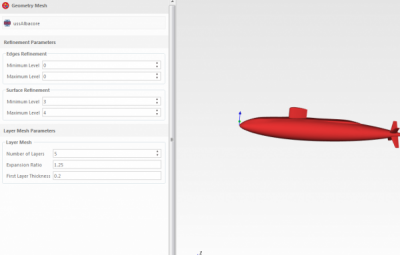
Langkah kedua yaitu ubah data Geometry Mesh

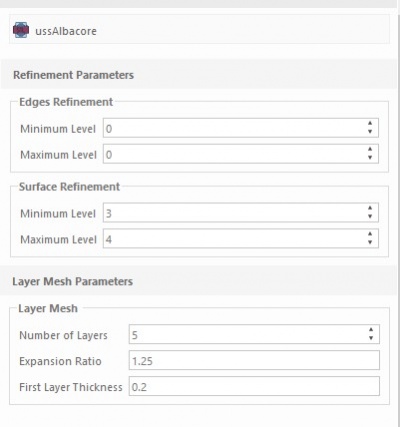
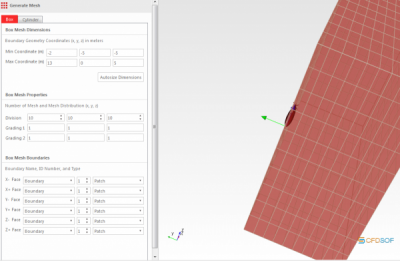
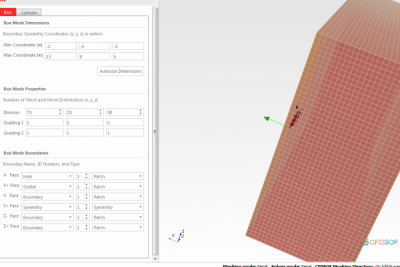
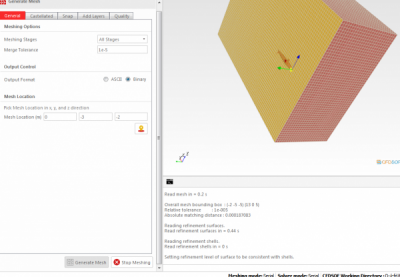
Selanjutnya kita ubah data Base Mesh dan Generate Mesh.

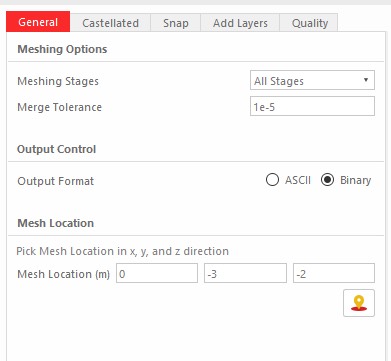
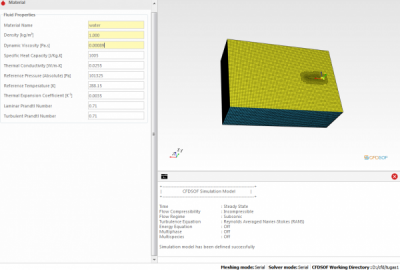
Setelah itu mengubah Data Simulation dan Data Water di fluid properties

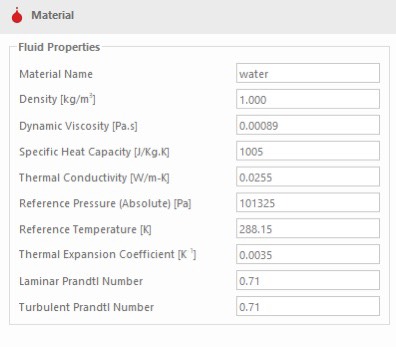
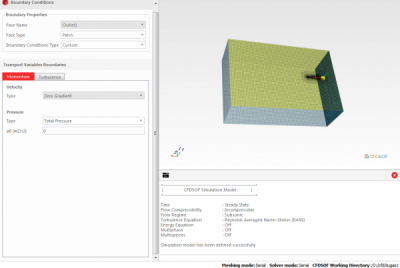
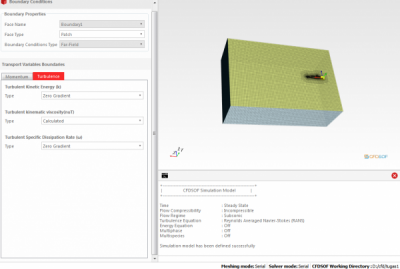
Selanjutnya kita tinggal mengubah Boundary condition dan kita tinggal Run Solver

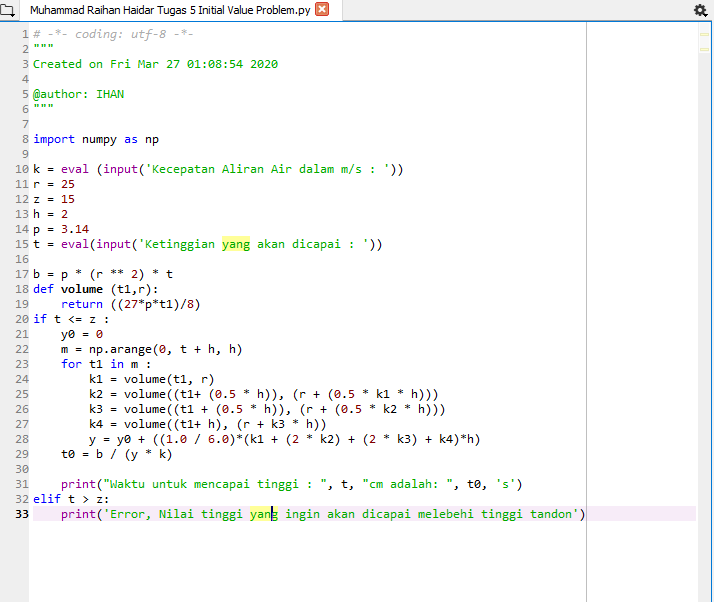
Tugas 5 Iniitial Value Problem

Tugas kali ini diminta untuk menyelesaikan permasalahan sehari-hari dengan initial value problem.

Jadi saya ingin menyelesaikan sebuah kasus yaitu mencari waktu yang dibutuhkan untuk mengisi Tandon Air pada ketinggian tertentu.

Pada awalnya saya misalkan jika jari-jari Tandon nya adalah 25 dan tinggi nya adalah 15 yang diisi air dengan kecepatan tertentu.

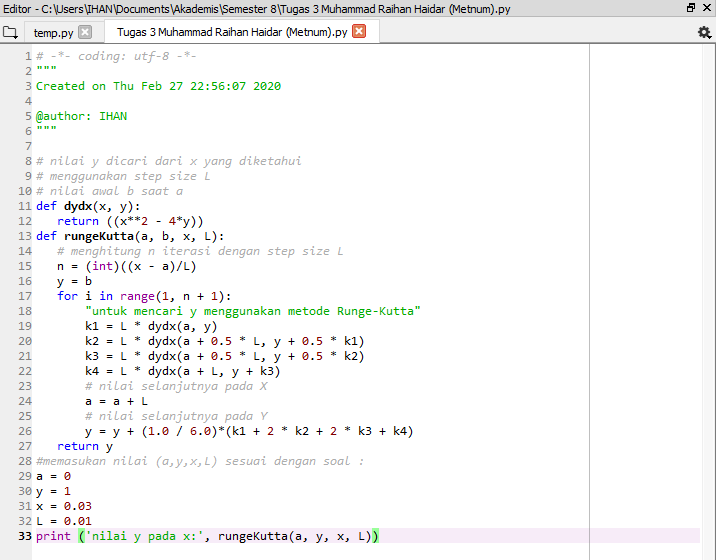
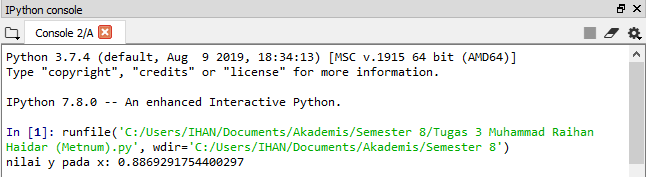
Kemudian dilakukan programming dengan metode runge kutta, kita ditanyakan kecepatan aliran dan ketinggian yang akan dicapai.

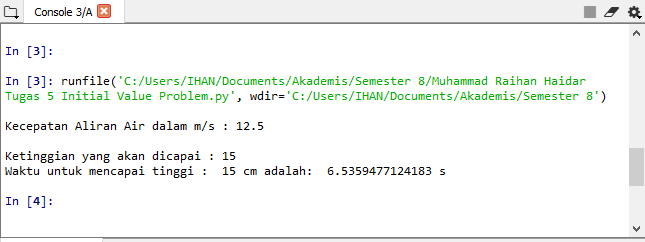
saya memasukan kecepatan aliran nya 12.5 m/s dan ketinggian 15. didapatkan hasil sebagai berikut.

ANALISIS dan KOMENTAR

Initial Value Problem ini merupakan sebuah permasalahan yang sudah diketahui permasalahan awalnya dah sudah diketahui indikator-indikator pengaruhnya sehingga proses penyelesaiannya dapat menggunakan metode Runge Kutta yang diprogram dalam Phyton.

Tugas 5 Boundary Value Problem

Persoalan yang saya ambil adalah drag force pada saat mobil berjalan. 

Pertama saya mengambil CAD mobil dari yang sudah disediakan. Lalu saya memmasukan CAD kedalam aplikasi CFD untuk melihat Drag Force dengan variasi kecepatan. Untuk membantu saya,  saya menggunakan CFDSOF untuk menghitung hal ini. Awalnya saya menentukan besaran mesh yang kita butuhkan, yang saya ambil pada saat mesh berada di tengah mobil untuk melihat besaran  Drag Forcenya. Jadi diasumsikan aliran yang melewati mobil bagian paling teratas. 

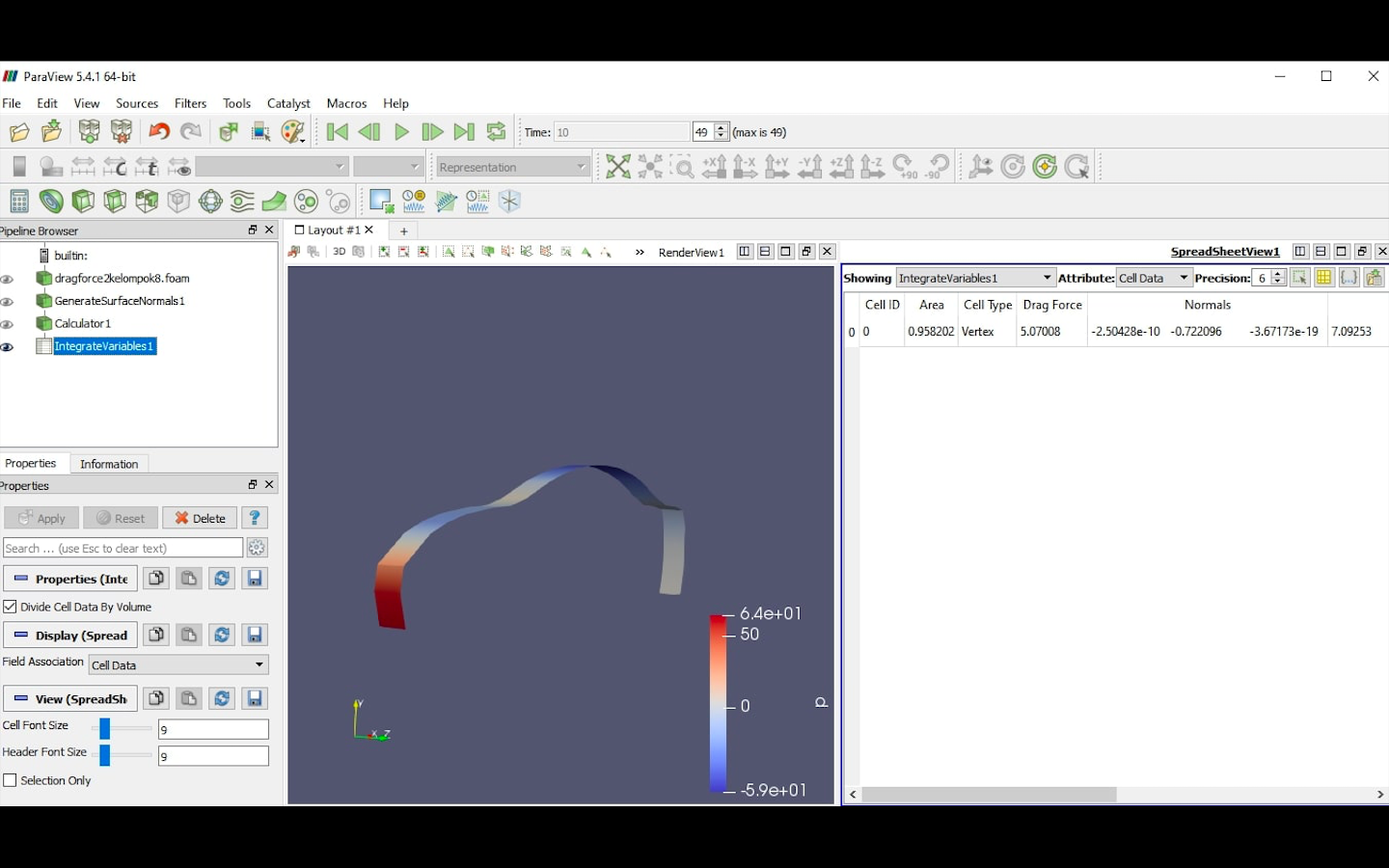
Setelah menentukan mesh, saya berlanjut melakukan perhitungan pada aplikasi Paraview yang menjadi third party dari CFDSOF. Pada applikasi ini, saya dapat menghitung Drag Force  menggunakan calculator yaitu dengan mengalikan p*Surface x. 

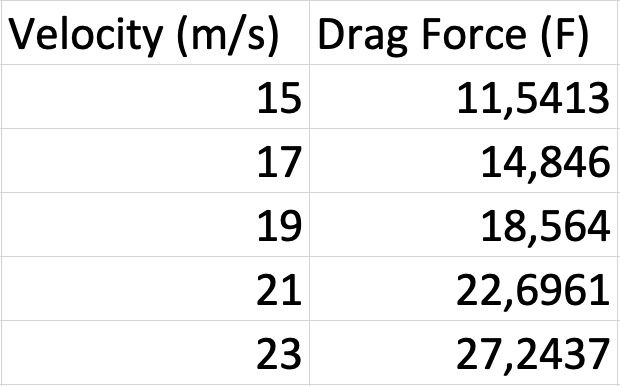
Setelah saya melakukan percobaan dengan variasi sebanyak 5 kecepatan didapat 5 macam data sebagai berikut :

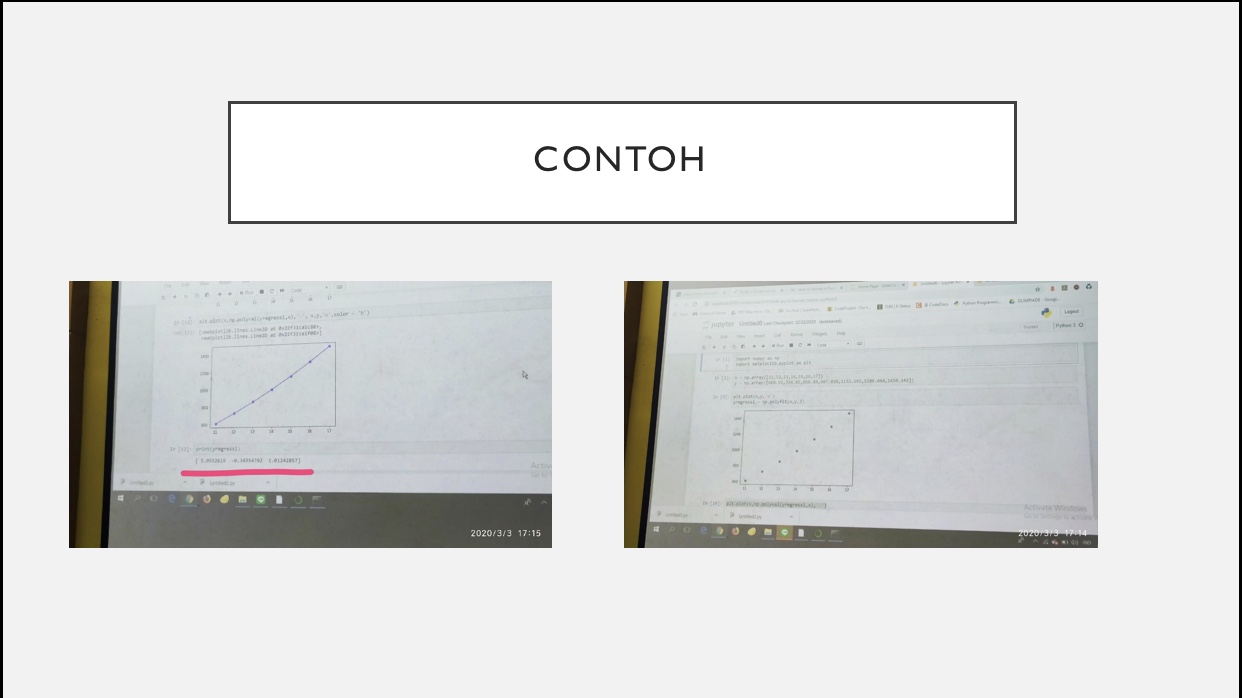
Setelah itu Saya melakukan regresi linear untuk mendapatkan hasil curve fittingnya menggunakan cara :

Laporan Asistensi 3

Tugas PERTEMUAN KE-6

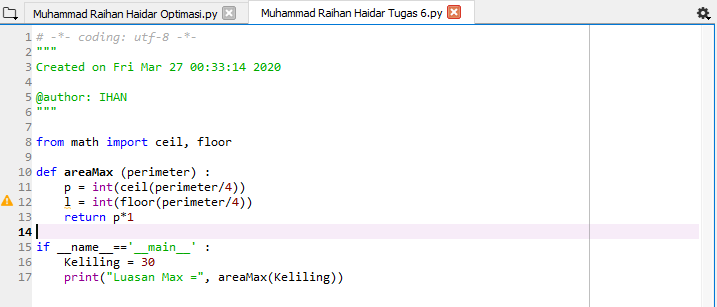
Jadi pertemuan kali ini di ajarkan oleh asisten dosen dan diberikan tugs, berikut tugas milik saya:

ini codding menggunakan PHYTON

ini hasil nya

Tugas Simulasi CFDSOF

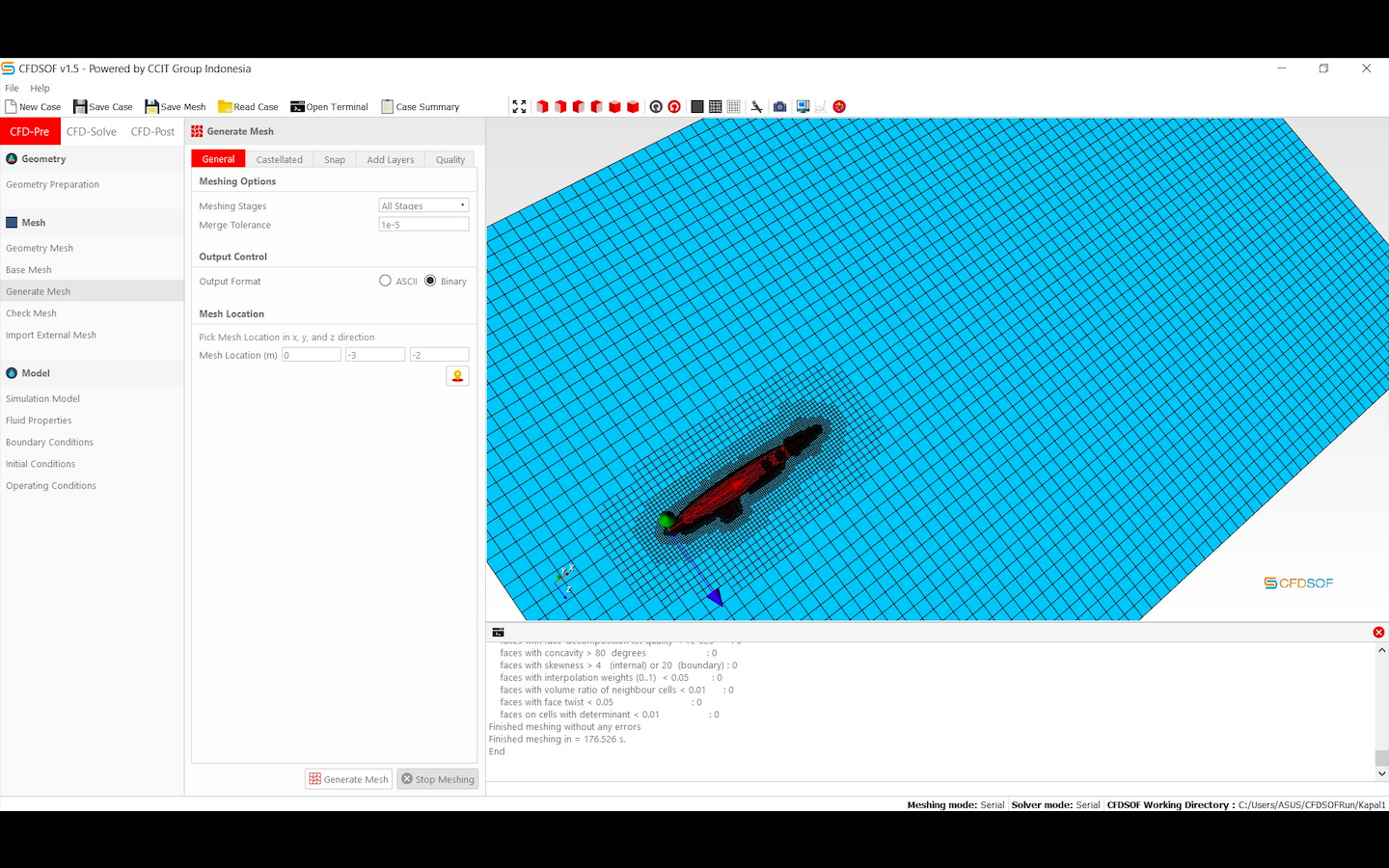
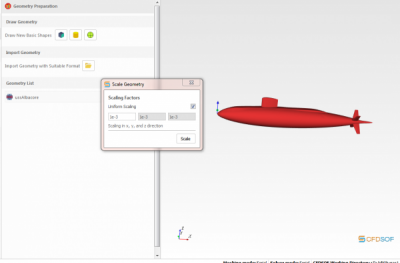
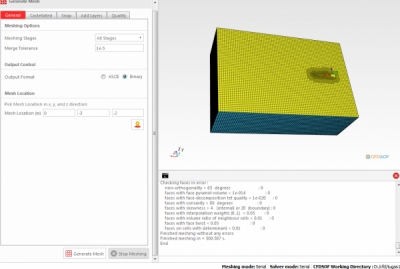
Pada tugas ini, saya mengerjakan Permodelan kapal selam yaitu USS albacore menggunakan CFDSOF. Permodelan ini dilakukan untuk dapat melakukan perhitungan regresi dengan mendapatkan data-data kecepatan. Berikut ini merupakan langkah-langkah permodelan yang dilakukan.

400px

Pada langkah berikutnya dapat dilakukan variasi memasukan kecepatan. Kecepatan yang akan saya masukkan adalah 11,12,13,14,15,16,17,18,19,20

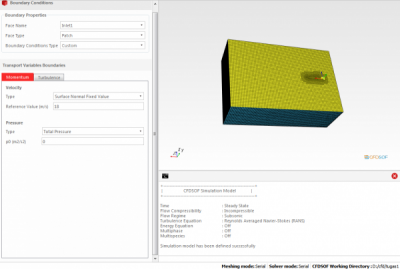
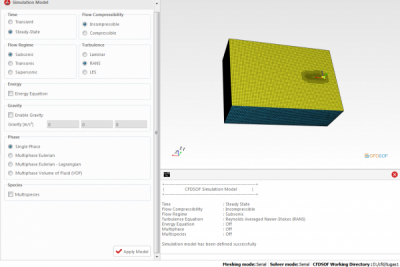
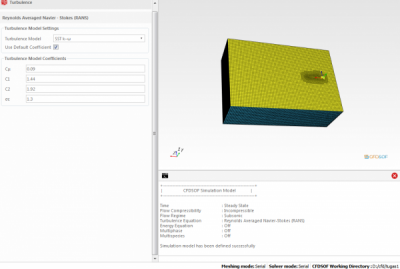
Langkah berikutnya adalah menentukan kondisi otlet dan boundary

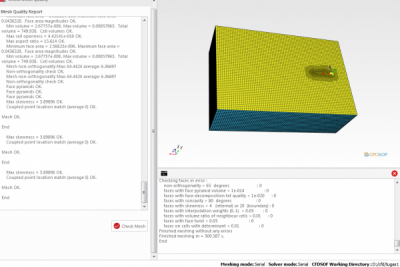
Langkah terakhir adalah melakukan pengecekan dan melihat hasil pada aplikasi pihak ketiga Paraview. Langkah ini dilakukan untuk mendapat hasil dari semua variabel keceapatan.

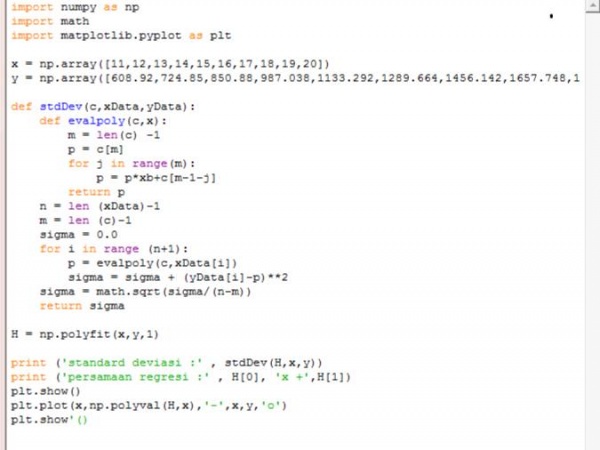
Data yang saya dapatkan berturut-turut dari kecepatan 11 m/s hingga 20 m/s - 608.92 - 724.85 - 850.88 - 987.038 - 1133.292 - 1289.664 - 1456.142 - 1657.748 - 1847.352 - 2047.18

penyelasaian secara regresinya

Video Optimasi

UTS

Berikut ini adalah link Video Simulasi AUV dengan CFDSOFT dan Phyton Video UTS Muhammad Raihan Haidar di Youtube