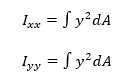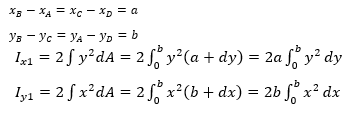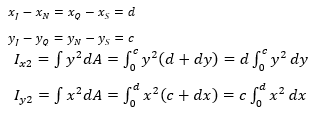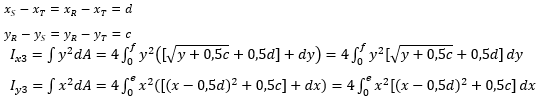Momen Inersia

MOMEN INERSIA SEMBARANG BENTUK

Momen inersia (Satuan SI : kg m2) adalah ukuran kelembaman suatu benda untuk berotasi terhadap porosnya. Besaran ini adalah analog rotasi dari pada massa. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalar terhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik. Lambang dan kadang-kadang juga biasanya digunakan untuk merujuk kepada momen inersia. Konsep ini diperkenalkan oleh Euler dalam bukunya a Theoria motus corporum solidorum seu rigidorum pada tahun 1730.

Untuk mencari nilai inersia sebuah penampang, biasanya lebih sering menggunakan cara langsung dengan menggunakan integral atau menggunakan tabel jika bentuknya regular. Bentuk umum untuk menentukan nilai momen inersia diberikan dalam bentuk integrasi berikut:

Namun untuk bentuk polinomial, bentuk integral di atas sangat susah dikerjakan, apalagi jika menggunakan hitungan manual dengan tangan, pasti akan lama mendapatkan nilainya. Dengan bantuan komputer dan analisis metode numerik, momen inersia berbagai bentuk bisa dicari.

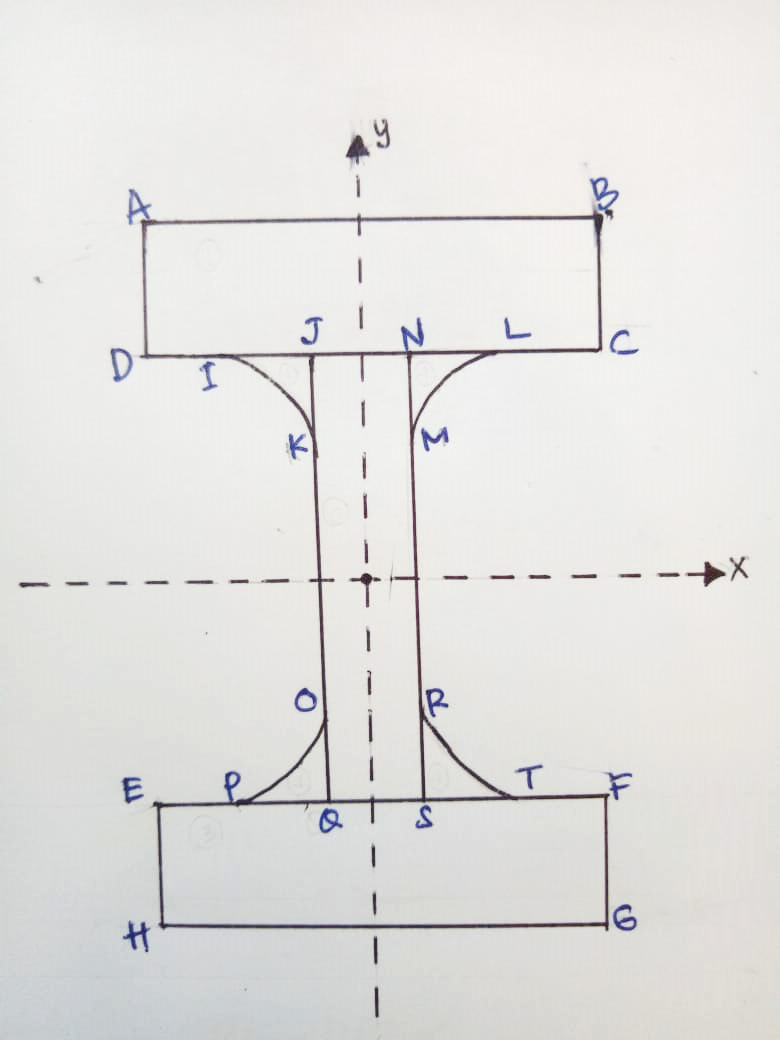
Pada persoalan kali ini dilakukan analisa perhitungan momen inersia yang terjadi pada bentuk sembarang seperti gambar di bawah ini :

Gambar 1. Penampanang balok kolom pada bidang x-y

Dilakukan perhitungan inersia ke arah x (Ix) dan inersia ke arah y (Iy) untuk sebuah permukaan benda dari gambar di atas. Untuk mencari inersia tersebut, benda dibagi menjadi beberapa bagian. Hal tersebut dikarenakan inersia bersifat skalar sehingga hasil dapat dihitung dengan artimatika biasa. Berdasarkan gambar tersebut maka dilakukan pembagian bentuk agar memudahkan menghitung momen inersianya sebagai berikut :

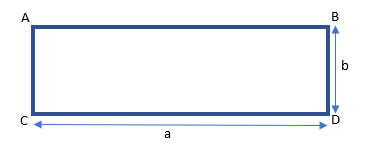
1. Persegi panjang horizontal

Gambar 2. Penampang bagian 1 pada balok ABCD

Bagian 1 memiliki bentuk persegi panjang dengan luas a x b. Selain balok ABCD, balok yang juga merupakan bagian I adalah balok EFGH. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 1 adalah:

2. Persegi panjang vertical

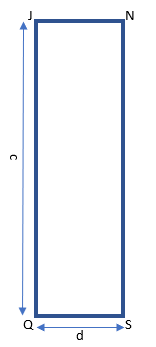
Gambar 3. Penampang bagian 2 pada balok JNQS

Bagian 2 memiliki bentuk persegi panjang dengan luas c x d. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 2 adalah:

3. Seperempat lingkaran

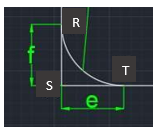
Gambar 4. Penampang bagian 3 pada balok RST

Bagian 3 memiliki bentuk berupa fungsi f(x) = (x-0.5d)2 - 0.5c dari titik xS ke xT dan yR ke yS. Selain balok RST, balok yang juga merupakan bagian 3 adalah balok OPQ, IJK dan LMN. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 3 adalah:

Dari penjabaran rumus inersia tersebut maka dilakukan pengerjaan contoh soal sebagai berikut :

Diketahui:

- a = 20 cm = 0.2 m

- b = 5 cm = 0.05 m

- c = 16 cm = 0.16 m

- d = 7 cm = 0.07 m

- e = f = 3.2 cm = 0.032 m

- f(x)RST, OPQ, IJK, LMN = (x – 3)2 – 7

Ditanya: Ix dan Iy balok kolom?

Dijawab:

Flowchart pengerjaan :

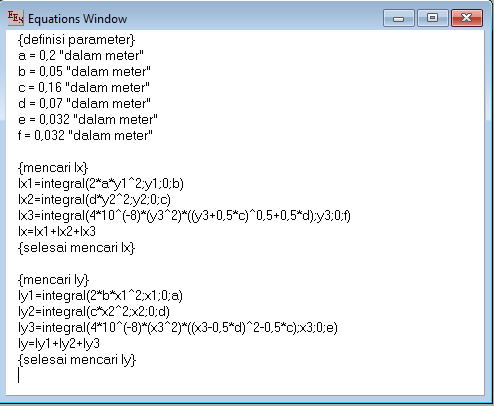
Setelah dilakukan perumuman di atas, maka dilakukan pemodelan yang akan diselesaikan dengan menggunakan EES sebagai berikut :

Gambar 5. Proses input data

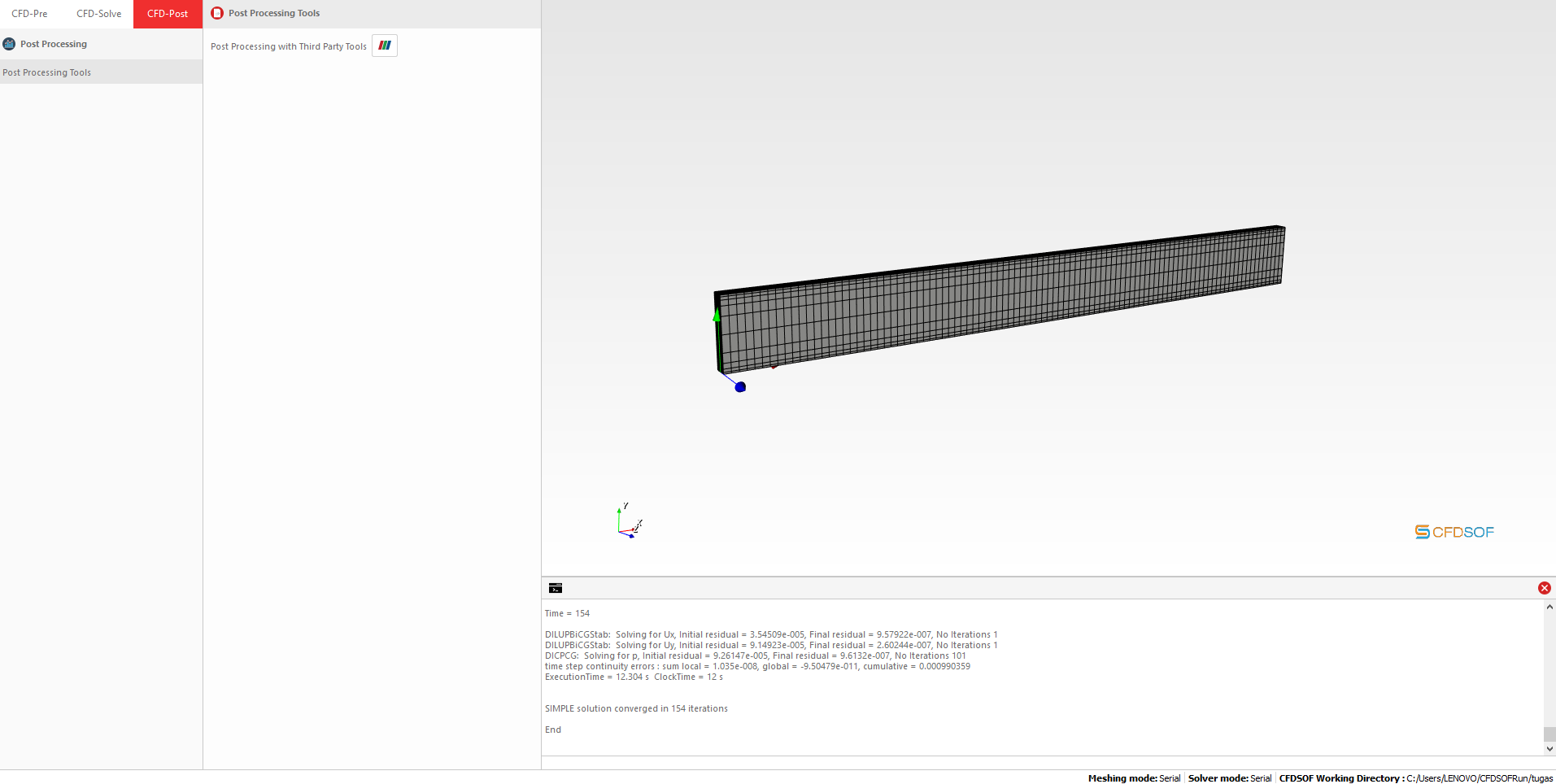
Gambar 6. Proses running data

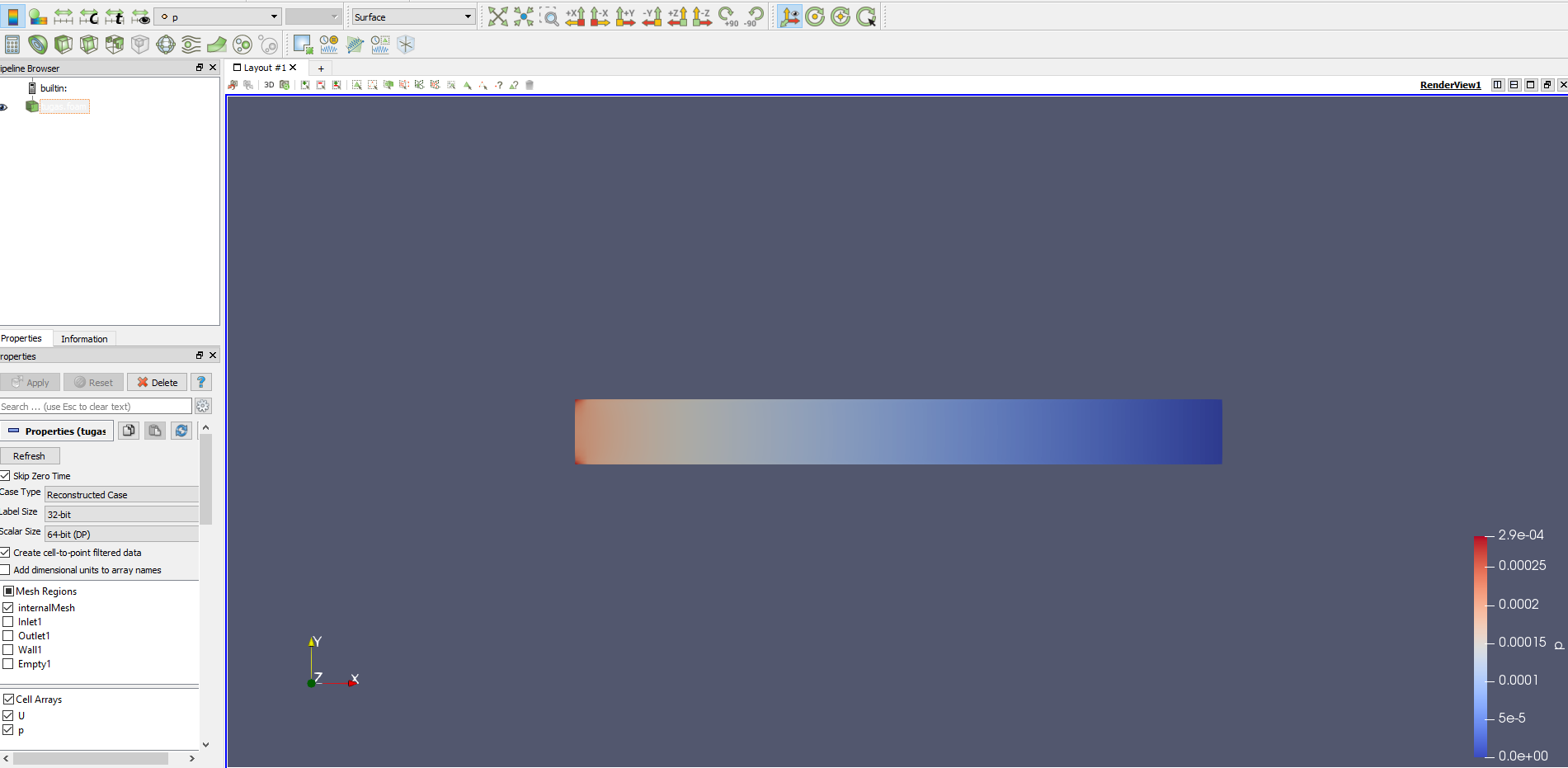
Hasil dari running data tersebut adalah sebagai berikut :

Gambar 7. Hasil running

Berdasarkan hasil iterasi yang diperoleh dari EES, didapat hasil sebagai berikut :

Ix = 1,122 x 10-4 m4

Iy = 2,85 x 10-4 m4