Mochamad Farhan Zidny
Contents
[hide]- 1 profil
- 2 Pertemuan 1 (3 September 2019)
- 3 Pertemuan 2 (10 September 2019)
- 4 Pertemuan 3 (17 September 2019)
- 5 Pertemuan 4 (24 September 2019)
- 6 Pertemuan 5 (1 Oktober 2019)
- 7 Pertemuan 6 dan Tugas 1 (29 Oktober 2019)
- 8 Pertemuan 7 (5 November 2019)
- 9 Pertemuan 8 (12 November 2019)
- 10 Pertemuan 9 (19 November 2019)
- 11 Pertemuan 10 (26 November 2019)
- 12 Pertemuan 11 (3 Desember 2019)
- 13 Pertemuan 12 (10 Desember 2019)
profil
- Nama : Mochamad Farhan Zidny
- NPM : 1706986391
- Prodi: Teknik Mesin
Progress Tugas Merancang - Mochamad Farhan Zidny
Pertemuan 1 (3 September 2019)
Metode Numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematika sehingga dapat dipecahkan dengan operasi perhitungan biasa.
Pada pertemuan pertama, Bapak Dr. Ir. Achmad Engkos mengatakan bahwa mata kuliah metnum merupakan lanjutan dari mata kuliah matematika teknik. Adanya metode numerik memungkinkan kita untuk dapat menghitung suatu fungsi yang rumit yang biasanya hanya dapat dilakukan dengan kalkulator.
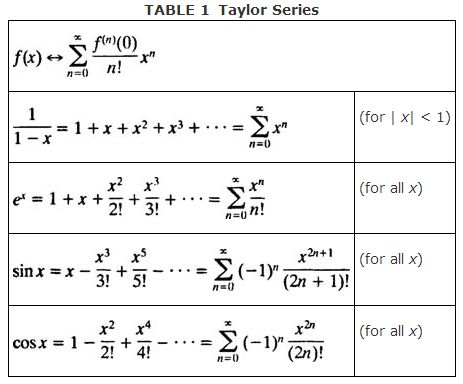
Khusus untuk pengajaran hari ini, formula yang akan digunakan adalah deret Taylor. Deret Taylor adalah suatu deret yang menggunakan suku berulang hingga tak berhingga dengan fungsi f(x) yang diberikan, untuk mencari nilai pendekatan dari fungsi f(x) sebelumnya, berdasarkan dari nilai x yang ditentukan.
Pertemuan 2 (10 September 2019)
Pseudocode adalah sebuah kode yang digunakan untuk menulis sebuah algoritma dengan cara yang bebas yang tidak terikat dengan bahasa pemrograman tertentu. Pseudo berarti imitasi dan code berarti kode yang dihubungkan dengan instruksi yang ditulis dalam bahasa komputer (kode bahasa pemrograman). Apabila diterjemahkan secara bebas, maka pseudocode berarti tiruan atau imitasi dari kode bahasa pemrograman.
Pseudo code sinus
i=1, err=1; suku=x sin=suku while err>1e-7
ratio=-(x^2)/(2*i)/(2*i+1)
suku=suku*ratio
err=abs(suku/sin)
sin=sin+suku
i=i+1
Pseudo code kosinus
i=1, err=1; suku=1 cos=suku while err>1e-7
ratio=-(x^2)/(2*i)/(2*i-1)
suku=suku*ratio
err=abs(suku/cos)
cos=cos+suku
i=i+1
Pseudo code eksponensial
i=1, err=1; suku=1 exp=suku while err>1e-7
ratio=(x^2)/i
suku=suku*ratio
err=abs(suku/exp)
exp=exp+suku
i=i+1
Setelah itu membahas bahasa pemograman. Bahasa Pemrograman merupakan sebuah instruksi untuk memerintah komputer agar bisa menjalankan fungsi tertentu, namun hanya instruksi standar saja.Fungsi dari bahasa pemrograman adalah untuk memerintahkan sebuah komputer agar bisa mengolah data sesuai dengan yang kita inginkan. Jadi, kendali sepenuhnya ada di tangan kita.
Jenis-jenis Bahasa Pemrograman, dimana bahasa pemrograman yang umum diketahui ialah,
Bahasa C Java Phyton
Pertemuan 3 (17 September 2019)
Pada pertemuan ketiga kali ini kita belajar tentang materi turunan numerik. Turunan Numerik bertujuan untuk memudahkan kita untuk menurunkan suatu persamaan yang kompleks. Biasanya, untuk menghitung turunan diperlukan adanya alat bantu seperti kalkulator atau komputer. Turunan numerik menentukan hampiran nilai fungsi turunan f yang diberikan dalam bentuk tabel. Ada 3 pendekatan dalam turunan numerik yaitu hampiran selisih maju, hampiuran selisih mundur, fan hampiran selisih pusat.
Pertemuan 4 (24 September 2019)
Pada pertemuan keempat, Pak Engkos mengajarkan kelas Metode Numerik dengan materi Secant Method, Bisect Method, dan Newton Raphson Method.
Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik. Tujuan metode secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f‘ (x). Fungsi metode secant adalah untuk menaksirkan akar dengan menggunakan diferensi daripada turunan untuk memperkirakan kemiringan/slope. Algoritma Metode Secant 1. Definisikan fungsi F(x) 2. Definisikan torelansi error (e) dan iterasi maksimum (n) 3. Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu x0 dan x1,sebaiknya gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan. 4. Hitung F(x0) dan F(x1) sebagai y0 dan y1 5. Untuk iterasi I = 1 s/d n atau |F(xn)| Xn+1 = Xn – Yn (Xn – Xn-1 / Yn – Yn-1)
metode Newton (juga dikenal sebagai metode Newton-Raphson), yang mendapat nama dari Isaac Newton dan Joseph Raphson, merupakan metode yang paling dikenal untuk mencari hampiran terhadap akar fungsi riil. Metode Newton sering konvergen dengan cepat, terutama bila iterasi dimulai “cukup dekat” dengan akar yang diinginkan. Namun bila iterasi dimulai jauh dari akar yang dicari, metode ini dapat meleset tanpa peringatan. Implementasi metode ini biasanya mendeteksi dan mengatasi kegagalan konvergensi.
Metode Bisect (Bagi-Dua) adalah algoritma pencarian akar pada sebuah interval. Interval tersebut membagi dua bagian, lalu memilih dari dua bagian ini dipilih bagian mana yang mengandung akar dan bagian yang tidak mengandung akar dibuang. Hal ini dilakukan berulang-ulang hingga diperoleh akar persamaan atau mendekati akar persamaan. Metode ini berlaku ketika ingin memecahkan persamaan f(x)=0 dengan f(x) merupakan fungsi kontinyu.
Pertemuan 5 (1 Oktober 2019)
Pada pertemuan ini, kami diajarkan tentang Truncation Errors and Validations. Jika ingin memvalidasi hasil perhitungan numerik terkadang hasilnya kurang logis. Hal ini dikarenakan pada eksperimen error berbeda dengan error pada numerik. Pad numerik, errornya antara lain, rounding error, truncation error, kesalahan asumsi, dan penyederhanaan, sementara pada eksperimen hanya ada error alat ukur. Jadi apa gunanya numerik? Pada sebuah kotak, pada eksperimen mungkin hanya bisa mengukur temperature pada boundary saja, tetapi numerik bisa menghitung hingga bagian dalamnya. Hasil dari metode numerik tidak akan bisa sama dengan eksperimen, tetapi hanya mungkin memiliki trend yang sama. Misalnya, pada eksperimen grafik yang didapat cendrung turun, begitu juga pada numerik, artinya numerik masih bisa dapat kita percayan sebagai alat untuk Analisa. Jika hal ini terpenuhi, maka hasil eksperimen dapat kita Analisa dengan menggunakan metode numerik terutama pada bagian-bagian yang tidak dapat diukur oleh eksperimen.
Pertemuan 6 dan Tugas 1 (29 Oktober 2019)
Materi yang difokuskan oleh Pak Dai adalah Python. Pada setiap PC kelas Metnum sudah terdapat aplikasi Python yang dapat digunakan setiap Mahasiswa. Python sendiri adalah salah satu metode agar manusia dapat berkomunikasi dengan komputer serta tentunya mempermudah pekerjaan manusia. Terdapat beberapa perintah mudah yang diterapkan pada kelas hari ini. Seperti penjumlahan angka dan kata-kata. Contohnya sebagai berikut:
>>>a = 50
>>>b = 25
>>>a+b
75
Selanjutnya Pak Dai juga turut menjelaskan secara singkat bagian-bagian Python diantaranya IDE dan Shell dimana IDE adalah interpretasi dan tempat membuat coding komputer, sedangkan Shell merupakan tempat kita menjalankan program yang telah dibuat. Setelah pengenalan tentang python pak Dai menjelaskan kembali alur berpikir dari metode numerik yang merupakan bgaimana membuat penyelesaian terhadap sebuah masalah matematis.
kemudian beliau mengenalkan salah satu cara berpikir runge-kutta.
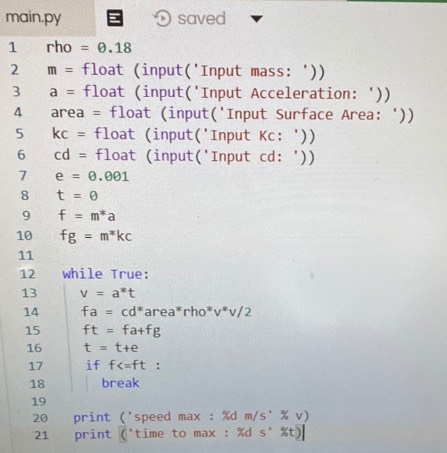
Untuk tugas yang diberikan kepada Mahasiswa adalah membuat aplikasi yang dapat mengukur top speed dari sebuah kendaraan. Kelompok saya berdiskusi dan mendapatkan gambaran umum dari persamaan yang akan digunakan yaitu sebagai berikut:
Penyelesaian soal menggunakan model Governing equation pada mobil yang memiliki percepatan, gesekan, dan hambatan udara adalah:

Pertemuan 7 (5 November 2019)
Pada pertemuan kali ini mahasiswa diajarkan metode runge-kutta.
Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi, dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f(x, y) pada titik terpilih dalam setiap selang langkah [CON80]. Metode Runge-Kutta adalah metode PDB yang paling popuper karena banyak dipakai dalam praktek. Bentuk umum metoda Range-Kutta orde-n ialah: yr+1 = yr + a1k1 + a2k2 + ... + an kn
dengan a1, a2, ..., an adalah tetapan, dan
k1 = hf (xr , yr)
k2 = hf (xr + p1h, yr + q11k1)
k3 = hf (xr + p2h, yr + q21k1 + q22k2)
kn = hf (xr + pn-1h, yr + qn-1,1 k1 + qn-1,2 k2 + ... + qn-1, n-1 kn-1)
Nilai ai, pi, qij dipilih sedemikian rupa sehingga meminimumkan galat per langkah, dan persamaan (P.8.24) akan sama dengan metode deret Taylor dari orde setinggi mungkin.
Galat per langkah metode Runge-Kutta orde-n : O(hn+1)
Galat longgokan metode Runge-Kutta orde-n : O(hn)
Orde metode = n
Lalu, mahasiswa mempelajari perangkat lunak CFDSOF-NG. Untuk mempelajari aliran fluida. Langkah yang diajarkan menggunakan CFDSOF
CFDSOF adalah sebuah program komputer modular berbasis Computational Fluid Dynamics (CFD) untuk pemodelan aliran fluida dan fenomena yang terkait dengannya seperti pindah panas dan reaksi kimia. Dengan CFDSOF Anda dapat secara cepat melakukan analisis masalah-masalah aliran fluida yang rumit walaupun tidak memiliki keahlian khusus di bidang pemrograman komputer. CFDSOF memungkinkan Anda menerapkan metoda-metoda simulasi untuk menganalisis dan menyelesaikan masalah-masalah desain praktis. Software ini menggunakan teknik-teknik pemodelan numerik muatkhir dan rentang model fisika yang luas dan sudah teruji untuk mensimulasikan berbagai jenis atau tipe aliran fluida. Simulasi ini dilakukan secaramudah dengan bantuan graphical user interface (gui) dan command user interface (cui) untuk input permasalahan, komputasi dan pemrosesan hasil perhitungan dengan grafis (visualisasi). Awalnya kami diajarkan untuk menyetel terlebih dahulu ketentuan-ketentuan di CFD-Pre dan CFD-Solve. Selain seluruh ketentuan sudah di terapkan, kami pun perlu untuk memvariasikan kecepatan inlet di mobil. Kelompok saya memvariasikan kecepatan inlet mulai dari 10m/s hingga 100m/s dengan perbedaan tiap kecepatannya adalah 10m/s. Sehingga didapat 10 data yang berbeda di drag force terakhir.
Pertemuan 8 (12 November 2019)
Pada pertemuan kali ini kami diberikan materi tentang cara menggunakan CFDSOF khususnya cara menganalisis suatu fluida yang berjalan pada suatu mobil. Hasil dari simulasi ini kemudian dijadikan tugas kelompok dimana mencari rumus persamaan gaya hambat dari kecepatan.
Pertemuan 9 (19 November 2019)
Pada pertemuan kali ini membahas mengenai materi Optimasi. Selain itu juga materi Airfoil sebagai masalah nyata berikutnya. Tugas yang diberikan pada pertemuan ini adalah untuk mecari ratio koef Lift/coef Drag dengan pemilihan Angle Of Attack sebagai variasi data yang dipilih. Namun untuk sekarang, kita hanya perlu mecari grafik koef Lift dan koef Drag. Untuk model Airfoil, keputusan ini diberikan ke setiap anggota grup.
Untuk instruksi dari tugas nya adalah :
Cari/Buat airfoil.
Buat Angle Of Attack dan buat menjadi variasi data.
Simpan setiap data sebagai format .stl.
Simulasikan di aplikasi CFD-SOF
Cari Force Drag dan Force Lift
Optimasi Fdrag/FLift terendah/minimal
Pertemuan 10 (26 November 2019)
Pada pertemuan kali ini Pak Dai memberikan kuis metode numerik
Pertemuan 11 (3 Desember 2019)
Pada pertemuan ini, beberapa kelompok mempresentasikan mengenai optimasi airfoil yang mereka lakukan.
Airfoil adalah bentuk dari suatu sayap pesawat yang dapat menghasilkan gaya angkat (lift) atau efek aerodinamika ketika melewati suatu aliran udara.
Cara Kerja Sayap Udara yang mengalir diatas sayap lebih cepat dari udara yang mengalir dibawah sayap, sehingga tekanan udara diatas pesawat lebih rendah.
Metode Optimasi Goplden Section
Golden section method merupakan modifikasi dari bisection method untuk mencari nilai optimum dari suatu kurva dalam range tertentu. Cara kerja Golden Section Method adalah dengan membatasi range kita dengan nilai minimum dan maksimum, a dan b.
Pertemuan 12 (10 Desember 2019)
Pada pertemuan kali ini kami membahas tentang Artifical Neural Networks.
Neural Network merupakan kategori ilmu Soft Computing. Neural Network sebenarnya mengadopsi dari kemampuan otak manusia yang mampu memberikan stimulasi/rangsangan, melakukan proses, dan memberikan output. Output diperoleh dari variasi stimulasi dan proses yang terjadi di dalam otak manusia. Kemampuan manusia dalam memproses informasi merupakan hasil kompleksitas proses di dalam otak. Misalnya, yang terjadi pada anak-anak, mereka mampu belajar untuk melakukan pengenalan meskipun mereka tidak mengetahui algoritma apa yang digunakan. Kekuatan komputasi yang luar biasa dari otak manusia ini merupakan sebuah keunggulan di dalam kajian ilmu pengetahuan.
Fungsi dari Neural Network diantaranya adalah:
Pengklasifikasian pola
Memetakan pola yang didapat dari input ke dalam pola baru pada output
Penyimpan pola yang akan dipanggil kembali
Memetakan pola-pola yang sejenis
Pengoptimasi permasalahan
Prediksi