Metode Numerik Asistensi 2021
Contents
About
- Edo Syafei PMDSU
- Candra Damis Widyawati S3
- Josiah Enrico M 19
- Christopher S. Erwin M 18
- Rijal Ghodi M 18
Introduction to Programming
under construction
OpenModelica
OpenModelica adalah aplikasi yang digunakan untuk melakukan pemodelan. OpenModelica memudahkan penyelesaian permasalahan permodelan sistem yang cukup rumit. Coding yang dilakukan dalam OMEdit ditulis berdasarkan bahasa C++.
OpenModelica digunakan untuk kelas Metode Numerik untuk beberapa alasan:
- OpenModelica memampukan kita untuk melakukan pemodelan sitem teknik dengan mudah tanpa terlalu mendalami pengetahuan pemograman dan ilmu komputer.
- OpenModelica adalah software yang Open Source, dengan akses bebas dan terbuka. Karena itu, terdapat banyak pengguna dan software dapat digunakan gratis dengan bebas secara legal.
Class & Function
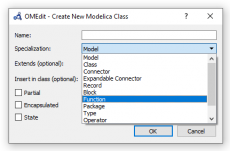
Ketika membuat file Class baru di OpenModelica, ada pilihan Specialization dimana jenis Class dapat dipilih. Setiap Class mempunyai karakteristik dan tujuan masing-masing. Informasi lebih lanjut tentang setiap jenis Class bisa dibaca dalam dokumentasi disini.
Salah satu jenis Class yang sudah digunakan adalah Model yang dapat melakukan pemodelan dan simulasi. Ada jenis Class lain yaitu Function dimana code yang diketik di dalamnya akan menjadi suatu fungsi yang dapat dipanggil dalam model. Ketika dibuat, Function mempunyai bagian algorithm dimana perhitungan fungsi dimasukkan. Sebelum bagian algorithm, dapat dimasukkan input dan output yang akan ditangani oleh fungsinya.
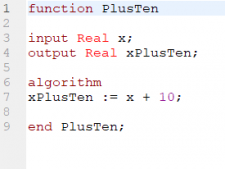
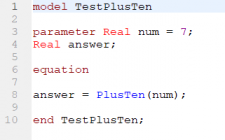
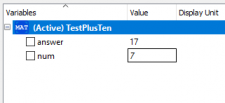
Sebagai contoh, dibikin suatu fungsi PlusTen yang menambahkan angka 10 ke nilai input x. Fungsi ini terus akan dipanggil dalam model TestPlusTen yang menerima parameter num dan menghasilkan variabel answer. Ketika dicompile, hasil penggunaan fungsi di model ini dapat dilihat.
Contoh fungsi yang menambahkan 10 ke nilai input.
Fungsi dipanggil dalam model.
Hasil model yang menggunakan fungsi.
under construction
Python
Phyton adalah bahasa pemrograman tingkat tinggi yang dewasa ini menjadi standar dalam dunia komputasi ilmiah. Meski begitu, python memiliki struktur kode yang ringkas, fleksibel, dan mudah terbaca. Tersedia secara open source dan multiplatform, Python bisa menjadi opsi terbaik untuk dipelajari oleh bagi mahasiswa yang baru mengenal dunia komputasi.
Selain itu, banyak developer-developer dari belahan dunia berlomba-lomba membuat modul yang “gratis” untuk menunjang kemudahan bahasa Python. Dua modul yang sangat bermanfaat untuk dunia komputasi adalah: NumPy dan SciPy. Ke depan dua modul ini akan dibahas lebih lanjut.
Instalasi
Ada 2 aplikasi minimal yang harus diinstal, yakni Phyton dan IDE Phyton. Python adalah aplikasi dasar dan otak dari komputasi sedangan IDE (Integrated Development Environment) adalah jembatan user untuk menulis, mengedit, mengcompile, dan men-debug kode komputasi Python. Ada beberapa jenis IDE: Spyder, Pycham, Jupiter, Visual Studio Code, dan lain-lain. Namun kali ini, akan digunakan IDE Spyder.
Aplikasi Python dapat diunduh di sini IDE Spyder dapat diunduh di sini Terdapat banyak sekali dokumentasi Python yang dapat digunakan untuk bahan pembelajaran. Link-link berikut dapat menjadi referensi: link 1, link 2, link 3. Tutorial python dalam bahasa indonesia dapat dilihat pada link beikut.
Sintaks Dasar
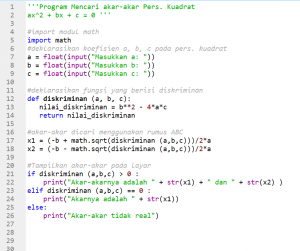
Berikut adalah contoh program pencarian akar-akar persamaan kuadrat menggunakan rumus ABC:
Sourcecode untuk program pencarian akar persamaan kuadrat.
Hasil Running.
Ketika program di-run, di layar monitor akan muncul perintah kepada user untuk memasukkan koefisien a, b, dan c persamaan kuadrat. Kemudian python akan mengolahnya dan mengirim output berupa akar persamaan kudarat tsb. Penjelasan lebih detail tentang sintaks program di atas adalah sebagai berikut:
Komentar
Pada baris pertama sampai baris kedua, terdapat multiline comment, ditandai dengan adanya tiga tanda petik di awal dan di akhir komentar. Komentar ini tidak akan di-compile, berfungsi untuk memberikan informasi program dan memudahkan user untuk membaca kode. Selain multine comment, terdapat juga single line comment, contohnya pada baris ke 4, 6, 11, 16 dan 20, ditandai dengan adanya tanda pagar (#) pada awal komentar. Lebih lanjut tentang komentar dijelaskan di link berikut.
Import Modul
Pada baris kelima, terdapat statement import math, ini adalah statement untuk memanggil modul math, modul yang berisi operasi-operasi matematika dasar, seperti sqrt, log, ln, dst. Selain modul math, ada beberapa modul yang harus diketahui dalam kaitannya dengan komputasi, yakni modul matplotlib (untuk membuat plotting), modul numpy (untuk membuat matriks dan vektor), dan modul scipy (untuk perhitungan scientific). Modul-modul ini tidak built-in di dalam library python, tetapi harus diinstal. Cara instalnya adalah dengan pergi ke command prompt, kemudian tulis kode berikut (untuk python versi 3.9.4): python -m pip install nama_modul Informasi lebih lanjut mengenai modul dapat dilihat di sini
Deklarasi Variabel
Pada baris ke 7 sampai 9, terdapat deklarasi variabel a, b, dan c yang merupakan koefisien masing-masing suku persamaan kuadrat. Nama variabel bersifat case sensitive dan tidak boleh memakai nama-nama modul python. Pendeklarasian variabel harus dijembatani dengan tanda 'sama dengan' (=). Kemudian isi variabel bisa apa saja. Dalam program di atas, variabel a, b, dan c, berisi angka real yang diambil dari inputan user.
Kode a = float(input("Masukkan a: ")) dapat dibaca sebagai berikut: Pada layar, akan muncul tulisan Masukkan a: , kemudian ketika user mengetikkan angka ke layar maka angka tersebut akan menjadi variabel a. Akan tetapi karena semua inputan karakter dari user dianggap sebagai data string oleh python, maka ditambahkanlah sintaks float() agar tipe data user menjadi float.
Tipe data di dalam python kurang lebih ada 5, tersaji pada tabel berikut:
Tipe-tipe data pada Python.
Penjelasan lebih lanjut mengenai tipe data python dapat dilihat di sini
Operator
Masing-masing objek di dalam python dapat dioperasikan. Berikut beberapa jenis operasi pada python:
1. Operator Aritmatika, yakni: + (penjumlahan), - (pengurangan), * (perkalian), / (pembagian), dan % (sisa pembagian). Contoh penggunaan operasi aritmatika ada di baris ke 13, 17, dan 18.
2. Operator Penugasan, yaitu operator yang berfungsi untuk memberikan tugas kepada variabel, contoh: = (pengisian variabel), += (penjumlahan variabel dengan suatu bilangan), dll.
3. Operator Pembanding, gunanya untuk membandingkan dua objek, outputnya berupa True atau False. Berikut operator pembanding: == (Sama dengan), > (Lebih dari), < (Kurang dari), >= (Lebih dari sama dengan), != (Tidak sama dengan), dll.
4. Operator Logika, yaitu operator yang berfungsi untuk menilai pernyataan-pernyataan kondisional. Outputnya adalah True atau False. Contoh: and (True jika dua pernyataan benar), or (True jika salah satu dari dua pernyataan benar), not (True jika pernyataan salah).
Fungsi
Fungsi adalah program kecil di dalam main program. Dengan fungsi kita dapat melakukan perhitungan yang sama berkali-kali tanpa menulis sintaks yang sama berkali-kali. Misalnya pada contoh di atas, fungsi diskriminan (a, b, c) pada baris ke -12 digunakan untuk mencari diskriminan persamaan kuadrat. Diskriminan ini kemudian digunakan di tiga tempat berbeda, pertama ketika mencari x1 (akar pertama), lalu x2, dan terakhir untuk menentukan jenis akar (real beda, real kembar, tidak real). Daripada menulis ulang rumus diskriminan, b^2 - 4ac, lebih baik dibuatkan fungsi diskriminan.
Fungsi harus ditulis dengan sintaks berikut:
def nama_fungsi (variabel1, variabel2):
statement1
statement2
return nama_variabel_yang_ingin_dikembalikan_nilainya
variabel1 dan variabel2 nantinya akan dioperasikan di dalam statement1 dan statement2. Kemudian nama_variabel_yang_ingin_dikembalikan_nilainya akan direturn atau dikembalikan sebagai output dari fungsi tsb.
If Else
Systems of Linear Algebraic Equations
under construction
Gauss Elimination Method
under construction
LU Decomposition Methods
under construction
Curve Fitting
under construction
Numerical Methods
under construction
Bracketing Methods
under construction
Bisection Method
under construction
False Position (Regula Falsi)
under construction
Open Methods
under construction
Newton-Raphson Method
under construction
Secant Method
under construction
Optimization
under construction
Newton's Method
under construction
Parabolic Method
under construction
Golden Section Search
under construction
Powell's Method
Powell's method (Powell's conjugate direction method) is an algorithm proposed by Michael J. D. Powell for finding a local minimum of a function. The function need not be differentiable, and no derivatives are taken. The algorithm iterates an arbitrary number of times until no significant improvement is made. Powell's method can be used for multivariable optimization.
under construction
Case Studies
under construction
2D Truss Analysis
under construction
3D Truss Optimization
under construction
