Metnum03-Muhammad Rifqi Dwitama
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
Assalamualaikum wr. wb.
Biodata Diri
Nama : Muhammad Rifqi Dwitama
NPM : 1706024476
Agama : Islam
Program Studi : S1 Teknik Mesin Paralel
Contents
Sebelum UTS
Sebelum UTS kami mempelajari cara mencari akar menggunakan dua metode, yaitu bracketing methods dan open methods.
Pada bracketing methods terdapat:
- Graphical Methods
- metode mencari akar dengan membuat grafik fungsi dan melihat letak perpotongan dengan sumbu x
- Bisection Methods
- False-Position Methods
Pada open methods terdapat:
- Simple Fixed-Point Iteration
- Newton-Raphson Methods
- Secant Methods
- Brent's Method
Setelah itu kita juga mempelajari regresi dan interpolasi linear.
Pertemuan Pertama 9 November 2020
Pada pertemuan pertama saya dengan Pak Indra pada kelas Metode Numerik, saya diminta untuk menginstall dan juga mempelajari software OpenModelica yang bertujuan untuk mensimulasikan suatu sistem yang didistribusikan dalam bentuk kode sumber dan biner untuk penelitian. sebelumnya saya juga diminta untuk mempelajari makna dari belajar tentang metode numerik, dengan diadakannya diskusi 2 arah antara dosen yaitu Pak Dai dengan mahasiswanya. Pembahasan ini meliputi tentang fenomena apa saja yang dapat kita dapat dari metode numerik dan dikaitkan dengan kehidupan sehari-hari seperti konsep "tak hingga" dan juga "infinita" dilihat dari sudut pandang seorang engineer.
Pertemuan Kedua 16 November 2020
Pada kali ini Bapak Indra memberi tugas untuk membuat suatu program sederhana yang dimana program tersebut di koding pada openmodelica,Berikut ialah penjelasan menggunakan openmodelica untuk mencari mean pada suatu data:
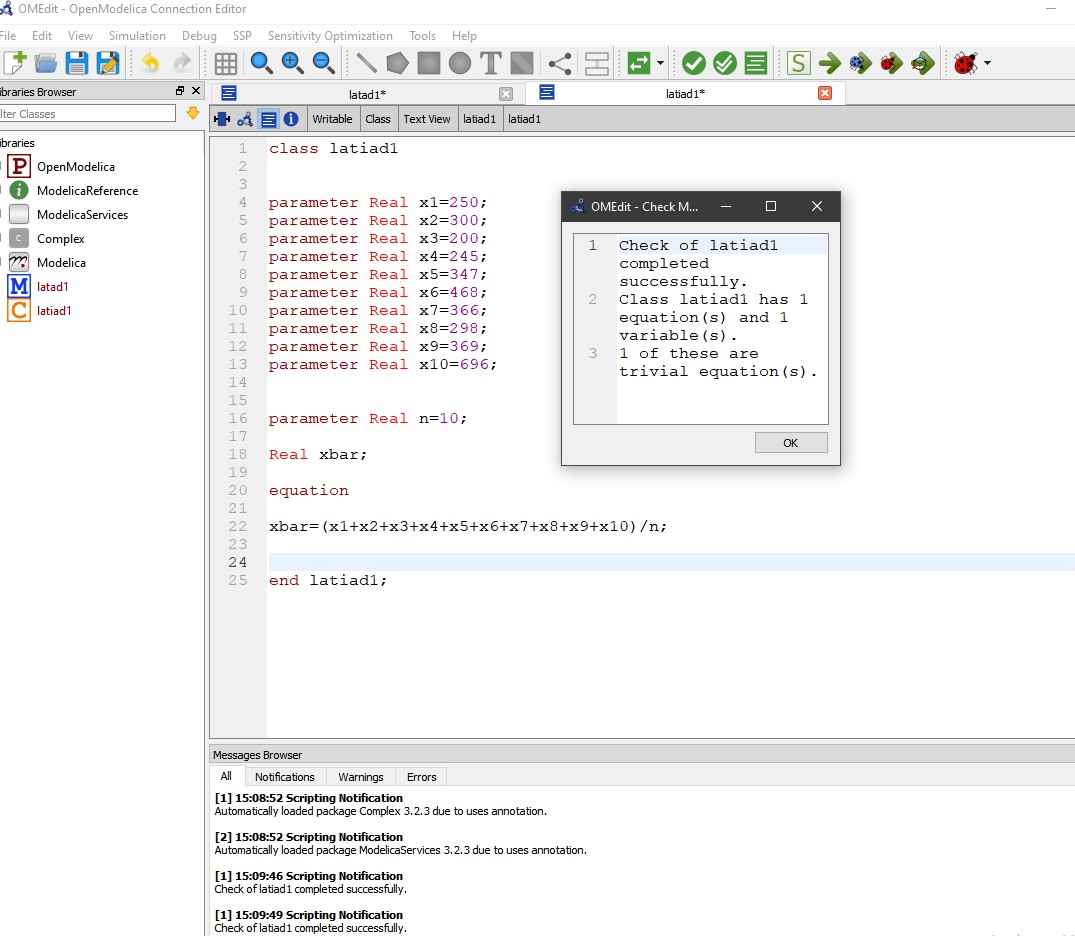
1.Menginput data,nilai yang dicari dan equation yang digunakan class latih1add
parameter Real x1=250; parameter Real x2=300; parameter Real x3=200; parameter Real x4=245; parameter Real x5=347; parameter Real x6=468; parameter Real x7=366; parameter Real x8=298; parameter Real x9=369; parameter Real x10=696;
parameter Real n=10;
Real xbar;
equation
xbar=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10)/n;
end latih1add;
Disini kita menginput data data yang dibutuhkan pada persoalan ini saya mengambil sampel 10 data.Hal tersebut kita masukan ke parameter real seperti gambar diatas.Parameter real digunakan untuk memberi informasi data yang diketahui.Setelah itu menulis "real" untuk angka yang dicari.Setelah data yang diketahui dan ditanyakan sudah dilakukan maka kita langsung menulis equation yang dimana equation pada data ini ialah
xbar=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10)/n;
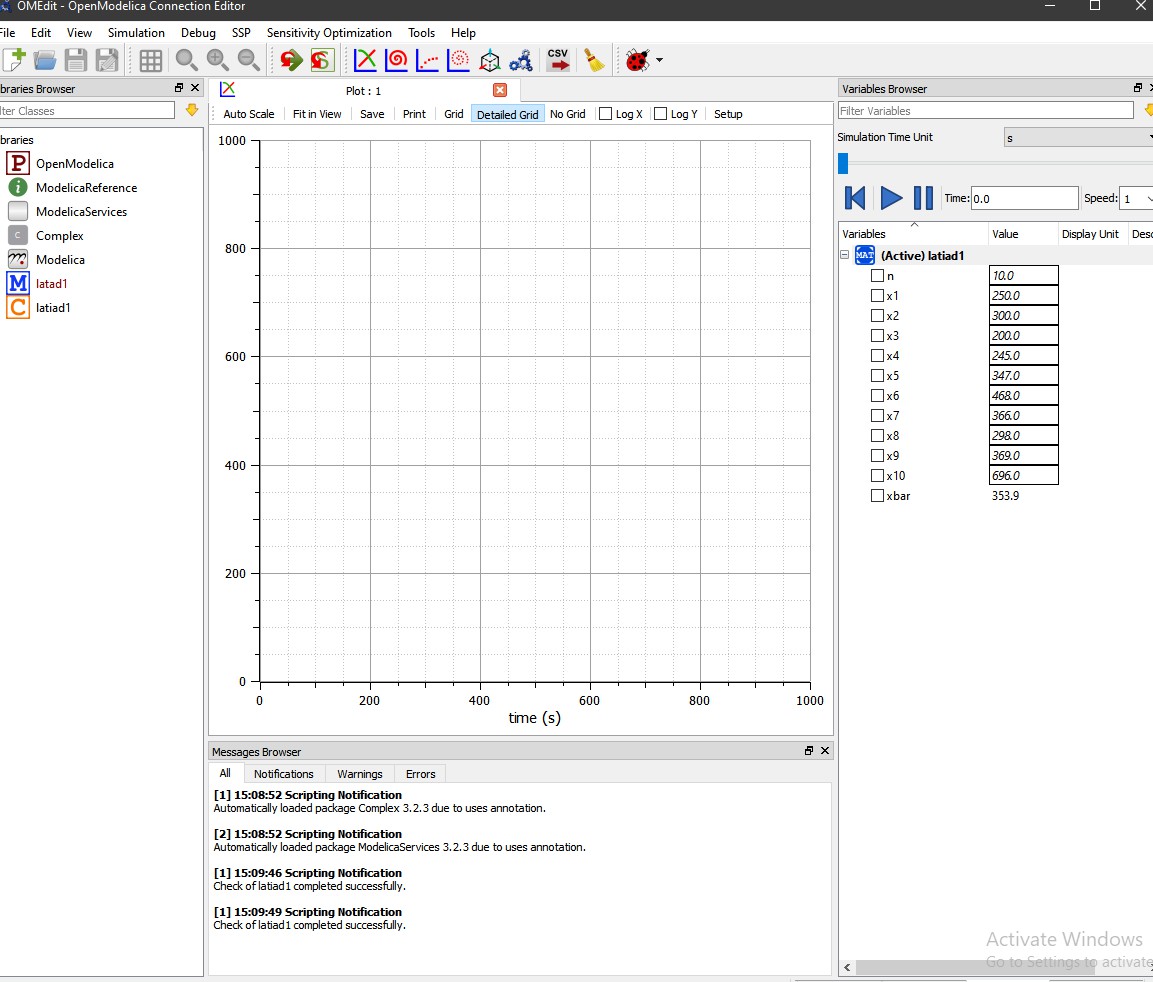
2.Mengecek dari program yang kita buat
Tugas 2
Persamaan aljabar simultan tersebut dapat diselesaikan dengan matematik secara umum seperti Gauss Elimination, atau menggunakan metode lain seperti Gauss Elimination yang melibatkan matriks,atau Gauss Seidel.Pada persoalan dibawah ini saya akan menggunakan metode Gauss Elimination untuk menyelesaikan persamaan berikut.
class test Real A[5,5] = [10,-1,2,12,7;-1,11,-1,9,8;2,-1,10,-1,8;0,3,-1,8,8;12,23,44,56,87];
Real B[5] = {6,25,-11,15,89};
Real X[5];
function solve
extends Modelica.Icons.Function; input Real A[:, size(A, 1)] "Matrix A of A*x = b"; input Real b[size(A, 1)] "Vector b of A*x = b"; output Real x[size(B, 1)] "Vector x such that A*x = b";
end solve;
algorithm
X := Modelica.Math.Matrices.solve(A,B);
end test;
Eliminasi Gauss adalah algoritme yang digunakan untuk menyelesaikan sistem persamaan linear. Metode ini dinamai dari matematikawan Carl Friedrich Gauss,
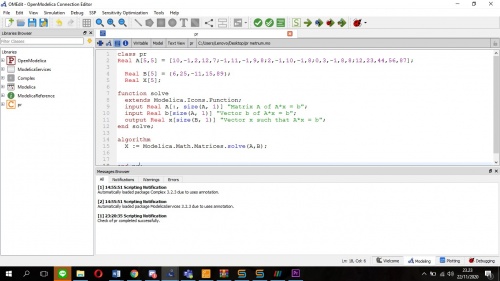
Pada aplikasi OpenModelica terdapat model untuk menyelesaikan permasalahan aljabar simultan dengan menggunakan metode Gauss Elimination.Berikut ialah model yang saya buat dengan software OpenModelica:
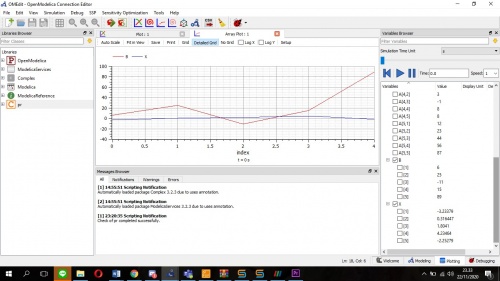
Saya menggunakan perintah yang ada di library modelica yaitu "Modelica.Math.Matrices.solve(A,b)" untuk menyelesaikan sistem persamaan linier eliminasi gauss yang ada diatas.Setelah melakukan pengecekan dan melakukan simulasi terhadap model yang telah saya buat,selanjutnya melakukan plotting terhadap hasil simulasi tersebut. Berikut adalah hasil plotting dari simulasi persamaan diatas:
hasil X yang dihasilkan dari penyelesaian persamaan diatas ialah -3.23379 , 0.316447 , 1.8041 , 4.23464 , -2.25279
Pertemuan Ketiga 23 November 2020 ==
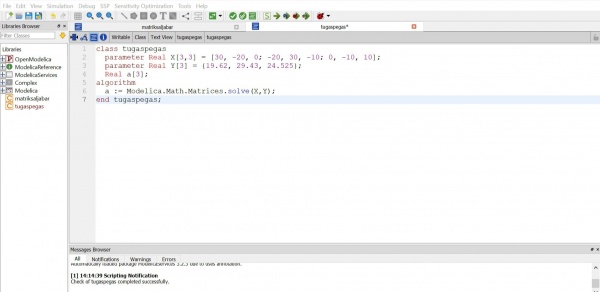
Pada pertemuan ketiga kami diminta untuk menjelaskan tugas minggu lalu yaitu Penyelesaian Persamaan Aljabar Simultan. Setelah itu kami juga diminta untuk membuktikan sebuah persoalan mengenai pegas menggunakan OpenModelica. Disini saya menggunakan function yang sudah saya buat untuk tugas minggu lalu dan membuat class baru sebagai berikut:
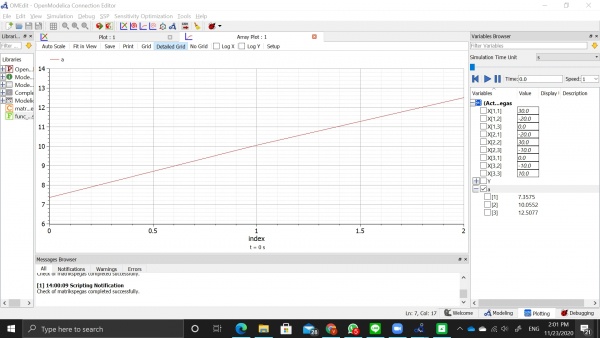
Setelah itu dapat kita lakukan simulasi untuk mendapatkan hasil dan grafik seperti pada gambar dibawah ini. Didapatkan hasil yaitu:
a1 = 7.3575
a2 = 10.0552
a3 = 12.5077
Maka dapat kita simpulkan bahwa jawaban yang tertera pada buku sudah sesuai dengan penyelesaian menggunakan OpenModelica.
Tugas 3
menyelesaikan soal yang diberikan pada buku untuk diselesaikan menggunakan modelica
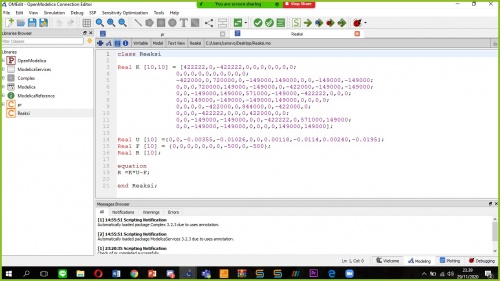
23:28 class Reaksi
Real K [10,10] = [422222,0,-422222,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0;
-422000,0,720000,0,-149000,149000,0,0,-149000,-149000;
0,0,0,720000,149000,-149000,0,-422000,-149000,-149000;
0,0,-149000,149000,571000,-149000,-422222,0,0,0;
0,0,149000,-149000,-149000,149000,0,0,0,0;
0,0,0,0,-422000,0,844000,0,-422000,0;
0,0,0,-422222,0,0,0,422000,0,0;
0,0,-149000,-149000,0,0,-422222,0,571000,149000;
0,0,-149000,-149000,0,0,0,0,149000,149000];
Real U [10] ={0,0,-0.00355,-0.01026,0,0,0.00118,-0.0114,0.00240,-0.0195}; Real F [10] = {0,0,0,0,0,0,0,-500,0,-500}; Real R [10];
equation R =K*U-F;
end Reaksi;
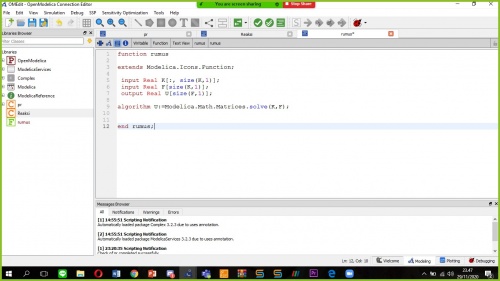
23:29 function rumus
extends Modelica.Icons.Function;
input Real K[:, size(K,1)]; input Real F[size(K,1)]; output Real U[size(F,1)];
algorithm U:=Modelica.Math.Matrices.solve(K,F);
end rumus;
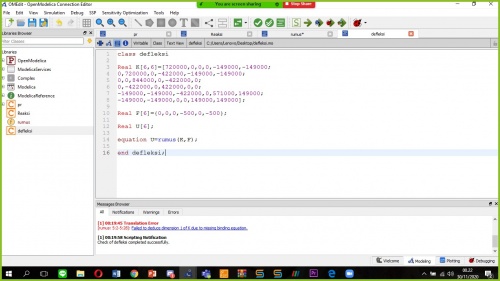
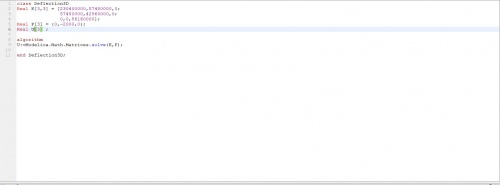
23:29 class defleksi
Real K[6,6]=[720000,0,0,0,-149000,-149000; 0,720000,0,-422000,-149000,-149000; 0,0,844000,0,-422000,0; 0,-422000,0,422000,0,0; -149000,-149000,-422000,0,571000,149000; -149000,-149000,0,0,149000,149000];
Real F[6]={0,0,0,-500,0,-500};
Real U[6];
equation U=rumus(K,F);
end defleksi;
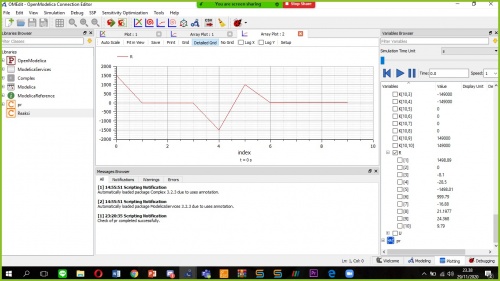
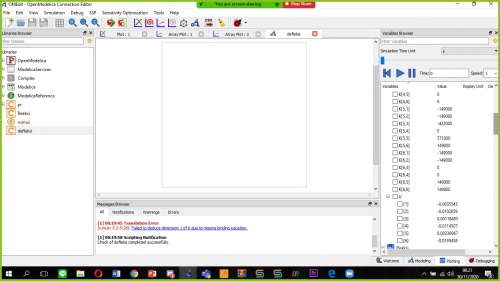
hasil yang diselesaikan dimodelica sama dengan hasil yang sudah diselesaikan dibuku
Pertemuan Keempat 30 November 2020
quiz 1
soal
diselesaikan dengan cara
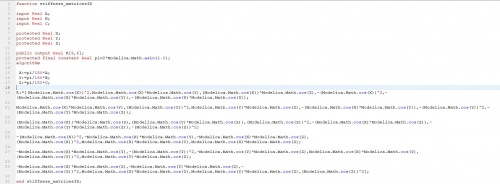
untuk mencari K lokal saya mempunyai fungsi sebagai berikut
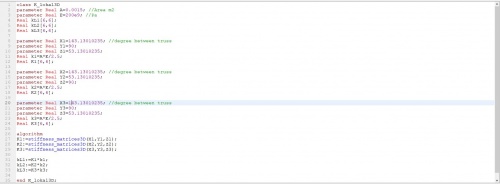
dengan class sebagai berikut
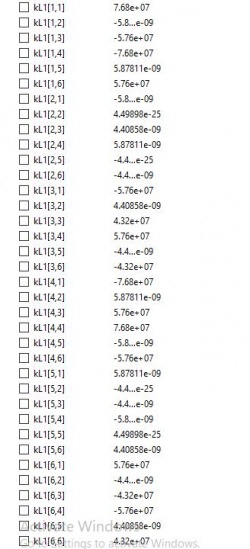
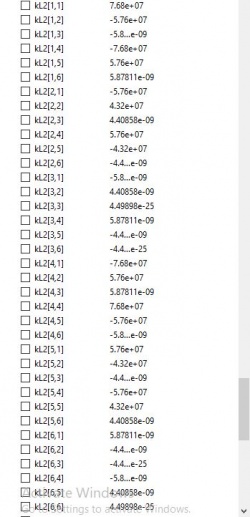
Menghasilkan K lokal sebagai berikut
Setalah itu Kita mencari Defleksi pada soal di atas sebagai berikut
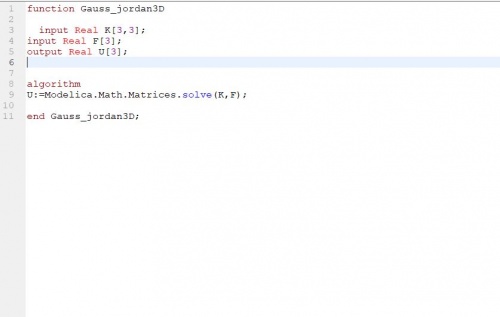
dengan menggynakan fungsi gauss jordan sebagai berikut
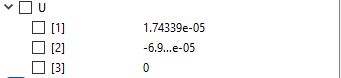
menghasilkan defleksi sebagai berikut
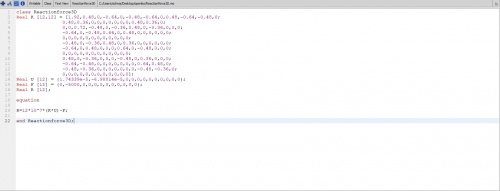
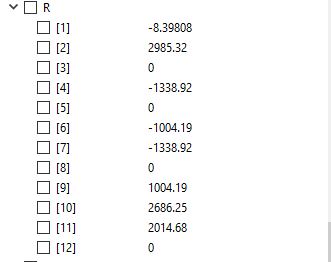
Setelah itu kita mencari reaction yang ada dengan cara sebagai berikut
dengan hasil sebagai berikut :
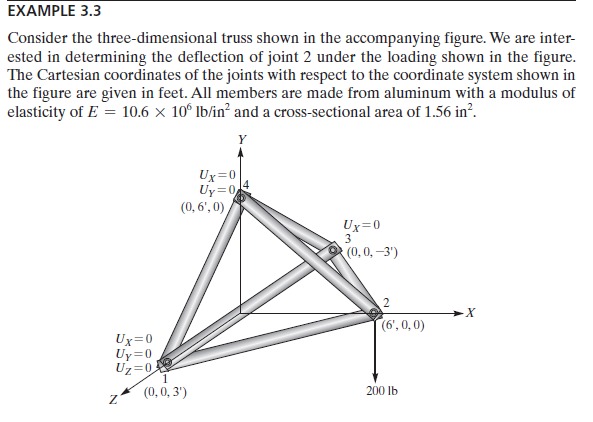
Tugas 05
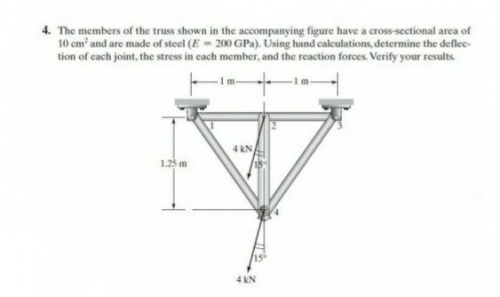
Diketahui pada soal yang tergambar diatas,tahapan pertama kita harus mencari sudut cos x cos y cos z dan L pada gambar tersebut.Disini saya membuat class khusus untuk mendapatkan nilai - nilai yang dicari diatas untuk mengurangi kesalahan perhitungan secara manual dengan class sebagai berikut
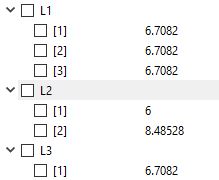
dan mendapatkan hasil sebagai berikut: Berikut ialah untuk L setiap batangnya
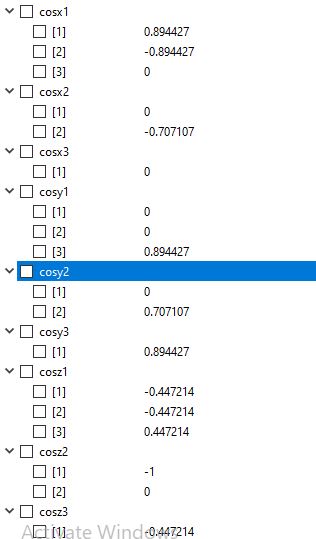
Berikut ialah cos x,y,z yang dibutuhkan :
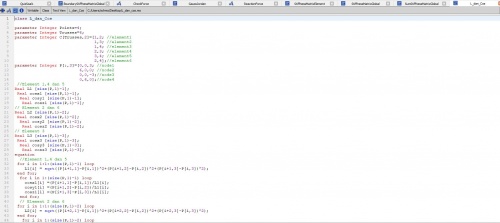
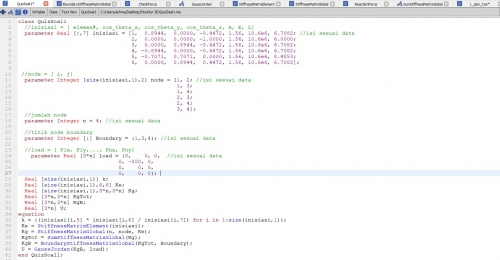
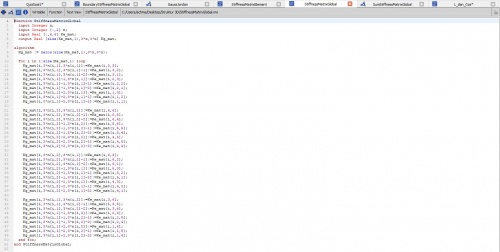
setelah itu saya menggunakan class dan function yang diajarkan oleh ahmad muhammad fahmi yaitu 1 class dengan 6 fungsi pembantunya,berikut ialah class yang dibuat :
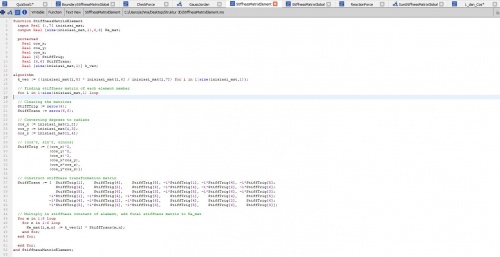
Pada soal ini boundarynya sangat berbeda dikarenakan setiap batangnya ada yang dapat menjadi fix di sumbu xyz,xy,dan x setelah itu tahap kedua ialah kita mencari K lokal di setiap elmentnya dengan fungsi berikut:
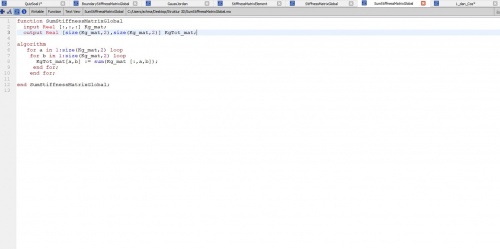
Setelah mendapatkan K lokal sebagai variabel baru kita harus menempatkan K lokal ke K global agar nantinya bisa di satukan menjadi K global total dengan fungsi sebagai berikut:
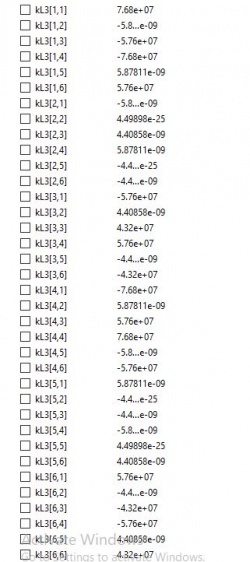
yang dimana pada fungsi ini menghasilkan KG1,KG2,KG3,KG4,KG5 dan KG6 dapat dilihat pada hasil ditandai oleh kg yang dimana (melambangkan elment berapa,baris keberapa,kolom keberapa) Setelah itu kita menjumlahkan KG1 sampai KG6 dengan fungsi sebagai berikut:
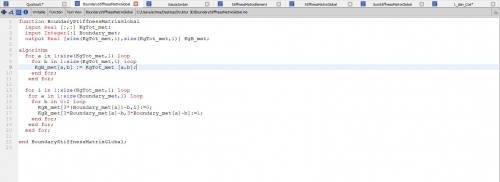
setelah itu kita mendapatkan KG total yang digunakan untuk mencari displacement dan Reaction force dari gambar diatas,tetapi sebelum memasukkan kesana kita harus memberi batasan yang dimana pada soal ini pada node 1 sumbu XYZ = 0,pada node 4 XY = 0 dan pada node 3 X = 0 tetapi saya menggunakan fungsi yang diberikan oleh ahmad muhammad fahmi untuk mengerjakan soal nomor 8 yang dimana dianggap pada node 1,3,4 ialah 0,berikut fungsinya:
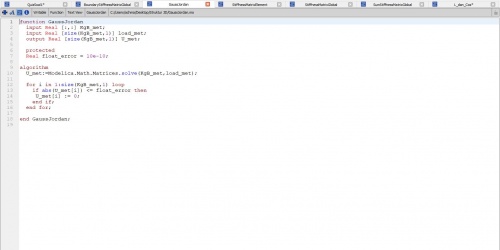
Lalu hasil dari KG total yang diberi boundary dimasukkan ke persamaan gauss jordan yang dimana function dari gauss jordan menggunakan function bawaan dari open modelica sebagai berikut.
berikut ialah hasilnya.
Tugas Besar Metode Numerik
Objektif:
- Mengoptimasi harga pembuatan rangka truss sederhana dengan memvariasi dimensi dan elastisitas material.
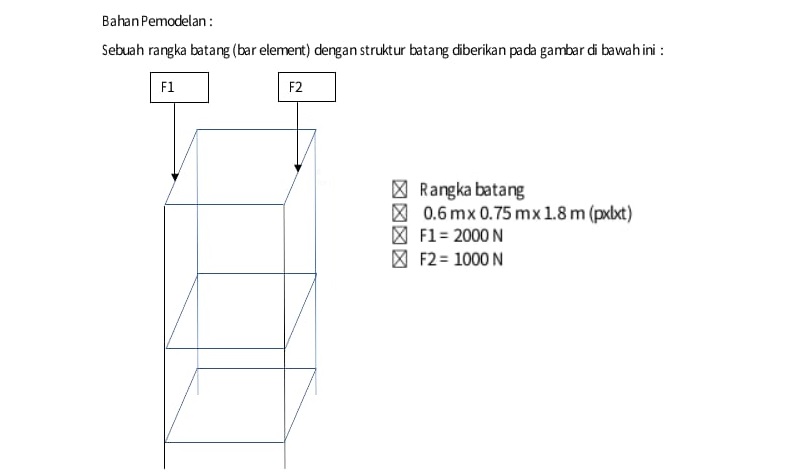
Geometri dan Load
Constraint:
- Spesifikasi L (Panjang) dan geometri rangka truss
- Gaya beban terhadap struktur (1000 N dan 2000 N)
Asumsi:
- Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
- Beban akan terdistribusi hanya pada point penghubung Untuk perhitungan displacement, reaction force, dan stress
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
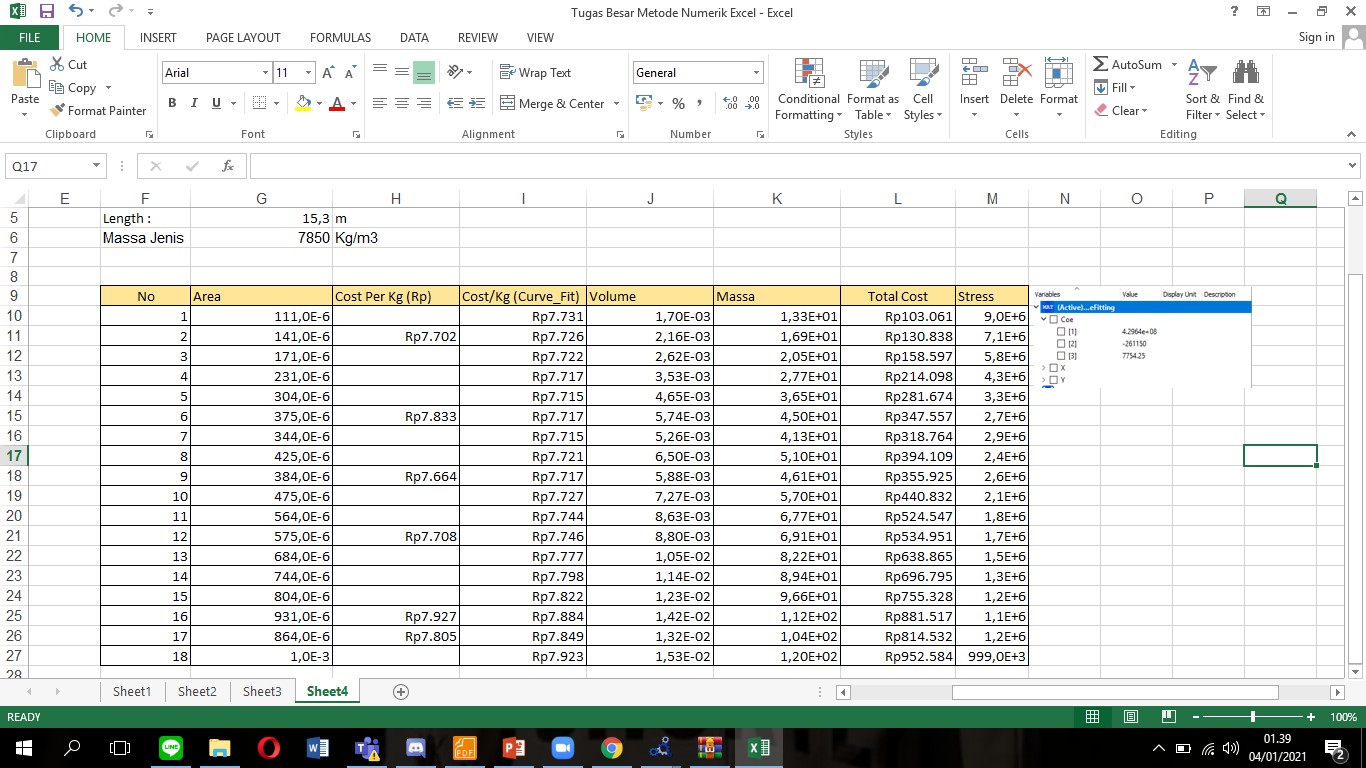
lalu membuat excel yang berisikan tentang data material yang akan digunakann dan harga dari material tersebut:
untuk mendapatkan curve fitting kami diajarkan oleh josiah ahmad dan cristo untuk menggunakan fungsi berikut dengan class yang kami buat sendiri yang dimana sumbu x ialah area dan y adalah harga per kg dari batang tersebut.Disini kami mengasumsikan Elastisitas yang konstan
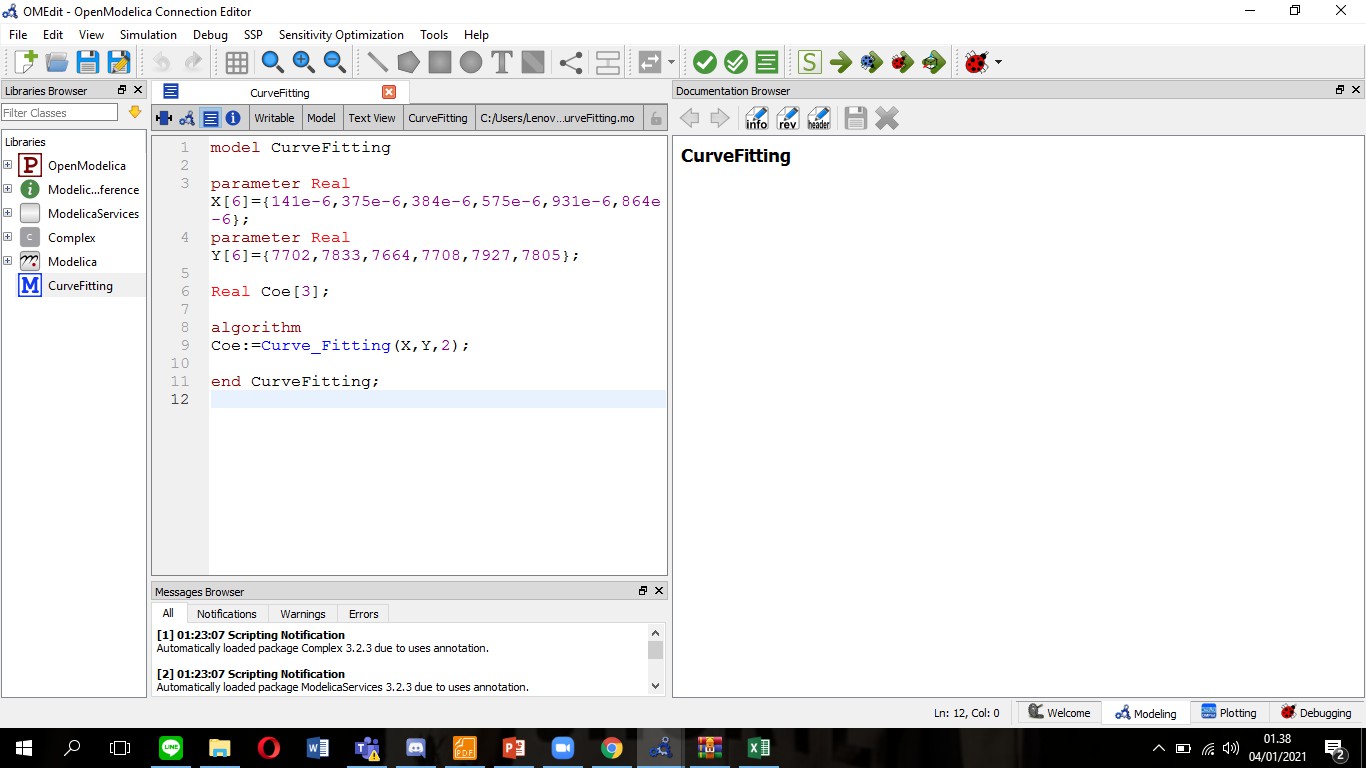
Untuk perhitungan curve fitting dengan model berikut :
model CurveFitting
parameter Real X[6]={141e-6,375e-6,384e-6,575e-6,931e-6,864e-6}; //area
parameter Real Y[6]={7702,7833,7664,7708,7927,7805}; // harga per kg
Real Coe[3];
algorithm Coe:=Curve_Fitting(X,Y,2);
end CurveFitting; model CurveFitting
dan curve fitting di rasio dan area dengan pemodelan berikut
//model CurveFitting
parameter Real X[6]={141e-6,375e-6,384e-6,575e-6,931e-6,864e-6}; //area
parameter Real Y[6]={7702,7833,7664,7708,7927,7805}; // ratio
Real Coe[3];
algorithm Coe:=Curve_Fitting(X,Y,2);
end CurveFitting;
lalu optimasi dengan golden rasio dengan program yang diajarkan oleh fahmi cristo dan josiah sebagai berikut
model optgold
parameter Real y [3]={1.06393e-24,-4.20893e-13,0.0416299};
parameter Real xlo=190e9;
parameter Real xhi=201e9;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end optgold;
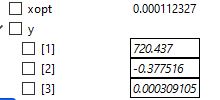
dari material lock menghasilkan xopt sebagai berikut:
maka dari hasil diatas yang paling optimal dari area ialah 20 x 20 x 3 mm
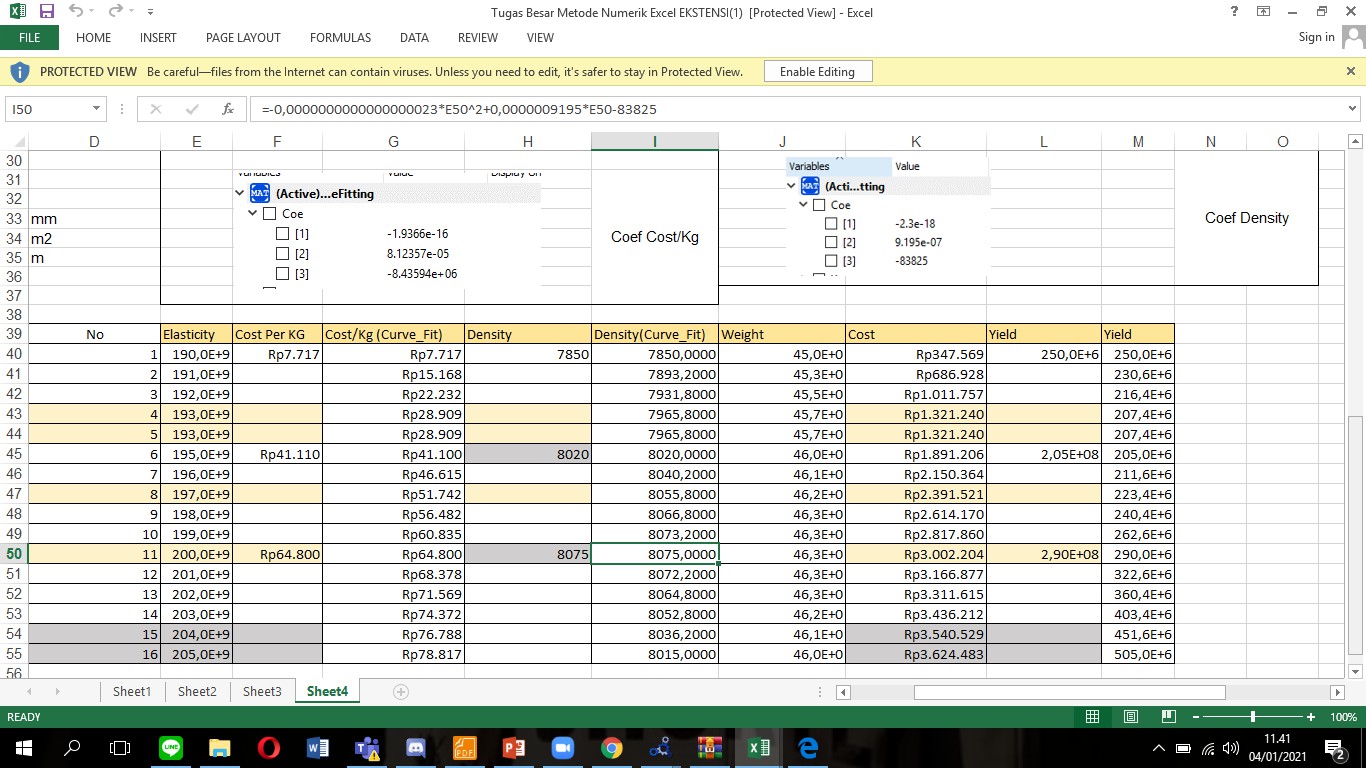
Pada excel yang kedua kita mengasumsikan dengan area yang sudah di optimasi sebesar 20 x 20 x 3 mm kita dapat mengasumsikan elastisitas dari material material yang kita pilih,disini saya menggunakan 3 material sebagai pembanding dalam perhitungan tersebut,berikut ialah excel area fix yang dibuat.
untuk perhitungan curve fitting di cost/kg,density dibandingkan dengan variabel bebas elastisitas dengan program berikut
//model CurveFitting
parameter Real X[6]={141e-6,375e-6,384e-6,575e-6,931e-6,864e-6}; //area
parameter Real Y[6]={7702,7833,7664,7708,7927,7805}; // ratio
Real Coe[3];
algorithm Coe:=Curve_Fitting(X,Y,2);
end CurveFitting;
lalu setelah mendapatkan curve fitting dari elastisitas dengan ratio kita dapat optimasi dengan golden rasio dengan program yang diajarkan oleh fahmi cristo dan josiah sebagai berikut:
model optgold
parameter Real y [3]={1.06393e-24,-4.20893e-13,0.0416299};
parameter Real xlo=190e9;
parameter Real xhi=201e9;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end optgold;
dari hasil optimasi didapatkan hasil sebagai berikut
maka dari hasil diatas yang paling optimal dari material yang dapat digunakan ialah ss400
UAS metode numerik
No. 7 model UAS
//define initial variable
parameter Integer Points = size(P, 1);
//Number of Points
parameter Integer Trusses = size(C, 1);
//Number of Trusses
parameter Real Yield = 214e6;
//Yield Strength (Pa)
parameter Real Area = 25;
//Area L Profile
parameter Real Elas = 68.9e9;
//Elasticity Al 6061 (Pa)
//define connection
parameter Integer C[:, 2] = [1, 2; 1, 3; 1, 4];
//define coordinates (please put orderly)
parameter Real P[:, 6] = [0, 0, 0, 1, 1, 1; //1
6.5, 6.5, 36.5, 1, 1, 1; //2
6.5, 6.5, 36.5, 1, 1, 1; //3
6.5, 6.5, 36.5, 1, 1, 1]; //4
//define external force (please put orderly)
parameter Real F[Points * 3] = {0,0,0,0,3708180,0,0,3708180,0,0,3708180,0};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N = 3 * Points; Real q1[3], q2[3], g[N, N], G[N, N], G_star[N, N], id[N, N] = identity(N), cx, cy, cz, L, X[3, 3]; Real err = 10e-10, ers = 10e-4;
algorithm
//Creating Global Matrix
G := id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Area * Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2];
g := zeros(N, N);
for m, n in 1:3 loop
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 1] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 2] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 1] - 1) + n] := -X[m, n];
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 2] - 1) + n] := -X[m, n];
end for;
G_star := G + g;
G := G_star;
end for;
//Solving Matrix //Transforming to global matrix //Implementing boundary
for x in 1:Points loop
if P[x, 4] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 2, a] := 0;
G[x * 3 - 2, x * 3 - 2] := 1;
end for;
end if;
if P[x, 5] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 1, a] := 0;
G[x * 3 - 1, x * 3 - 1] := 1;
end for;
end if;
if P[x, 6] <> 0 then
for a in 1:Points * 3 loop
G[x * 3, a] := 0;
G[x * 3, x * 3] := 1;
end for;
end if;
end for;
//Solving displacement
displacement := Modelica.Math.Matrices.solve(G, F);
//Solving reaction
reaction := G_star * displacement - F;
//Eliminating float error
for i in 1:N loop reaction[i] := if abs(reaction[i]) <= err then 0 else reaction[i]; displacement[i] := if abs(displacement[i]) <= err then 0 else displacement[i]; end for;
//Checking Force
check[1] := sum({reaction[i] for i in 1:3:N - 2}) + sum({F[i] for i in 1:3:N - 2});
check[2] := sum({reaction[i] for i in 2:3:N - 1}) + sum({F[i] for i in 2:3:N - 1});
check[3] := sum({reaction[i] for i in 3:3:N}) + sum({F[i] for i in 3:3:N});
for i in 1:3 loop
check[i] := if abs(check[i]) <= ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
dis[j] := abs(displacement[3 * (C[i, 1] - 1) + j] - displacement[3 * (C[i, 2] - 1) + j]);
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2];
Str := X * dis;
stress1[i] := Modelica.Math.Vectors.length(Str);
end for;
//Solving Matrix //Safety factor
for i in 1:Trusses loop
if stress1[i] > 0 then
safety[i] := Yield / stress1[i];
else
safety[i] := 0;
end if;
end for;
end UAS;