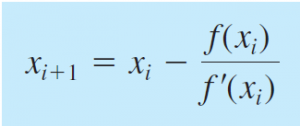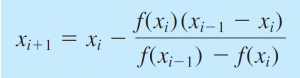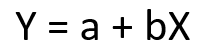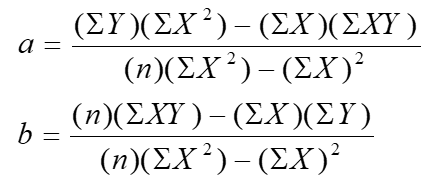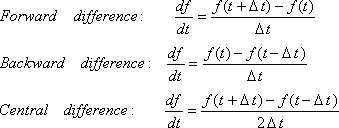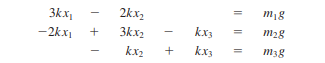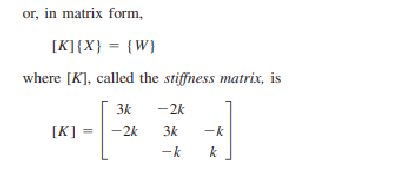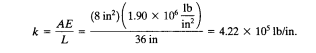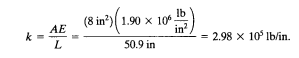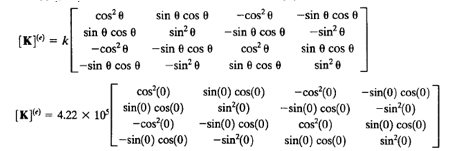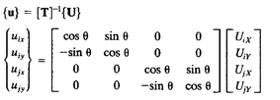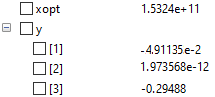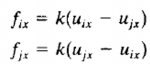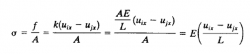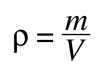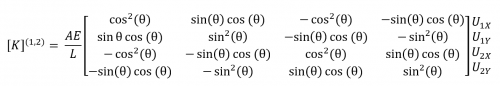Metnum03-Iza Azmar Aminudin
بِسْمِ اللّهِ الرَّحْمَنِ الرَّحِيْمِ
Assalamu'alaikum Wr. Wb,
Salam Sejahtera untuk kita semua,
Contents
[hide]- 1 Biodata Diri
- 2 Pendahuluan | Filosofi dalam Belajar Metode Numerik
- 3 Pertemuan 1: Review Materi Pra-UTS dan Pengantar Software Open-Modelica | 9 November 2020
- 4 Pertemuan 2: Review Tugas Modelica dan Simulasi Penyelesaian Metode Numerik | 16 November 2020
- 5 Pertemuan 3: Menyelesaikan Spring-mass System| 23 November 2020
- 6 Pertemuan 4: Membahas Penyelesaian Trusses dan Quis 1| 30 November 2020
- 7 Pertemuan 5: Menyelesaikan Persamaan Truss dengan Open Modelica untuk 2 dimensi dan 3 dimensi| 7 Desember 2020
- 8 Pertemuan 6: Muhasabah diri | 14 Desember 2020
- 9 Pertemuan 7: aplikasi metode numerik dalam kasus optimisasi | 21 Desember 2020
- 10 Sinopsis Tugas Besar: Mengoptimalkan Sistem Trusses untuk Mencapai Best Efficiency Point (BEP)
- 11 Pengerjaan Tugas Besar: Optimasi Sistem Trusses untuk Mencapai Best Efficiency Point (BEP)
- 12 UAS
- 12.1 1. Buatlah urutan langkah-langkah (prosedur) pemodelan numerik untuk optimasi struktur tersebut.
- 12.2 2. Jelaskan tujuan pemodelan numerik soal no 1 diatas, hukum/dalil (fisika) yang dipakai dan asumsi-asumsi yang akan digunakan dalam perhitungan
- 12.3 3. Untuk pemodelan numerik analisis strukturnya nya gunakan pendekatan 1D truss dgn membagi kolum (tiang) water tower kedalam 3 elemen (1D).
- 12.4 4. Susun urutan langkah-langkah (pseudocode) perhitungan matriks kesetimbangan global soal no 3 termasuk pengecekan kesalahan (verifikasi) perhitungannya
- 12.5 6. Tuliskan asumsi nilai-nilai parameter dan variable untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 elemnt 1 D diatas
- 12.6 7. Gunakan program modelica anda untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6
Biodata Diri
Perkenalkan saya:
Nama : Iza Azamr Aminudin
NPM : 1806233316
Kelas : Metnum-03
Melalui laman web ini, insya Allah saya akan berbagi kepada teman-teman sekalian terkait pembelajaran mata kuliah Metode Numerik yang saya pelajari bersama pa DAI dan teman-teman di kelas Metnum 03. Semoga yang saya tulis dalam laman ini dapat memberi hikmah bagi saya dan teman-teman pembaca, aamiiin.
Pendahuluan | Filosofi dalam Belajar Metode Numerik
Salah satu kewajiban hakiki untuk manusia adalah untuk belajar memetik hikmah dari semua pembelajaran yang akan terus ada selama hidup ini. Selain itu, Nabi Muhammad SAW sebagai idola saya pernah berkata bahwa sebaik-baiknya manusia adalah manusia yang paling bermanfaat bagi manusia (H.R Ahmad). Kedua hal ini insya Allah terus memotivasi saya untuk terus belajar dan memanfaatkan ilmu yang saya pelajari baik bagi kehidupan saya sendiri hingga untuk kepentingan orang banyak lainnya. Melalui mata kuliah metode numerik ini saya berharap untuk mendapatkan ilmu baik yang berupa materi pembelajaran seperti yang diajarkan oleh Pa DAI, dari buku, maupun melalui pengajaran yang dilakukan oleh asisten dosen dan teman-teman saya. Selain itu, saya berharap dengan menekuni pembelajaran metode numerik ini dapat menambah pengetahuan dan "ketidaktahuan" tentang hal-hal yang belum saya pelajari maupun mengerti sehingga terus menambah motivasi saya dalam belajar dan juga menjaga saya dari sikap riya dan takabur yang dapat membuat saya menjadi orang yang berpikiran tertutup dan menututp keran ilmu pengetahuan,
Semangat teman-teman semua dalam menimba ilmu dalam mata kuliah ini.
Dari ‘Abdullah bin ‘Amr dan Anas bin Malik radhiyallahu ‘anhuma, Rasulullah shallallahu ‘alaihi wa sallam bersabda,
قيِّدُوا العِلمَ بالكِتابِ
“Jagalah ilmu dengan menulis.” (Shahih Al-Jami’, no.4434. Syaikh Al-Albani mengatakan bahwa hadits ini sahih).
Pertemuan 1: Review Materi Pra-UTS dan Pengantar Software Open-Modelica | 9 November 2020
Review Materi Sebelum UTS
Pembelajaran mata kuliah Metode Numerik-03 sebelumnya diampu oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Selama pembelajaran sebelum UTS, kami mempelajari beberapa konsep yang digunakan dalam menyelesaikan permasalahan dengan metode numerik. Diantara materi-materi tersebut diantanya adalah sebagai berikut.
1. Deret Maclaurin dan Deret Taylor
Teorema Ketunggalan Andaikan f memenuhi uraian berikut,
f(x) = c0 + c1(x - a) + c2(x - a)^2 + c3(x - a)^3 . . .
untuk semua x dalam selang di sekitar a, maka cn = Jadi suatu fungsi tidak dapat digambarkan oleh dua deret pangkat dari (x - a).
2. Gauss Elimination
Metode ini menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut. Persamaan untuk Newton-Raphson adalah sebagai berikut:
4. Secant Method
Metode ini merupakan metode modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan). Persaman untuk metode Secant adalah sebagai berikut
|}
5. Regresi Linier
regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear.
Persamaan umum Regresi Linier adalah sebagai berikut:
dimana:
6. Turunan Numerik
Turunan Numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menghitung turunan numerik:
Tutorial Open-Modelica
https://www.youtube.com/watch?v=l7I8YlQBdug
Pertemuan 2: Review Tugas Modelica dan Simulasi Penyelesaian Metode Numerik | 16 November 2020
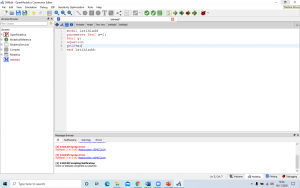
Pada kesempatan kali ini, kami mempelajari cara membuat program sederhana didalam modelica untuk menjumlahkan angka 10 kepada sebuah variable dan mencari rata-rata nilai dengan menggunakan software modelica.
1. Membuat program sederhana didalam modelica untuk menjumlahkan angka 10 kepada sebuah variable software modelica.
2. Mencari rata-rata nilai dengan menggunakan software modelica.
3. Tugas 02
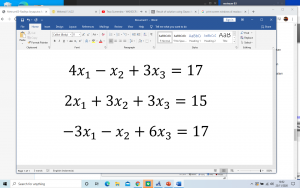
Melakukan Eliminasi Gauss untuk menyelesaikan persamaan linear tiga variabel. Tugas kali ini yaitu Pr2 metnum ... Buat class dengan type function untuk menyelesaikan persamaa2n aljabar simultan (metoda gauss elim, gauss seidel ataupun metoda lain) ... Dan sebuah class untuk menjalankan fungsi tersebut. Waktu 1 minggu dan dikumpulkan di wikipage air.eng.
Berikut adalah persamaan yang akan saya uji
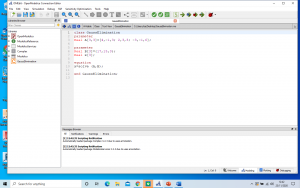
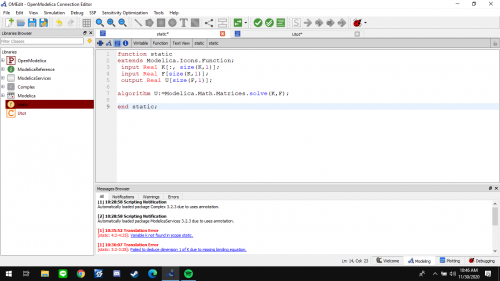
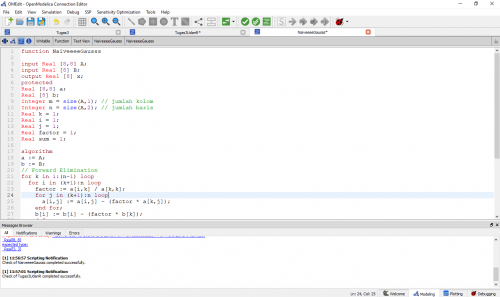
Kemudian saya membuat class sebagai berikut.
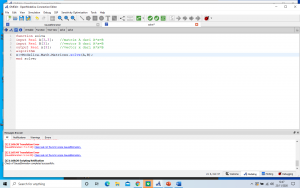
Dan membuat function sebagai berikut
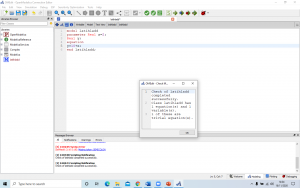
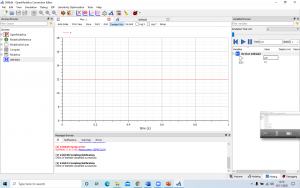
Setelah function dan class dibuat, barulah saya melakukan simulasi untuk mendapatkan hasilnya. Berikut adalah hasil yang saya dapatkan.
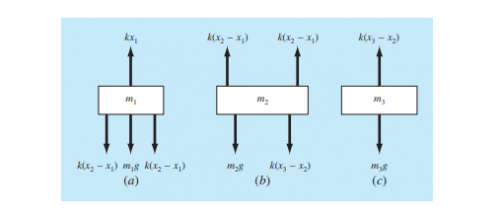
Pertemuan 3: Menyelesaikan Spring-mass System| 23 November 2020
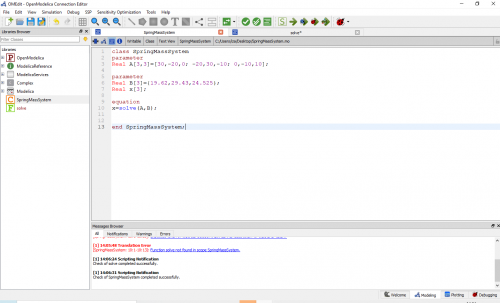
Menyelesaikan persamaan Spring-mass System dengan menggunakan software modelica
Nilai Delta x dapat dicari dari matriks tersebut dengan eliminasi Gauss menggunakan software modelica.
Sehingga didapatlah hasil sebagai berikut.
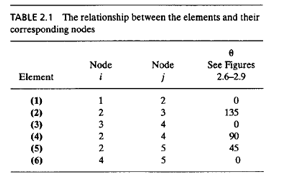
Tugas 3 Dalam tugas 3 kami diberikan suatu permasalahan metode numerik dalam suatu truses
Memisalkan trus dalam node-node
Berikut adalah persamaan
Matrix solusi dari trusses untuk diselesaikan dengan openmodelica
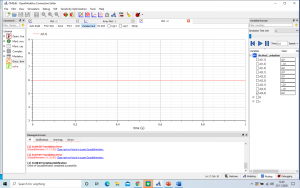
hasil grafik dan perhitungan dari modelica
Pertemuan 4: Membahas Penyelesaian Trusses dan Quis 1| 30 November 2020
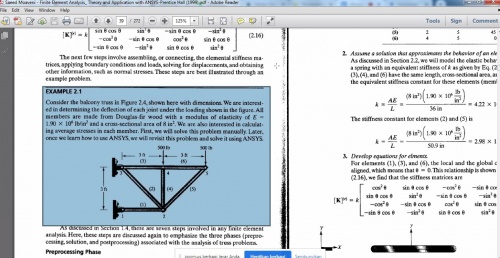
Soal Quis 1
Langkah-langkah dalam menyelesaikan soal
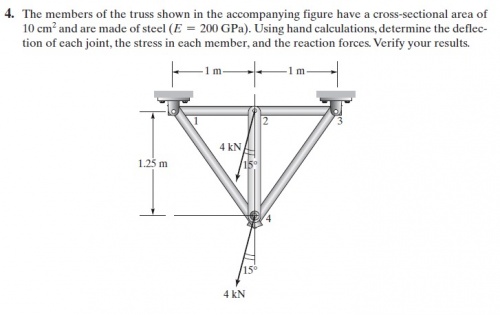
Menyelesaikan Soal no. 4
Proses mencari persamaan matriks untuk menentukan nilai konstanta kekakuan global
Setelah mendapatkan persamaan dari matriks untuk mencari kekakuan global dari masing-masing titik, langkah selanjutnya adalah dengan menggunakan perangkat lunak Open Modelica untuk mencari kekakuan global dari masing-masing titik tersebut
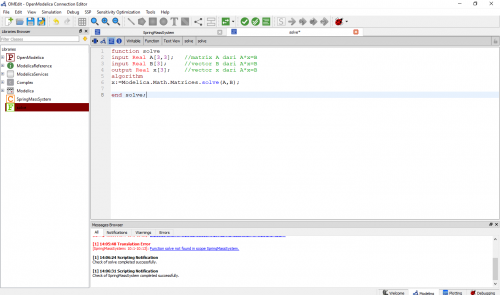
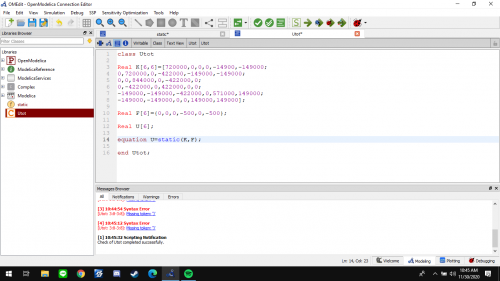
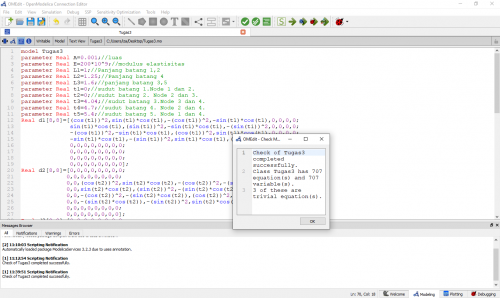
Berikut adalah Tampilan Coding di Software Modelica Beserta rincian Codingnya
Coding
Tampilan Modelica
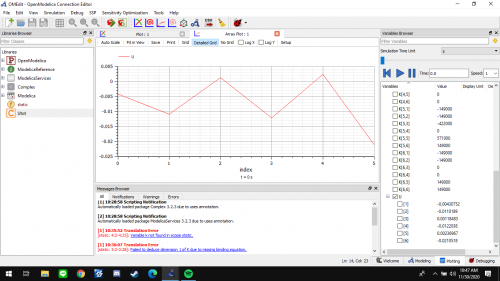
Selanjtnya dilakukan pengecekan Coding dan dilakukanlah simulasi
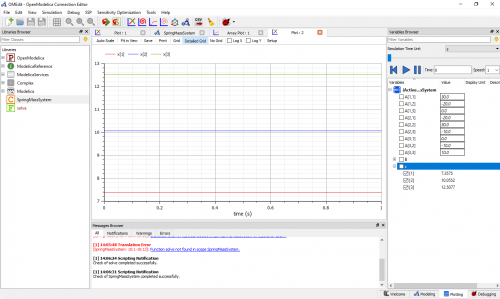
Berikut adalah hasil yang didapatkan dari simulasi menggunakan Open Modelica untuk mencari Kekakuan Lokal
Setelah itu, langkah selanjutnya adalah mencari displacement (U) dan reaction (R). Untuk mencari displacement, perlu diperhatikan boundary dan external load yang ada dan dimasukan kedalam matriks. Karena titik 1 dan 3 merupakan pinned, maka tidak ada displacement pada titik 1 dan 3(U1x=U1Y=U3X=U3Y=0). External load berada pada titik 2 dan 4 (pada arah x sebesar -4000Cos(15) sedangkan pada arah y sebesar 4000Cos(15)). Pada Open Modelica, menggunakan persamaan A*U=F dan R=(KG*U)-R untuk mencari displacement dan reaction setiap titik:
Berikut adalah coding yang digunakan untuk mencari displacement dan reaction. Dalam simulasinya, harus menggunakan NaiveGauss agar simulasi dapat dilakukan
Tampilan Modelica Untuk Coding Model U dan R serta function NaiveGauss
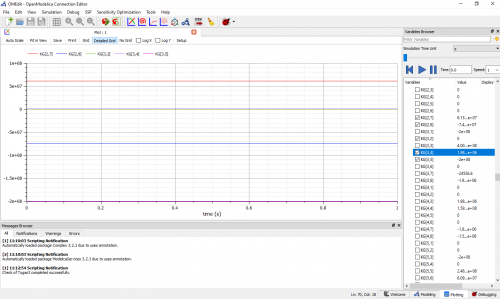
Berikut adalah hasil yang didapatkan
Pertemuan 5: Menyelesaikan Persamaan Truss dengan Open Modelica untuk 2 dimensi dan 3 dimensi| 7 Desember 2020
Terdapat beberapa cara yang dapat dilakukan untuk menyelesaikan suatu persoalan Truss dengan menggunakan Open Modelica. Pada pertemuan ini kami membahas tentang soal quiz yang telah diberikan pada pertemuan pekan 4. Jadi fungsi mempelajari soal ini adalah agar kita dapat lebih memahami pengaplikasian dari software openmodelica pada contoh kasus yang real. Pertemuan ini menjelaskan bagaimana alur pengerjaan soal quiz yang diberikan agar dapat membuat semua persamaan yang dapat digunakan pada kasus yang lebih umum.
Pada pertemuan ini, Pak Dai menunjuk ahmad muhammad fahmi untuk menjelaskan kepada teman-teman di kelas tentang fungsi-fungsi yang saya gunakan untuk mengerjakan soal quiz. Beberapa hal yang saya jelaskan antara lain:
1. Cara melakukan looping menggunakan fungsi for.
2. Cara membuat data dalam bentuk array.
3. Cara menggunakan fungsi if.
4. Apa itu floating number dan bagaimana cara menghilangkannya.
5. Apa itu protected variable.
6. Fungsi dari modelica class dengan specialization class dan function.
Tugas 5
Pertemuan 6: Muhasabah diri | 14 Desember 2020
Pada pertemua ini, kami diminta untuk menilai pemahaman diri kami sendiri untuk mata kuliah metode numerik. Kami diminta untuk mempresentasikan seberapa dalam pemahaman kami terkait materi metode numerik. Kami diminta untuk menjelaskan mengenai konsep fisika dari soal trusses yang selama ini kami garap. Lalu setelah itu, kami menjelaskan bagaimana cara untuk mensimulasikan soal trusses tersebut dalam perangkat openmodelica. Dalam soal kami mencari beberapa parameter seperti displacement lokal maupun global, konstanta stiffness lokal maupun global, serta reaction force yang dialami oleh tumpuan truss.
Dari kelas hari ini, saya mendapatkan beberapa bahan evaluasi yang perlu untuk saya perbaiki kedepannya. Pertama, jika dibandingkan dengan rekan-rekan sayan seperti ahmad muhammad fahmi, saya masih harus lebih banyak belajar lagi mengenai penggunaan openmodelica untuk mensimulasikan soal trusses ini. Kedepannya saya akan banyak berlatih dan mengeksplor lagi penggunaan openmodelica.
Pertemuan 7: aplikasi metode numerik dalam kasus optimisasi | 21 Desember 2020
Pada pertemuan kali ini kami mempelajari simulasi optimalisasi One-Dimensional Unconstrained menggunakan software openmodelica bersama dengan pa Dai dan ibu Candra. Kami mempelajari bagaimana cara mengaplikasikan perangkat openmodelica untuk mengoptimalkan suatu sistem trusses. Pada pertemuan ini kami mempelajari metode golden ratio untuk melakukan simulasi dalam suatu sistem.
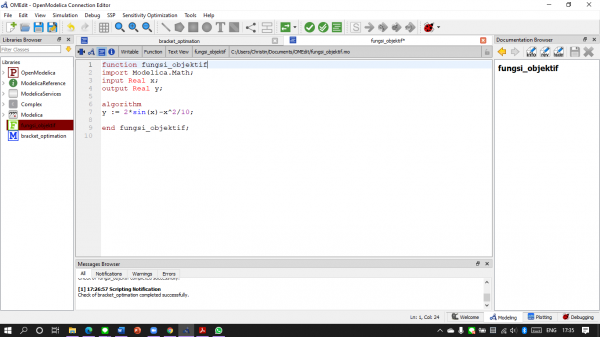
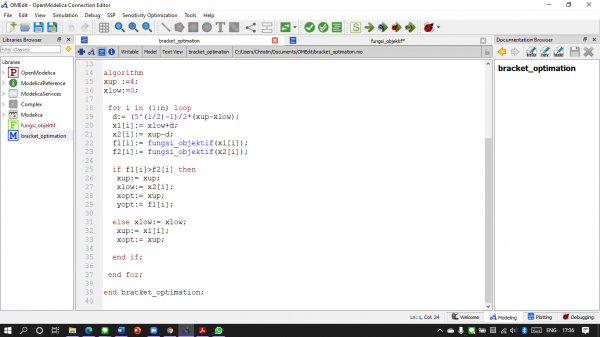
Fungsi yang digunakan adalah sebagai berikut :
Kelas pemanggilnya :
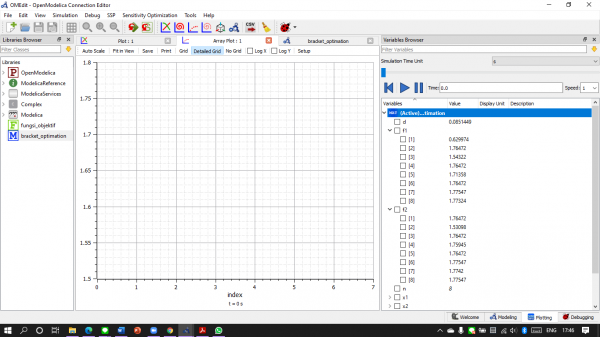
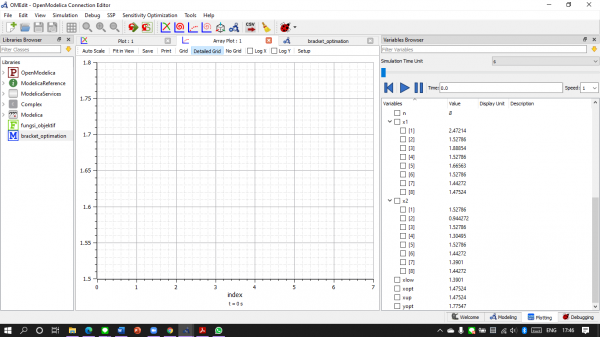
Sehingga didapatkan nilai :
Pada perhitungan, terdapat fungsi-fungsi batasan atau constraint seperti panjang siku ataupun harga per ukurannya. Optimasi mempunyai tujuan untuk meminimalisir biaya. Constrains yang diberikan adalah mampu menahan beban dimana gaya tersebut bekerja yang mampu didukung pada rangka tersebut. Langkah pertama adalah mencari displacement, memeriksa gaya, dan mengoptimasi gaya tersebut lalu menghitung stressnya. Setelah itu, membandingkan stress untuk kekuatan material yang akan digunakan. Tegangan yang dihitung tidak boleh melebihi allowable stress agar rangka sesuai standard nya. Dari data yang dikumpulkan, akan didapatkan jenis material serta ukuran batang dan spesifikasi siku. Setelah hal tersebut, dapat dilakukan optimasi untuk mendapatkan bahan yang paling optimal.
k = A.E/L
dimana :
A = Luas penampang siku
E = Modulus elastisitas tiap bahan
L = Panjang batang rangka
Bahan / profil siku yang akan digunakan merupakan galvanis, stainless, dan sebagainya.
Untuk pembahasan Aplikasi Metode Numerik dalam Kasus Optimasi, hal ini disampaikan oleh Bu Chandra dengan penjelasan optimasi yang digunakan merupakan metode bracket optimization using golden ratio. Bahan pembelajaran tersebut terdapat di PPT yang di share pada WA Group. Mahasiswa dihimbau untuk mengikuti simulasi menggunakan software OpenModelica untuk dapat menyelesaikan permasalahan terkait fungsi exercise yang diberikan.
Optimasi merupakan cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Optimasi fungsi non linear dan objektifnya merupakan cara untuk mencari nilai f(x) maksimum dan f(x) minimum. Berikut adalah persamaannya :
d = akar5 - 1/2 x (xu-xl)
x1 = x1 + d
x2 = xu . d
dengan syarat :
- f(x1) > f(x2), domain sebelah kiri x2 dapat dieliminasi xL = x2 untuk iterasi berikutnya xu = xu lama
- f(x2) > f(x1), domain x sebelah kanan x1 dapat dieliminasi xu = x1 untuk iterasi berikutnya xL = xL lama
Sinopsis Tugas Besar: Mengoptimalkan Sistem Trusses untuk Mencapai Best Efficiency Point (BEP)
Tugas Besar
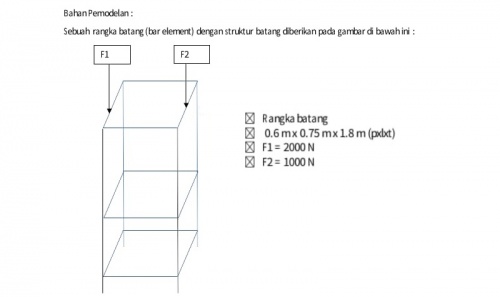
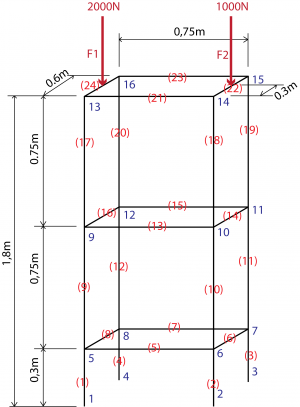
Pada tugas besar kali ini, kami diberi tugas untuk mengaplikasikan ilmu metode numerik untuk mengoptimasi suatu sistem trusses dengam menggunakan perangkat lunak openmodelica. Berikut adalah geometri rangka beserta parameter-parameternya.
Tugas kami adalah mencari Best Efficiency point untuk sistem trusses ini mengacu pada harga dan juga kemampuan fisik dari trusses itu sendiri. Dalam tugas besar kali ini, kami mengerjakan pembuatan coding tersebut secara bersama-sama dari 2 kelas metode numerik 02 dan 03 dengan dipimpin oleh Ahmad Muhammad fahmi, Josiah Enrico, dan juga Christoper.
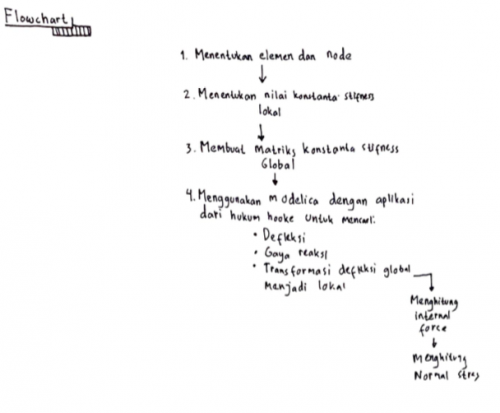
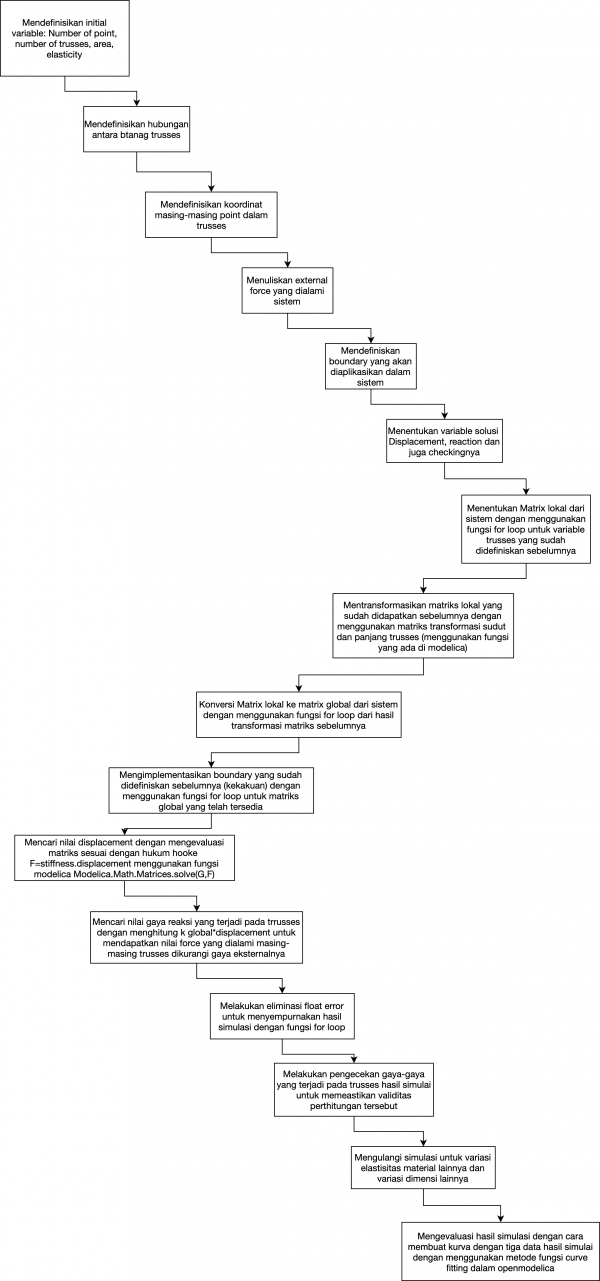
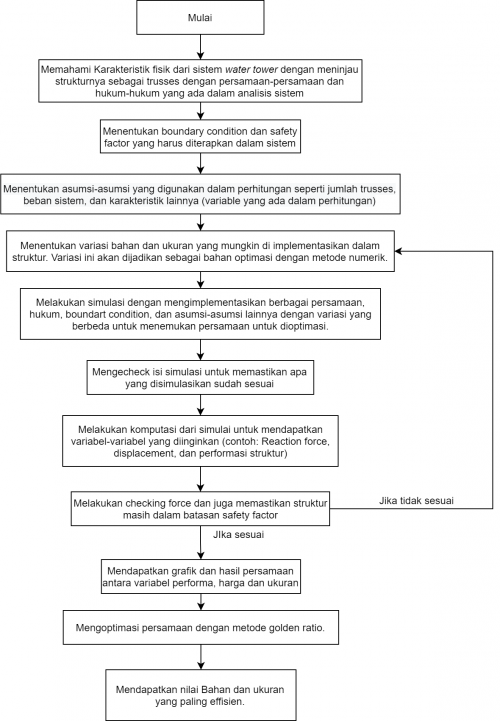
Flow Chart
Berikut adalah flow chart pengerjaan tugas besar dan pembuatan codinng untuk tugas besar
Pengerjaan Tugas Besar: Optimasi Sistem Trusses untuk Mencapai Best Efficiency Point (BEP)
Berikut adalah langkah-langkah yang telah dilakukan dalam mengerjakan tugas besar sesuai dengan flowchart yang telah dibuat sebelumnya.
1. Memahami karakteristik fisik trusses
Kasus kali ini, kami diberikan suatu bentuk trusses dengan 16 komponen penyusunnya (truss) dan terdapat 24 point dalam trusses tersebut. Trusses tersebut tersebut disusun secara hotizontal dan vertikal sehingga sudut yang dihasilkan dalam trusses hanya berbentuk 0 dan 90 derajat menurut pada sumbu x negatif. Kami diminta untuk membuat optimasi dari trusses ini berdasarkan pada harga serta kemampuan fisiknya. Governing Equation yang digunakan dalam sistem ini adalah dari formulasi finite element untuk defleksi sebagai berikut.
F=(AE/L)∆L
Dengan F adalah gaya yang dialami oleh trusses, A adalah luas penampang trusses, E adalah elastisitas bahan, L adalah panjang trusses dan ∆L adalah pertambahan panjang.
Selain itu, untuk mengevaluasi perhitungan , kami menggunakan hukum hooke untuk mengetahui hubungan antara stiffness trusses dengan gaya-gaya yang terjadi dalam trusses. Persamaan dasarnya adalah sebagai berikut.
k=AE/L
Dengan k adalah konstanta kekakuan.
Nantinya, trusses ini akan diselesaikan dengan metode numerik dengan bentuk matriks yang memiliki persamaan dasar untuk dislacement sebagai berikut sebagai berikut.
{U}=[T]{u}
dengan U adalah displacement dari perspektif global, dan u adalah displacement untuk perspektif lokal serta T adalah matriks transformasi.
Sementara hubungan antara nilai force yang dialam trusses antara lokal dan global dihubungkan dengan persamaan berikut.
{F}=[T]{f}
dengan F adalah force yang terjadi pada node dari perspektif global, dan f adalah force yang dialami node untuk perspektif lokal serta T adalah matriks transformasi.
Persamaan tersebut dielaborasikan menjadi persamaan sebagai berikut
{F}=[T][K][T]⁻¹{U}
2. Mendefinisikan Asumsi dalam Perhitungan
Asumsi yang digunakan untuk melakukan perhitungan ini antara lain:
- Beban akan terdistribusi hanya pada node (karena bersifat trusses).
- Safety factor minimal bernilai 2.
- Batas displacement 0,001 m sebelum buckling (pada truss paling atas).
- Ketinggian trusses pada tiap lantai sama yaitu 0,6 m.
- tidak ada bending karena bersifat truss
- Beban terdistribusi pada node
Metodologi
A. Untuk jenis material yang sama:
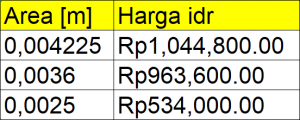
1. Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu ASTM A36. 2. Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal. 3. Membuat rasio antara safety factor dengan harga total. 4. Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting. 5. Melakukan optimasi menggunakan metode golden section.
B. Untuk area penampang yang sama:
1. Mencari harga untuk 3 jenis material dengan area penampang yang sama yaitu 171 mm^2. 2. Mengitung nilai safety factor pada 3 jenis batang dengan coding awal. 3. Membuat rasio antara safety factor dengan harga total. 4. Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting. 5. Melakukan optimasi menggunakan metode golden section.
3. Mendefinisikan bagian-bagian dalam trusses
Constraint
- Node 1,2,3,4 (lantai dasar) fixed
- Beban F1 dan F2 terdistribusi ke node sekitaranya, sehingga:
1. Node 13 & 16 = 1000N
2. Node 14 & 15 = 500N
4. Menentukan variasi material dan variasi luas penampang untuk menghitung optimasi
Berikut adalah beberapa variasi yang dilakukan dalam melakukan optimasi.
Material tetap, variasi luas permukaan
Luas penampang tetap, variasi material
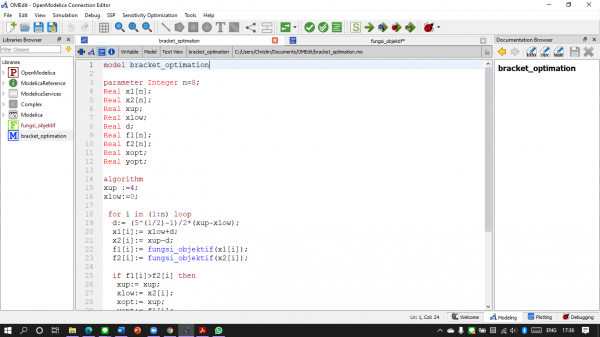
5. Membuat Codingan untuk Mencari nilai displacement, reaction force, dan melakukan optimasi
Berikut adalah coding hasil diskusi dua kelas yang dipimpin oleh Josiah, Fahmi, dan Christo
- Untuk perhitungan displacement, reaction force, stress, dan safety factor:
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
- Untuk membuat kurva curve fitting:
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
- Untuk golden section:
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
6. Hasil Perhitungan
Setelah melakukan simulasi dengan menggunakan openmodelica dan dengan optimasi menggunakan metode golden ratio, berikut adalah hasilnya.
- Nilai rasio dari safety factor dengan harga
Luas penampang tetap, variasi material
- Nilai luas area penampang optimum untuk material SS201 adalah 283,81 mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 6m dan tebal 60mm.
- Material optimum yang dapat digunakan untuk luas penampang 360mm^2 adalah material dengan nilai elastisitas 15324000000000 N/m^2 atau material yang paling mendekati adalah SS316L.
UAS
بِسْمِ اللّهِ الرَّحْمَنِ الرَّحِيْمِ
Nama : Iza Azmar Aminudin
NPM : 1806233316
Kelas : Metode Numerik-03
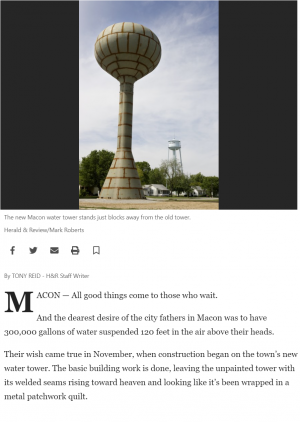
Pada kesempatan kali ini, saya akan berbagi mengenai pengerjaan Ujian Akhir Semester mata kuliah Metode Numerik yang telah dilaksanakan pada 13 Januari 2021. Berikut adalah soal, jawaban, dan pembahasan dari Ujian Akhir Semester Metode Numerik. Selamat membaca.
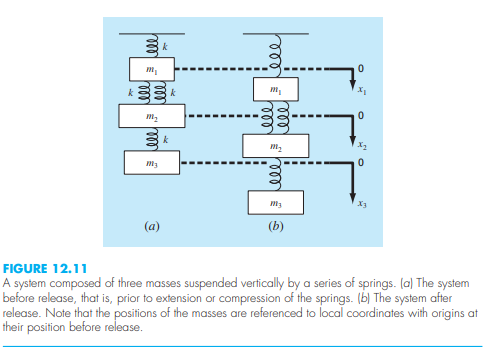
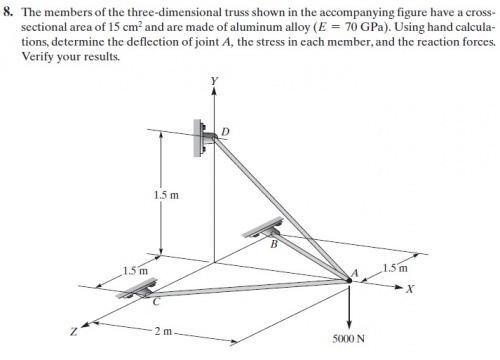
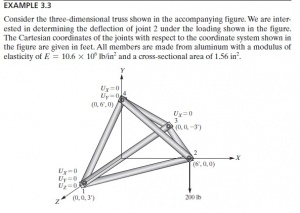
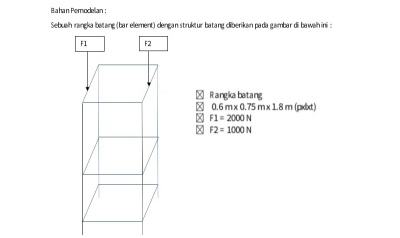
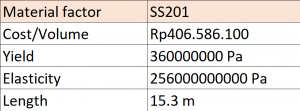
Perhatikan Water Tower dengan Reservoir berbentuk Bola pada Gambar diatas! Anda diminta untuk membuat pemodelan numerik untuk mengoptimalkan struktur Water Tower tersebut.
1. Buatlah urutan langkah-langkah (prosedur) pemodelan numerik untuk optimasi struktur tersebut.
Pada soal ini, kami diinstruksikan untuk membuat langkah-langkah dalam membuat pemodelan numerik untuk optimasi struktur ini. Untuk mempermudah pemodelan, struktur water tower ini dianggap sebagai struktur trusses. Pemodelan yang diharapkan adalah untuk mendapatkan titik efisiensi terbaik dengan mempertimbang harga bahan, ukuran, dan performansi dari struktur. Berikut adalah langkah-langkah pemodelan numerik untuk optimasi struktur water tower ini.
Jawaban saat UAS
2. Jelaskan tujuan pemodelan numerik soal no 1 diatas, hukum/dalil (fisika) yang dipakai dan asumsi-asumsi yang akan digunakan dalam perhitungan
A. Tujuan:
Untuk menentukan ukuran dan jenis bahan yang paling optimum (titik efisiensi terbaik) untuk di implementasikan dalam sistem dengan mempertimbangkan kebutuhan dan keamanan dari struktur water tower tersebut.
B. Hukum/dalil yang digunakan dalam perhitungan:
| Persamaan | Hukum/Dalil | Keterangan |
| Hukum Hooke | Dimana F adalah gaya, k adalah konstanta kekakuan, dan x adalah defleksi. Dari hukum ini kita dapat mendapatkan nilai konstanta stiffness dari sistem, serta displacemet yang terjadi pada masing-masing komponen trusses. | |
| Internal Force | Dimana fix dan fjx adalah gaya internal pada member yang ditinjau pada node i dan j. | |
| Normal Stress | Dimana σ adalah normal stress pada komponen trusses. Perhitungan ini dapat digunakan nanti untuk menghitung stress yang menjadi beban bagi struktur | |
| Hukum Konservasi massa | Hukum konservasi massa dipakai untuk memperkirakan beban yang ditanggung oleh struktur dari air yang ditampungnya | |
C. Asumsi yang digunakan:
1. Struktur ditinjau sebagai sebuah trusses
2. Beban struktur dari material yang dipakai tidak dijadikan pertimbangan perhitungan
3. Beban terdistribusi pada ujung-ujung trusses (point)
4. Struktur mengalami perubahan secara statis dan tidak dipengaruhi waktu
Jawaban saat UAS
3. Untuk pemodelan numerik analisis strukturnya nya gunakan pendekatan 1D truss dgn membagi kolum (tiang) water tower kedalam 3 elemen (1D).
a). Susunlah persamaan aljabar kesetimbangan statik setiap elemen tsb. (matriks kesetimbangan lokal) Berikut adalah rumusn mencari rumusan matriks lokal pada struktur trusses water tower ini.
Sistem dianggap sebagai trusses dengan 3 kolom (tiang) diasumsikan nantinya ketiga trusses ini akan dianalisis untuk mencari kekakuannya dengan menggunakan matriks lokalnya terlebih dahulu. Setelah didapatkan stifness lokalnya, nantinya hasilnya akan dimasukan dalam perhitungan matriks global untuk mencari kekakuan global.
b) Matriks kesetimbangan global
Berikut adalah rumusan matriks globalnya.
Jawaban saat UAS
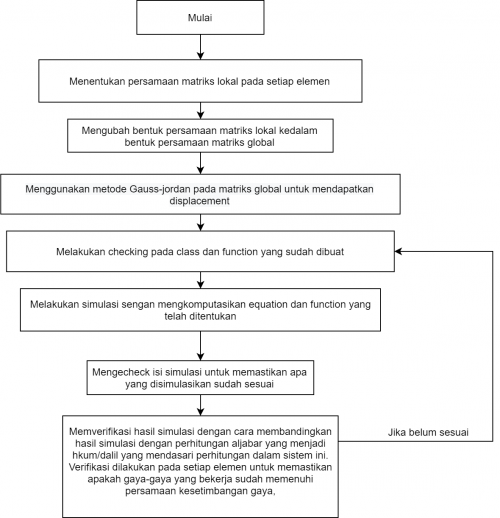
4. Susun urutan langkah-langkah (pseudocode) perhitungan matriks kesetimbangan global soal no 3 termasuk pengecekan kesalahan (verifikasi) perhitungannya
Berikut adalah flowchart dari langkah-langkah menghitung matriks kesetimbangan global.
Jawaban saat UAS
6. Tuliskan asumsi nilai-nilai parameter dan variable untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 elemnt 1 D diatas
Berikut adalah asumsi nilai-nilai parameter dan variable yang akan digunakan dalam iterasi
7. Gunakan program modelica anda untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6
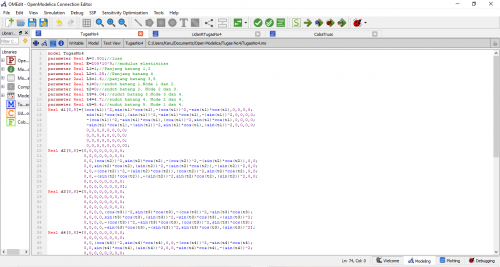
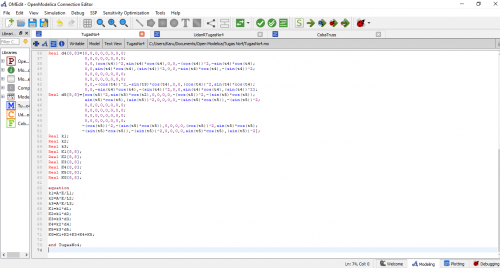
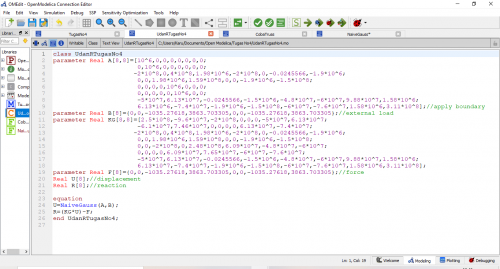
- Coding untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6
model UASMetnum
/*Iza Azmar Aminudin
1806181773 */
parameter Real P[3]={10000,0,-10000};//beban dan gaya reaksi
/*data-data asumsi dan elemen sejenis*/
parameter Real a=10e-4;//area
parameter Real e=35e9;//elastisitas
parameter Real m=36.576;//panjang elemen
/*parameter yang dicari*/
Real k;//stiffness elemen
Real kg[3,3];//matriks global elemen
Real u[3];//displacement
Real stress[3];//stress elemen
algorithm
/*nilai kekakuan*/
k := a*e/m;
/*persamaan matriks global*/
kg := [ k,2*k, 0;
-k,2*k,-k;
0,-k,2*k];
/*displacement dengan metode Gauss-Jordan*/
u := Modelica.Math.Matrices.solve(kg,P);
/*stress pada tiap elemen*/
stress[1] := u[1]*k/a;
stress[2] := u[2]*k/a;
stress[3] := u[3]*k/a;
end UASMetnum;
- Hasil Simulasi
Selesai