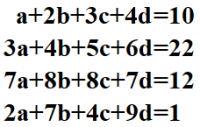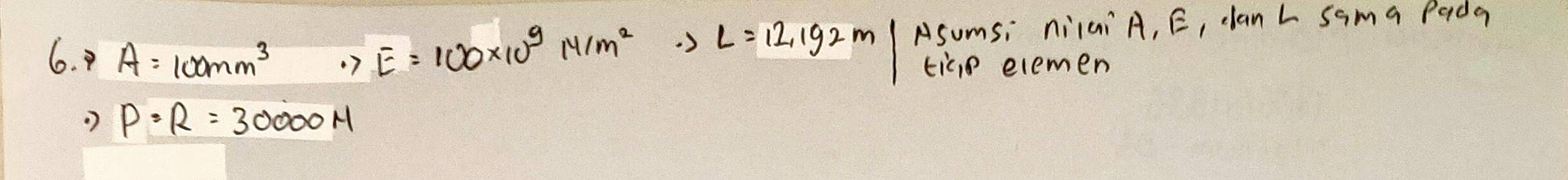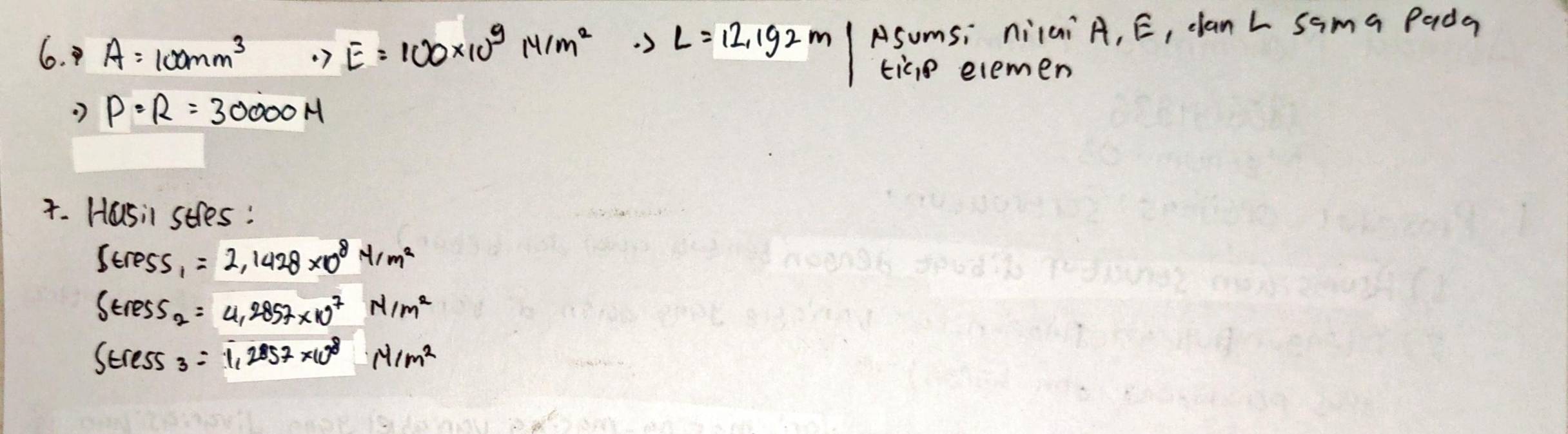Metnum03-Ahmad Mohammad Fahmi
Contents
BIODATA
Nama : Ahmad Mohammad Fahmi
NPM : 1806181836
Kelas : Metoda Numerik - 03
Materi Sebelum UTS
1. Deret Maclaurin
Deret maclaurin digunakan untuk memudahkan mencari nilai akar persamaan yang nilainya tidak bulat.
2. Turunan Numerik
Sebuah fungsi yang digunakan untuk mencari nilai turunan dari sebuah persamaan secara numerik yang asal rumusnya berasal dari deret maclaurin.
3. Metode pencarian akar
Metode Bracket
Pada metode ini, pemilihan dua angka yang akan menjadi nilai inisiasi dari perhitungan harus mengapit nilai akar yang dicari. Salah satu metode yang diajarkan oleh pak engkos adalah metode Bisection.
Metode Open
Pada metode ini, pemilihan angka yang akan menjadi nilai inisiasi dari perhitungan tidak harus mengapit nilai akar yang dicari. Metode yang diajarkan oleh pak engkos adalah metode Newton Rhapson dan Secant.
4. Pencocokan Kurva
Metode pencocokan kurva dapat dilakukan dengan melakukan regresi linear.
PERTEMUAN 1
Tugas 1
Pada tugas ini, saya coba mempelajari cara membuat simulasi feedback yang menggunakan sistem PID melalui video berikut:
https://www.youtube.com/watch?v=Dw66ODbMS2A
PERTEMUAN 2
Pada pertemuan ini, kami diajarkan bagaimana cara melakukan perhitungan menggunakan openmodelica.
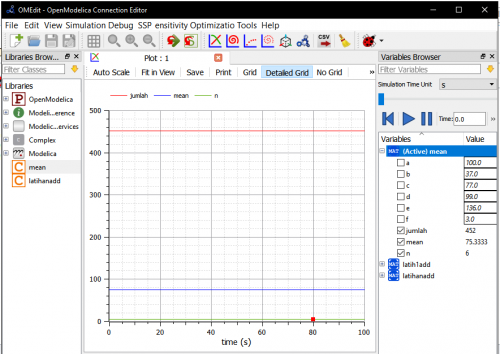
Kami diberikan tugas untuk melakukan perhitungan rata-rata dari beberapa data. Berikut ini adalah hasil dari perhitungan saya:
Selain menghitung rata-rata, saya juga mencoba melakukan perhitungan sederhana sebagai berikut:
Tugas 2
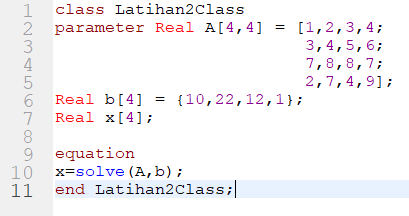
Pada tugas ini, saya mencoba menyelesaikan persamaan-persamaan berikut:
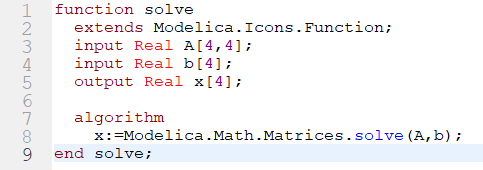
Untuk mencari nilai variabel dari persamaan-persamaan tersebut, saya coba menyelesaikannya dengan menggunakan metode eliminasi gauss dengan sumber referensi https://build.openmodelica.org/Documentation/Modelica.Math.Matrices.solve.html
Berikut adalah hasil dari percobaan saya:
Pada bagian function:
Pada bagian class:
Hasil perhitungan:
Dari hasil perhitungan didapat nilai variabel a=20.9375, b=-18.8125, c=-11.1875, dan d=15,0625
Pertemuan 3
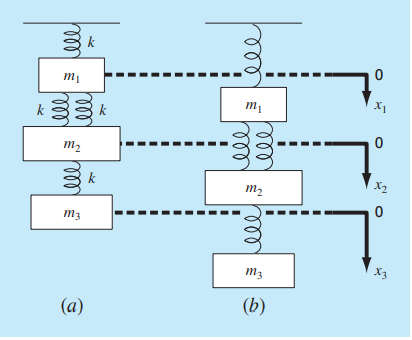
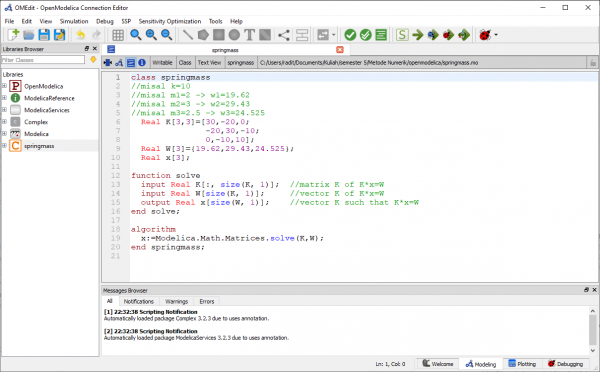
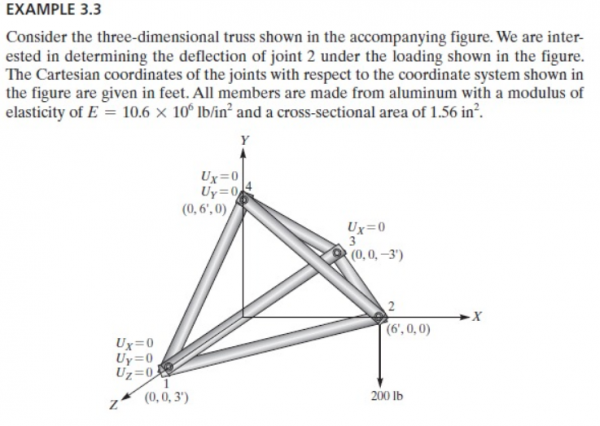
Pada pertemuan ini, kami diminta untuk mencoba mengerjakan soal dari buku Metode Numerik edisi ke 7 karangan Steven C.Chapra dan Raymond P.Canel pada hal 328 latihan 12.11.
Pada open modelica, saya menggunakan coding sebagai berikut:
Hail yang didapat adalah sebagai berikut:
TUGAS 3
Pada tugas ini kami diminta untuk menghitung defleksi pada setiap batang dan gaya reaksinya.
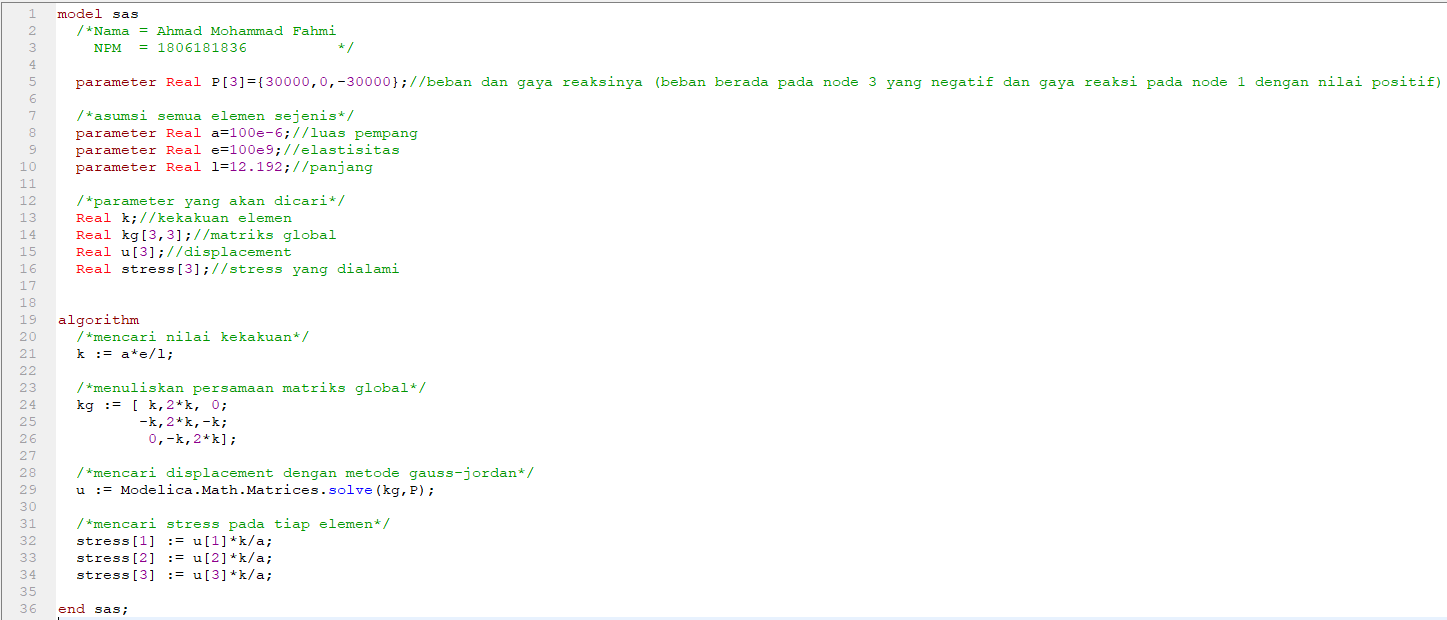
Coding yang saya guanakan untuk soal ini adalah sebagai kerikut:
- Class
|
Fungsi Utama class QuizSoal1
parameter Real [:,7] inisiasi = [1, 1, 2, 0, 8, 1.9e6, 36.00;
2, 2, 3, 135.00, 8, 1.9e6, 50.90;
3, 3, 4, 0, 8, 1.9e6, 36.00;
4, 2, 4, 90.00, 8, 1.9e6, 36.00;
5, 2, 5, 45.00, 8, 1.9e6, 50.90;
6, 4, 5, 0, 8, 1.9e6, 36.00];
parameter Integer [:,2] node = [1, 2;
2, 3;
3, 4;
2, 4;
2, 5;
4, 5];
parameter Integer y = size(node,1);
parameter Integer x = 2*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {1,3};
parameter Real [:,3] node_load = [1, 0, 0;
2, 0, -0;
3, 0, 0;
4, 0, -500;
5, 0, -500];
parameter Real [2*(size(node_load,1))] load = {0,0,0,0,0,0,0,-500,0,-500};
Real [y] k;
Real [y,4,4] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
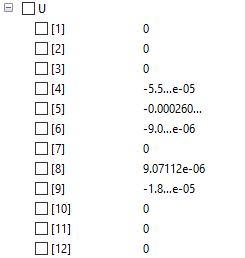
Real [x] U;
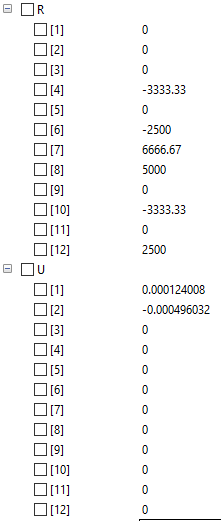
Real [x] R;
equation
k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(node, x, y, Ke); KgTot = SumStiffnessMatrixGlobal(x, y, Kg); KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); U = GaussJordan(x, KgB, load); R = ReactionForce(x, KgTot, U, load); end QuizSoal1; |
- Function
|
Stiffness Matrix Element function StiffnessMatrixElement input Real [:,7] inisiasi_mat; output Real [size(inisiasi_mat,1),4,4] Ke_mat; protected Real theta; Real [3] StiffTrig; Real [4,4] StiffTrans; Real [size(inisiasi_mat,1)] k_vec; Real float_error = 10e-10; algorithm
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / inisiasi_mat[i,7]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member for i in 1:size(inisiasi_mat,1) loop // Clearing the matrices StiffTrig := zeros(3); StiffTrans := zeros(4,4); // Converting degrees to radians theta := Modelica.SIunits.Conversions.from_deg(inisiasi_mat[i,4]); // {cos^2, sin^2, sincos}
StiffTrig := {(Modelica.Math.cos(theta))^2,
(Modelica.Math.sin(theta))^2,
(Modelica.Math.sin(theta)*Modelica.Math.cos(theta))};
// Handle float error elements in StiffTrig
for t in 1:size(StiffTrig,1) loop
if abs(StiffTrig[t]) <= float_error then
StiffTrig[t] := 0;
end if;
end for;
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[3], -1*StiffTrig[1], -1*StiffTrig[3];
StiffTrig[3], StiffTrig[2], -1*StiffTrig[3], -1*StiffTrig[2];
-1*StiffTrig[1], -1*StiffTrig[3], StiffTrig[1], StiffTrig[3];
-1*StiffTrig[3], -1*StiffTrig[2], StiffTrig[3], StiffTrig[2]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:4 loop
for n in 1:4 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for; end StiffnessMatrixElement; |
|
Stiffness Matrix Global function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,4,4] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop Kg_mat[i,2*n[i,1],2*n[i,1]]:=Ke_mat[i,2,2]; Kg_mat[i,2*n[i,1]-1,2*n[i,1]-1]:=Ke_mat[i,1,1]; Kg_mat[i,2*n[i,1],2*n[i,1]-1]:=Ke_mat[i,2,1]; Kg_mat[i,2*n[i,1]-1,2*n[i,1]]:=Ke_mat[i,1,2]; Kg_mat[i,2*n[i,2],2*n[i,2]]:=Ke_mat[i,4,4]; Kg_mat[i,2*n[i,2]-1,2*n[i,2]-1]:=Ke_mat[i,3,3]; Kg_mat[i,2*n[i,2],2*n[i,2]-1]:=Ke_mat[i,4,3]; Kg_mat[i,2*n[i,2]-1,2*n[i,2]]:=Ke_mat[i,3,4]; Kg_mat[i,2*n[i,2],2*n[i,1]]:=Ke_mat[i,4,2]; Kg_mat[i,2*n[i,2]-1,2*n[i,1]-1]:=Ke_mat[i,3,1]; Kg_mat[i,2*n[i,2],2*n[i,1]-1]:=Ke_mat[i,4,1]; Kg_mat[i,2*n[i,2]-1,2*n[i,1]]:=Ke_mat[i,3,2]; Kg_mat[i,2*n[i,1],2*n[i,2]]:=Ke_mat[i,2,4]; Kg_mat[i,2*n[i,1]-1,2*n[i,2]-1]:=Ke_mat[i,1,3]; Kg_mat[i,2*n[i,1],2*n[i,2]-1]:=Ke_mat[i,2,3]; Kg_mat[i,2*n[i,1]-1,2*n[i,2]]:=Ke_mat[i,1,4]; end for; end StiffnessMatrixGlobal; |
|
Sum of Stiffness Matrix Global function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal; |
|
Implement Boundary Condition function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:1 loop
KgB_met[2*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:1 loop
KgB_met[2*Boundary_met[a]-b,z*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
|
|
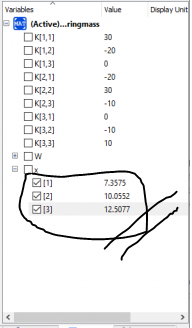
Gauss-Jordan function GaussJordan input Integer x; input Real [x,x] KgB_met; input Real [x] load_met; output Real [x] U_met; Real float_error = 10e-10; algorithm U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan; |
|
Reaction Force function ReactionForce input Integer x; input Real [x,x] KgTot_met; input Real [x] U_met; input Real [x] load_met; output Real [x] R_met; algorithm R_met := (KgTot_met*U_met)-load_met; end ReactionForce; |
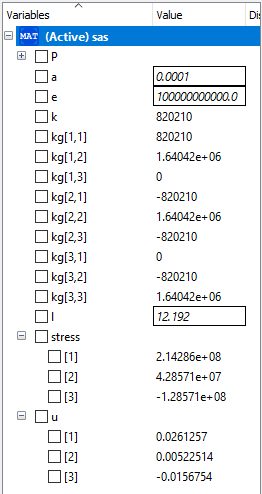
Hasil yang didapat adalah sebagai berikut:
Berikut link untuk mendownload file yang saya gunakan:
https://drive.google.com/drive/folders/1XSDTQOP8a5lig-JMByNTwxOiMWsp_qe8?usp=sharing
PERTEMUAN 4
Membahas tentang pembebeanan statik dan dinamik serta hubungan statika struktur dengan metode numerik.
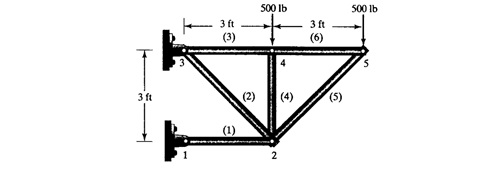
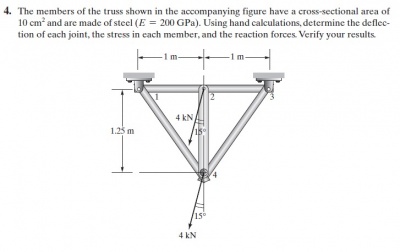
QUIZ
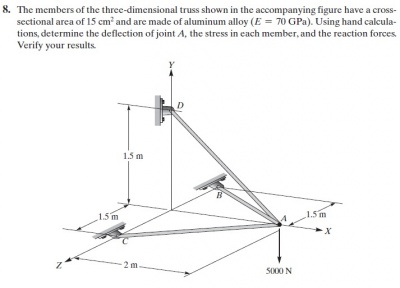
Pada quiz ini kami diminta mencari defleksi dan gaya reaksi pada struktur berikut.
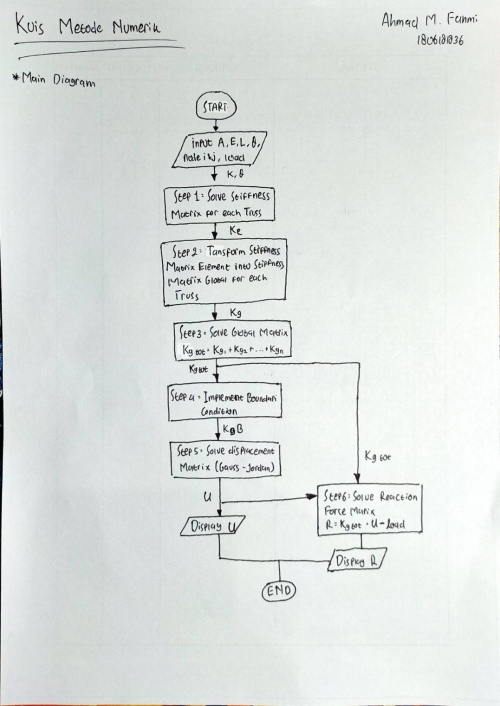
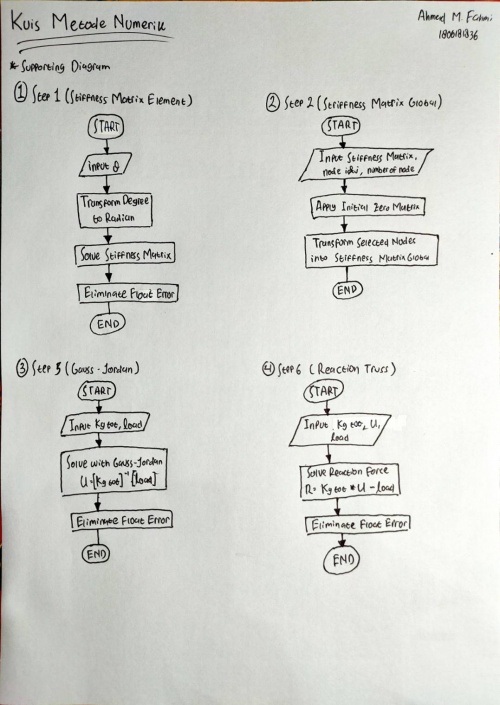
Pertama kami diminta untuk membuat flowchart untuk proses pengerjaan soal. Flowchart yang digunakan untuk kedua soal ini sama, yaitu:
Untuk menyelesaikan soal no.4 saya menggunakan coding berikut:
- Class
|
Fungsi Utama class QuizSoal1
parameter Real [:,7] inisiasi = [1, 1, 2, 0, 10e-4, 200e9, 1.00;
2, 2, 3, 0, 10e-4, 200e9, 1.00;
3, 1, 4, 308.66, 10e-4, 200e9, 1.60;
4, 2, 4, 270.00, 10e-4, 200e9, 1.25;
5, 3, 4, 231.34, 10e-4, 200e9, 1.60];
parameter Integer [:,2] node = [1, 2;
2, 3;
1, 4;
2, 4;
3, 4];
parameter Integer y = size(node,1);
parameter Integer x = 2*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {1,3};
parameter Real [:,3] node_load = [1, 0, 0;
2, -1035.28, -3863.70;
3, 0, 0;
4, -1035.28, -3863.70];
parameter Real [2*(size(node_load,1))] load = {0,0,-1035.28,-3863.70,0,0,-1035.28,-3863.70};
Real [y] k;
Real [y,4,4] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(node, x, y, Ke); KgTot = SumStiffnessMatrixGlobal(x, y, Kg); KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); U = GaussJordan(x, KgB, load); R = ReactionForce(x, KgTot, U, load); end QuizSoal1; |
- Function
|
Stiffness Matrix Element function StiffnessMatrixElement input Real [:,7] inisiasi_mat; output Real [size(inisiasi_mat,1),4,4] Ke_mat; protected Real theta; Real [3] StiffTrig; Real [4,4] StiffTrans; Real [size(inisiasi_mat,1)] k_vec; Real float_error = 10e-10; algorithm
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / inisiasi_mat[i,7]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member for i in 1:size(inisiasi_mat,1) loop // Clearing the matrices StiffTrig := zeros(3); StiffTrans := zeros(4,4); // Converting degrees to radians theta := Modelica.SIunits.Conversions.from_deg(inisiasi_mat[i,4]); // {cos^2, sin^2, sincos}
StiffTrig := {(Modelica.Math.cos(theta))^2,
(Modelica.Math.sin(theta))^2,
(Modelica.Math.sin(theta)*Modelica.Math.cos(theta))};
// Handle float error elements in StiffTrig
for t in 1:size(StiffTrig,1) loop
if abs(StiffTrig[t]) <= float_error then
StiffTrig[t] := 0;
end if;
end for;
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[3], -1*StiffTrig[1], -1*StiffTrig[3];
StiffTrig[3], StiffTrig[2], -1*StiffTrig[3], -1*StiffTrig[2];
-1*StiffTrig[1], -1*StiffTrig[3], StiffTrig[1], StiffTrig[3];
-1*StiffTrig[3], -1*StiffTrig[2], StiffTrig[3], StiffTrig[2]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:4 loop
for n in 1:4 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for; end StiffnessMatrixElement; |
|
Stiffness Matrix Global function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,4,4] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop Kg_mat[i,2*n[i,1],2*n[i,1]]:=Ke_mat[i,2,2]; Kg_mat[i,2*n[i,1]-1,2*n[i,1]-1]:=Ke_mat[i,1,1]; Kg_mat[i,2*n[i,1],2*n[i,1]-1]:=Ke_mat[i,2,1]; Kg_mat[i,2*n[i,1]-1,2*n[i,1]]:=Ke_mat[i,1,2]; Kg_mat[i,2*n[i,2],2*n[i,2]]:=Ke_mat[i,4,4]; Kg_mat[i,2*n[i,2]-1,2*n[i,2]-1]:=Ke_mat[i,3,3]; Kg_mat[i,2*n[i,2],2*n[i,2]-1]:=Ke_mat[i,4,3]; Kg_mat[i,2*n[i,2]-1,2*n[i,2]]:=Ke_mat[i,3,4]; Kg_mat[i,2*n[i,2],2*n[i,1]]:=Ke_mat[i,4,2]; Kg_mat[i,2*n[i,2]-1,2*n[i,1]-1]:=Ke_mat[i,3,1]; Kg_mat[i,2*n[i,2],2*n[i,1]-1]:=Ke_mat[i,4,1]; Kg_mat[i,2*n[i,2]-1,2*n[i,1]]:=Ke_mat[i,3,2]; Kg_mat[i,2*n[i,1],2*n[i,2]]:=Ke_mat[i,2,4]; Kg_mat[i,2*n[i,1]-1,2*n[i,2]-1]:=Ke_mat[i,1,3]; Kg_mat[i,2*n[i,1],2*n[i,2]-1]:=Ke_mat[i,2,3]; Kg_mat[i,2*n[i,1]-1,2*n[i,2]]:=Ke_mat[i,1,4]; end for; end StiffnessMatrixGlobal; |
|
Sum of Stiffness Matrix Global function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal; |
|
Implement Boundary Condition function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:1 loop
KgB_met[2*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:1 loop
KgB_met[2*Boundary_met[a]-b,z*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
|
|
Gauss-Jordan function GaussJordan input Integer x; input Real [x,x] KgB_met; input Real [x] load_met; output Real [x] U_met; Real float_error = 10e-10; algorithm U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan; |
|
Reaction Force function ReactionForce input Integer x; input Real [x,x] KgTot_met; input Real [x] U_met; input Real [x] load_met; output Real [x] R_met; algorithm R_met := (KgTot_met*U_met)-load_met; end ReactionForce; |
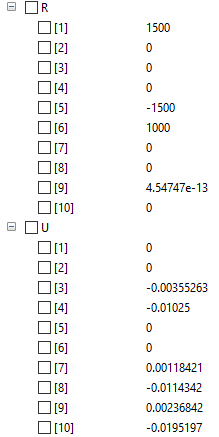
Hasil yang didapat sebagai berikut:
Untuk menyelesaikan soal no.8 saya menggunakan coding berikut:
- Class
|
Fungsi Utama class QuizSoal1
parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5;
2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5;
3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {2,3,4};
parameter Real [:,4] node_load = [1, 0, -5000, 0;
2, 0, 0, 0;
3, 0, 0, 0;
4, 0, 0, 0];
parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(node, x, y, Ke); KgTot = SumStiffnessMatrixGlobal(x, y, Kg); KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); U = GaussJordan(x, KgB, load); R = ReactionForce(x, KgTot, U, load); end QuizSoal1; |
- Function
|
Stiffness Matrix Element function StiffnessMatrixElement input Real [:,9] inisiasi_mat; output Real [size(inisiasi_mat,1),6,6] Ke_mat; protected Real cos_x; Real cos_y; Real cos_z; Real [6] StiffTrig; Real [6,6] StiffTrans; Real [size(inisiasi_mat,1)] k_vec; algorithm
k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member for i in 1:size(inisiasi_mat,1) loop // Clearing the matrices StiffTrig := zeros(6); StiffTrans := zeros(6,6); // Converting degrees to radians cos_x := inisiasi_mat[i,4]; cos_y := inisiasi_mat[i,5]; cos_z := inisiasi_mat[i,6]; // {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for; end StiffnessMatrixElement; |
|
Stiffness Matrix Global function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; end for; end StiffnessMatrixGlobal; |
|
Sum of Stiffness Matrix Global function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal; |
|
Implement Boundary Condition function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
|
|
Gauss-Jordan function GaussJordan input Integer x; input Real [x,x] KgB_met; input Real [x] load_met; output Real [x] U_met; protected Real float_error = 10e-10; algorithm U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan; |
|
Reaction Force function ReactionForce input Integer x; input Real [x,x] KgTot_met; input Real [x] U_met; input Real [x] load_met; output Real [x] R_met; algorithm R_met := (KgTot_met*U_met)-load_met; end ReactionForce; |
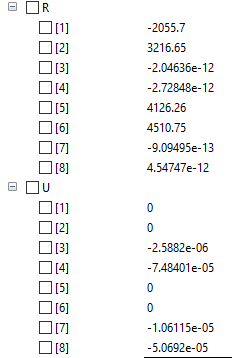
Hasil yang didapat sebagai berikut:
File yang saya guanakan dapat didownload di: https://drive.google.com/drive/folders/1AnQHiRUe-K2XEDtH4xx4_cW30bjYSly-?usp=sharing
PERTEMUAN 5
Pada pertemuan ini kami membahas tentang soal quiz yang telah diberikan pada pertemuan pekan 4. Jadi fungsi mempelajari soal ini adalah agar kita dapat lebih memahami pengaplikasian dari software openmodelica pada contoh kasus yang real. Pertemuan ini menjelaskan bagaimana alur pengerjaan soal quiz yang diberikan agar dapat membuat semua persamaan yang dapat digunakan pada kasus yang lebih universal.
Pada pertemuan ini juga saya diminta Pak Dai untuk menjelaskan kepada teman-teman di kelas tentang fungsi-fungsi yang saya gunakan untuk mengerjakan soal quiz 1. Beberapa hal yang saya jelaskan antara lain:
- Cara melakukan looping menggunakan fungsi for.
- Cara membuat data dalam bentuk array.
- Cara menggunakan fungsi if.
- Apa itu floating number dan bagaimana cara menghilangkannya.
- Apa itu protected variable.
- Fungsi dari modelica class dengan specialization class dan function.
TUGAS 4
PROGRES REVISI
- Pada revisi pertama saya menambahkan (pada perhitungan pada struktur 2D dan 3D) sebuah class function untuk melakukan pengecekan gaya total (gaya reaksi + gaya load) apakah sudah bernilai 0 pada tiap sumbu atau belum, serta menyederhanakan proses input dengan membuang beberapa variable dan nilai-nilai pada variable tertentu yang tidak diperlukan.
- Pada revisi kedua ini saya menambahkan (pada perhitungan pada struktur 2D dan 3D) variable baru untuk menghitung pada kondisi boundary yang berbeda sehingga perhitungan bisa dilakukan pada kondisi tumpuan yang berbeda-beda.
- Pada revisi ketiga ini saya mengubah (pada perhitungan pada struktur 3D, untuk 2D masih belum selesai) input data awal yang dibutuhkan. Pada versi sebelumnya saya perlu menghitung panjang batang dan untuk struktur 3D perlu menghitung nilai cos(theta)x, cos(theta)y, dan cos(theta)z secara manual terlebih dahulu. Pada versi ini, saya hanya perlu memasukkan nilai selisih node j dan node i tiap batang pada tiap sumbu saja sehingga perhitungan yang sebelumnya dilakukan secara manual sekarang bisa dilakukan secara otomatis.
Untuk melihat file progres yang telah saya buat dapat dicek pada link berikut: https://drive.google.com/drive/folders/1SJrgAd46puniIpk4ULvx3Dpr1wcFlUD6?usp=sharing
PENGERJAAN SOAL
Berikut adalah coding input yang saya gunakan pada file revisi ketiga:
|
Fungsi Utama class QuizSoal1
//inisiasi = [ elemen#, dX, dY, dZ, A, E]
parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data
2, 0, 0, -6, 1.56, 10.6e6;
3, 0, 6, -3, 1.56, 10.6e6;
4, -6, 0, -3, 1.56, 10.6e6;
5, -6, 6, 0, 1.56, 10.6e6;
6, 0, 6, 3, 1.56, 10.6e6];
//node = [ i, j]
parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
//jumlah node parameter Integer n = 4; //isi sesuai data //titik node boundary xyz
parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data
//titik node boundary xy
parameter Integer [:] Boundary_xy = {4}; //isi sesuai data
//titik node boundary xz
parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
//titik node boundary yz
parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
//titik node boundary x
parameter Integer [:] Boundary_x = {3}; //isi sesuai data
//titik node boundary y
parameter Integer [:] Boundary_y = {0}; //isi sesuai data
//titik node boundary z
parameter Integer [:] Boundary_z = {0}; //isi sesuai data
//load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
parameter Real [3*n] load = {0, 0, 0, //isi sesuai data
0, -200, 0,
0, 0, 0,
0, 0, 0};
Real [size(inisiasi,1)] L; Real [size(inisiasi,1)] k; Real [size(inisiasi,1),6,6] Ke; Real [size(inisiasi,1),3*n,3*n] Kg; Real [3*n,3*n] KgTot; Real [3*n,3*n] KgB; Real [3*n] U; Real [3*n] R; //check force Real [3] F; equation
L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(n, node, Ke); KgTot = SumStiffnessMatrixGlobal(Kg); KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); U = GaussJordan(KgB, load); R = ReactionForce(KgTot, U, load); F = CheckForce(load,R); end QuizSoal1; |
Hasil yang saya dapat dari menggunakan perhitungan pada file revisi ketiga saya adalah sebagai berikut:
APLIKASI METODE NUMERIK DALAM KASUS OPTIMISASI
Function to be solved
function Func_Optimization input Real x; import Modelica.Math; output Real y; algorithm y:=2*sin(x)-x^2/10; end Func_Optimization;
Optimization - Golden Section
model Opt_Gold
parameter Real xlo=0;
parameter Real xhi=4;
parameter Integer N=8; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=Func_Optimization(x1[i]);
f2[i]:=Func_Optimization(x2[i]);
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Optimization - Newton
model Opt_Newton parameter Real g=2.5; //initial guess parameter Integer N=8; // maximum iteration parameter Real es=0.0001; // maximum error Real X[N]; Real xopt, fx, ea[N]; algorithm X[1]:=g; ea[1]:=1; for i in 2:N loop X[i]:=X[i-1]-Func_Optimization_Der(X[i-1])/Func_Optimization_Der_Der(X[i-1]); xopt:=X[i]; ea[i]:=abs(1-X[i-1]/X[i]); if ea[i]<es then break; end if; end for; fx:=Func_Optimization(xopt); end Opt_Newton;
Optimization - Parabolic
model Opt_Parabolic
parameter Real g1=0; //initial guess
parameter Real g2=1; //initial guess
parameter Real g3=4; //initial guess
parameter Integer N=5; // maximum iteration
parameter Real es=0.0001; // maximum error
Real x1, x2, x3, xopt, xp[N], ea[N];
//Real xl, xm, xu;
Real fx1, fx2, fx3, fx, A[4], A_star[4];
algorithm
x1:=g1;
x2:=g2;
x3:=g3;
for i in 1:N loop
fx1:=Func_Optimization(x1);
fx2:=Func_Optimization(x2);
fx3:=Func_Optimization(x3);
xp[i]:=(fx1*(x2^2-x3^2)+fx2*(x3^2-x1^2)+fx3*(x1^2-x2^2))/(2*fx1*(x2-x3)+2*fx2*(x3-x1)+2*fx3*(x1-x2));
xopt:=xp[i];
fx:=Func_Optimization(xp[i]);
A:={x1,x2,x3,xp[i]};
A_star:=Modelica.Math.Vectors.sort(A);
if xp[i]>x2 then
x1:=A_star[2];
x2:=A_star[3];
x3:=A_star[4];
else
x1:=A_star[1];
x2:=A_star[2];
x3:=A_star[3];
end if;
end for;
ea[1]:=1;
for i in 2:N loop
ea[i]:=abs(1-xp[i-1]/xp[i]);
if ea[i]<es then
break;
end if;
end for;
end Opt_Parabolic;
TUGAS BESAR
Pendahuluan
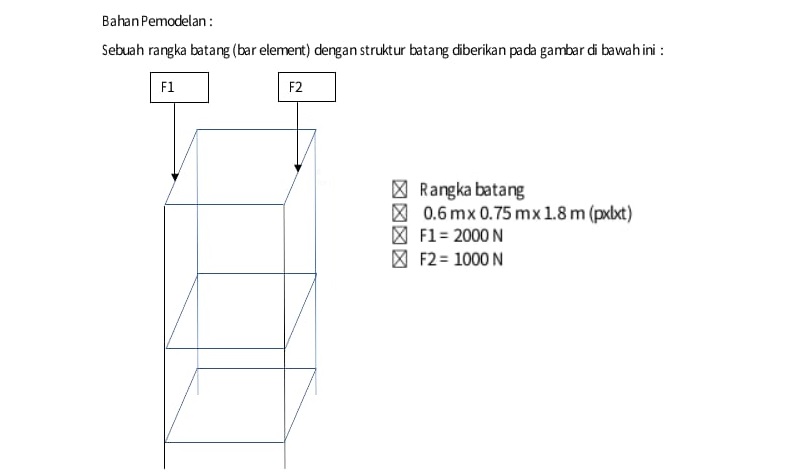
Pada tugas besar ini, kami diberikan sebuah tugas untuk melakukan optimisasi pemilihan material dan luas penampang trusses yang akan digunakan untuk membuat konstruksi sebagai berikut:
Asumsi yang digunakan untuk melakukan perhitungan ini antara lain:
- Beban akan terdistribusi hanya pada node (karena bersifat trusses).
- Safety factor minimal bernilai 2.
- Batas displacement 0,001 m sebelum buckling (pada truss paling atas).
- Ketinggian trusses pada tiap lantai sama yaitu 0,6 m.
Metodologi
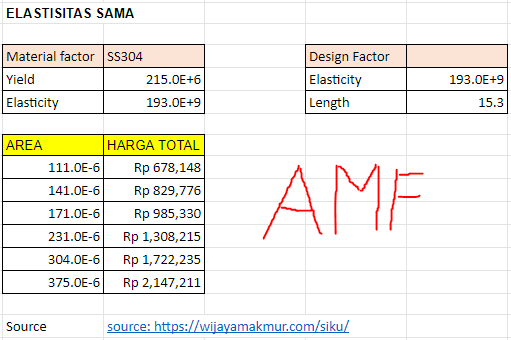
Untuk jenis material yang sama:
- Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu SS304.
- Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting.
- Melakukan optimasi menggunakan metode golden section.
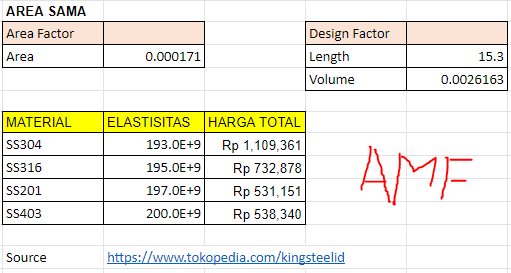
Untuk area penampang yang sama:
- Mencari harga untuk 4 jenis material dengan area penampang yang sama yaitu 171 mm^2.
- Mengitung nilai safety factor pada 4 jenis batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting.
- Melakukan optimasi menggunakan metode golden section.
Data yang Digunakan
Coding yang Digunakan
- Untuk perhitungan displacement, reaction force, stress, dan safety factor:
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
- Untuk membuat kurva curve fitting:
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
- Untuk golden section:
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
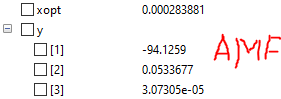
Hasil Perhitungan
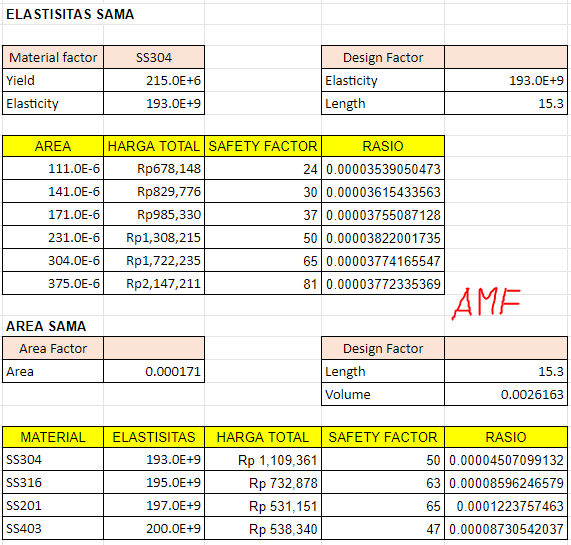
- Nilai rasio dari safety factor dengan harga
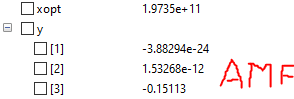
- Nilai luas area penampang optimum untuk material SS304 adalah 284mm^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 30mm dan tebal 4mm.
- Material optimum yang dapat digunakan untuk luas penampang 171mm^2 adalah material dengan nilai elastisitas 19735000000000 N/m^2 atau material yang paling mendekati adalah SS201.