Irfan Rahadi Kurninato
السلام عليكم Irfan Rahadi Kurnianto - 1706036255
Contents
[hide]
4 September 2019
Mengapa kita harus belajar kalkulus? kalkulus adalah mata kuliah dasar teknik. Mata kuliah kalkulus sangat berguna untuk membentuk logika agar mudah dalam belajar suatu hal lain
Tugas 1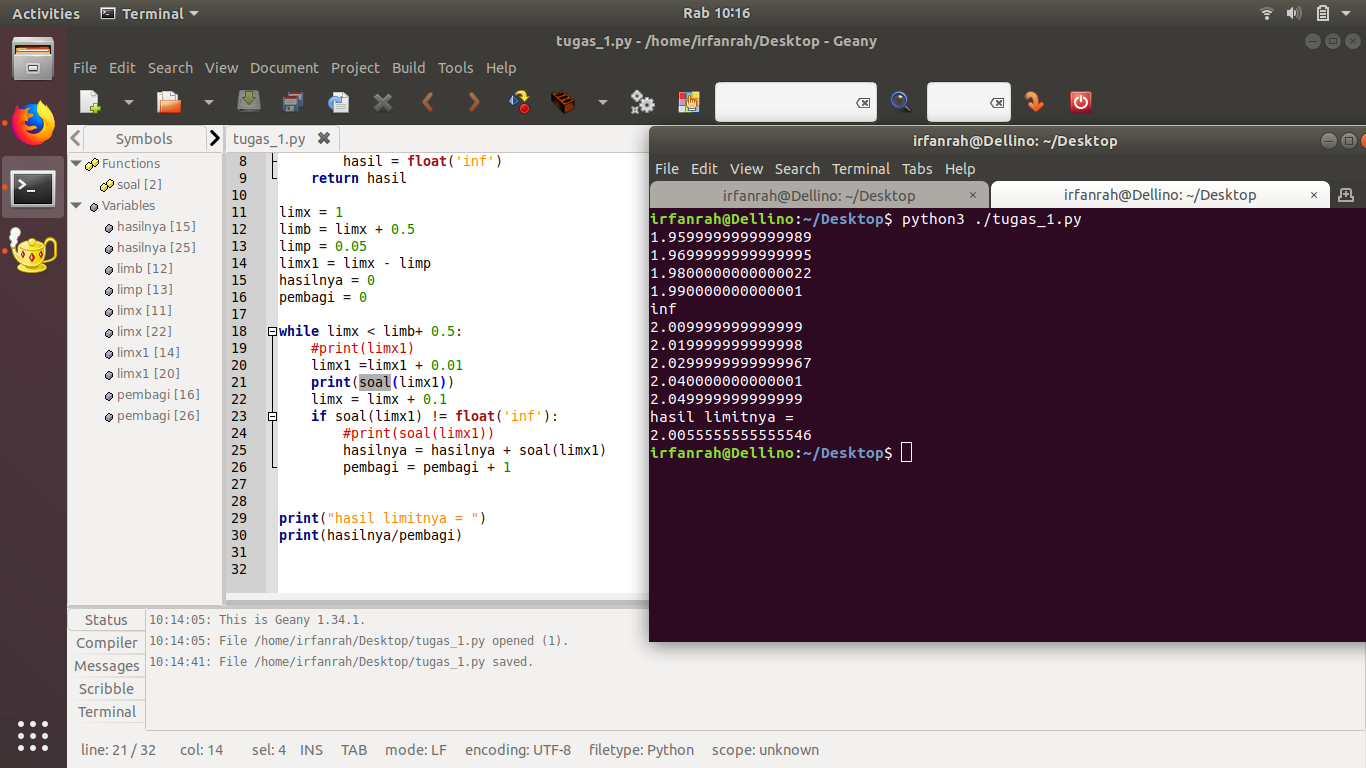
11 September 2019
Bit Komputer Program Catur
coding bukan pelajaran anak fasilkom/elektro belajar python praktek programing dasar2 programing + pyhton programnya irfan t2 dikelas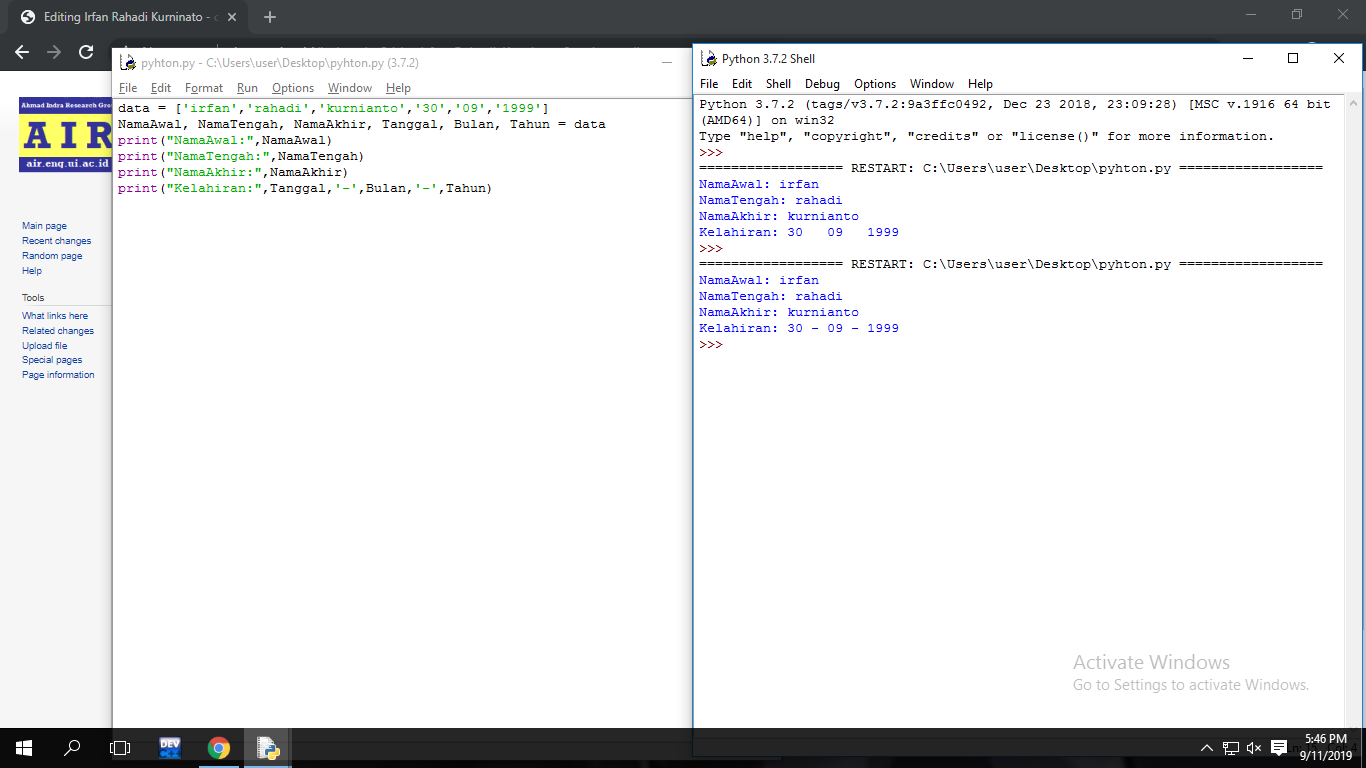
18 September 2019
Tugas irfan 18 sep 19
25 September 2019
Tugas irfan 25 sep 19 catatan irfan 25 sep 19
2 Oktober 2019
Metode numerik adalah teknik-teknik yang digunakan untuk merumuskan masalah-masalah matematika agar dapat diselesaikan dengan operasi-operasi aritmatika (hitungan) biasa (tambah, kurang, kali, dan bagi). Secara harfiah metode numerik berarti cara berhitung dengan menggunakan angka-angka.
9 Oktober 2019
Metode Runge-Kutta Persamaan Diferensial Biasa (PDB) adalah persamaan yang melibatkan satu atau lebih turunan fungsi satu peubah. Solusi dari PDB adalah fungsi tertentu yang memenuhi persamaan tersebut.
kuis 16 Oktober 2019
program runge kutta
https://pastebin.com/GxfenTa3 # dibuat oleh irfan rahadi 1706036255 def TurunanY(x, y): #Fungsi Turunan Y return ((x**2 - 4*y)) xawal = 0 #boundary condition x awal soal yinit = 1 #boundary condition y awal soal x = 0.03 #nilai x yang ditanya h = 0.01 #delta yang digunakan angka = (int)((x - xawal)/h) #menghitung jumlah increment yg diperlukan for i in range(1, angka + 1): k1 = h * TurunanY(xawal, yinit) #rumus runge kutta k2 = h * TurunanY(xawal + 0.5 * h, yinit + 0.5 * k1) k3 = h * TurunanY(xawal + 0.5 * h, yinit + 0.5 * k2) k4 = h * TurunanY(xawal + h, yinit + k3) yinit = yinit + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #menjumlahkan nilai k1,k2,k3,k4 ke y' yang baru dan membaginya xawal = xawal + h #menambahkan xawal besarkan delta h print(yinit)
PROGRAM GAUSS
from numpy import linalg
import numpy as np
a= np.array ([[0,0,2,1,2] ,[0,1,0,2,-1], [1,2,0,-2,1], [0,0,0,-1,1], [0,1,-1,1,-1]])
b= np.array ([[1], [1], [-4], [-2], [-1]])
c= np.array ([[0,0,2,1,2,1] ,[0,1,0,2,-1,1], [1,2,0,-2,1,-4], [0,0,0,-1,1,-2], [0,1,-1,1,-1,-1]])
print ("Matrix a " , a)
print ("Matrix b ", b)
print ("Matrixnya adalah:" , c)
matsolve = linalg.solve (a,c)
x1 = int(matsolve[0])
x2 = int(matsolve[1])
x3 = int(matsolve[2])
x4 = int(matsolve[3])
x5 = int(matsolve[4])
hasil= (x1, x2, x3, x4, x5)
print ("Hasil nilai x1,x2,x3,x4,x5 :")
print (hasil)
UTS 23 oktober
Video Muhasabah
3 A
# Cara 1
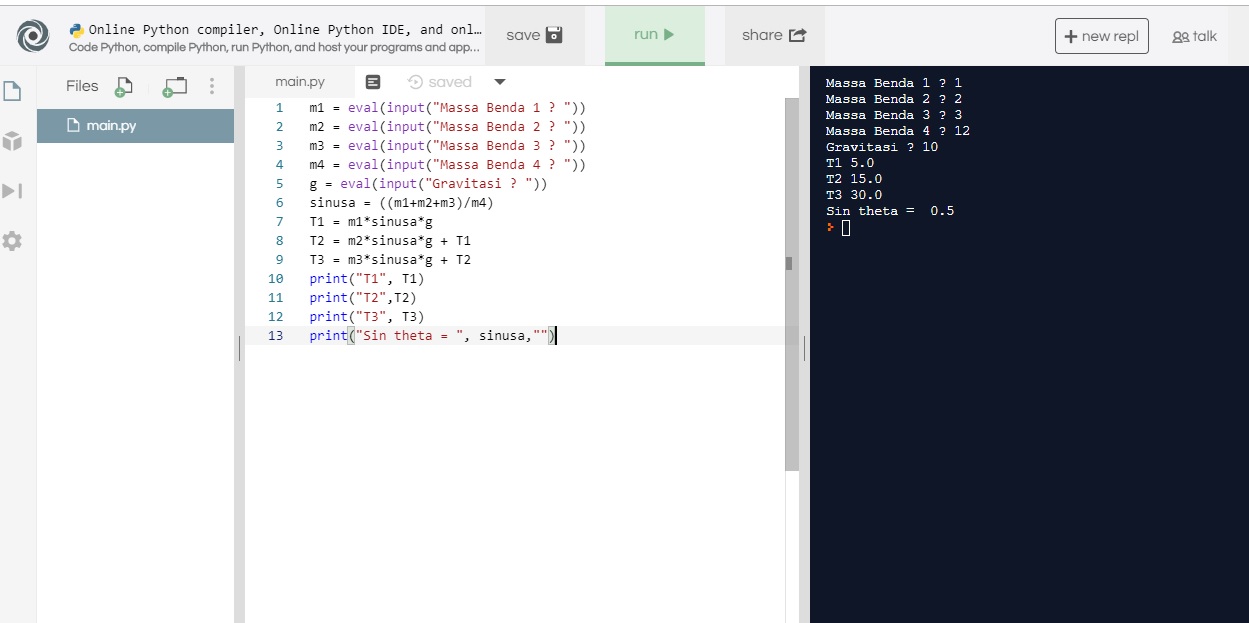
m1 = eval(input("Massa Benda 1 ? ")) #menginput m1
m2 = eval(input("Massa Benda 2 ? "))#menginput m2
m3 = eval(input("Massa Benda 3 ? ")) #meninput m3
m4 = eval(input("Massa Benda 4 ? "))
g = eval(input("Gravitasi ? ")) #input g
sinusa = ((m1+m2+m3)/m4)#hitung sin theta
T1 = m1*sinusa*g #hitung T1
T2 = m2*sinusa*g + T1 #hitung T2
T3 = m3*sinusa*g + T2 #hitung T3
print("T1", T1)
print("T2",T2)
print("T3", T3)
print("Sin theta = ", sinusa,"")
 #Cara 2
m1 = eval(input("Massa Benda 1 ? "))
m2 = eval(input("Massa Benda 2 ? "))
m3 = eval(input("Massa Benda 3 ? "))
m4 = eval(input("Massa Benda 4 ? "))
g = eval(input("Gravitasi ? "))
sinusa = ((m1+m2+m3)/m4)
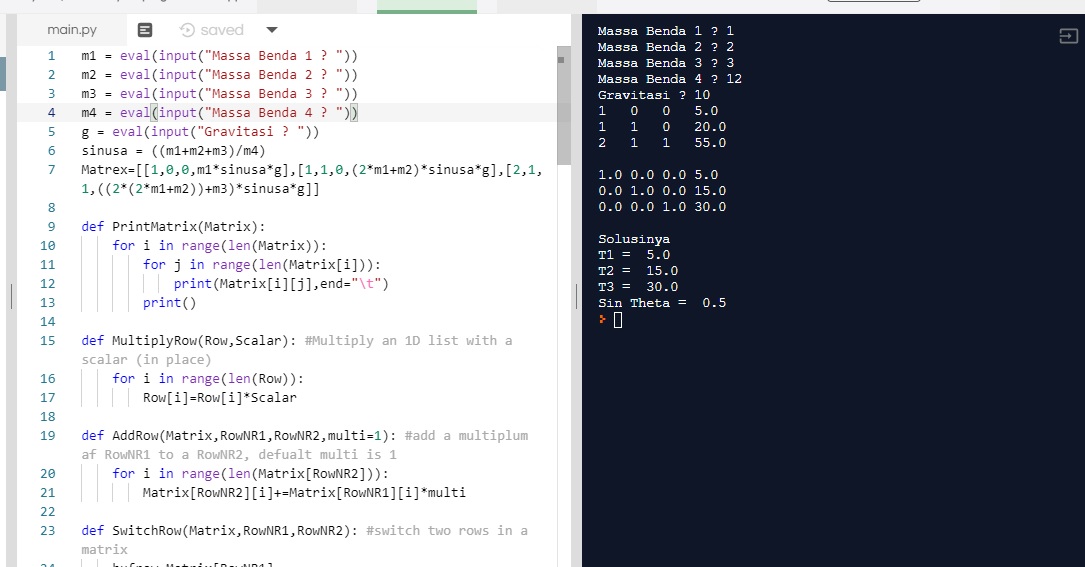
Matrex=[[1,0,0,m1*sinusa*g],[1,1,0,(2*m1+m2)*sinusa*g],[2,1,1,((2*(2*m1+m2))+m3)*sinusa*g]] #Matrix yg mau di gauss
def PrintMatrix(Matrix): #untuk print
for i in range(len(Matrix)):
for j in range(len(Matrix[i])):
print(Matrix[i][j],end="\t")
print()
def MultiplyRow(Row,Scalar): #untuk kali
for i in range(len(Row)):
Row[i]=Row[i]*Scalar
def AddRow(Matrix,RowNR1,RowNR2,multi=1): #untuk tambah
for i in range(len(Matrix[RowNR2])):
Matrix[RowNR2][i]+=Matrix[RowNR1][i]*multi
def SwitchRow(Matrix,RowNR1,RowNR2): #untuk tukar
bufrow=Matrix[RowNR1]
Matrix[RowNR1]=Matrix[RowNR2]
Matrix[RowNR2]=bufrow
return 0
def ZeroRowsBelow(Matrix,RowNR,CollumnNR): #untuk menghindari eror 0
for i in range(len(Matrix)-RowNR-1):
if not(Matrix[RowNR][CollumnNR]==0):
AddRow(Matrix,RowNR,i+1+RowNR,-float(Matrix[i+1+RowNR][CollumnNR])/Matrix[RowNR][CollumnNR])
#print(i)
def SolveMatrix(Matrix): #untuk mensolve
#Bring To Row-Echelon Form
for i in range(len(Matrex)):
ZeroRowsBelow(Matrex,i,i)
#Make Row-Echelon 1
for i in range(len(Matrex)):
if not(Matrex[i][i]==0):
MultiplyRow(Matrex[i],1./Matrex[i][i])
#diulang lagi
for i in range(len(Matrex)):
for j in range(i):
if not(Matrex[i][i]==0):
AddRow(Matrex,i,j,-float(Matrex[j][i])/Matrex[i][i])
def IsRRowEchelon(Matrix): #cek selsai
for i in range(len(Matrix)):
pos=[1,0]
if not(Matrix[i][i] in pos):
return 0
return 1
def CheckForEqualRows(Matrix):#cek nilai
newlist=[]
for i in Matrix:
if i not in newlist:
newlist.append(i)
return newlist
MatrixNew=[]
for j in range(len(Matrex)):
RowNew=[]
for i in range(len(Matrex[j])):
RowNew.append(Matrex[j][i])
MatrixNew.append(RowNew)
Matrex=MatrixNew
PrintMatrix(Matrex)
print()
while True:
SolveMatrix(Matrex)
Matrex=CheckForEqualRows(Matrex)
if IsRRowEchelon(Matrex):
break
PrintMatrix(Matrex)#print matrix
print("")
print("Solusinya")
print("T1 = ",Matrex[0][3])
print("T2 = ",Matrex[1][3])
print("T3 = ",Matrex[2][3])
print("Sin Theta = ",Matrex[0][3]/(m1*g))
#Cara 2
m1 = eval(input("Massa Benda 1 ? "))
m2 = eval(input("Massa Benda 2 ? "))
m3 = eval(input("Massa Benda 3 ? "))
m4 = eval(input("Massa Benda 4 ? "))
g = eval(input("Gravitasi ? "))
sinusa = ((m1+m2+m3)/m4)
Matrex=[[1,0,0,m1*sinusa*g],[1,1,0,(2*m1+m2)*sinusa*g],[2,1,1,((2*(2*m1+m2))+m3)*sinusa*g]] #Matrix yg mau di gauss
def PrintMatrix(Matrix): #untuk print
for i in range(len(Matrix)):
for j in range(len(Matrix[i])):
print(Matrix[i][j],end="\t")
print()
def MultiplyRow(Row,Scalar): #untuk kali
for i in range(len(Row)):
Row[i]=Row[i]*Scalar
def AddRow(Matrix,RowNR1,RowNR2,multi=1): #untuk tambah
for i in range(len(Matrix[RowNR2])):
Matrix[RowNR2][i]+=Matrix[RowNR1][i]*multi
def SwitchRow(Matrix,RowNR1,RowNR2): #untuk tukar
bufrow=Matrix[RowNR1]
Matrix[RowNR1]=Matrix[RowNR2]
Matrix[RowNR2]=bufrow
return 0
def ZeroRowsBelow(Matrix,RowNR,CollumnNR): #untuk menghindari eror 0
for i in range(len(Matrix)-RowNR-1):
if not(Matrix[RowNR][CollumnNR]==0):
AddRow(Matrix,RowNR,i+1+RowNR,-float(Matrix[i+1+RowNR][CollumnNR])/Matrix[RowNR][CollumnNR])
#print(i)
def SolveMatrix(Matrix): #untuk mensolve
#Bring To Row-Echelon Form
for i in range(len(Matrex)):
ZeroRowsBelow(Matrex,i,i)
#Make Row-Echelon 1
for i in range(len(Matrex)):
if not(Matrex[i][i]==0):
MultiplyRow(Matrex[i],1./Matrex[i][i])
#diulang lagi
for i in range(len(Matrex)):
for j in range(i):
if not(Matrex[i][i]==0):
AddRow(Matrex,i,j,-float(Matrex[j][i])/Matrex[i][i])
def IsRRowEchelon(Matrix): #cek selsai
for i in range(len(Matrix)):
pos=[1,0]
if not(Matrix[i][i] in pos):
return 0
return 1
def CheckForEqualRows(Matrix):#cek nilai
newlist=[]
for i in Matrix:
if i not in newlist:
newlist.append(i)
return newlist
MatrixNew=[]
for j in range(len(Matrex)):
RowNew=[]
for i in range(len(Matrex[j])):
RowNew.append(Matrex[j][i])
MatrixNew.append(RowNew)
Matrex=MatrixNew
PrintMatrix(Matrex)
print()
while True:
SolveMatrix(Matrex)
Matrex=CheckForEqualRows(Matrex)
if IsRRowEchelon(Matrex):
break
PrintMatrix(Matrex)#print matrix
print("")
print("Solusinya")
print("T1 = ",Matrex[0][3])
print("T2 = ",Matrex[1][3])
print("T3 = ",Matrex[2][3])
print("Sin Theta = ",Matrex[0][3]/(m1*g))
3 B
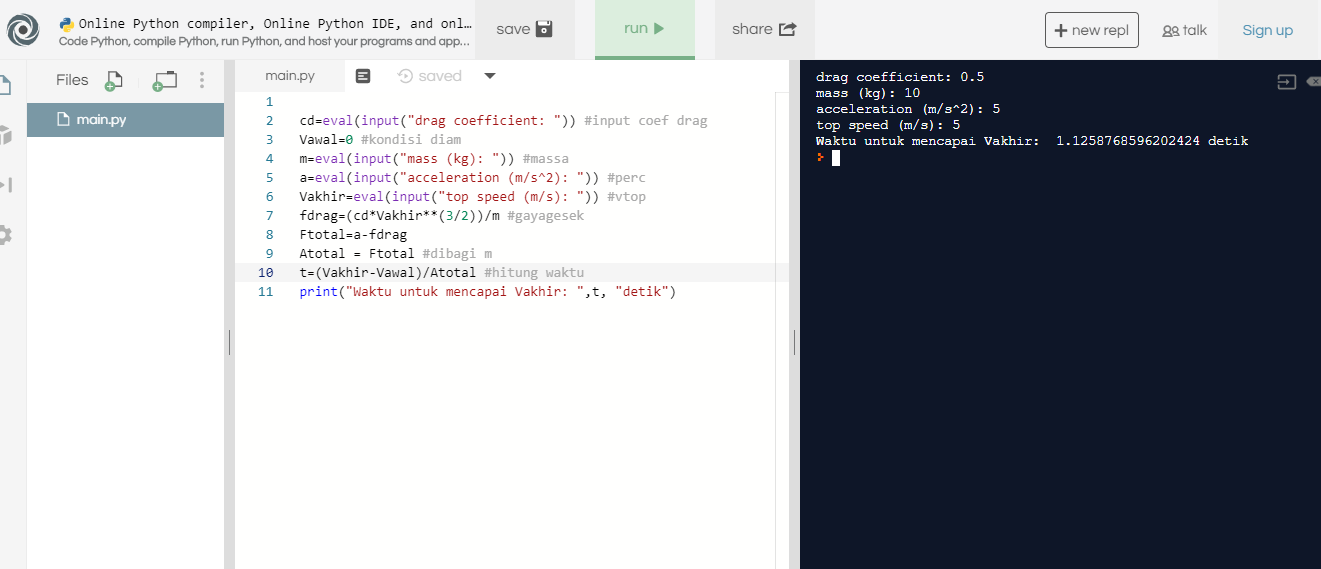
cara 1
cd=eval(input("drag coefficient: ")) #input coef drag
Vawal=0 #kondisi diam
m=eval(input("mass (kg): ")) #massa
a=eval(input("acceleration (m/s^2): ")) #perc
Vakhir=eval(input("top speed (m/s): ")) #vtop
fdrag=(cd*Vakhir**(3/2))/m #gayagesek
Ftotal=a-fdrag
Atotal = Ftotal #dibagi m
t=(Vakhir-Vawal)/Atotal #hitung waktu
print("Waktu untuk mencapai Vakhir: ",t, "detik")
Cara 2
def TurunanKec(perc, vakir): #Fungsi
return (percepatan - ((cd*vakir**(3/2))/m))
cd=eval(input("drag coefficient: ")) #input coef drag
Vawal=0
#kondisi diam
m=eval(input("mass (kg): ")) #massa
percepatan=eval(input("acceleration (m/s^2): "))
#perc
Vakhir=eval(input("top speed (m/s): "))
#vtop
xawal = 0 #boundary condition x awal soal
yinit = 0 #boundary condition y awal soal
x = Vakhir #nilai x yang ditanya
h = 1 #delta yang digunakan
angka = (int)((x - xawal)/h) #menghitung jumlah increment yg diperlukan
for i in range(1, angka + 1):
k1 = h * TurunanKec(xawal, yinit) #rumus runge kutta
k2 = h * TurunanKec(xawal + 0.5 * h, yinit + 0.5 * k1)
k3 = h * TurunanKec(xawal + 0.5 * h, yinit + 0.5 * k2)
k4 = h * TurunanKec(xawal + h, yinit + k3)
yinit = yinit + (1 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #menjumlahkan nilai k1,k2,k3,k4 ke y' yang baru dan membaginya
xawal = xawal + h
#menambahkan xawal besarkan delta h
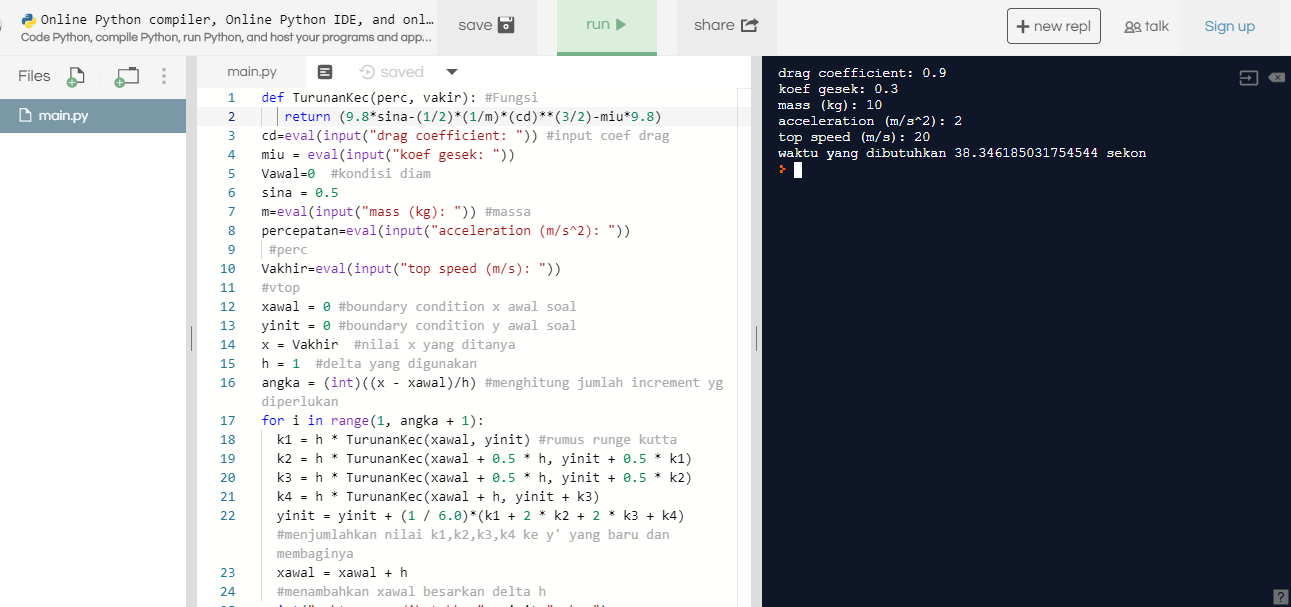
print("waktu yang dibutuhkan", yinit,"sekon")
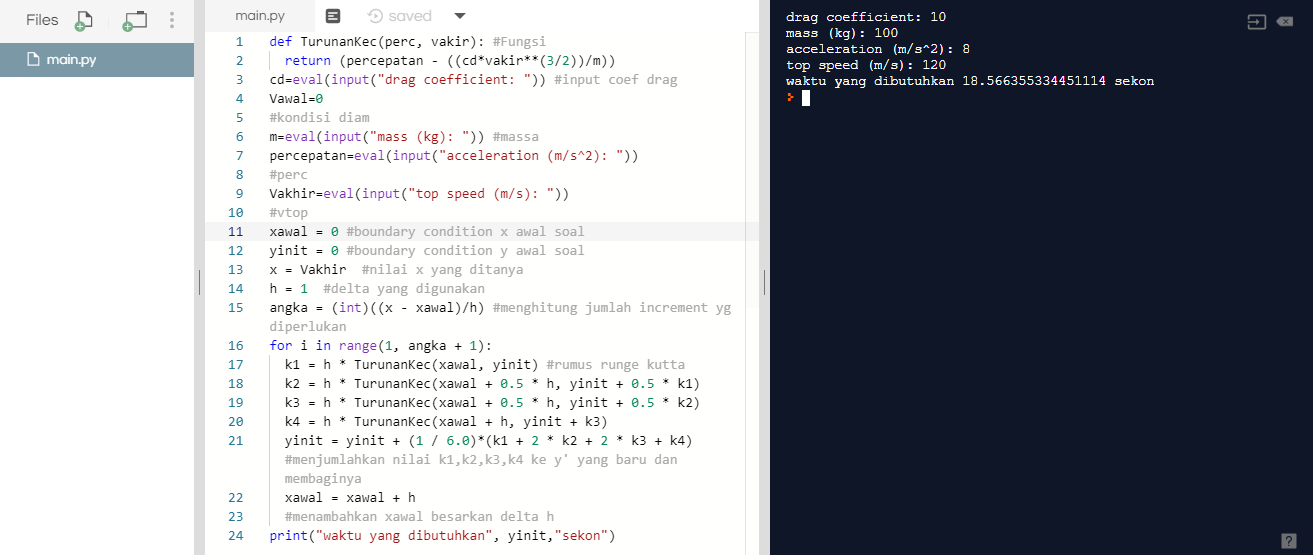
Tugas 30 Oktober
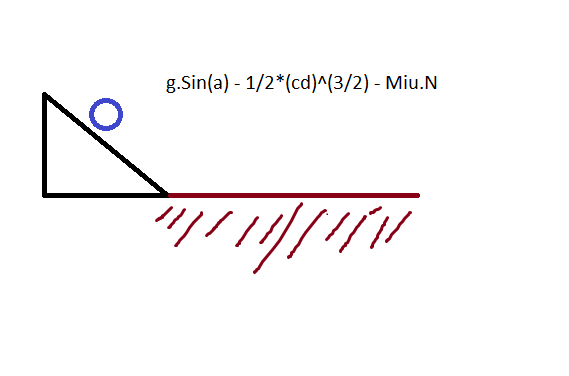
def TurunanKec(perc, vakir): #Fungsi
return (9.8*sina-(1/2)*(1/m)*(cd)**(3/2)-miu*9.8)
cd=eval(input("drag coefficient: ")) #input coef drag
miu = eval(input("koef gesek: "))
Vawal=0 #kondisi diam
sina = 0.5
m=eval(input("mass (kg): ")) #massa
percepatan=eval(input("acceleration (m/s^2): "))
#perc
Vakhir=eval(input("top speed (m/s): "))
#vtop
xawal = 0 #boundary condition x awal soal
yinit = 0 #boundary condition y awal soal
x = Vakhir #nilai x yang ditanya
h = 1 #delta yang digunakan
angka = (int)((x - xawal)/h) #menghitung jumlah increment yg diperlukan
for i in range(1, angka + 1):
k1 = h * TurunanKec(xawal, yinit) #rumus runge kutta
k2 = h * TurunanKec(xawal + 0.5 * h, yinit + 0.5 * k1)
k3 = h * TurunanKec(xawal + 0.5 * h, yinit + 0.5 * k2)
k4 = h * TurunanKec(xawal + h, yinit + k3)
yinit = yinit + (1 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #menjumlahkan nilai k1,k2,k3,k4 ke y' yang baru dan membaginya
xawal = xawal + h
#menambahkan xawal besarkan delta h
print("waktu yang dibutuhkan", yinit,"sekon")
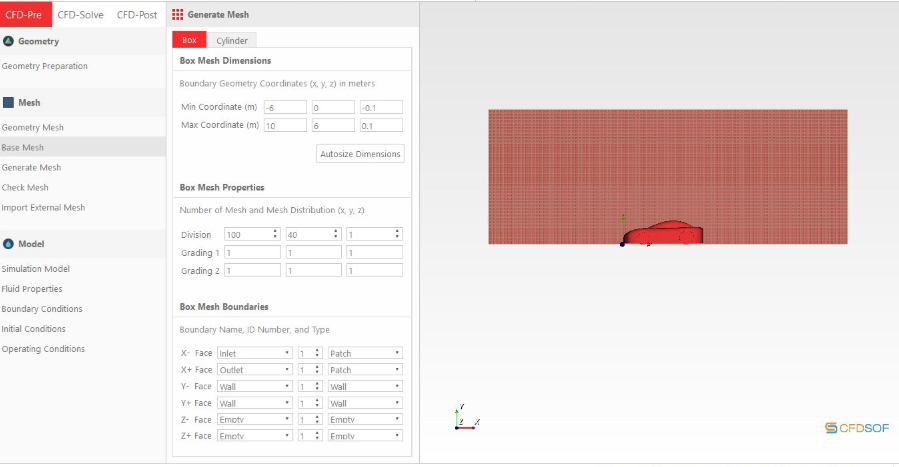
Computational Fluid Dyinamics
Tugas CFD Drag Force
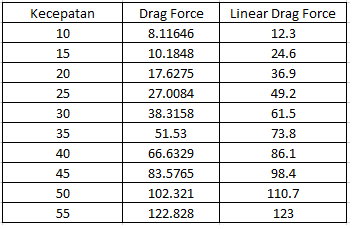
Setelah kami melakukan percobaan dengan 10 variabel kecepatan berbeda menggunakan aplikasi CFDSOF-NG, didapat data sebagai berikut yang nantinya akan di-plotting dan dilakukan curve fitting :
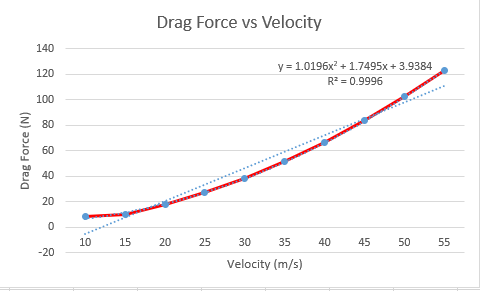
Hasil curve fitting yang kami lakukan di excel seperti pada grafik berikut
Berdasarkan pengolahan tersebut, dapat disimpulkan bahwa hubungan drag force dengan kecepatan pada permasalahan ini sesuai dengan persamaan berikut:
y = 1.0196x2 + 1.7495x + 3.9384
y = Drag Force
x = Velocity
R² = 0.9996
Menunjukan keakuratan dari regresi yang telah dilakukan. Semakin besar nilainya (mendekati 1) maka semakin akurat
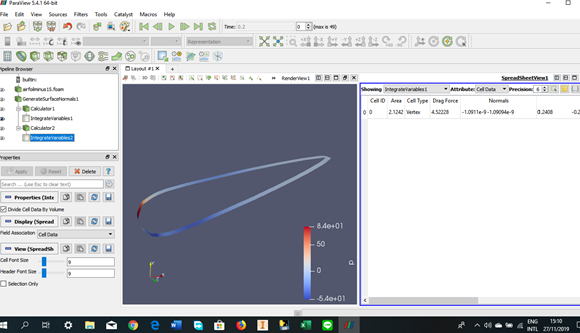
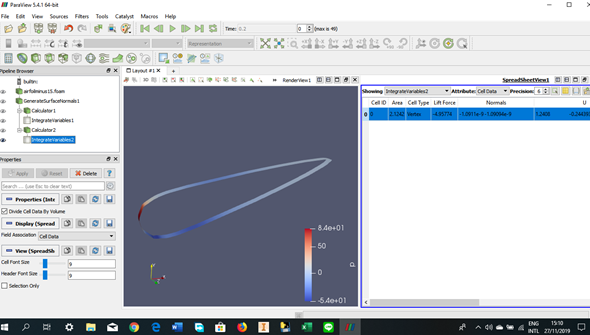
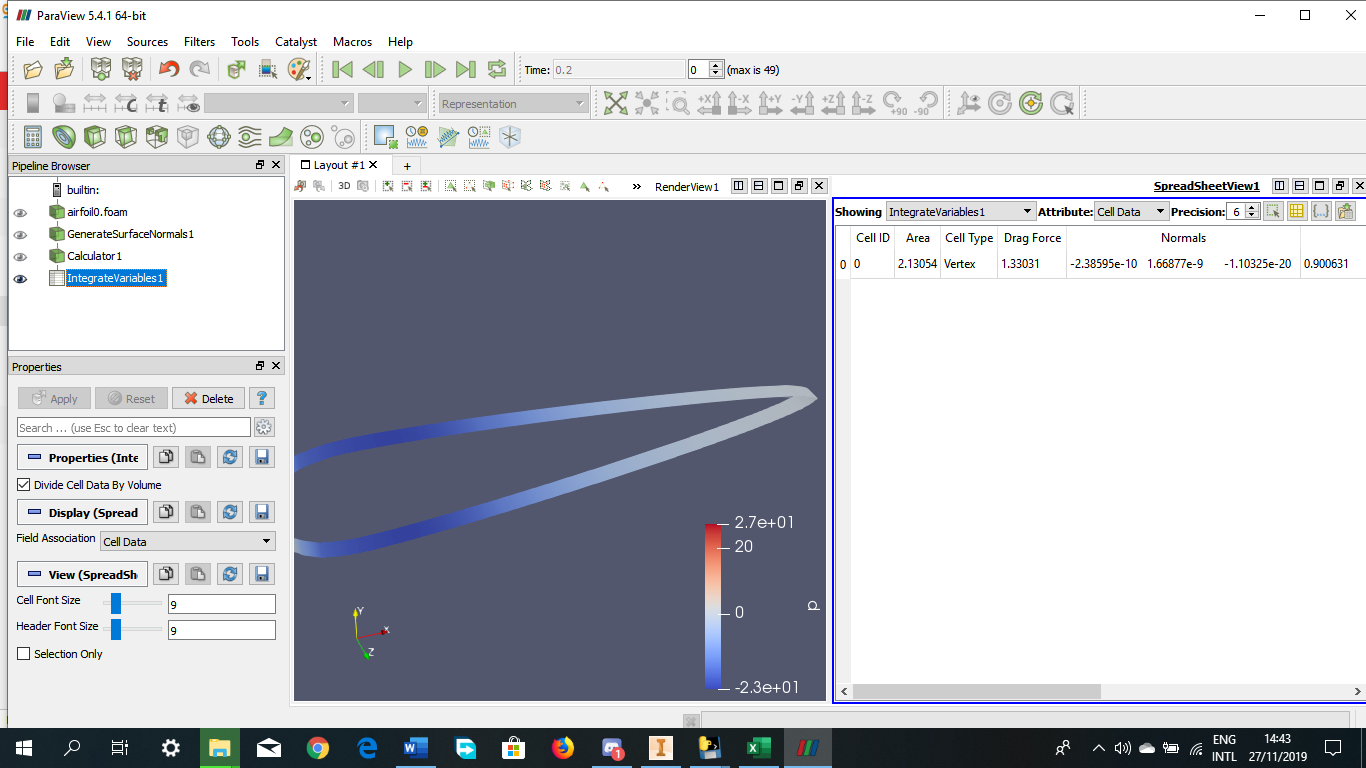
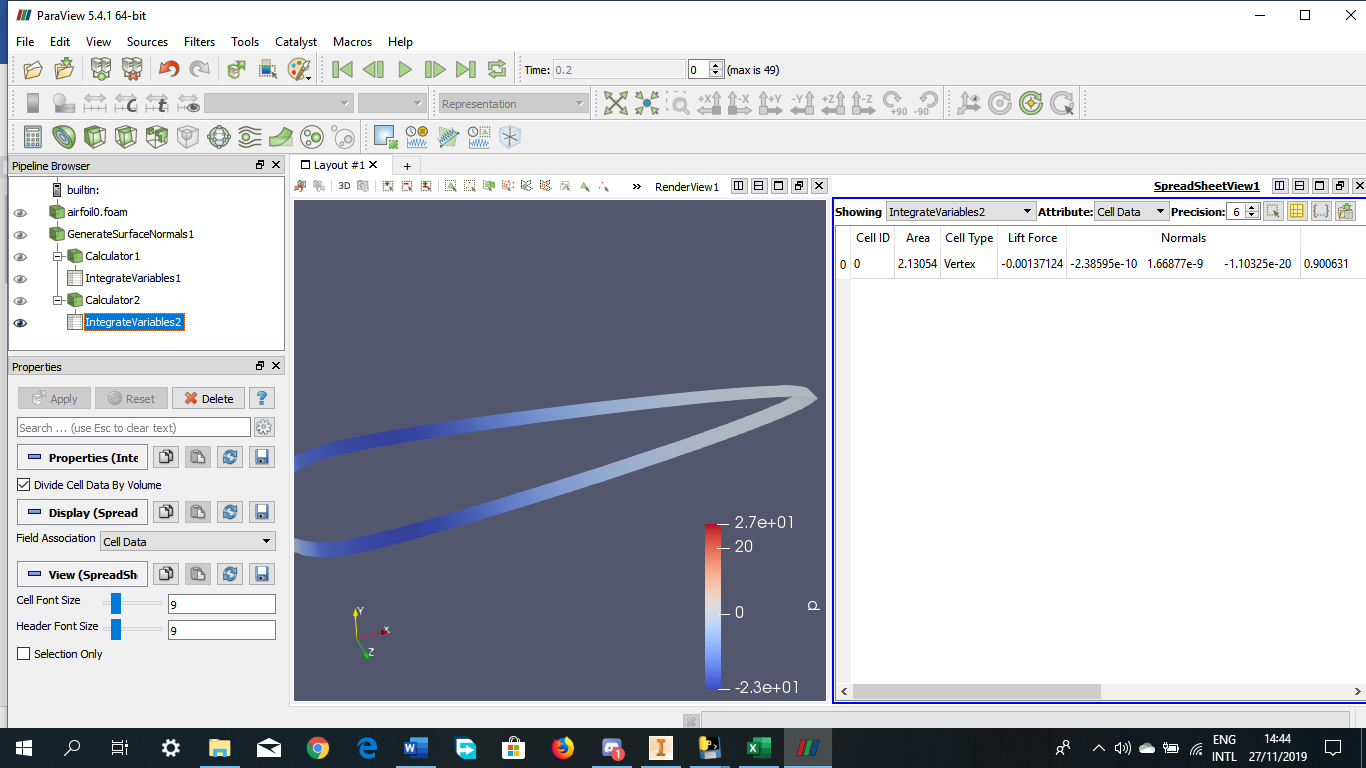
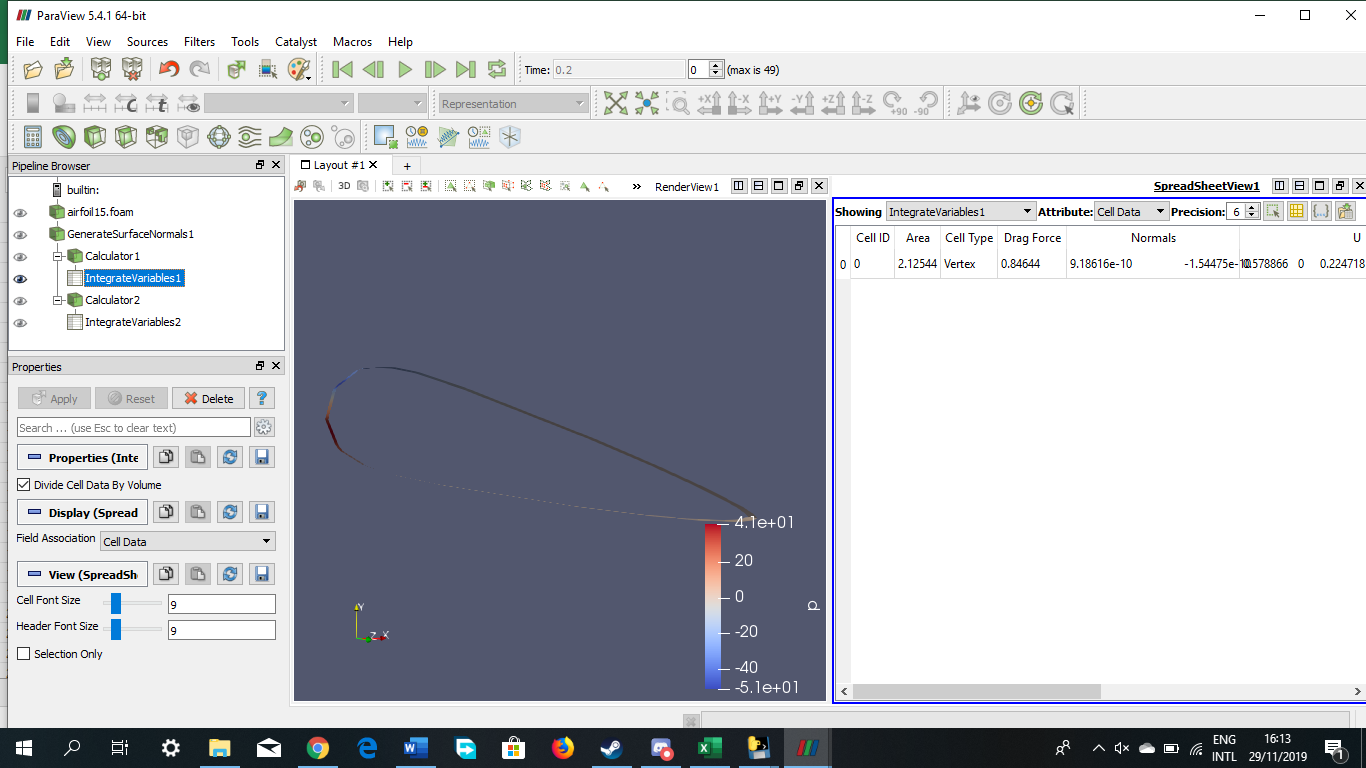
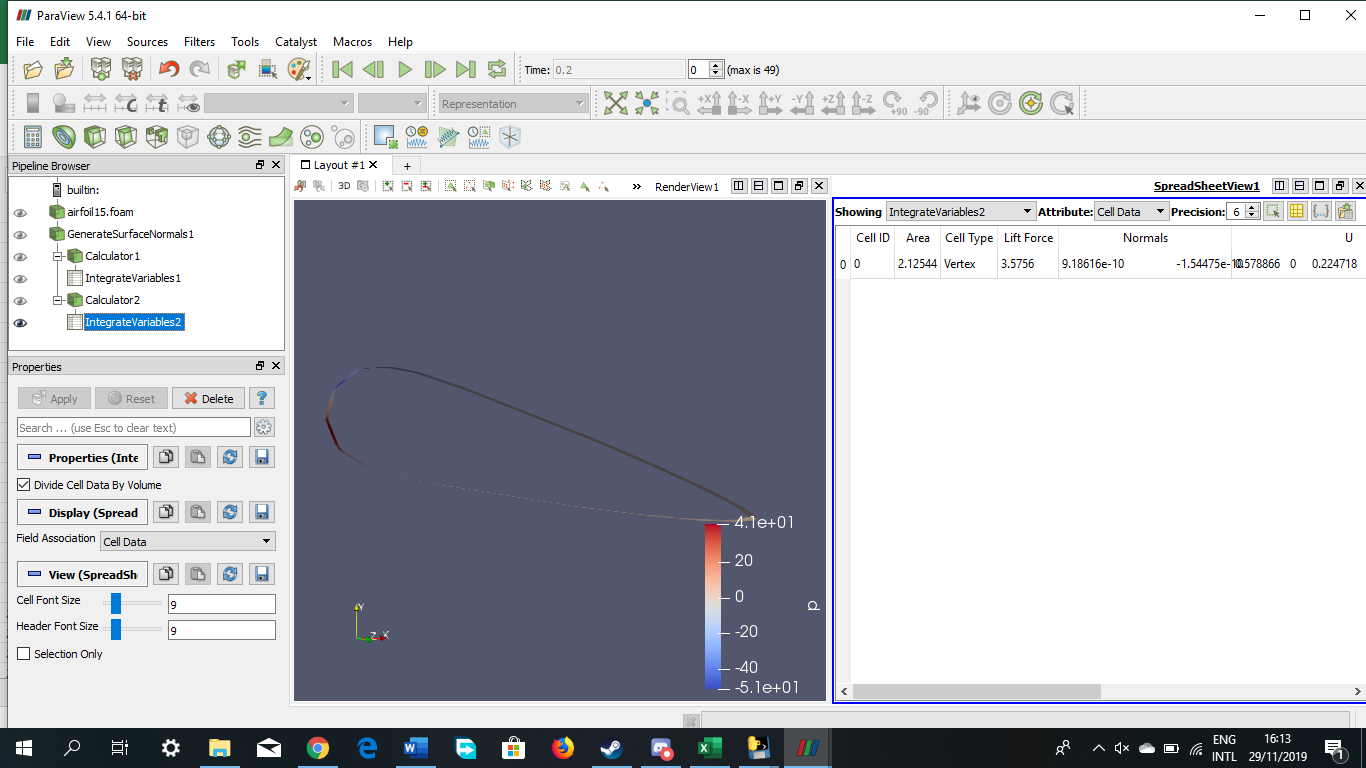
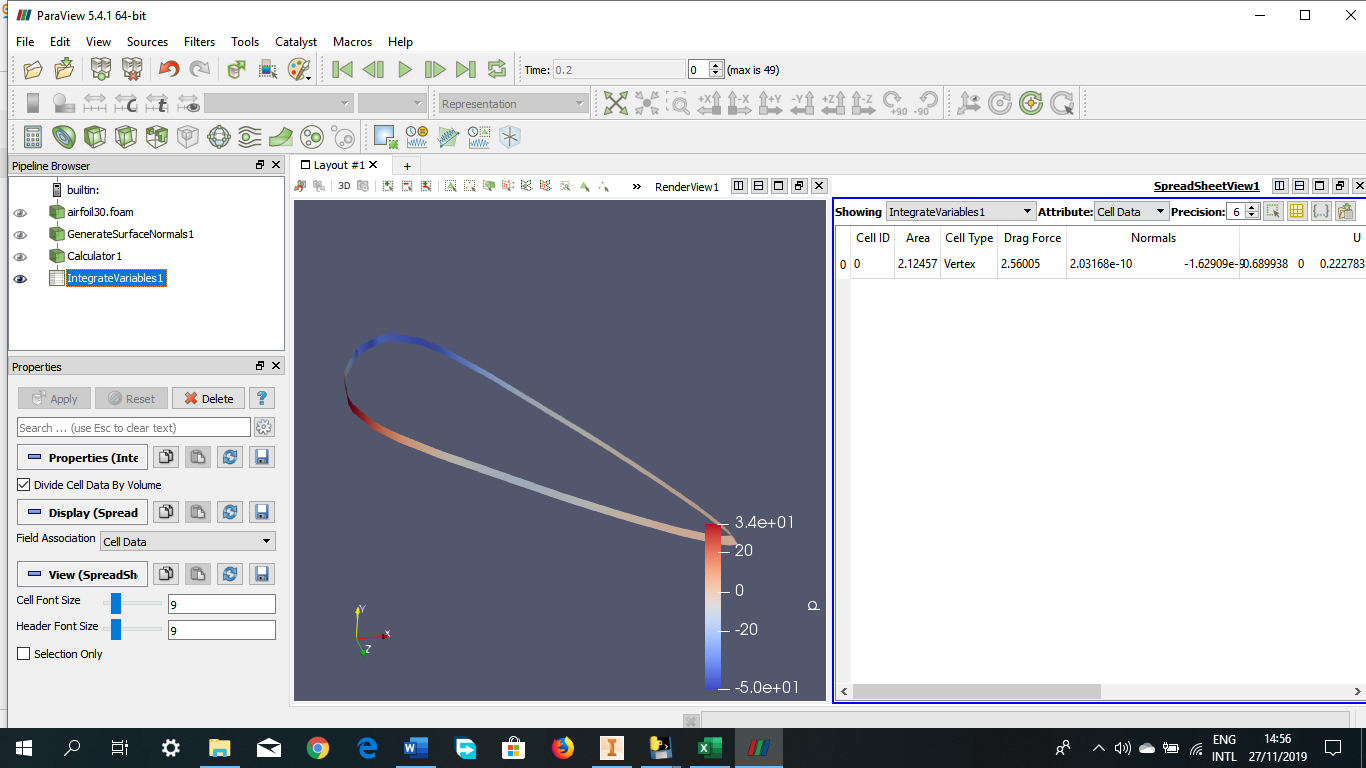
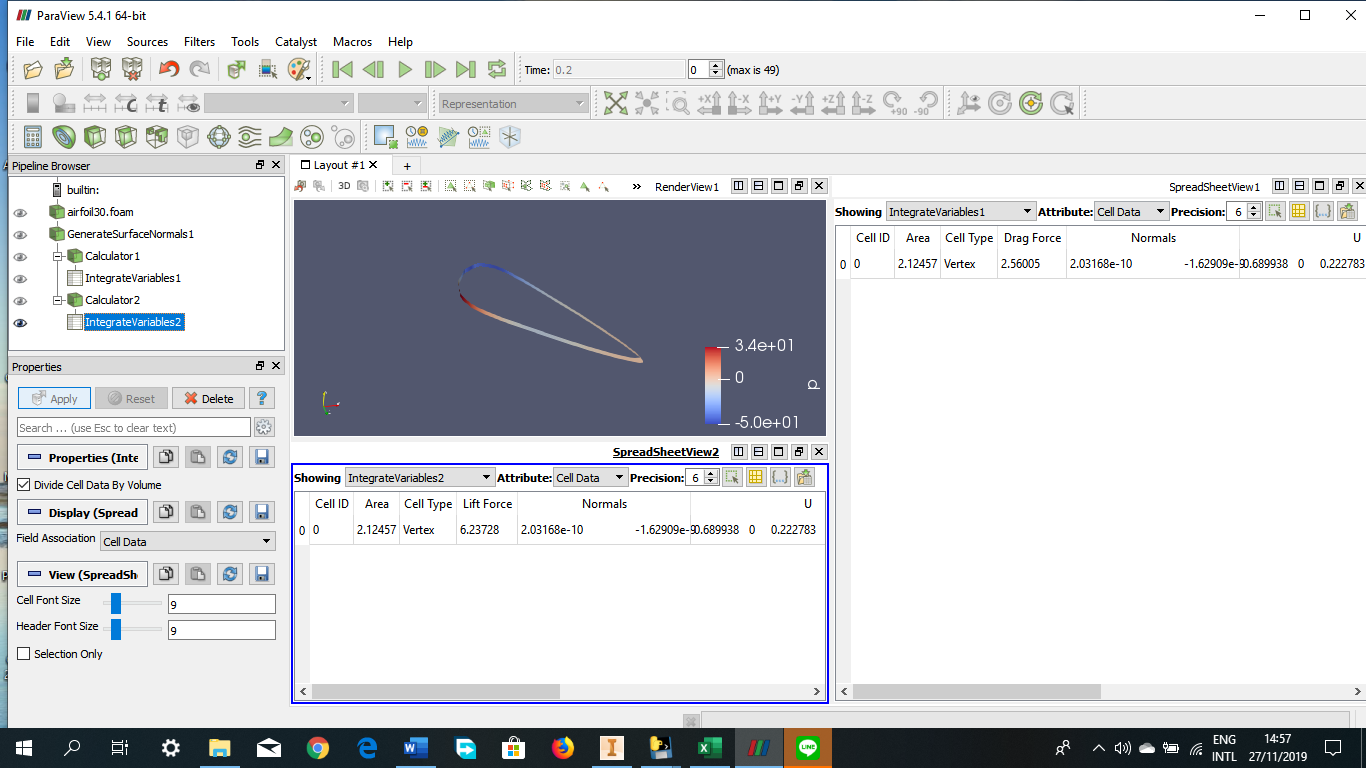
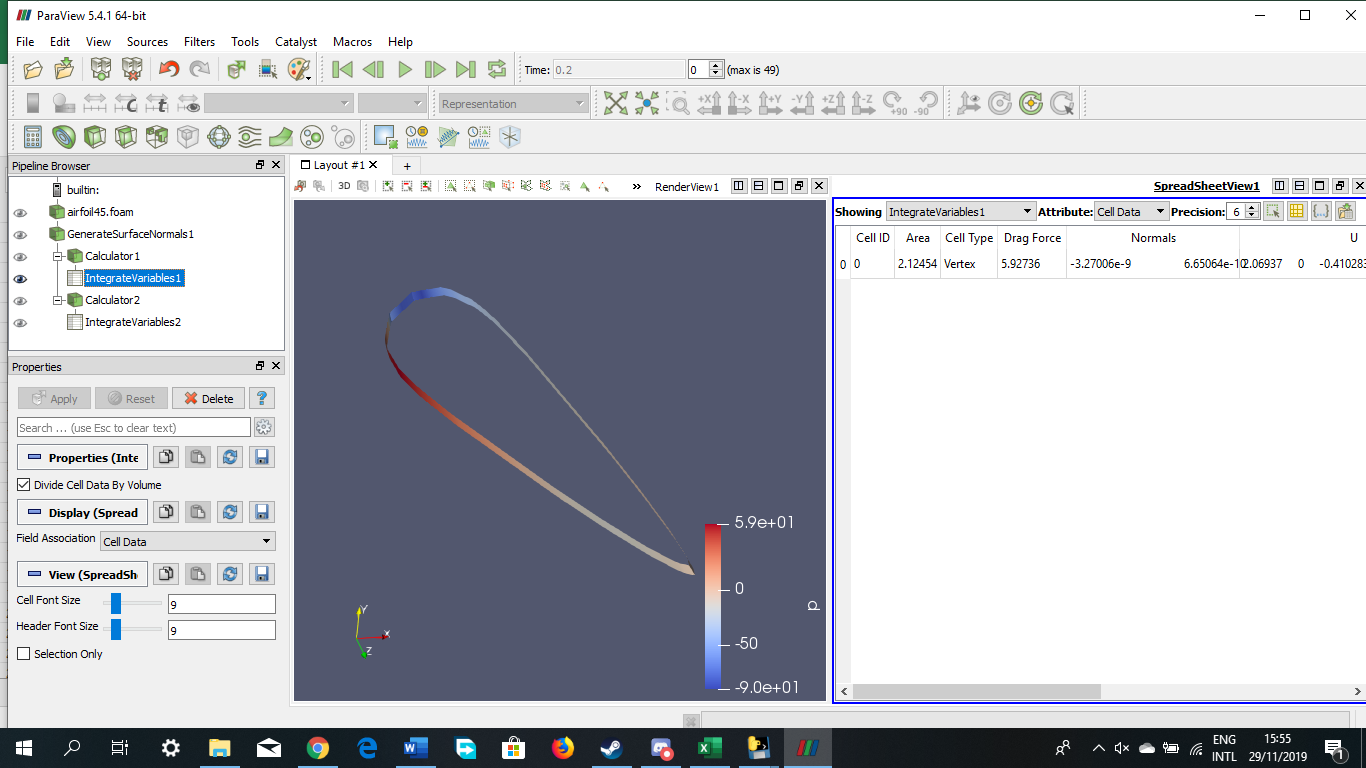
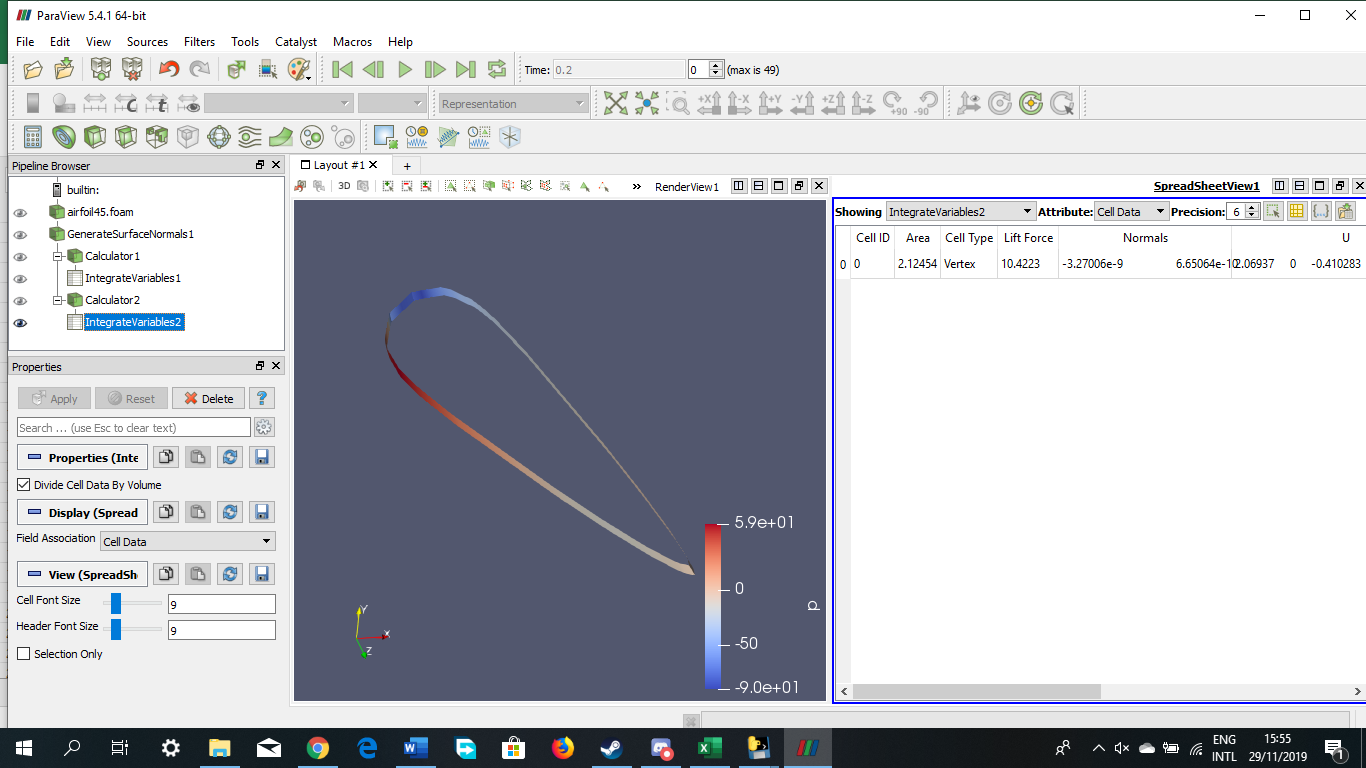
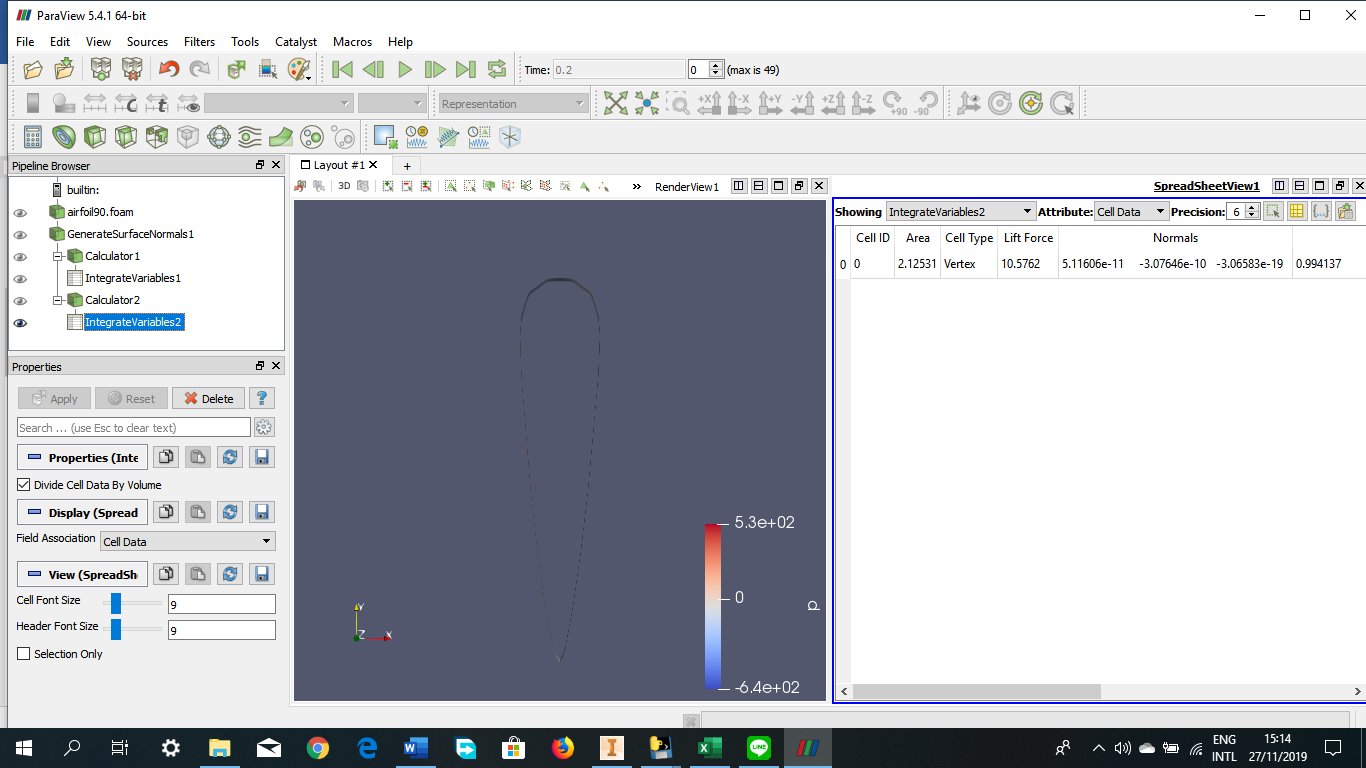
Tugas Analisis Flow pada Airfoil
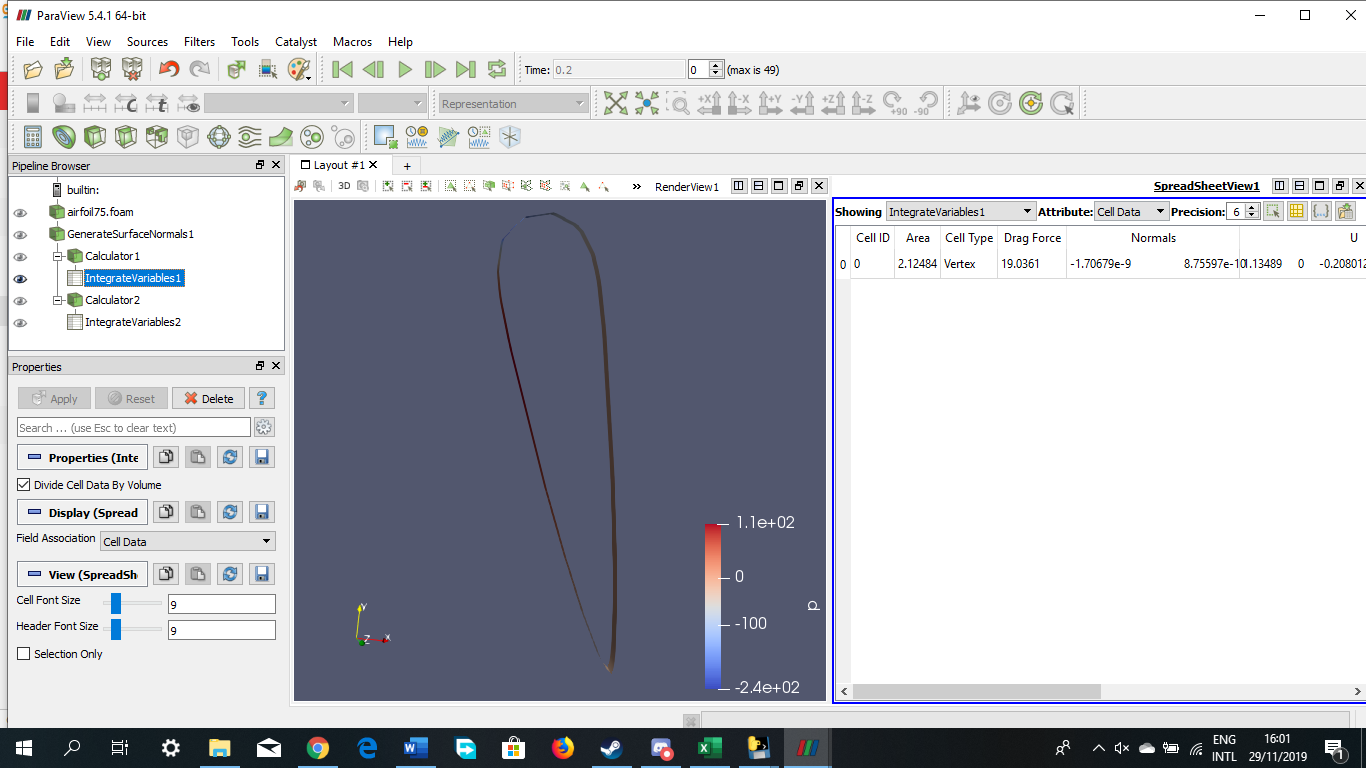
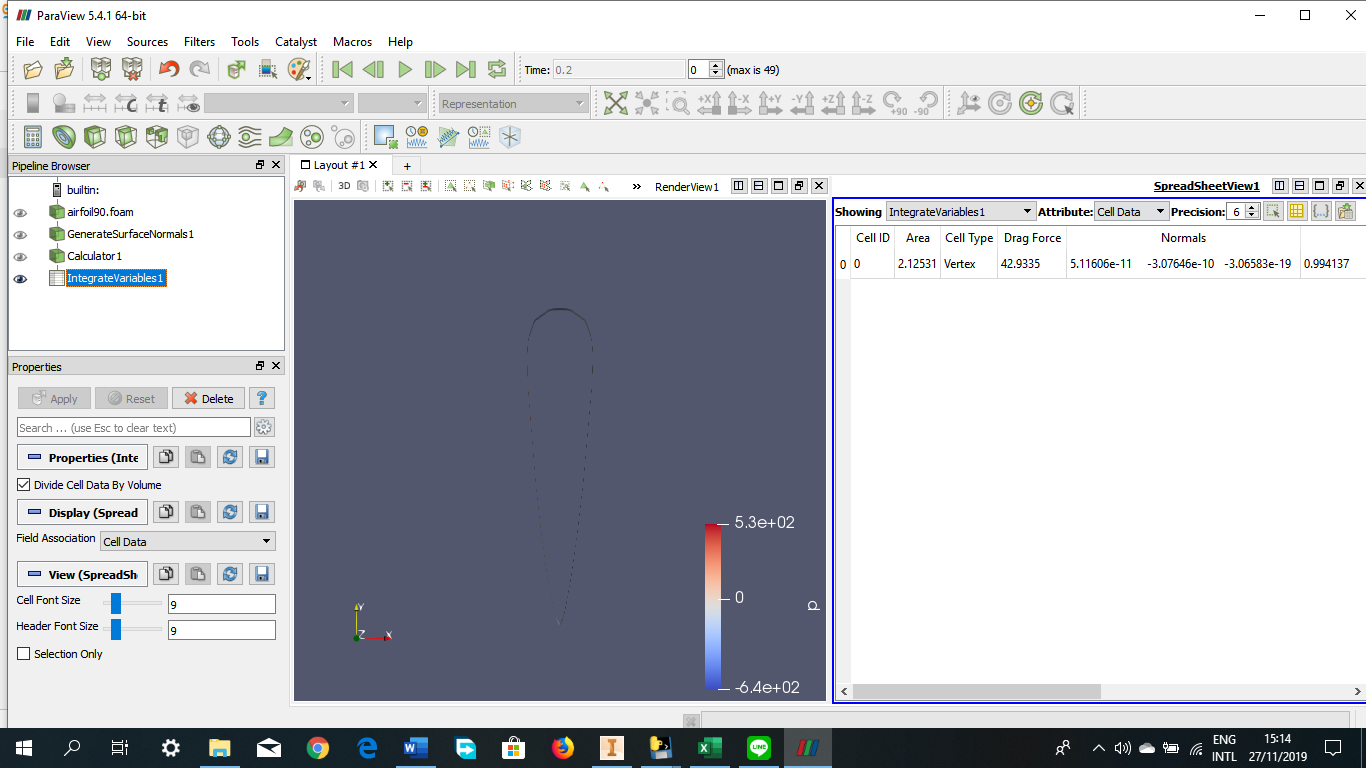
Angle of Attack = -15 derajat
Angle of Attack = 0 derajat
Angle of Attack = 15 derajat
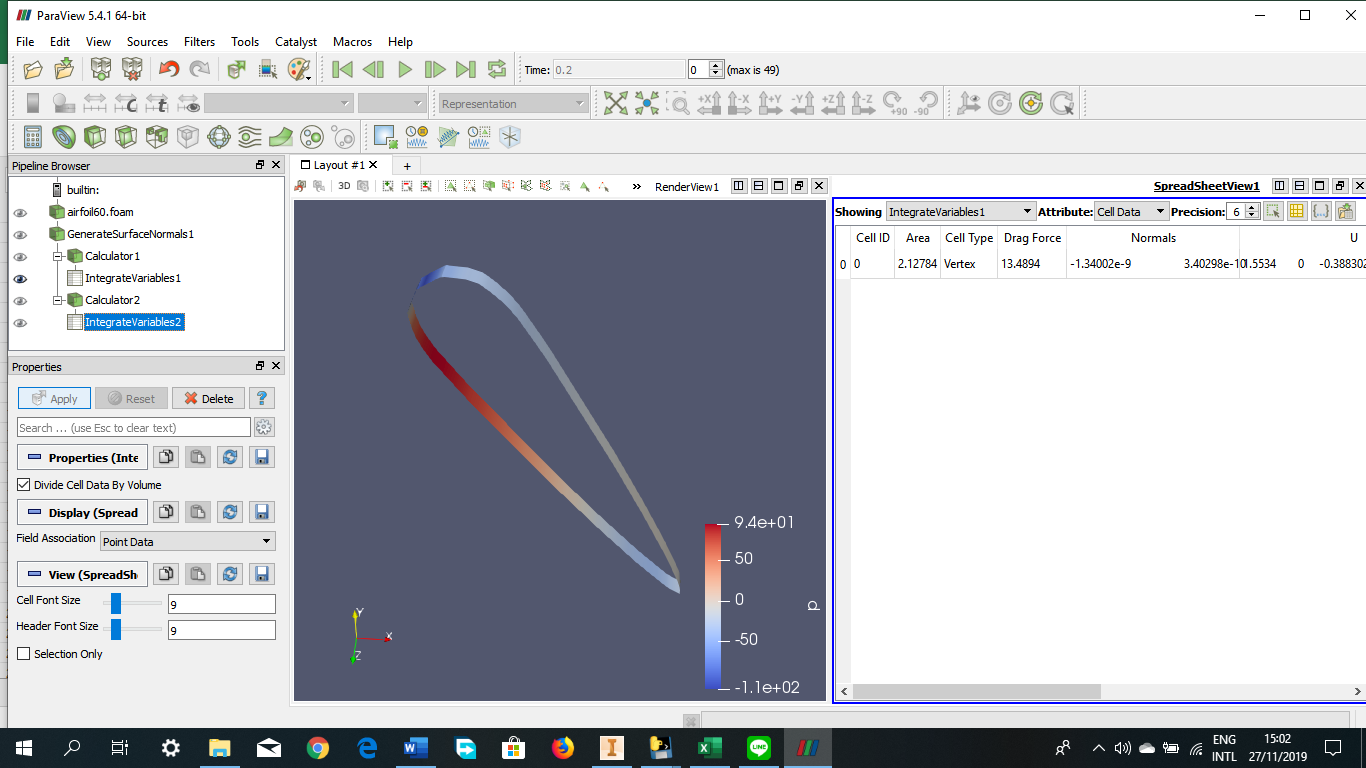
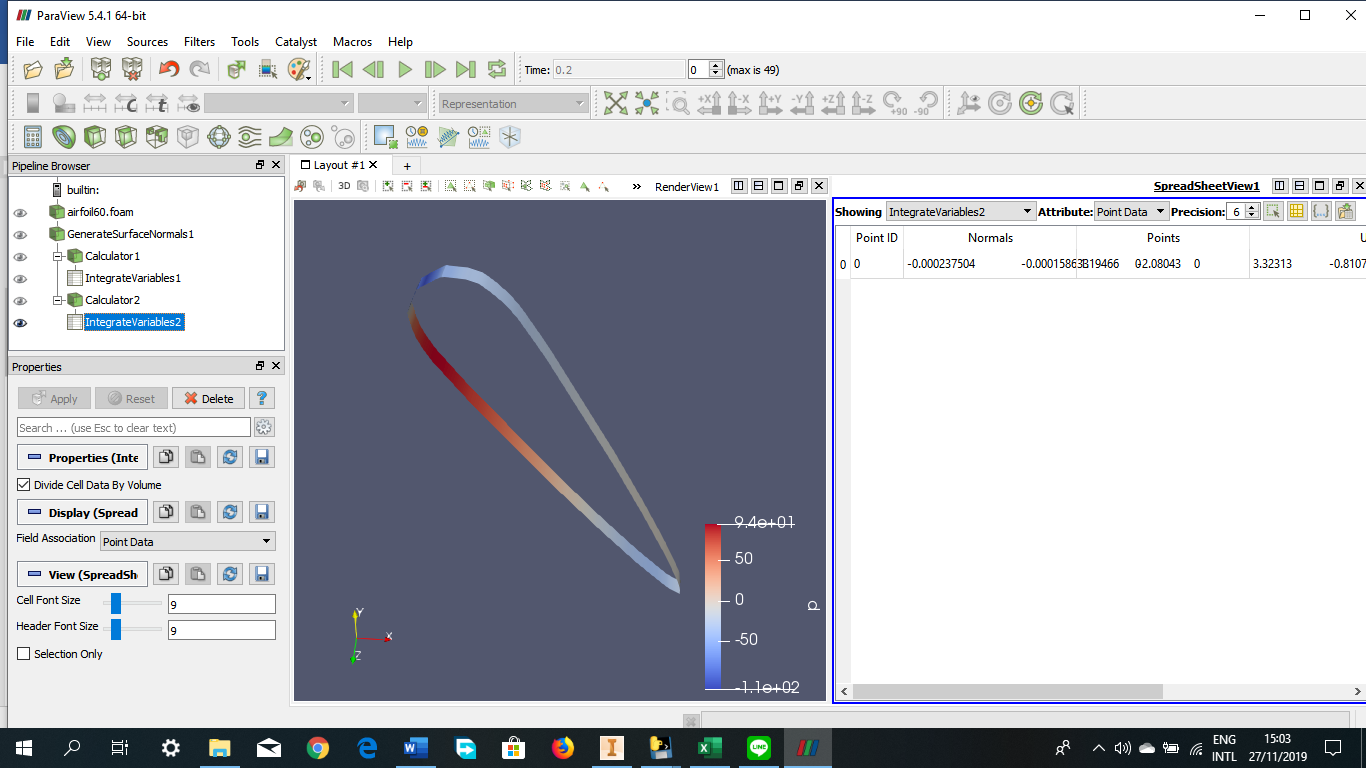
Angle of Attack = 30 derajat
Angle of Attack = 45 derajat
Angle of Attack = 60 derajat
Angle of Attack = 75 derajat
Angle of Attack = 90 derajat
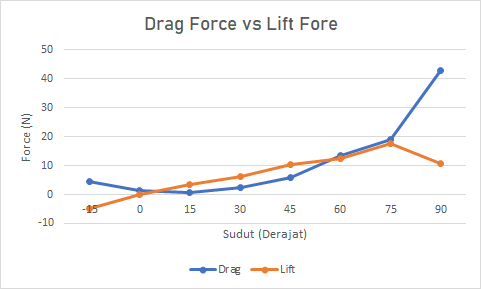
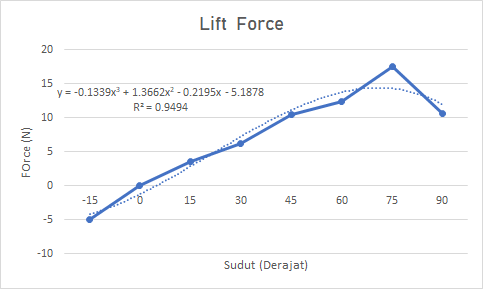
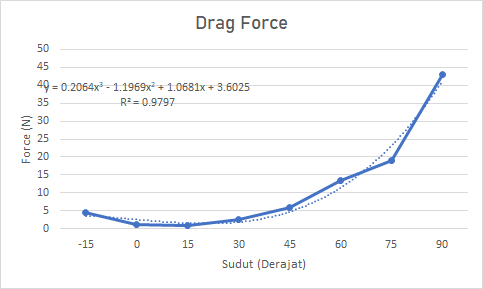
Grafik Optimalisasi menggunakan Excel
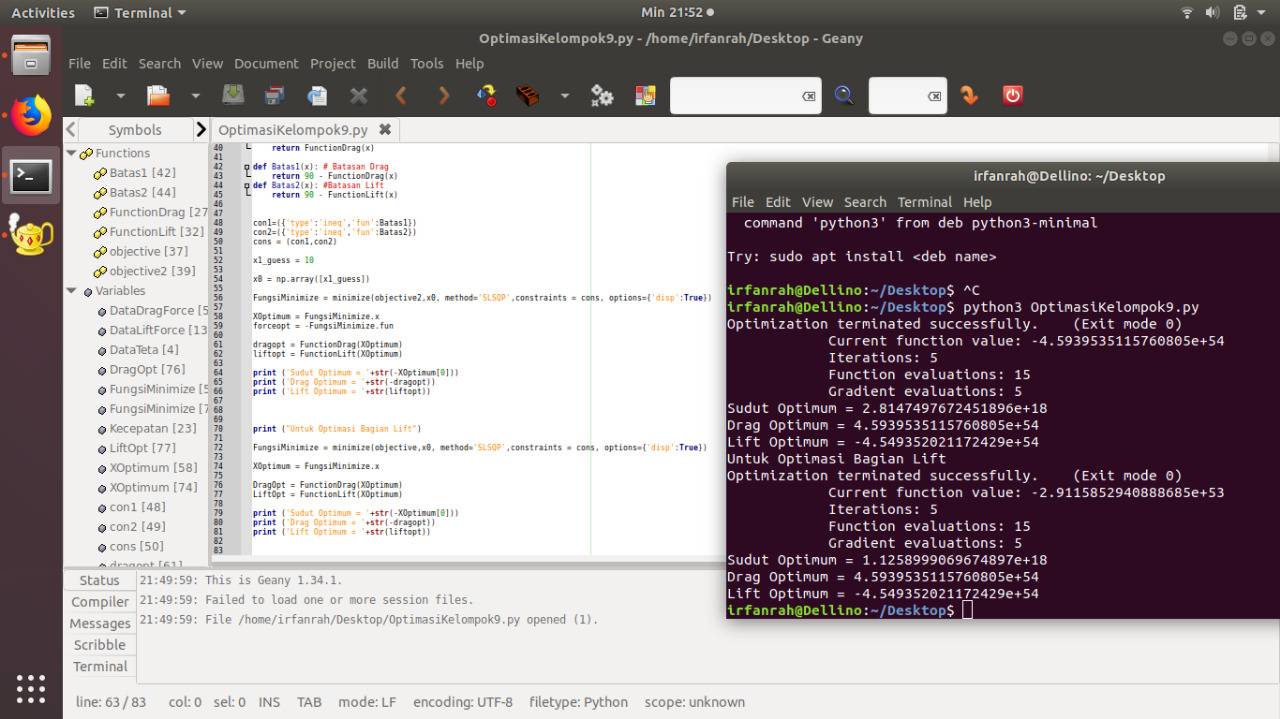
Hasil Optimalisasi menggunakan Python
Artificial Neural Network
ANN adalah adalah model komputasi yang terdiri dari beberapa elemen pemrosesan yang menerima input dan memberikan output berdasarkan fungsi aktivasi yang telah ditentukan.
Step-Step Pembuatan ANN
1. Data Preprocessing
2. Add input layers
3. Random w init
4. Add hidden layers
5. Select optimizer, loss, and performance matrixs
6. compile the model
7. use model .fit to train the model
8. evaluate the model
9. Adjust optimization parameters or model if needed


Enable comment auto-refresher