Hydrogen storage tank for motorcycle

Requirements : Designing hydrogen storage with 1 liter volume that can withstand 8 bar of pressure with limited budget

Design variables : Geometry size, material thickness to strength, material selection

Restrictions : Budget Rp500.000,00

Objectives : Smallest surface area, thinnest material able to withstand 8 bar pressure

Geometry Optimization

The geometry optimization is to minimize the surface area of the hydrogen storage in order to save material needs. The volume of the storage is fix with 1 liter size but could have numerous combination of radius and height. In order to minimize the surface area, using python will help the long work. The solution is provided below:

   pi=22/7
   height = 1000/(pi*radian**2)
   mylist = [] 
   for radian in range (1,16):
       sur_area = ((2*pi*radian) * height) + ((pi*radian**2)*2)
       mylist.append((sur_area,radian))
   print(mylist)

Result:

[(2006.2857142857142, 1), (1025.142857142857, 2), (723.2380952380953, 3), (600.5714285714286, 4), (557.1428571428571, 5), (559.6190476190477, 6), (593.7142857142858, 7), (652.2857142857142, 8), (731.3650793650793, 9), (828.5714285714286, 10), (942.3896103896104, 11), (1071.8095238095239, 12), (1216.131868131868, 13), (1374.857142857143, 14), (1547.6190476190475, 15)]

Ranging from 5 to 6 cm of the radius, we could get the minimum surface area. To have more precise calculation, we'll use smaller range of iteration. Solution is provided below:

   mylist = []
   r = 5
   while True:
      sur_area = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
      mylist.append((sur_area, r)) 
      r += 0.01
      if r > 6:
        break
   print('minimum surface area, radian:', min(mylist))

The Final Result:

(minimum surface area, radian): (553.6553471797575, 5.419999999999991)

Thus the minimum surface area 553.7 cm^2 occurs on radius of 5.42 cm ​

Material Thickness to Strength

The biggest stress in thin wall tube is circumferential stress, so the calculation of the material thickness to the circumferential stress should satisfy its strength in order to ensure the storage is safe. Below are the code to iterate several thickness to required strength:

  r = 5.42e-2
  p = 800000
  t = 1e-3
  mylist = [] 
  while t < 3e-3:
    circumferential = (r * p)/(t)
    t += 0.1e-3
    mylist.append((t,circumferential))
  print('(Thickness, Pressure):',mylist)

The Result (Thickness, Pressure)(m, Pa):

[(0.0011, 43360000.0), (0.0012000000000000001, 39418181.81818181), (0.0013000000000000002, 36133333.33333333), (0.0014000000000000002, 33353846.15384615), (0.0015000000000000002, 30971428.571428567), (0.0016000000000000003, 28906666.66666666), (0.0017000000000000003, 27099999.999999996), (0.0018000000000000004, 25505882.35294117), (0.0019000000000000004, 24088888.888888884), (0.0020000000000000005, 22821052.63157894), (0.0021000000000000003, 21679999.999999996), (0.0022, 20647619.047619045), (0.0023, 19709090.909090906), (0.0024, 18852173.91304348), (0.0024999999999999996, 18066666.666666668), (0.0025999999999999994, 17344000.000000004), (0.0026999999999999993, 16676923.07692308), (0.002799999999999999, 16059259.259259263), (0.002899999999999999, 15485714.285714291), (0.0029999999999999988, 14951724.13793104), (0.0030999999999999986, 14453333.33333334)]

Thus, for thickness 1.1 mm, required material that has 43.4 MPa yield strength. The addition of thickness could lowered required material strength, for thickness 3.1 mm, only required 14.45 MPa yield strength.

The selection of thickness will depend on material selection based on cost and availability in market

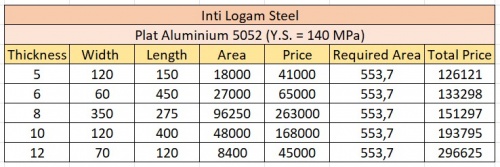
Material Selection

Material selection depends on availability on market. With various choices in market, one of the most suitable choice for hydrogen storage is Aluminium 5052 (AA) that has 140 MPa yield strength with relative affordable price.

With budget Rp 500,000, is far than enough to purchase sufficient strength for the hydrogen storage. But to have the optimal cost to strength, thickness of 8 mm is recommended to be chosen, with cost not far above thickness of 6 mm, but has 33% more strength since engineering aspects require safety factor to prevent material failure during application and usage.