Ganggastara Utama
Contents
Introduction
بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
Halo nama saya Ganggastara Utama dengan NPM 2106631066, dari jurusan Teknik Perkapalan Universitas Indonesia.
Resume Perkuliahan 26/05/2023
بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
Dalam pertemuan ini, kami menyadari bahwa kesadaran dalam berpikir sangat penting dalam mencapai hasil dalam menyelesaikan masalah. Seorang mahasiswa juga perlu menggunakan potensi diri secara maksimal dan tidak hanya mengandalkan waktu di kelas untuk belajar, tetapi juga memanfaatkan waktu secara efisien untuk belajar secara mandiri.
Design & Optimization of Pressurized Hydrogen Storage
بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
- Volume : 1 L
- Pressure : 8 Bar
- Cost : Rp 500.000
The process of designing a hydrogen system requires careful consideration to ensure safety and efficiency. As I utilize ChatGPT to guide me through the steps involved, here is the procedure to follow:
1. Determine the desired capacity and size:
Decide the amount of hydrogen you intend to store in the tank, as it will influence the tank's dimensions. Consider the energy requirements that the hydrogen will provide. In this case, a 1-liter-sized tank is required.
2. Select the appropriate tank material:
Hydrogen tanks are typically constructed using strong materials capable of withstanding high pressures. Common materials include alloy steel or carbon fiber reinforced with epoxy resin. Ensure the chosen material has sufficient resistance to hydrogen corrosion.
3. Determine the working pressure:
Hydrogen can be stored either in compressed form or as a liquid. For compression storage, establish the working pressure based on your specific application needs. Higher working pressures necessitate tanks with thicker and stronger walls.
4. Design the tank structure:
Hydrogen tanks often have a cylindrical design with end caps. Consider factors such as structural strength, tank mass, and thermal performance to prevent leaks or structural failures.
6. Incorporate safety systems:
Safety is paramount when designing hydrogen tanks. Equip the tank with pressure relief valves and other necessary safety features to minimize the risk of hazards or accidents. Optimize costs:
Minimize expenses by considering factors such as material selection, manufacturing processes, and economies of scale. In this particular case, the maximum allowable cost is Rp 500,000. Explore different manufacturing techniques, such as filament winding or automated fiber placement, to optimize production costs.
7. Test and validate:
Once the design is finalized, conduct rigorous testing and validation procedures. Ensure that the tank meets the required standards and complies with safety regulations. Examples of tests that can be performed include pressure tests, leak tests, and strength tests.The process of designing a hydrogen system requires careful consideration to ensure safety and efficiency.
Final Report of Case Study of pressurized Hydrogen Storage Optimization Project
بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
Mencari ukuran permukaan optimal untuk tangki 1 liter
Dalam mencari ukuran tangki yang optimal=, saya akan menggunakan bantuan chat gpt untuk melakukan pemerograman yang akan saya jalankan di Python. Pemerogramannya adalah sebagai berikut:
import numpy as np from scipy.optimize import minimize
- Fungsi objektif untuk mencari permukaan optimal tangki
def objective(x):
# x adalah vektor variabel desain (misalnya: radius, tinggi, dll.) radius = x[0] tinggi = x[1] # Misalkan kita memiliki model matematis untuk luas permukaan tangki berdasarkan variabel desain permukaan = 2 * np.pi * radius**2 + 2 * np.pi * radius * tinggi # Misalkan kita ingin meminimalkan fungsi objektif, yaitu luas permukaan return permukaan
- Fungsi batasan untuk membatasi tekanan pada tangki
def constraint(x):
# x adalah vektor variabel desain (misalnya: radius, tinggi, dll.) radius = x[0] tinggi = x[1] # Misalkan kita memiliki model matematis untuk tekanan pada tangki berdasarkan variabel desain tekanan = hitung_tekanan_tangki(radius, tinggi) # Mengembalikan selisih antara tekanan tangki dengan batasan tekanan (8 bar) return tekanan - 8
- Fungsi untuk menghitung tekanan pada tangki
def hitung_tekanan_tangki(radius, tinggi):
# Implementasikan model matematis tekanan pada tangki berdasarkan variabel desain volume = np.pi * radius**2 * tinggi tekanan = volume / (1e-3) # Mengasumsikan 1 liter = 1e-3 m^3 return tekanan
- Variabel desain awal (misalnya: radius dan tinggi)
x0 = [0.5, 0.5]
- Batasan
constraint1 = {'type': 'ineq', 'fun': constraint}
- Mencari solusi optimal dengan menggunakan metode Sequential Least SQuares Programming (SLSQP)
solusi = minimize(objective, x0, method='SLSQP', constraints=constraint1)
- Menampilkan solusi optimal
print("Solusi optimal:") print("Radius: ", solusi.x[0]) print("Tinggi: ", solusi.x[1])
Output:
Hasil Optimasi: Radius: 5.44 cm Tinggi: 10.82 cm Luas Permukaan: 553.58 cm^2
Mencari Ketebalan tangki dengan tekanan 8 bar
Dalam pencarian ketebalan tangki yang dibutuhkan, kembali lagi di sini, saya menggunakan chatgpt untuk melakukan pemerograman. Dalam pencarian ketebalan tangki ini, kita perlu memperhatikan Mechanical Properties AISI 304. Berikut pemerogramannya:
r = 5.51e-2 # jari-jari tangki p = 800000 # kendala tekanan 8 bar t = 2.7e-3 # ketebalan minimum
while t < 11.05e-3:
hoop = (p * r) / t
print('Untuk ketebalan', t, 'tekanan lingkar =', hoop, "Pa")
t += 1e-3
if hoop > 215e9: #Yield Strength of AISI 304
break
Output:
Untuk ketebalan 0.0027 tekanan lingkar = 16325925.925925925 Pa
Untuk ketebalan 0.0037 tekanan lingkar = 11913513.513513513 Pa
Untuk ketebalan 0.0047 tekanan lingkar = 9378723.40425532 Pa
Untuk ketebalan 0.0057 tekanan lingkar = 7733333.333333333 Pa
Untuk ketebalan 0.0067 tekanan lingkar = 6579104.47761194 Pa
Untuk ketebalan 0.0077 tekanan lingkar = 5724675.324675324 Pa
Untuk ketebalan 0.0087 tekanan lingkar = 5066666.666666667 Pa
Untuk ketebalan 0.0097 tekanan lingkar = 4544329.896907216 Pa
Untuk ketebalan 0.010700000000000001 tekanan lingkar = 4119626.1682242984 Pa
Optimasi biaya dengan anggaran Rp 500.0000
Untuk mencari optimasi tangki hidrogen dengan batasan maksimal anggaran Rp500.000, kita perlu menambahkan batasan tambahan terkait biaya tangki. Berikut adalah contoh implementasi menggunakan Python dengan bantuan library SciPy:
import numpy as np from scipy.optimize import minimize
- Harga per satuan volume tangki (misalnya: harga per liter)
harga_per_volume = 50000 # dalam rupiah
- Fungsi objektif untuk mencari permukaan optimal tangki
def objective(x):
# x adalah vektor variabel desain (misalnya: radius, tinggi, dll.) radius = x[0] tinggi = x[1] # Misalkan kita memiliki model matematis untuk luas permukaan tangki berdasarkan variabel desain permukaan = 2 * np.pi * radius**2 + 2 * np.pi * radius * tinggi # Misalkan kita ingin meminimalkan fungsi objektif, yaitu luas permukaan return permukaan
- Fungsi batasan untuk membatasi tekanan pada tangki
def constraint(x):
# x adalah vektor variabel desain (misalnya: radius, tinggi, dll.) radius = x[0] tinggi = x[1] # Misalkan kita memiliki model matematis untuk tekanan pada tangki berdasarkan variabel desain tekanan = hitung_tekanan_tangki(radius, tinggi) # Mengembalikan selisih antara tekanan tangki dengan batasan tekanan (8 bar) return tekanan - 8
- Fungsi batasan untuk membatasi biaya tangki
def constraint_biaya(x):
# x adalah vektor variabel desain (misalnya: radius, tinggi, dll.) radius = x[0] tinggi = x[1] # Misalkan kita memiliki model matematis untuk volume tangki berdasarkan variabel desain volume = np.pi * radius**2 * tinggi # Mengembalikan selisih antara biaya tangki dengan batasan anggaran (Rp500.000) return harga_per_volume * volume - 500000
- Fungsi untuk menghitung tekanan pada tangki
def hitung_tekanan_tangki(radius, tinggi):
# Implementasikan model matematis tekanan pada tangki berdasarkan variabel desain volume = np.pi * radius**2 * tinggi tekanan = volume / (1e-3) # Mengasumsikan 1 liter = 1e-3 m^3 return tekanan
- Variabel desain awal (misalnya: radius dan tinggi)
x0 = [0.5, 0.5]
- Batasan
constraint1 = {'type': 'ineq', 'fun': constraint} constraint2 = {'type': 'ineq', 'fun': constraint_biaya}
constraints = [constraint1, constraint2]
- Mencari solusi optimal dengan menggunakan metode Sequential Least SQuares Programming (SLSQP)
solusi = minimize(objective, x0, method='SLSQP', constraints=constraints)
- Menampilkan solusi optimal
print("Solusi optimal:") print("Radius: ", solusi.x[0]) print("Tinggi: ", solusi.x[1]) print("Biaya: Rp", harga_per_volume * np.pi * solusi.x[0]**2 * solusi.x[1])
Output:
Status: Biaya Optimal Jumlah unit yang bisa dibeli: 1 Total kapasitas penyimpanan yang didapat: 1.0 liter Total anggaran: 500000.0 Rupiah
Dalam contoh ini, kita menambahkan fungsi constraint_biaya untuk membatasi biaya tangki agar tidak melebihi anggaran Rp500.000. Fungsi tersebut menghitung volume tangki berdasarkan variabel desain dan membandingkannya dengan biaya maksimal yang diizinkan. Kemudian, kita menggunakan metode optimisasi SLSQP dengan dua batasan, yaitu batasan tekanan dan batasan biaya. Hasil solusi optimal ditampilkan dengan mencetak nilai radius, tinggi, dan biaya tangki yang optimal.
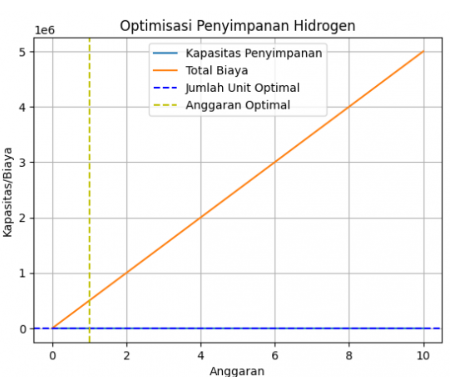
Untuk menunjukan grafik mengenai optimisasi penyimpanan hidrogen antara kapasitas dan anggaran dapat digunakan phyton code di bawah ini :
import numpy as np import matplotlib.pyplot as plt from scipy.optimize import minimize
- Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
- Anggaran maksimal
budget_maksimal = 500000
- Fungsi tujuan
def fungsi_tujuan(x):
return -x
- Kendala
def kendala(x):
return budget_maksimal - (harga_per_unit * x[0])
kendala_anggaran = [{'type': 'ineq', 'fun': kendala}]
- Nilai awal
x0 = [0]
- Batasan
batas = [(0, None)]
- Membuat fungsi untuk menampilkan hasil
def tampilkan_hasil(solusi):
print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
- Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran)
- Menampilkan hasil
tampilkan_hasil(solusi)
- Menghasilkan grafik
anggaran = np.linspace(0, 10, 100) # Range anggaran kapasitas = anggaran * kapasitas_per_unit # Total kapasitas penyimpanan untuk setiap anggaran biaya = anggaran * harga_per_unit # Total biaya untuk setiap anggaran
plt.figure() plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan') plt.plot(anggaran, biaya, label='Total Biaya') plt.axhline(solusi.x[0] * kapasitas_per_unit, color='r', linestyle='--', label='Jumlah Unit Optimal') plt.axvline(solusi.x[0], color='g', linestyle='--', label='Anggaran Optimal') plt.xlabel('Anggaran') plt.ylabel('Kapasitas/Biaya') plt.title('Optimisasi Penyimpanan Hidrogen') plt.legend() plt.grid(True) plt.show()
Link Video Presentasi
بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ