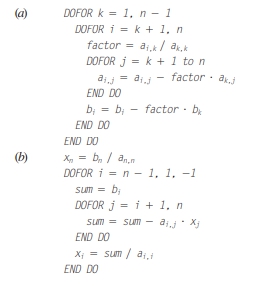Fakhri Hawari Muhammad
Nama saya Fakhri Hawari Muhammad. Saya biasa dipanggil fakhri atau hawari oleh teman-teman saya. Saya adalah mahasiswa teknik mesin universitas indonesia angkatan 2018. Saat ini saya berdomisili di Kota Depok. Saat ini saya sudah memasuki semester ke-5 dalam studi S-1 saya. Saya memilih teknik mesin karena saya rasa ilmu yang dipelajari teknik mesin akan terus digunakan dimasa mendatang dan dapat berkembang lebih luas.
Selama setengah semester di mata kuliah metode numerik ini, saya telah belajar mengenai turunan numerik, interpolasi, regresi, beberapa metode untuk mencari akar persamaan, dan juga diperkenalkan untuk membuat pseudocode.
Tujuan dari mata kuliah metode numerik ini antara lain adalah sebagai berikut,
- Memahami konsep dan prinsip dasar dalam Metode Numerik
- Dapat menerapkan pemahaman dari konsep yang ada di dalam permodelan numerik
- Mampu menerapkan Metode Numerik dalam persoalan engineering
- Mendapat nilai tambah (suatu value/ nilai moral) terhadap diri masing-masing
Contents
[hide]Pertemuan 1 (11/11/2020)
Pada kuliah 11 November 2020, Saya mempelajari dari penjelasan dan diskusi yang ada mengenai beberapa hal. Pertama, saya memahami bahwasanya dalam pembelajaran, apapun itu, kita seharusnya bukan saja memahami apa yang harus dipahami, tetapi juga harus mengetahui apa yang tidak kita pahami. Dengan begitu, kita dapat mengerti apa yang kurang dari diri kita dan menjadi refleksi diri serta memacu rasa ignin tahu. Kemudian dari contoh limit perhitungan di sebuah software, saya memahami bahwa secanggih apapun komputer tetap lebih pintar manusia dibaliknya karena komputer dan softwarenya hanyalah sebuah alat bantu. Saya juga memahami bahwa dengan adanya limit tersebut, seharusnya kita sebagai manusia bisa memanfaatkan peluang yang ada sebaik-baiknya. Jika software tersebut mencapai limit tertentu maka maksimalkanlah kemampuan komputer tersebut. Lalu saya juga memahami bahwa manusiapun ada limitnya, seperti 1/0 yang manusia tidak dapat mendefinisikannya. Maka yang tahu hanyalah tuhan sehingga sejatinya kita sebagai manusia tidaklah pantas untuk memisahkan ilmu pengetahuan dengan ketuhanan.
Tugas 1
- Pada tugas pertama ini, Pak Dai meminta untuk mempelajari OpenModelica, kemudian memberikan penjelasan video terkait apa yang sudah dipelajari. Berikut video dari saya:
Pertemuan 2 (18/11/2020)
Pada Kuliah 18 November 2020, perkuliahan diawali dengan review mengenai tugas 1 dan apa saja yang dipelajari seminggu sebelumnya. Kemudian dijelaskan mengenai software openmodelica. Dibandingkan dengan program seperti python,c++,dsb, openmodelica cendrung lebih ke arah program permodelan, bukan program murni coding sehingga sangat cocok untuk menyelesaikan permasalahan-permasalahan yang berhubungan dengan dunia engineering. Openmodelica memiliki kekurangan yaitu ketika mensimulasikan akan cendrung lebih lama, hal ini disebabkan openmodelica harus menerjemahkan dari bahasa permodelan ke bahasa coding, kemudian ke bahasa mesin. Kemudian dijelaskan juga dasar-dasar openmodelica, seperti perbedaan 'parameter real', 'real', spesialisasi program, dan dijelaskan juga secara ringkas bagaimana contohnya untuk memanggil sebuah persamaan dari program fungsi ke program kelas. Selain itu, dari penjelasan teman-teman lainnya juga dipaparkan bahwa openmodelica juga banyak menyelesaikan permasalahan di sistem kontrol sebagaimana yang saya sebutkan di tugas 1. Di akhir kelas, bang Edo memberi sedikit penjelasan bahwa di openmodelica sebenernya sudah ada beberapa program yang sudah di rumuskan di library sehingga mempermudahkan kita untuk menyelesaikan persoalan, hanya memasukan inputnya saja.
Tugas 2
- Pada tugas ini, Pak Dai meminta untuk mencoba menyelesaikan persamaan aljabar simultan dengan openmodelica dan dengan cara memanggil sebuah fungsi ke sebuah class. Persamaan yang saya gunakan pada kali ini saya dapat dari internet, yaitu:
Lalu untuk video penjelasannya dapat dilihat dibawah ini,
Pertemuan 3 (25/11/2020)
Pada kuliah 25 November 2020, Sebagian besar waktu perkuliahan digunakan untuk sharing mengenai fungsi array oleh saudara Josiah dan terkait pembuatan program Eliminasi Gauss Jordan (dengan membuat fungsi sendiri) oleh saudara Christo. Kemudian dilanjutkan oleh penjelasan oleh Pak Dai mengenai penyelesaian permasalahan engineering. Dalam kasus realnya, ketika kita berhadapan dengan permasalahan engineering kita harus melakukan analisis permasalahan tersebut. Kemudian dari situ kita dapat membuat model matematisnya, sehingga dilangkah selanjutnya kita dapat menyelesaikannya dengan metode numerik untuk mempermudah penyelesaian. Selain itu saya dan yang lainnya juga diminta untuk mencoba menyelesaikan persoalaan yand ada di buku chapra dengan pseudocode yang sudah diberikan seperti berikut:
Untuk algoritma EGJ tersebut, saya sudah memahami dan bisa menerjemahkannya ke bahasa modelica, tetapi saya masih belum paham untuk pemrograman model keseluruhannya. Berikut pseudocode penyelesaian EGJ diatas ketika diubah ke bahasa modelica: // Forward Elimination
for k in 1:(n-1) loop
for i in (k+1):n loop
factor := a[i,k] / a[k,k];
for j in (k+1):n loop
a[i,j] := a[i,j] - (factor * a[k,j]);
end for;
b[i] := b[i] - (factor * b[k]);
end for;
end for;
// Back Substitution
x[n] := b[n] / a[n,n];
for i in (n-1):(-1) loop
sum := b[i];
for j in (i+1):n loop
sum := sum - (a[i,j] * x[j]);
end for;
x[i] := sum / a[i,i];
end for;
Tugas 3
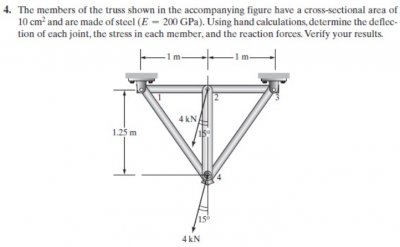
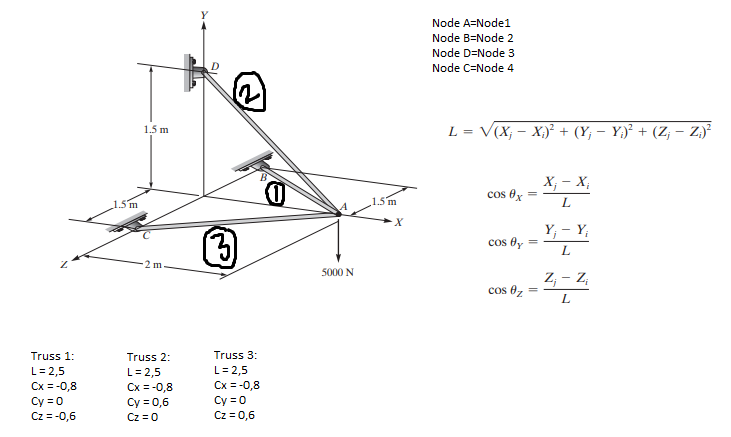
- Berikut adalah soal untuk tugas kali ini:
- Penyelesaian:
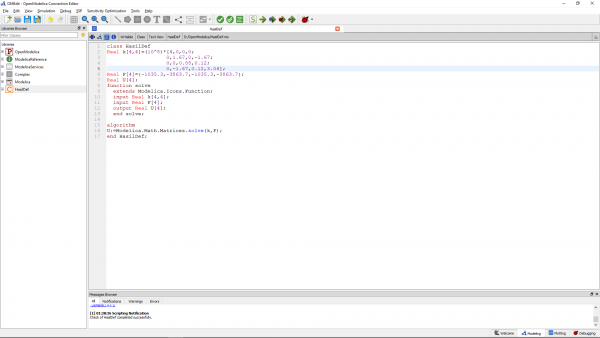
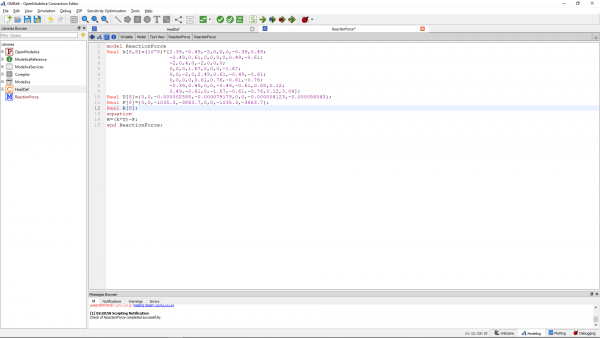
Kemudian untuk penyelesaian matriks diatas (mencari defleksi) dapat diselesaikan dengan OpenModelica. Berikut program yang saya buat:
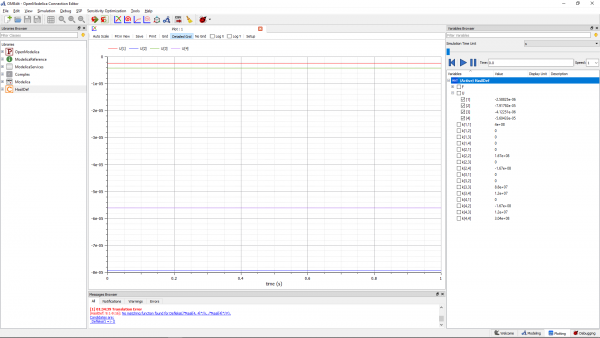
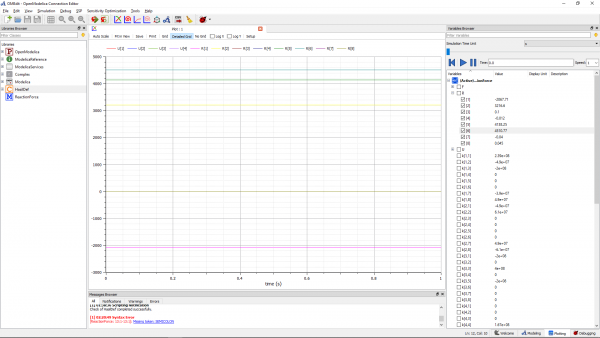
Lalu didapatkan hasil defleksinya (U) seperti yang tertera dibawah ini:
Selanjutnya adalah mencari Gaya-gaya reaksi yang terjadi di tiap node. Berikut adalah persamaan yang dapat digunakan:
Lalu saya membuat programnya di Modelica seperti dibawah ini:
Sehingga setelah dilakukan simulasi, didapatkan hasil (Gaya Reaksi tiap node) sebagai berikut:
Pertemuan 4 (02/12/2020)
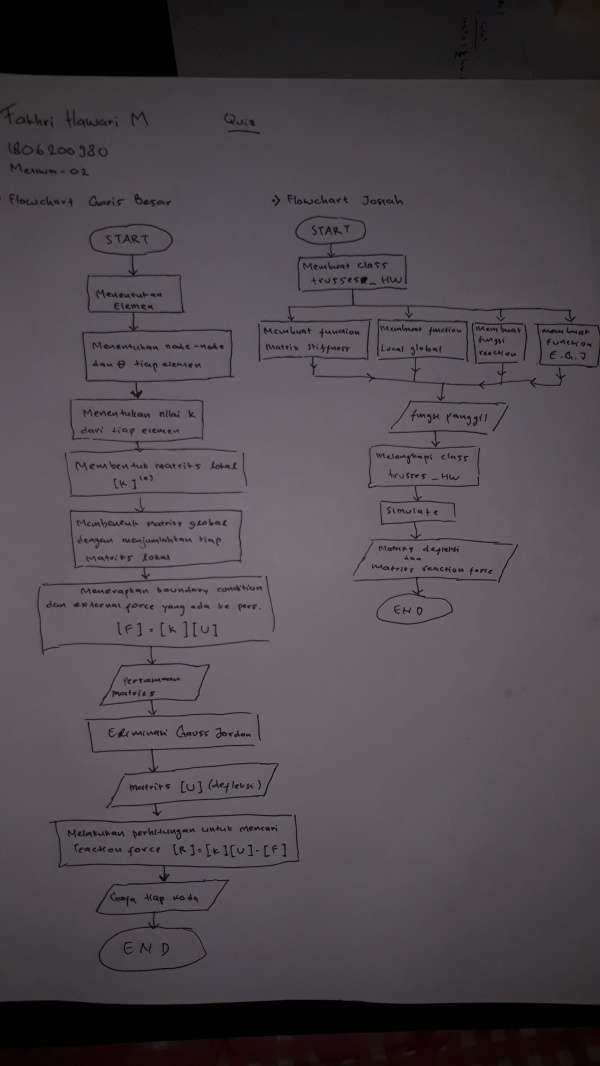
Quiz Diagram Class dan Flow Chart
Tugas 4
- Pada tugas kali ini, diminta untuk menyelesaikan persoalan berikut:
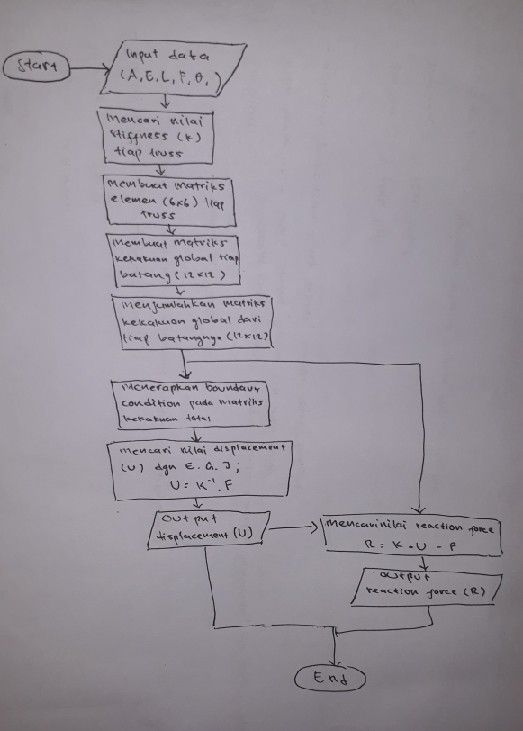
Flowchart:
Berikut video penjelasan penyelesaiannya:
Pertemuan 5 (14/12/2020)
Pertemuan ini merupakan pengganti dari minggu sebelumnya yang kelas ditiadakan karena libur. Pada pertemuan ini lebih ke arah review mengenai penyelesaian space Trusses dan juga mulai di briefing singkat mengenai tugas besar dan materi optimasi oleh pak Dai.
Pertemuan 6 (16/12/2020)
Aplikasi Metode Numerik dalam kasus optimasi. Pada pertemuan ini dikenalkan dengan contoh sederhana terkait optimasi oleh Bu Chandra, yaitu bracket optimization dengan metode golden ratio. Prinsip dari metode ini kurang lebih mirip dengan metode Bisection yang nantinya dilakukan perhitungan berulang-ulang (itterative). Berikut adalah contoh coding di modelica untuk metode golden ratio:
FungsiObjek.mo
function FungsiObjek input Real x; output Real y; algorithm y:= 2*Modelica.Math.sin(x)-x^2/10; end FungsiObjek;
Dimana fungsi ini akan menjadi sebuah fungsi yang ada dipanggil dengan file jenis model.
BracketOptimal.mo
model BracketOptimal
parameter Integer n = 8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
Real d;
algorithm
xup := 4;
xlow := 0;
for i in 1:n loop
d:=((5^(1/2)-1)/2) * (xup-xlow);
x1[i] := xlow+d;
x2[i] := xup-d;
f1[i] := FungsiObjek(x1[i]);
f2[i] := FungsiObjek(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow := x2[i];
xopt := xup;
yopt := f1[i];
else
xlow :=xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end BracketOptimal;
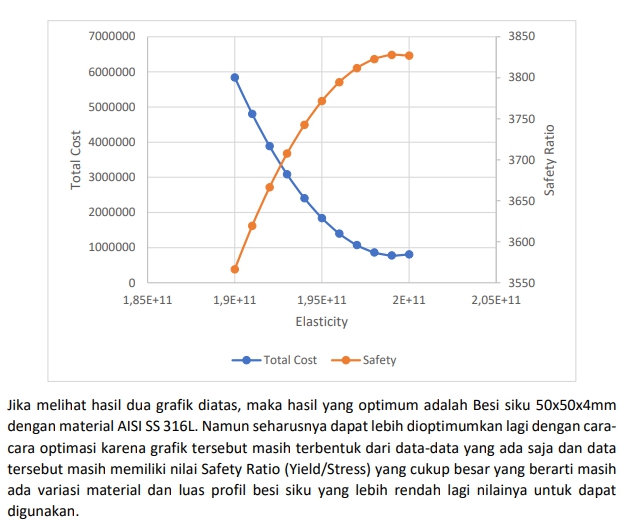
Tugas Besar
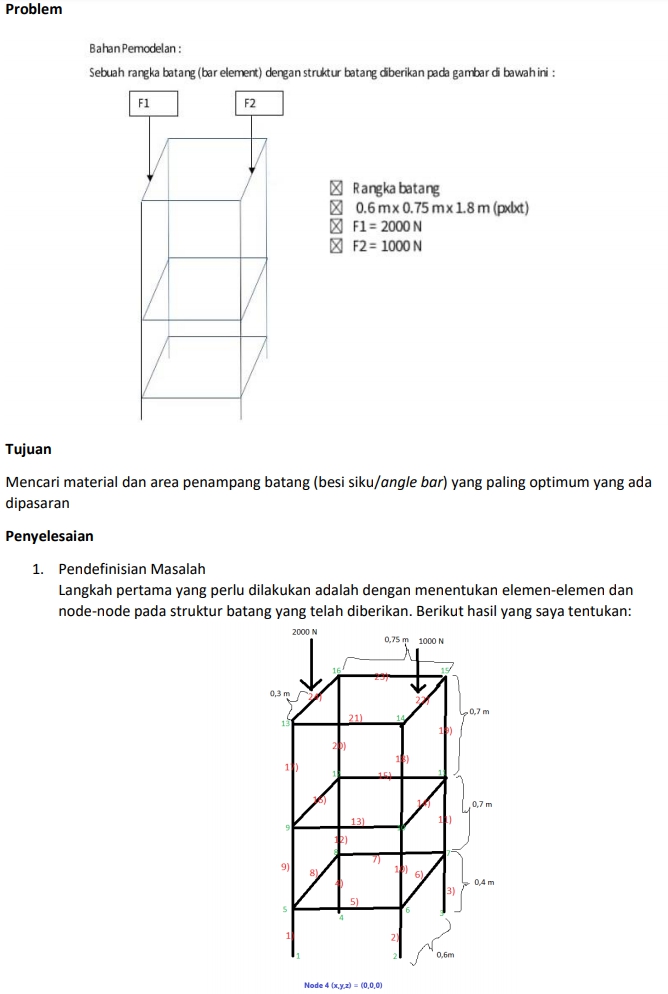
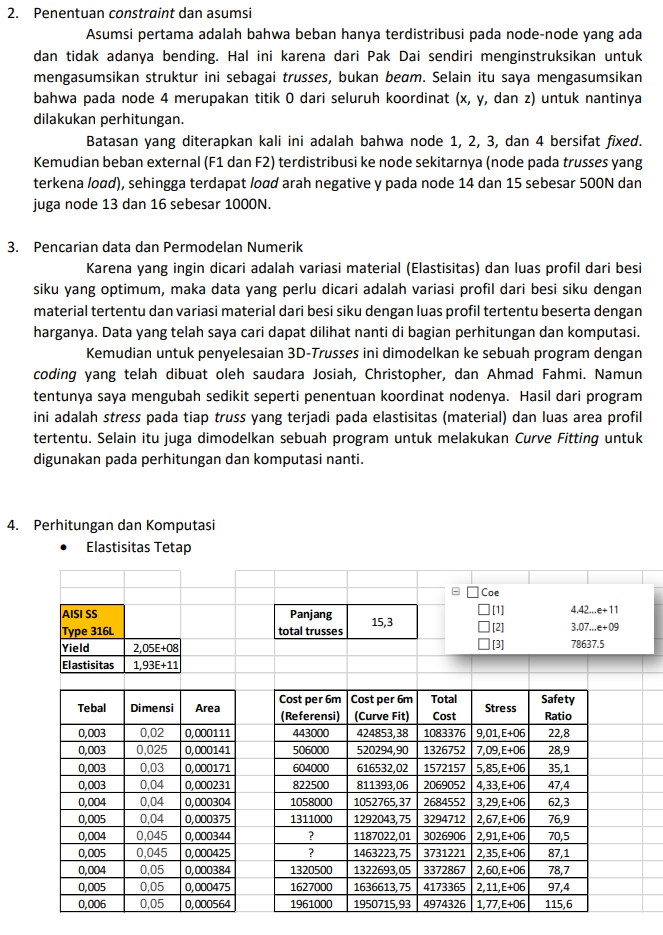
Tema: Optimasi Struktur Batang 3D
Program Pendukung
- Trusses 3D (mencari stress)
model Trusses_Tubes
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa)
parameter Real Area= (nilai area) ; //Luas Penampang Siku (m2)
parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa)
//define connection
parameter Integer C[:,2]=[ 1,5; // (1)
2,6; // (2)
3,7; // (3)
4,8; // (4)
5,6; // (5)
6,7; // (6)
7,8; // (7)
5,8; // (8)
5,9; // (9)
6,10; // (10)
7,11; // (11)
8,12; // (12)
9,10; // (13)
10,11;// (14)
11,12;// (15)
9,12; // (16)
9,13; // (17)
10,14;// (18)
11,15;// (19)
12,16;// (20)
13,14;// (21)
14,15;// (22)
15,16;// (23)
13,16];//(24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0,-0.6,0,1,1,1; //node 1
0.75,-0.6,0,1,1,1; //node 2
0.75,0,0,1,1,1; //node 3
0,0,0,1,1,1; //node 4
0,-0.6,0.4,0,0,0; //node 5
0.75,-0.6,0.4,0,0,0; //node 6
0.75,0,0.4,0,0,0; //node 7
0,0,0.4,0,0,0; //node 8
0,-0.6,1.1,0,0,0; //node 9
0.75,-0.6,1.1,0,0,0; //node 10
0.75,0,1.1,0,0,0; //node 11
0,0,1.1,0,0,0; //node 12
0,-0.6,1.8,0,0,0; //node 13
0.75,-0.6,1.8,0,0,0; //node 14
0.75,0,1.8,0,0,0; //node 15
0,0,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_Tubes;
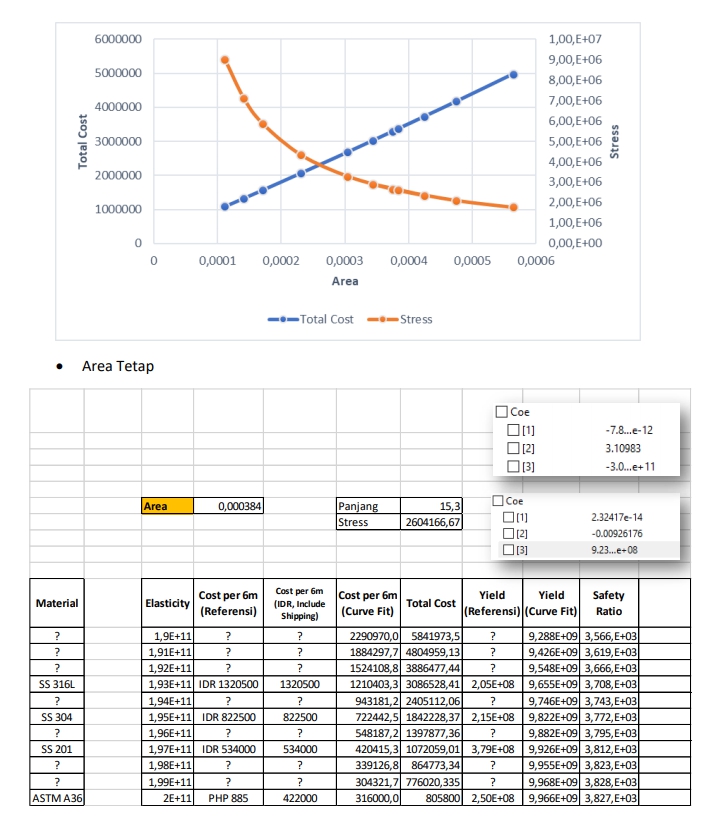
- Curve Fitting
Model
model callcurve
parameter Real [jumlah data] X={masukan nilai dari data};
parameter Real [jumlah data] Y={masuka nilai dari data};
Real [3] Coe;
algorithm
Coe:=Curve_Fitting(X,Y);
end callcurve;
Function
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
end Curve_Fitting;
Referensi Data
- https://www.theprojectestimate.com/angle-bar-price-list/
- https://mitarcahyaabadai.wordpress.com/2019/03/15/harga-besi-siku-stainless-steel-ss304-ss316l-2019/
- https://wijayamakmur.com/product/siku-ss201-50x50x4mm-x-6000mm/
- http://asm.matweb.com/search/SpecificMaterial.asp?bassnum=MQ316Q
- http://asm.matweb.com/search/SpecificMaterial.asp?bassnum=MQ304A
- http://www.matweb.com/search/datasheet.aspx?matguid=ebd318a706b845fda3939661849ed0a2
- http://www.matweb.com/search/datasheet.aspx?matguid=d1844977c5c8440cb9a3a967f8909c3a
- https://kilo.id/jasa-kirim-impor/philippines-indonesia