Dzalfa Rajaa' Muhammad
Contents
[hide]Pressurized Hydrogen Storage Optimization
Pressurized Hydrogen Storage
In pressurized hydrogen storage, hydrogen gas is compressed and stored in specially designed tanks or cylinders. These tanks are designed to withstand high pressures, typically in the hundreds to thousands of pounds per square inch (psi). Accumulators offer advantages such as simplicity, portability, and reduced refueling time. However, there are also challenges such as weight, security, and storage capacity limitations. Tank materials must be robust and require rigorous testing to prevent leaks and bursts. To overcome these limitations and optimize hydrogen storage and use, alternative storage methods such as cryogenic storage and hydrogen carriers are being explored.
Factors Involved in Designing and Optimizing a Pressurized Hydrogen Storage
Designing and optimizing a pressurized hydrogen storage involves several factors and processes to ensure its safety, efficiency, and performance. Here are some key considerations in the design and optimization process:
Storage Capacity The required storage capacity of hydrogen must be determined based on the anticipated demand and usage. Factors such as the desired duration of storage, refill frequency, and system requirements play a role in determining the storage capacity.
Material Selection The choice of materials for the storage tank is crucial. Factors such as material strength, corrosion resistance, hydrogen compatibility, weight, and cost need to be considered. The selected material should meet safety standards, regulatory requirements, and be suitable for the specific application.
Pressure Requirements Determining the optimal operating pressure is critical to balance storage capacity, tank weight, and safety. Higher pressures allow for more hydrogen storage within a given volume, but it increases material requirements and safety considerations. The pressure requirements should align with the intended use and regulatory standards.
Safety Considerations Safety is paramount in hydrogen storage design. Factors such as material integrity, leak prevention, pressure relief mechanisms, and appropriate safety measures need to be incorporated. Standards and guidelines from regulatory bodies, such as the International Organization for Standardization (ISO) and national safety codes, should be followed.
Structural Design The structural design of the storage tank must ensure its mechanical integrity and resistance to external loads, vibrations, and impacts. Finite element analysis (FEA) and other engineering calculations are performed to determine the optimal tank shape, thickness, reinforcement, and support structures.
Thermal Management Hydrogen storage systems may require thermal management to control temperature variations. Insulation, cooling, or heating mechanisms are employed to maintain the desired hydrogen temperature range and prevent thermal stresses.
Cost Optimization Optimization techniques, such as mathematical modeling and numerical methods, can be applied to minimize costs while meeting performance and safety requirements. This includes optimizing material usage, tank size, manufacturing processes, and other relevant parameters. Regulatory Compliance Compliance with relevant regulations, standards, and codes is essential in the design and operation of pressurized hydrogen storage. It ensures safety, environmental protection, and compatibility with industry norms.
Hydrogen Purity The required purity level of hydrogen for the specific application should be considered. Impurities in the hydrogen stream can impact the integrity and performance of the storage system. Depending on the application, purification processes may be needed to remove impurities.
Fill and Discharge Rates The desired fill and discharge rates of hydrogen affect the design and optimization of the storage system. Factors such as the available infrastructure, operational requirements, and efficiency considerations influence the sizing of valves, piping, and other components.
System Integration Pressurized hydrogen storage systems are often integrated with other components and subsystems, such as hydrogen production units, fuel cells, or transportation systems. Seamless integration and compatibility with these systems are important to ensure overall system performance.
Environmental Considerations Environmental factors, including temperature variations, exposure to corrosive substances, and seismic activity, should be taken into account during the design process. Adequate protection and design measures, such as coatings, seismic restraints, and environmental monitoring, may be required.
Manufacturing and Fabrication Methods The manufacturing and fabrication techniques employed impact the quality, cost, and scalability of the storage system. Selection of appropriate manufacturing methods, such as welding, forming, or composite layup, needs to be aligned with the chosen materials and desired characteristics.
Code
Storage system design and optimization occurs in several stages, from existing systems to meeting required limits. First, based on the required volume (1 liter), determine the plate size to use, taking into account the minimum plate area using the following calculation:
1. Import the math library and the minimize module from scipy.optimize.
2. Define the objective(x) function that takes x as an argument, which is an array containing the radius and height. This function calculates the surface area of a cylinder using the given formula.
3. Define the constraint(x) function that takes x as an argument, which is an array containing the radius and height. This function calculates the volume of the cylinder and ensures that it is equal to 1000.
4. Set the initial_guess for the radius and height.
5. Define the bounds for the radius and height. In this case, the radius and height must be non-negative.
6. Define the volume constraint (volume_constraint) as an equality (eq) constraint using the constraint function defined earlier.
7. Minimize the surface area of the cylinder by calling the minimize function with the objective function, initial_guess, 'SLSQP' method, bounds, and volume_constraint. Save the result in the result variable.
8. Retrieve the optimal values for the radius, height, and minimum surface area from the result object.
9. Print the results using the print statement, including the optimal radius, optimal height, and minimum surface area.
import math
from scipy.optimize import minimize
def objective(x):
radius, height = x
return 2 * math.pi * radius**2 + 2 * math.pi * radius * height
def constraint(x):
radius, height = x
return math.pi * radius**2 * height - 1000
initial_guess = [1, 10] # Initial guess for the radius and height
# Define the bounds for the radius and height
bounds = [(0, None), (0, None)]
# Define the volume constraint
volume_constraint = {'type': 'eq', 'fun': constraint}
# Minimize the surface area subject to the volume constraint
result = minimize(objective, initial_guess, method='SLSQP', bounds=bounds,
constraints=volume_constraint)
optimal_radius = result.x[0]
optimal_height = result.x[1]
min_surface_area = result.fun
print(f"\n\nOptimal Radius: {optimal_radius} cm")
print(f"Optimal Height: {optimal_height} cm")
print(f"Minimum Surface Area: {min_surface_area} cm²\n\n")
These calculations yield the following values:
● Optimal Radius: 5.419261255088046 cm
● Optimal Height: 10.838519182022262 cm
● Minimum Surface Area: 553.5810443894838 cm²
Furthermore, the calculation is performed with a given budget variable, ie Rp. 500,000. Use the following calculations for the calculations:
1. Import the `minimize` function from the `scipy.optimize` module.
2. Set the required `price_per_unit` and `capacity_per_unit` variables.
3. Set the maximum budget (`max_budget`).
4. Define the objective function (`objective_function`) that takes a variable `x` and returns the negative value of `x` multiplied by `capacity_per_unit`.
5. Define the budget constraint function (`budget_constraint`) that takes a variable `budget` and returns the difference between `max_budget` and the product of `price_per_unit` and `budget`.
6. Create the budget constraint equation (`budget_constraint_eq`) as an inequality constraint using the `ineq` type and the `budget_constraint` function.
7. Set the initial value (`x0`) to 0.
8. Define the bounds for the optimization problem as a list containing a tuple `(0, None)`.
9. Solve the optimization problem using the `minimize` function with the objective function, initial value, 'SLSQP' method, bounds, and constraints.
10. Store the solution in the `solution` variable.
11. Display the results using the `print` function, including the status of the optimization (whether an optimal cost is found or not), the number of units that can be purchased (`solution.x[0]`), the total storage capacity obtained, and the total budget required.
from scipy.optimize import minimize
# Required price and capacity price_per_unit = 500000 # Rupiah capacity_per_unit = 1 # Liter
# Maximum budget max_budget = 500000
# Objective function def objective_function(x): return -x * capacity_per_unit
# Budget constraint def budget_constraint(budget): return max_budget - (price_per_unit * budget)
budget_constraint_eq = {'type': 'ineq', 'fun': budget_constraint}
# Initial value x0 = 0
# Bounds bounds = [(0, None)]
# Solve the optimization problem solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=[budget_constraint_eq])
# Display the results
print("Status:", soluti.success and "Optimal Cost" or "No solution found")
print("Number of units that can be purchased:", solution.x[0])
print("Total storage capacity obtained:", solution.x[0] * capacity_per_unit, "liters")
print("Total budget:", solution.x[0] * price_per_unit, "Rupiah")
Here are the results I got:
● Status: Optimal Cost
● Number of units that can be purchased: 1
● Total storage capacity obtained: 1.0 liters
● Total budget: 500000.0 Rupiah
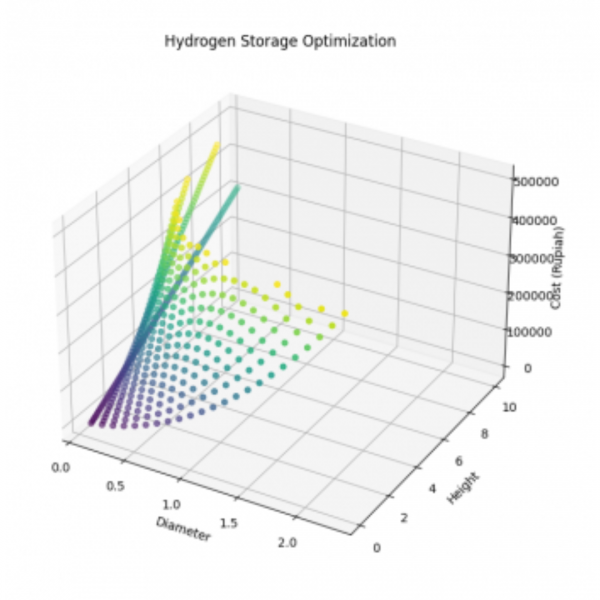
Using the above calculations, we can graph the capacity vs. quantity comparison obtained with the following code:
# Chart List unit_list = [] total_capacity_list = []
# Calculation of Optimal Solution for unit_count in range(int(max_budget / price_per_unit) + 1): total_capacity = unit_count * capacity_per_unit total_cost = unit_count * price_per_unit
if total_capacity > optimal_total_capacity and total_cost <= max_budget: optimal_unit_count = unit_count optimal_total_capacity = total_capacity optimal_total_cost = total_cost
# Adding data to the list for the chart unit_list.append(unit_count) total_capacity_list.append(total_capacity)
# Result Display
print("Number of hydrogen storage units to be purchased:", optimal_unit_count)
print("Total storage capacity:", optimal_total_capacity, "liters")
print("Total cost:", optimal_total_cost, "Rupiah")
# Displaying the Chart
plt.plot(unit_list, total_capacity_list, color='red')
plt.xlabel('Number of Hydrogen Storage')
plt.ylabel('Total Storage Capacity (liters)')
plt.title('Hydrogen Storage Optimization')
plt.grid(True)
plt.show()
The code used above aims to optimize hydrogen storage given the given capacity and budget constraints. The main goal is to determine the number of hydrogen storage units that should be purchased to achieve maximum storage capacity, taking into account the constraints used.
Iterations are performed to retrieve data for each unit purchased and capacity and other identified limits. We test each unit quantity to calculate total storage capacity and total associated costs. The iteration stops when the value exceeds the limit.