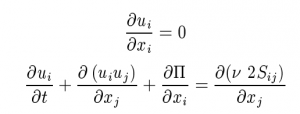Design and Analysis of Modified Tesla Valve Geometry Implementation in a Filter Chamber
Contents
Introduction
Power plants all around the world use various types of fuel such as fossil fuel, coal, and natural gas to generate heat for the system to work. Combustion in coal-based power plants in particular produces large amounts of particulate matter called as fly ash which can be hazardous towards the environment and human health. For this reason, filters are used in the system to remove said particulates from the gas before it is introduced to the environment.
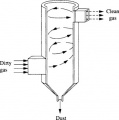
There are various types air controlling technologies which are implemented in power plants to improve the quality of gas released from the process. Common ones in the field are inertial seperators, fabric filters, scrubbers, and precipitators with each their own process, advantages and disadvantages.
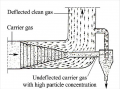
Inertial seperators in particular are devices that are used to filter particulates from the flow of gas going through the system by changing the direction of motion of the flow (Clift, 1997). The flow direction of motion is changed through use of various geometric designs such as baffles, cavities, cross section area changes, and so on. Through sudden introduction of these geometric designs, forces in the gas will concentrate the flow of particles to specific part of the gas flow which can be then seperated in chambers or other filtering surfaces. Once seperated, the particulates from the flow are moved to an outlet hopper or containter to be stored before disposed safely. Therefore, intricate design of these geometric structures inside the seperators play important role in increasing the overall efficiency of the filtering system. As most of this system doesnt require moving parts, they are at very low cost and maintenance as well.
Comparing other systems with intricate designs, the tesla valve is a fixed-geometry check valve which allows for one direction flow of fluid going through without use of any moving parts. As it allows unobstructed flow from one direction, various geometric structures inside the valve blocks the flow greatly by rearranging the flow to block one another hence resulting in great resistance. Other than its use as a check valve, the tesla valve has been implemented as well as micromixer to increase mixing performance by taking advantage of its geometry. In this case, it poses a question in whether there are other implementations for this geometry as it has similar concept to inertial seperators in rearranging fluid flow with its internal structures.
This research proposes the innovative idea of using a modified geometry of tesla valve in a particulate filtering system. The modified geometry is designed and simulated in aiming to find the feasibility of implementing similar tesla valve geometries and show how the efficiency in filtering can be affected in these systems.
Objective
For this research, the objectives are as following
- Design a geometry based on the tesla valve for gas-solid flow seperation purposes
- Simulate said geometric design through transient, subsonic, Incompressible, and LES configuration CFD simulation to mimic real life conditions
- Analyze the feasibility of tesla valve based geometry in filtering through parameters including (1) efficiency in filtering, (2) range of particle sizes effective to be filtered, (3) flow patterns, and (4) number of segments
- Verifying the result based on a grid independece study to ensure a small margin of error
- Validate results through various other similar studies
Methodology
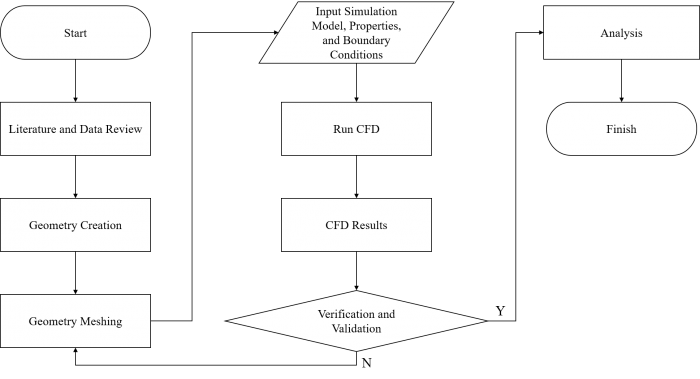
1. Outline of Process
The outline of this research are as the following.
2. Software Used
There are mainly 2 softwares used in this research which is to create the tesla valve geometry and to simulate the geometry in a CFD environment.
a. Geometry Modelling
For the geometry creation, the used software is Autodesk Inventor. Autodesk Inventor is a computer-aided design (CAD) software which provides professional-grade 3D mechanical design modelling with user friendly interfaces developed by Autodesk. Other than mechanical designing, inventor is also capable of structual simulation and documentation (drawing, animation, etc.).
b. CFD Simulation
The software used in the numerical CFD simulation especially pre-processing and solver is CFDSOF. CFDSOF is the first indonesian CFD software developed by PT CCIT Group Indonesia with a straightforward and easy to understand GUI. Geometry created from Inventor will be imported to CFDSOF to be meshed and processed numerically. Once done, the results are then analyzed with Paraview to observe various data such as flow field velocity, pressure, particulate distribution and etc.
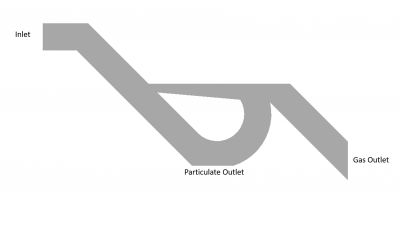
3. Tesla Valve Geometry
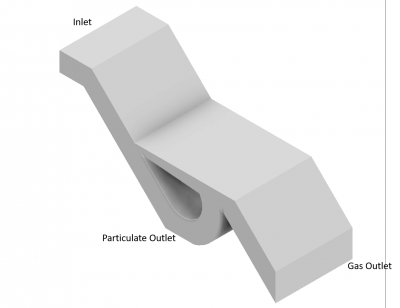
Below is the geometry designed for this research with Autodesk Inventor as the CAD software. The tesla valve geometry is slightly modified from the usual form to accomodate the purpose in filtering particulates from the flow of gas. The gas still mixed with fly ash would enter the geometry from the inlet which would be then flow through the structure trying to filter particulate before exiting through the outlet. The overall dimension of this geometry is set to be 90 cm x 32 cm x 46.3 cm
4. CFD Simulation Model
The simulation model set for this research are transient, incompressible flow, subsonic flow, Large Eddy Simulation (LES) turbulence, and multiphase Eulerian - Lagrangian model. The governing equation for this model are lised as below.
incompressible navier stokes equation for LES turbulence model (Frohlich & Rodi, 2002).
where
is the strain rate tensor and
5. Fluid Properties and Boundary Conditions
The properties for the fluid and solid phase are listed as below
| Properties | ||||
|---|---|---|---|---|
| Density (kg/m3) | Dynamic Viscosity (Pa.s) | Velocity Inlet (m/s) | Total mass (kg) | |
| Flue Ash | 1250 | - | 0,5 | 8 |
| Flue Gas | 0.9 | 2.14e-5 | 2 | - |
Results and Discussion
1. Meshing
a. Grid Indepedency Test
Grid Independency test is carried out to analyze the effect of mesh size on simulation results. This test is done to ensure minimum error in the simulation as well by ensuring the results do not deviate too much over changes in mesh size used in the test. The test is done in 5 mesh configurations and comparing the velocity at a point in the outlet plane as shown below.
| Grid Indepedency Test | ||||
|---|---|---|---|---|
| No | Grid Division | V @ Outlet | ||
| x | y | z | ||
| 1 | 30 | 30 | 20 | 1.74 |
| 2 | 40 | 40 | 30 | 2 |
| 3 | 50 | 50 | 40 | 1.64 |
| 4 | 60 | 60 | 50 | 1.07 |
| 5 | 70 | 70 | 60 | 0.94 |
As shown by the results above, the velocity from the 5th configuration with highest grid division deviate by a very small margin from the 4th configuration. Therefore, this configuration is stable with minimal error to be used in the entire research.
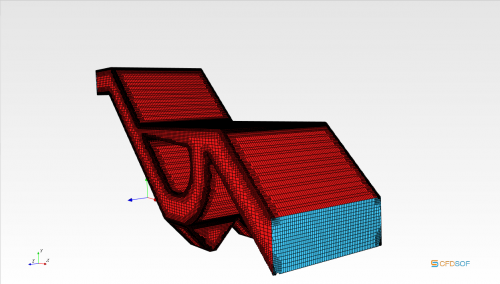
b. Final Meshing Result
As discussed before, the mesh configuration used is 70 x 70 x 60 with maximum value of 2 for surface refinement. Boundary configurations on the geometry are as inlet flow from the obstructing side of the geometry and outlet on the non-obstructing side.
c. Residual Value
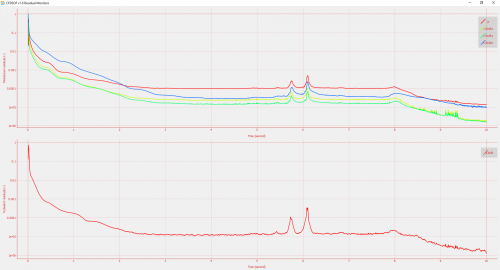
With the simulation running in Transient, LES, Incompressible, Subsonic, and Multiphase Lagrangian - Eularian configuration, the precision control on the simulation is made to approach value of 10^-6. The residual value below shows convergence starting from 2 second of the simulation. The simulation experiences slight unstabiliy around 7 second before returning to convergence and reaching value of 10^-6 about 8 seconds in.
2. Results
a. Pressure Distribution
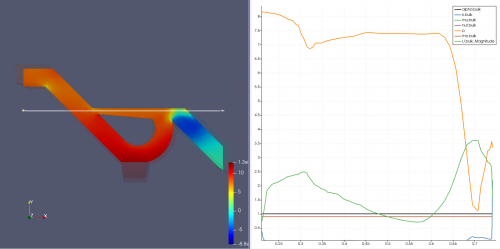
As shown by the image below, the pressure inside the geometry is initially very high till the end of the tesla valve segment. This result stands with how the tesla valve is designed to restrict fluid flow from the obstructing end (Nikola, 1920). Moving past the valvular segment, the flow inside experiences drop in pressure as there are no longer any obstructing geometry for the flow.
b. Velocity Distribution
As shown in the pressure distribution before, the obstructed flow from the valvular geometry causes low velocity from entry to the end of the tesla segment. From then on, the flow experiences large increase in velocity.
c. Geometry Effect on Particle Filtering
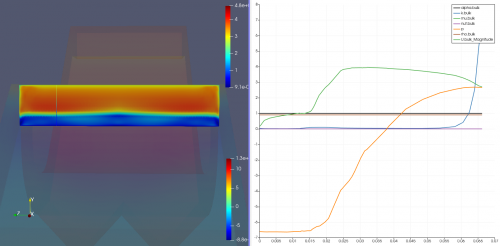
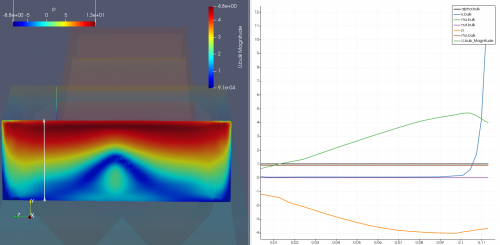
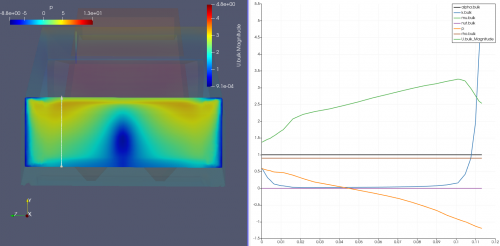
As initially proposed, the effect of the tesla valve geometry on particulate filtering is simulated. There are two cases which can be discussed from the flow of the particles, first is the flow above through the smaller area and the second is the flow below through the larger area and curve. For the first case, particles flowing through this region is not entirely filtered as some flow right through the geometry while some settles and sticks to the inner plane. for the second case, most of the particles flowing through the region below is held back by the curve in the geometry which causes the particles to fall back to the hopper below.
While trying to get the data on efficiency of filtering from the total mass and size of particles exiting, the writer is unable to find the precise results as paraview experiences crashing upon calcution. By the image shown below, the geometry is able to filter large particulates from the range of 4x10^-5 m to 1x10^-4 m while smaller particles are still able to get through. This problem can be solved by adding more tesla valve segments to increase efficiency in filtering although further research are required to confirm.
Conclusion
The tesla valve geometry was proposed and designed to be implemented in a particulate filter chamber. Simulation results show fluid flow as how it would react in an actual tesla valve geometry obstructed. the effectivity to filter particulates are still unknown due to paraview crashing and unable to extract the exact mass and size range of particles escaping the geometry. to some extent, the geomtry is still able to filter particles as shown in the results although some are able to flow through. This can be mended with implementing more valvular segments on the geometry to ensure maximum filtering of particles.
References
Clift, R. (1997). Inertial separators: basic principles. In Gas Cleaning in Demanding Applications (pp. 41-52). Springer, Dordrecht.
Fröhlich, J., & Rodi, W. (2002). Introduction to large eddy simulation of turbulent flows.
Nikola, T. (1920). U.S. Patent No. 1,329,559. Washington, DC: U.S. Patent and Trademark Office.