Chandra Pratama Rinaldi
Contents
- 1 Pertemuan Pertama Metode Numerik 06/02/2019
- 2 Tugas Metode Numerik 2
- 3 Pertemuan 3 Metode Numerik 20/02/2019
- 4 Tugas 3 Latihan Eliminasi Gauss
- 5 Tugas 4 Membuat Break Even Point
- 6 Rangkuman Metode Numerik 06/03/2019
- 7 Tugas Pegas Metode Numerik
- 8 Flowchart Pegas
- 9 Tugas Defleksi Beam
- 10 UAS Metode Numerik: Algoritma Root Finding
Pertemuan Pertama Metode Numerik 06/02/2019
Tujuan Perkuliahan Metode Numerik adalah memahami konsep/prinsip dan mampu menerapkannya. Selama ini kita belajar di sekolah, saya hanya membaca melalui satu/dua buku saja. Terlebih, pada pelajaran Matematika, saya hanya mengetahui rumus untuk menyelesaikan suatu masalah, bukan memahami mengapa kita harus menggunakan rumus tersebut. Ketika memasuki kuliah, saya baru mengerti asal mula rumus tersebut dikonsepkan. Dalam mata kuliah Metode Numerik, akan lebih banyak belajar tentang pemrograman dasar, seperti algoritma, flowchart, metode iterative, penyelesaian persamaan-persamaan aljabar simultan, diferensial dan integral, optimasi, serta studi kasus.
Pemrograman pada masa kini sangat penting karena banyak persoalan yang tidak bisa diselesaikan dengan metode menghitung secara manual. Contohnya dalam membuat analisis tegangan balok (beam) serta metode finite element analysis yang dapat mengetahui distribusi beban. Kemudian, pemrograman dapat membantu mendesain suatu benda menjadi lebih mudah seperti adanya program Matlab, Autodesk Inventor, dan lain sebagainya.
Dalam hakikatnya, manusia senantiasa harus mengenal siapa dirinya sendiri, karena manusia diberikan kemampuan untuk berpikir dan mempunyai akal. Dalam mengenal diri sendiri, manusia akan terus belajar, memperbaiki kesalahan dan menjadi lebih baik di masa depan kelak.
Diskusi dan Tugas Metode Numerik
Tugas Metode Numerik 2
Tugas Metode Numerik 2
Untuk membuat persamaan seperti "Ax + By = C" dan "Px + Qy = R", maka dapat menggunakan program pengkodingan Python dengan menuliskan persamaan tersebut sebagai matriks, dengan cara sebagai berikut:
import numpy as np
A = np.array([
[a, b, c] ])
B = np.array([
[p, q, r] ])
print A + B
print A - B
Pertemuan 3 Metode Numerik 20/02/2019
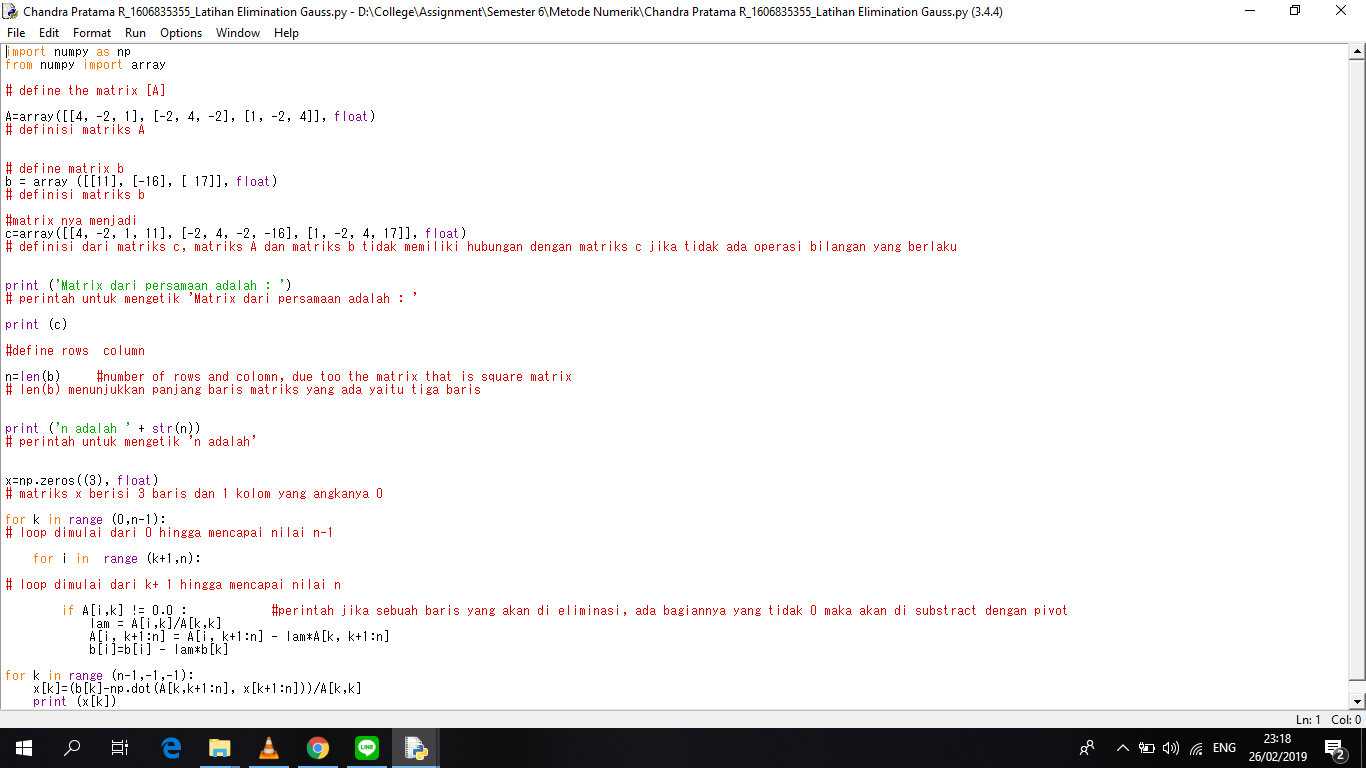
Operasi hitung dengan Python mirip penjumlahan deret. Namun, Python hanya mampu melakukan operasi bilangan dasar (penjumlahan, pengurangan, perkalian, pembagian). Operasi Python menggunakan metode eliminasi Gauss dengan menetapkan satu pivot baris dan kolom sehingga matriks tersebut membentuk matriks segitiga bawah.
Notasi dalam baris Python adalah sebagai berikut:
n = jumlah baris/kolom
i = baris ke
j = kolom
k = pivot
Pengkodingan eliminasi Gauss seperti yang tercantum dalam Bab I adalah sebagai berikut:
from numpy import dot
def gaussElimin(a,b):
n = len(b)
for k in range(0,n-1):
for i in range(k+1,n):
if a[i,k] != 0.0:
lam = a [i,k]/a[k,k]
a[i,k+1:n] = a[i,k+1:n] - lam*a[k,k+1:n]
b[i] = b[i] - lam*b[k]
for k in range(n-1,-1,-1):
b[k] = (b[k] - dot(a[k,k+1:n],b[k+1:n]))/a[k,k]
return b
Tugas 3 Latihan Eliminasi Gauss
Tugas 4 Membuat Break Even Point
Cara membuat BEP disini https://www.youtube.com/watch?v=OamGR_LwZDU&feature=youtu.be
Hasil BEP dapat diakses di https://www.youtube.com/watch?v=UUhLhIaesMA&feature=youtu.be
Rangkuman Metode Numerik 06/03/2019
Regangan merupakan laju perubahan panjang PR menghitung tentang analisa struktur sederhana
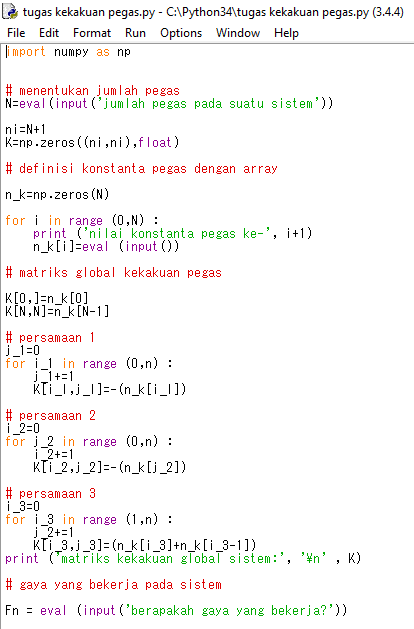
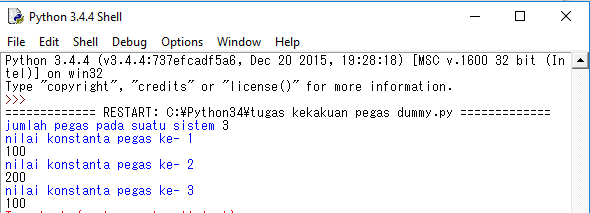
Tugas Pegas Metode Numerik
Flowchart Pegas
Tugas Defleksi Beam
Dapat diakses disini: https://youtu.be/dMDgmpFigGU
UAS Metode Numerik: Algoritma Root Finding
Dapat diakses disini:
https://www.youtube.com/watch?v=zc139vz-59E&t=19s
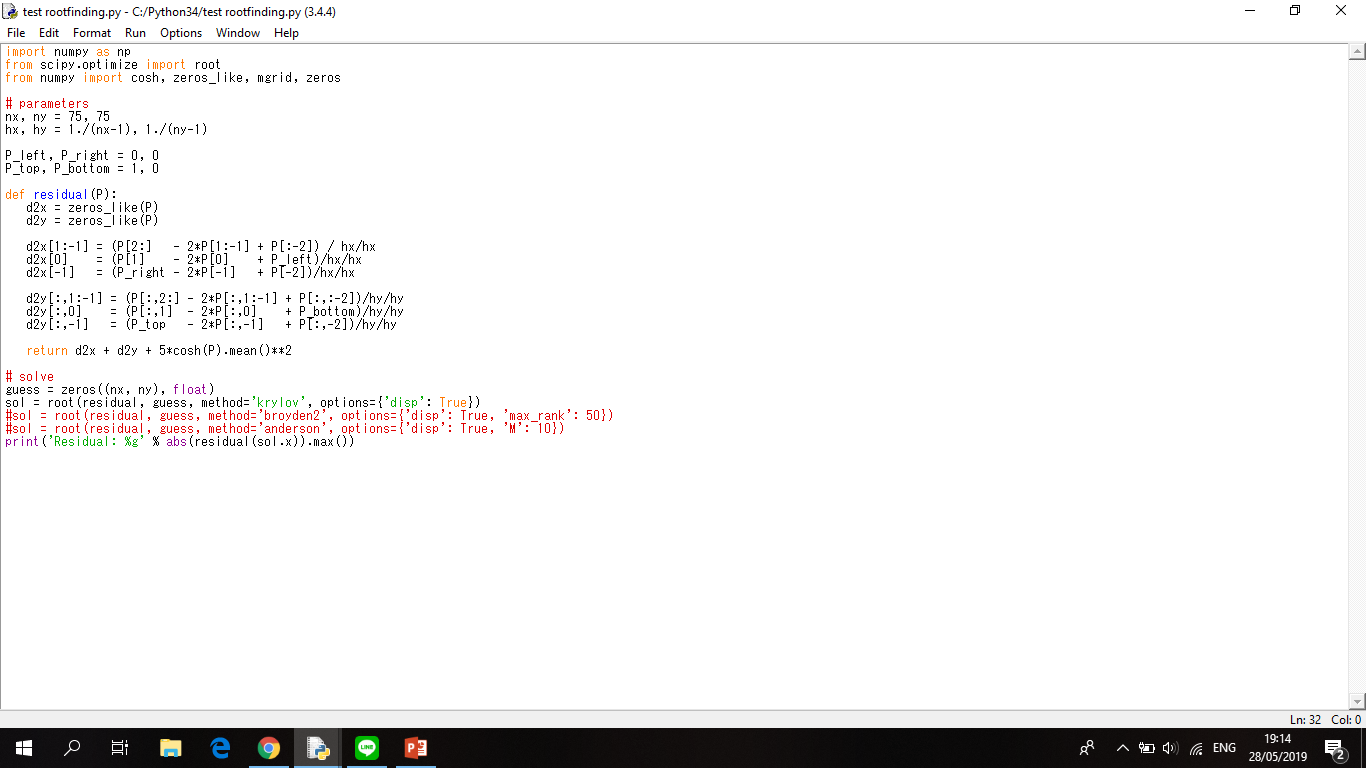
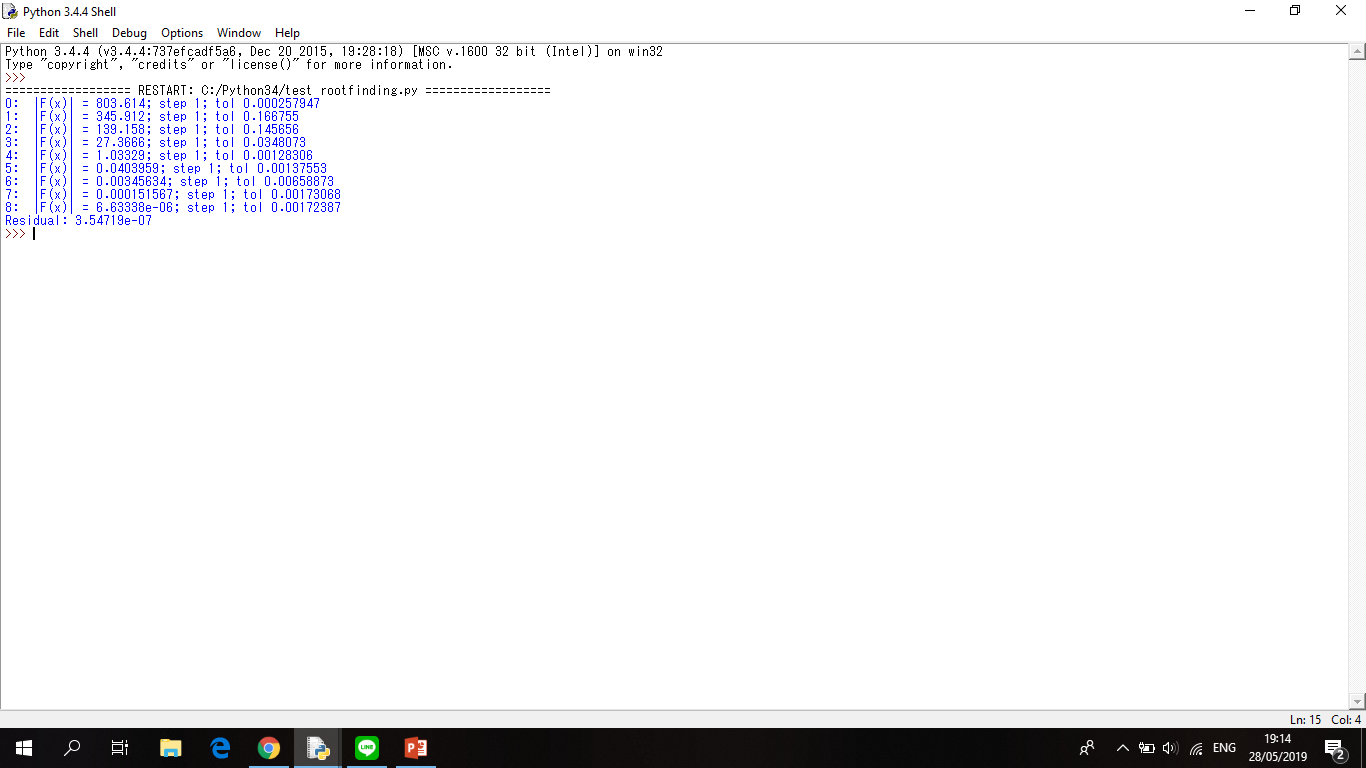
Link Python: https://drive.google.com/file/d/14VJqEVHpngC7gY07ghllBi_DpQ5aK4RX/view?usp=sharing
Link PowerPoint: https://drive.google.com/file/d/1jEQ5ZvbdaB6iPSZ5NkhkWVLF1B3O7tR_/view?usp=sharing