Benarido Amri
Contents
[hide]- 1 Introduction
- 2 Numerical Method
- 3 Energy Conversion System
- 3.1 Class Summary (Monday, 30 October 2023)
- 3.2 Vertical Axis Wind Turbine (VAWT) CFD Simulation Using CFDSOF
- 3.3 CFD Simulation Software
- 3.4 Class Summary (Wednesday, 8 November 2023)
- 3.5 Static 2-Dimensional Simulation of a Single Blade
- 3.6 Revised Static 2-Dimensional Single Blade Simulation
- 3.7 Axial Fan and Compressor Basic Principles
- 3.8 Force Comparison Result of Manual Calculation and Simulation
- 3.9 Turbomachinery
- 3.10 Pneumatic and Hydraulic
- 3.11 Steam Turbine
Introduction
- Full Name : Benarido Amri
- NPM : 2106718230
- Major : Mechanical Engineering
- Email : benarido.amri@ui.ac.id
- Lecturer : Dr. Ahmad Indra Siswantara
Assalamualaikum Wr. Wb.
My name is Benarido Amri currently studying Mechanical Engineering at Universitas Indonesia. this page would be a way for me to update the progress of learning Numerical Method and Energy Conversion System.
Numerical Method
Design Project
Pressurized Hydrogen Storage
Hydrogen can be a great alternative for conventional electric vehicle energy source, since it can provide many benefits such as less charge time and cleaner environmental waste. However, the problem we face with hydrogen is the safety concerns regarding its storage method, even though hydrogen is generally safe under normal pressure, it can be a major safety issue when stored at such a high pressure -which is how the hydrogen will be stored in a EVs-, upon accident many worried that the hydrogen could explode, or catch fire.
In this Numerical Method class, our ultimate goal would be to find a way to safely contain pressurized hydrogen. Although we are going to focus on a much smaller case and less pressure. With the specifications being 1 liter of hydrogen pressurized to 8 bar.
Hydrogen Application
Hydrogen is the lightest element in the universe and it can be used for many applications. There are many forms of hydrogen such as liquid form, gaseous form, and even solid form. These form have different uses of their own. Here are some applications for hydrogen according to their various forms:
- Liquid form hydrogen = Liquid form hydrogens are commonly used as a fuel for rocket, where it is used alongside an oxidizer. Apart from rocket fuel, liquid hydrogen can also be used as a fuel for internal combustion engine (ICE) and fuel cell.
- Gaseous form hydrogen = This form of hydrogen can potentially be a great alternative fuel source for vehicles such as cars or trucks.
- Solid for Hydrogen = There is currently a research on the possibility of storing hydrogen as a solid for vehicle fuel.
Optimization Consideration
We were tasked of designing a pressurized hydrogen storage tank which can hold up to 1 liter of 8 bar hydrogen which costs less than Rp. 500 000. For the optimization, we wanted to optimize the cost without sacrificing the performance such as safety, and reliability.
Material Selection
The current material selection for the storage is generally made of metal such as austenitic stainless steel (AISI 316 and AISI 304). This is because hydrogen storage must have very high tensile strength, low density, and doesn't react with hydrogen.
Optimization Objective
- Design Variables = Thickness, weight, and deflection.
- Objective Function = To find the most suitable wall thickness when considering the trade off between weight and strength (deflection) of the storage tank.
- Constraints = The storage tank must be able to fit within a space of 5.8325 cm x 5.8325 cm x 11.0234 cm rectangular box shape or around 1.5 L of volume. And must be able to hold a minimum of 1 L of hydrogen.
For the storage tank project, I will attempt to optimize the wall thickness of the tank by considering the weight and deflection. Weight can be a crucial factor especially when the storage tank is for applications that needs to be mobile and light. However if we were to use the same material, reducing weight can have an effect on its strength, one aspect of strength compromised is its ability to resist deflection when given a force.
The optimization process is done by using a graph to find the intersection point between deflection and weight. Due to the many formulas and equations involved, we can simplify the calculation by using a code such as python or MATLAB. In my case, I will be using a python programming language.
Design
Before we can calculate the weight and deflection, we need to define our material, shape, and also size. The shape of the tank can be divided into 2 basic geometry, the main cylinder and the cap on both sides. The total dimension of the storage tank is 11.0234 cm in length and has a radius of 5.8325 cm. The main cylinder has a height of 5.1909 cm and a radius of 5.8325 cm, while the cap has a radius of 5.8325, a height of 2.91625 cm, and a fillet radius equal to half of the main cylinder radius. These description can be seen on the image below.
The size and shape is taken from Jiddan's work on the ideal radius to height ratio of such storage tank, determining the ideal ratio to be around 1.89.
For the material, from the paper "Materials for hydrogen storage" by Andreas Zuttel, they stated that the common material for hydrogen storage is stainless steel AISI 316 and AISI 304, which is an austenitic type steel. So for the design project I decide to use the stainless steel AISI 304. AISI 304 is quite a common material and it is often used for many applications outside of the storage tank.
Coding
Due to the many variables and formulas involved, coding can be a great tool to help us calculate all the numbers for the graph. The code starts with importing the necessary modules from the library. The next step would be to define the known parameters, in this case the total height, outer radius, cylinder height, total volume, modulus of elasticity, and the simulated force.
We use the the same for loop to calculate all the necessary variables, such as the weight and deflection. Here we have the equations used to calculate the variables shown in figure 2.2.
To calculate the deflection, only the main cylinder is calculated with the assumption of the load situated at the middle of the cylinder. This is to simulate an impact at the center of the tank while the tank is empty and thus there is no pressure acting on the inside of the cylinder. This assumption may not be accurate, however since I couldn't find the appropriate formula for the shape of the whole storage tank, we will need to go by this assumption. The diagram of the calculation can be seen in figure 2.3.
h_t = 11.0234 # Total height
r_o = 5.8325 # Outer radius
h = h_t - r_o # Cylinder height
V_t = 1454.8338 # Total volume
E = 193e9 # Modulus of elasticity for AISI 304
F = 100000 # Simulated force
results1 = []
results2 = []
results3 = []
for r_i in np.arange(5, r_o - 0.0025, 0.0025):
fluid_volume = ((4*(r_i**2)) * h_t) - (pi * (r_i**2) * (4/3 * 1/64 * r_i + 1/16 * h))
material_volume = V_t - fluid_volume
weight = material_volume * 8 # Weight is the volume times the density of material (8 gr/cm^3)
thickness = (r_o - r_i)/2 * 10 # Calculating the thickness in (mm)
deflection = ((F * (h_t/100)**3)/(48 * E * (pi/64 * (((2 * r_o/100)**4)-((2 * r_i/100)**4))))) * 1000 # Calculation of the deflection converted to (mm)
results1.append(weight)
results2.append(deflection)
results3.append(thickness)
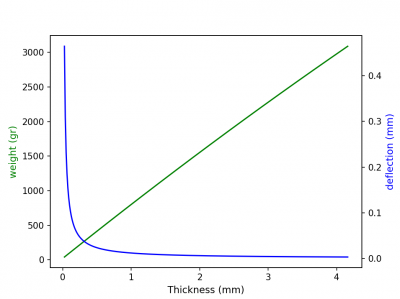
From the code above we can then plot the values into a graph as shown below :
From the graph by finding the intersection between the two lines, we can find the best wall thickness, which is around 0.312 mm. With a weight of 266.7 gram and a deflection value of 0.03775 mm.
Conclusion and Evaluation
Based on the result above, the ideal thickness when considering only the weight and the deflection factor would be 0.312 mm, however we must also consider other factors when designing or manufacturing storage tank. Although the result of the wall thickness seems to be very thin, this is probably due to the assumptions of taking only the wall cylinder.
We can change the wall thickness according to different materials and their properties, a stronger material would reduce the thickness even more whilst weaker material requires thicker wall.
Other interesting note that we can take from this procedure is that it is relatively simple to do, and can be done for many other parameters that we wanted to know, the accuracy however may not be as accurate as some other methods.
For further improvements, I think the best approach is to make the calculations more detail and more realistic, it will also be a great addition if we include simulation such as from ansys, solidworks, or other CAD software. There are some assumptions that might not be ideal for the optimization and also there are some idealization that might not be suitable for this particular case.
As mentioned previously, this approach only accounts for the weight and deflection and not other important factors. Since we are focusing on the optimization aspect of the design process, I only took certain parameters to work on while ignoring other crucial factors. Upon designing and manufacturing a product, we must consider all the factors and must also design according to the code, from its dimensions, safety, reliability, cost, and others.
Conscious Effort
Consciousness is an integral part of our lives, it allows us to have the ability to think, make decisions, and also differentiate between right and wrong. When we are working on this project, there are a lot of decisions and calculations that we have to make, such as at the start where we decide what variable(s) we want to optimize or towards the middle where we think about the code or at the end where we arrive at the conclusion of our project.
All of these different things that we did require a conscious effort, thus it is important for us to recognize and cherish our consciousness. And lastly, we have to be grateful for the opportunity that is given to us to experience our life, and have our own consciousness.
Final Presentation Video
My presentation video about my conscious effort on learning numerical method and its application in hydrogen storage design optimization can be found on the link below:
https://www.youtube.com/watch?v=EdskKzZS2bE
In this class, I have learned a lot about the importance of recognizing my own consciousness "I am my own consciousness" and how significant of a role it plays in our every day lives, from the second we woke up from sleep in the morning to the second we sleep again at night. Consciousness grants us the ability to do things that are integral to our lives, such as deciding between right and wrong, or having the ability to solve complex problems, or the ability to decide between several choices, or the ability learn new things and have many different perspective, and many others.
However, even though consciousness is important in our lives, we sometimes forget how essential it is for our lives, therefore it is important for us to recognize and appreciate our own consciousness and also be grateful of it.
Energy Conversion System
Class Summary (Monday, 30 October 2023)
“Education is what remains after one has forgotten what one has learned in school.”
- Albert Einstein
There are 3 levels of understanding in general, the first level is to first understand the “what”, the second level is about the “how” and lastly is to understand the “why”.
If we apply the 3 levels above to energy, we can answer the “what” question in terms of equation shown below:
dE/dt=W+Q
One of the fundamentals of energy is that it can neither be destroyed nor created, instead, it can only be converted. In practical fluid system application, energy conversion is present in pumps or turbines. To maximize the conversion, we need to understand the importance of efficiency. Efficiency in pumps are the measure of the ratio between the energy at output and at input.
Vertical Axis Wind Turbine (VAWT) CFD Simulation Using CFDSOF
Set Parameter Values
- Start time = 0
- End time = 2
- Inlet velocity = (12 5 0), 12 at the x-axis and 5 at the y-axis
Results
Pressure results
- Pressure Magnitude
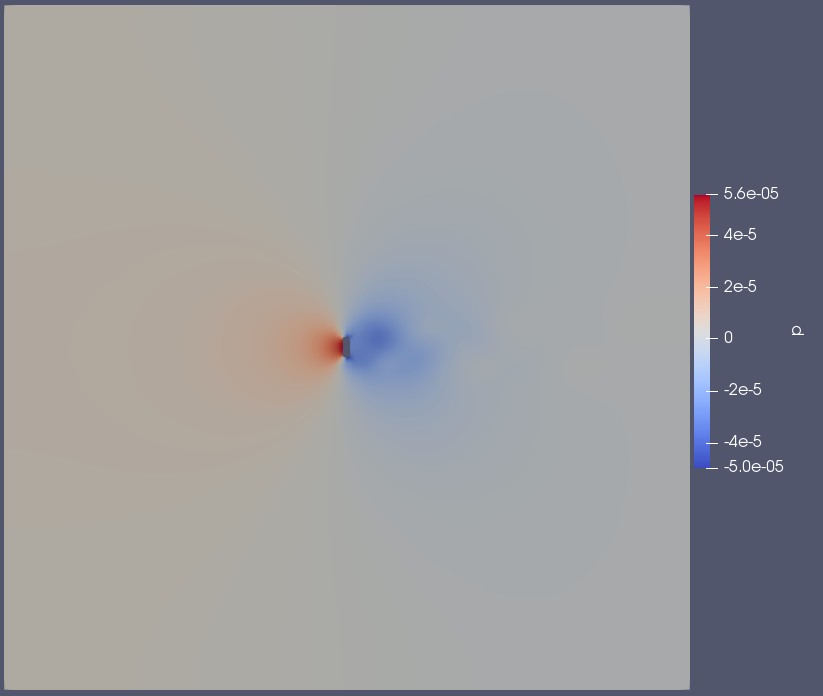
The result of the pressure magnitude is presented in figure 3.1.
- Pressure at t = 0.045
A clear pattern can be seen on figure 3.1 where the difference in pressure is indicated by the colors, where blue indicates lower pressures and the red color indicates higher pressure regions. At the turbine area, a low pressure region can be observed on the near side (relative to the axis of rotation) of the bottom airfoil, and a higher pressure region on the far side (relative to the axis of rotation) of the bottom airfoil.
However, there is a slight abnormality that can be seen at the top middle of the figure 3.2, a lower pressure region which does not seem to be interacting with the simulated object (VAWT).
- Pressure at t = 0.87
At t = 0.87, a similar situation can be observed in the simulation, where there is a clear difference in pressure between the far side and near side of the airfoil.
- Pressure at t = 1.045
A clear difference in pressure is observable, however, in this instance, the higher pressure region is present at the near side of the top right airfoil as opposed to the far side which was the case for the previous 2 timeframe. Furthermore, the most observable pressure difference seems to be when the airfoil is almost at a perpendicular angle to the direction of the wind.
Velocity Results
- Velocity Magnitude
The result of the velocity magnitude is presented in figure 3.1.
- Velocity at t = 0.045
The pattern for velocity changes is much more observable and clearer when compared to the pressure simulation. The color indicators are the same however, where blue indicates lower velocity and red indicates higher velocity. Although the patterns are more observable, it is more difficult to draw a correlation from the result of the simulation.
But there are still some pattern that are observable, such as the velocity profile is relatively turbulent, especially at the longer distances from the airfoils.
Another abnormality is also present in the velocity simulation similar to the previous simulation. It is also at the same exact location as the previous one.
- Velocity at t = 0.87
The turbulent nature of the velocity pattern is much more observable at t = 0.87. Especially at the two bottom airfoils of figure 3.7.
- Velocity at t = 1.045
Similar to the previous timeframe, a turbulent pattern is observable for all airfoils.
Difficulties
Although the intention was to set the end time to 2, due to the high processing power requirement, I was only able to get the time to 1.135.
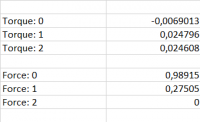
Torque & Force Result
The torque and force results are presented in the figure 3.9.
CFD Simulation Software
In the past, it is often difficult to test a design since we need to have the appropriate testing equipment and then create a prototype from the design. And then, calculations of non-dimensional number such as Reynolds number is required in order to have accurate testing. Furthermore, it is often difficult to decipher all the information based on the testing result.
In the digital age, an alternative method of design testing is available. With the help of simulation software such as CFDSOF, Ansys, SimFlow, Autodesk CFD, and others, testing can be done with relatively minimum effort with much more detailed results. By using simulation software, details such as pressure or velocity at each points on the model can easily be viewed.
Simulation software allows for more efficient and cost effective way to optimize or test a design.
Class Summary (Wednesday, 8 November 2023)
To learn about the simulation, a simplified version of a turbine is used whereby the turbine only has 2 blades. This simplification is in order to learn the basics of the CFDSOF software. It also enables us to understand how the energy is converted following a basic formula of kinetic energy, potential energy, pressure, and velocity.
Static 2-Dimensional Simulation of a Single Blade
Parameters
- Box geometry properties: 1 m X 3 m X 1 m
- Base mesh: 10 m X 10 m X 0.1 m
- Velocity reference value: 0.01 m/s
- Simulation mode: Steady-state, laminar, incompressible
- Initial condition = Fixed value velocity with 0 m/s speed
Result
Pressure
From the figure above, a high pressure region is visible at the front side of the blade. These higher pressure region can be one of the causes of the turbine to ultimately rotate on its axis of rotation. Theoretically, the larger the surface area of the blade, the more pressure will develop at the front of the blade. However, larger surface area also means more material is needed thus adding weight as well.
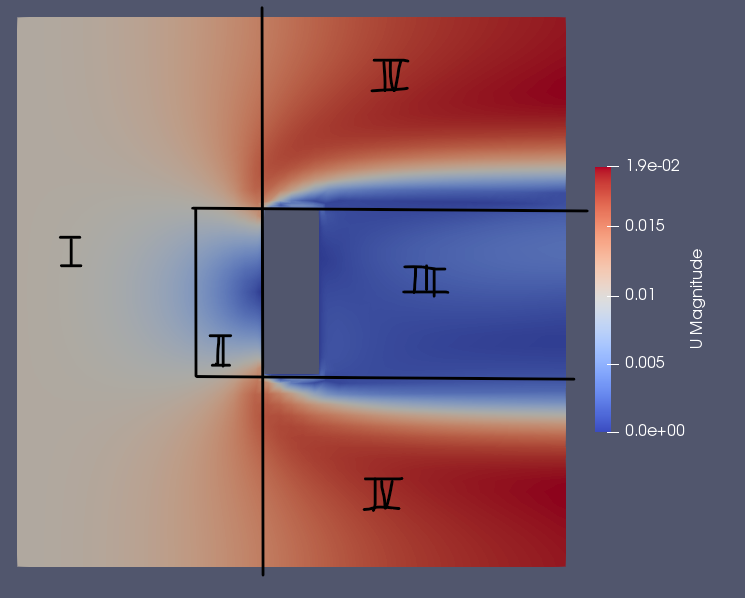
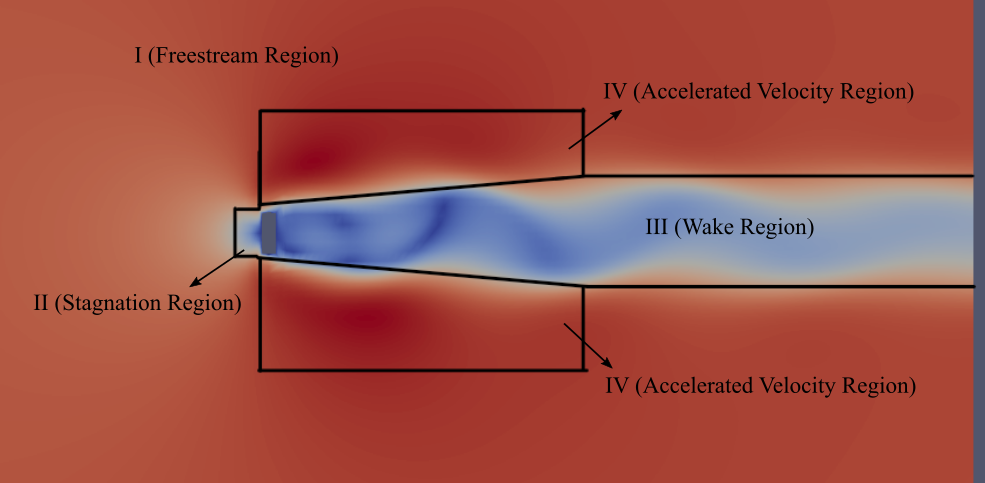
Several interesting points can be drawn from the figure above:
- The left input side is relatively uniform. (Area 1)
- A small area right in front of the blade has 0 velocity. (Area 2)
- The area covered by the blade has relatively low velocity. (Area 3)
- However, the area above and below has a highest velocity amongst the other areas. (Area 4)
The increase in velocity in area 4 can be explained simply as the fluids way of maintaining the same flow rate throughout the control volume. The equation is Q1 = Q2 or V1 * A1 = V2 * A2, because of the obstruction caused by the blade, the area of the control volume decreases, thus to maintain the same output flowrate, the velocity of the air must increase as well. Creating the shape and pattern as seen in the figure above.
Revised Static 2-Dimensional Single Blade Simulation
Parameters
- Box geometry properties: 0.1 m X 0.3 m X 1 m
- Base mesh: 10 m X 10 m X 0.1 m at 200 X 200 X 1 division
- Velocity reference value: 0.01 m/s
- Simulation mode: Steady-state, laminar, incompressible
- Initial condition = Fixed value velocity with 0 m/s speed
Result
Pressure
Velocity
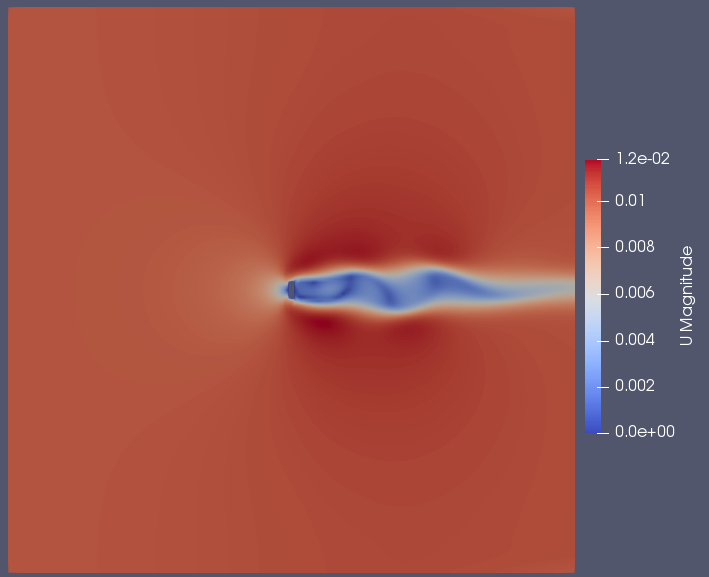
Due to the much larger ratio between the control volume and blade size, a clear freestream region is visible outside of a certain radius of the blade.
As seen on the zoomed velocity simulation figure above, the result of the simulation is relatively similar to the previous case. However a clear fluid turbulence is visible on the third (wake) region.
Axial Fan and Compressor Basic Principles
Video link: https://www.youtube.com/watch?v=uv6Keiw0H94
Overview
An axial fan or compressor is a device that transfer or compress fluid which travels in parallel with the axis of rotation of the blade.
A few characteristics of axial fan and compressor:
- Usually used for low pressure application
- Effective in higher flow rates
- Have a relatively high efficiency
Axial Fan
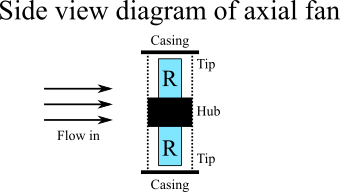
An axial fan can be simplified to only 3 main parts:
- Casing = Depending on the model, some casing encapsulate the fan all around whilst others leave the front and rear open (With the front and rear guard are shaped in such a way to still provide inlet and outlet flow). A casing is used to protect the blade or user from coming in contact with the fast rotating blade. Additionally, the casing also provide a way for the other components to be mounted.
- Hub = A hub in an axial fan serves as to provide a mounting point for the blades. Furthermore, many axial type fans house the motor within the hub.
- Blade/rotor = The blade in an axial fan can have a multitude of different shapes and size. It allows the fan to move the air from its inlet to its outlet.
Axial fans have multiple application in the industrial and in regular consumer, such as house fan, computer fan, AC units, and in industry such as in large ducting, HVAC systems.
On some cases, axial fan can also be equipped with a guide vane to help inflow.
 Image downloaded from realsimple.com
Image downloaded from realsimple.com
 Image downloaded from pinterest.co.uk
Image downloaded from pinterest.co.uk
Energy conversion
Electrical energy >>> Rotational energy (of shaft) >>> Fluid energy
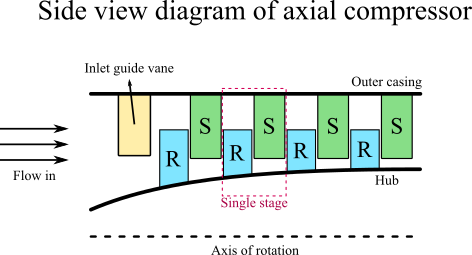
Axial Compressor
Axial compressors are more difficult to understand since they have much more parts, rotor, stator, guide vane, casing, and hub.
- Flow comes in from the left side of the figure.
- The inlet guide vanes help direct the flow towards the first rotor (which begins the first stage).
- The fluid then exits the rotor and enters the stator.
- The exiting of fluid through the first stator completes the first state.
- The cycle then repeats again through the stages.
- The number of cycles will depend on the design of the compressor.
These stages will change the properties of the fluid, with different pressure, temperature, and velocity in each stage.
A few notes:
- A combination of rotor and stator is called as "stage".
- Axial compressors are typically found as a part of jet engines.
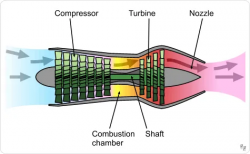 (Image downloaded from wikipedia.org)
(Image downloaded from wikipedia.org)
Force Comparison Result of Manual Calculation and Simulation
Assumptions
- Steady-state, laminar, incompressible
- Area of (0.3 * 0.1)m
- Air density of 1.225 kg/m^3
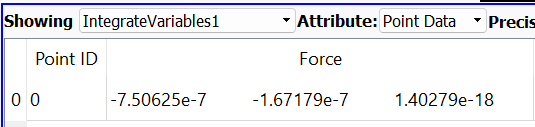
Simulation
From the simulation, the result of the force on a single blade is -7.50625e-7 in the x-axis.
Manual Calculation
From the manual equation, by utilizing the momentum change (shown in the figure above), with the assumption of velocity 2 of 0.012 m/s and velocity 1 of 0.01 m/s and with the flow rate velocity using velocity 1.
The manual calculation yielded a result force of 7.35e-7 N.
Analysis
- Fx(sim) = -7.50625e-7 N
- Fx(Calc) = 7.35e-7 N
Both manual calculation and simulation produced a relatively similar result, however for the manual calculation the result is positive where as the simulation, the force is negative. The difference in the signs are perhaps due to the different assumptions when calculating the force, since in the manual calculation, the force is on the wind hitting the blade, and the simulation is vise versa.
It is also important to recognize that we as human have consciousness, something which a computer can not have.
Turbomachinery
Turbomachinery is a rotational machine that interacts with the fluid. A turbomachinery can be divided into two categories: A machine that absorb power to increase the fluid's pressure or head such as pump, fan, compressor, blower or a machine that produce power by lowering the fluid's pressure or head such as wind turbine, gas turbine, water turbine. The second category of turbomachinery can be further divided based on how they utilize pressure or kinetic energy: A reaction turbine is a machine that utilize a change in pressure, whilst an impulse turbine utilize the kinetic energy (usually by increasing the velocity of the fluid through a nozzle). One example of a machine that utilize both turbine and compressor is a turbocharger.
Questions and Answers
- What is a turbocharger?
- When can a turbocharger run?
- Why is a turbocharger used?
- Where can I find a turbocharger?
- How does turbocharger work?
- How does turbocharger receive its power?
A turbocharger (which can be found in cars, excavators, or other machines) is a device that is used to compress air before entering the Internal Combustion Engine (ICE) resulting in more power from each engine stroke. A turbocharger's performance is highly dependent on the amount of exhaust gas available, which means, it can only run once the engine is at a certain level. The level will be dependent on the model and capacity of the turbocharger. A turbocharger is usually used to increase the power output of an engine, allowing for a similar or greater power output with a smaller engine capacity, a lower capacity will also translates to better fuel economy.
Turbochargers can be divided into two parts, the turbine and compressor, both are connected through a shaft. The turbine of a turbocharger utilize the pressure of the exhaust gas from the engine to spin the shaft, the spinning of the shaft allows the compressor blades to spin as well (since they are connected) and thus able to suck in and compress the air before entering the engine.
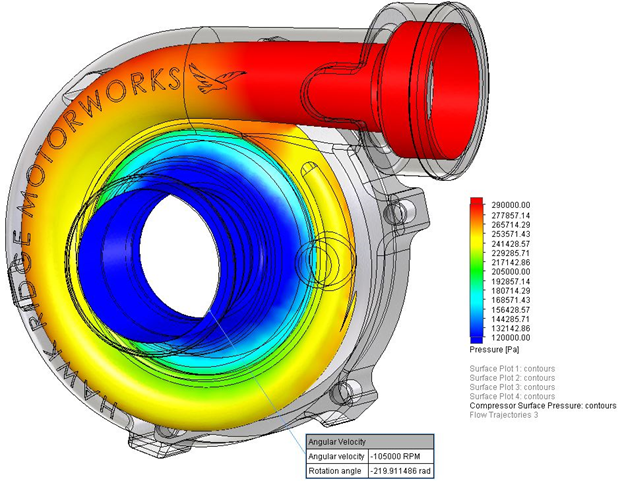 (Image provided by https://hawkridgesys.com/)
(Image provided by https://hawkridgesys.com/)
Here is a pressure simulation example of the turbine side of a turbocharger. A difference in pressure is clearly visible between the inlet and outlet. The difference in pressure of each blade eventually results in the rotational force of the shaft. The utilization of pressure makes these types of turbine a reaction turbine.
Pneumatic and Hydraulic
Pneumatic and hydraulic systems works in a relatively similar way, the difference is with the fluid that are used. Pneumatic systems uses gasses while hydraulic system uses liquid. The important characteristic of both systems is the utilization of pressure.
Some examples of hydraulic system:
- Car trunks as well as engine bay.
- Forklift
- Brake
- Car wash
- etc.
Some examples of pneumatic system:
- Compressed air operated tools (grinder, drill, impact driver)
- Air brakes
- Jackhammer
- Pressure switch
The basic equation that can be used to understand hydraulic is P1 = P2, F1 * A1 = F2 * A2. With the most common concept to learn is from a car wash system.
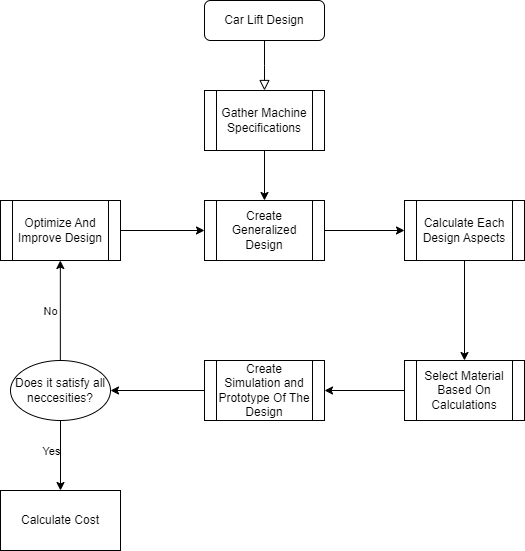
Car Lift Design
- Gather machine specification
- Create generalized design
- Calculate each design aspects
- Select material based on the calculation
- Create simulation and prototype of the design
- Optimize and improve the design
- Calculate cost of production
Specification:
Bed area = (3000 x 680) mm
Lift capacity = 2 Tons
Design: Simple hydraulic car lift system
Initial calculation:
Steam Turbine
Video link:
- Part 1: https://www.youtube.com/watch?v=_fnT_-dDyrg
- Part 2: https://www.youtube.com/watch?v=Ujn9QSXaL-c
- Revision: https://www.youtube.com/watch?v=Mvq7-HabLhc
Conscious Thinking
- Establish Intention
= To learn and study about the concept of steam turbine.
= Learn about the calculation of steam turbine calculation.
- Questions
= How does the steam turbine work?
= What cycle does the steam turbine uses?
= What values are necessary for efficiency calculation?
= What is the purpose of each devices?
- Develop model
= A steam turbine is built using a turbocharger. (physical model)
= A calculation/equation model is created. (calculation/equation model)
- Develop solution steps
= Create a flowchart to represent the solution steps.
Basic Theory
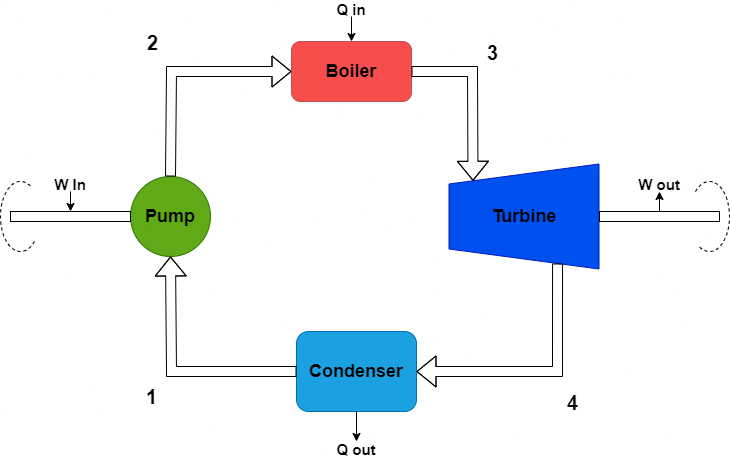
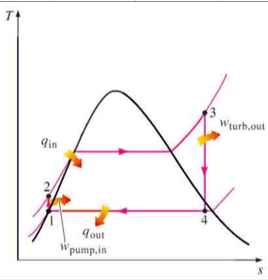
A steam turbine system can be represented using an ideal Rankine cycle. An ideal Rankine cycle is made up for four parts:
- Pump
- Boiler
- Turbine
- Condenser
And it can be divided into 4 stages:
- 1-2 [Isentropic compression in the pump]
- 2-3 [Isobaric heat transfer into the boiler]
- 3-4 [Isentropic expansion in the turbine]
- 4-1 [Isobaric heat rejection from the condenser]
Generalization
Due to the differences between the common ideal Rankine cycle and the model, some generalization and assumption is necessary:
- The model of the system is adjusted to match the ideal Rankine cycle.
- Some values of the system is approximated.
- The values from the property tables are obtained using interpolation unless it is not possible.
Although, if the calculation is solely based on the model:
- To create a more accurate representation of the system, a much more elaborate measurement equipment is necessary to understand the behavior of the system.
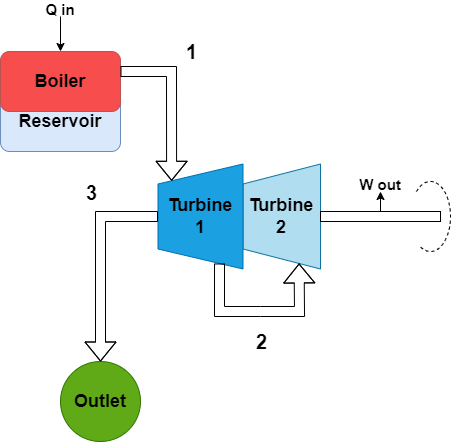
- The system starts with the boiler & reservoir in the same stage -> Turbine 1 -> Turbine 2 -> Outlet.
- Pressure, temperature, enthalpy, entropy is needed in order to create the diagram and calculate the efficiency.
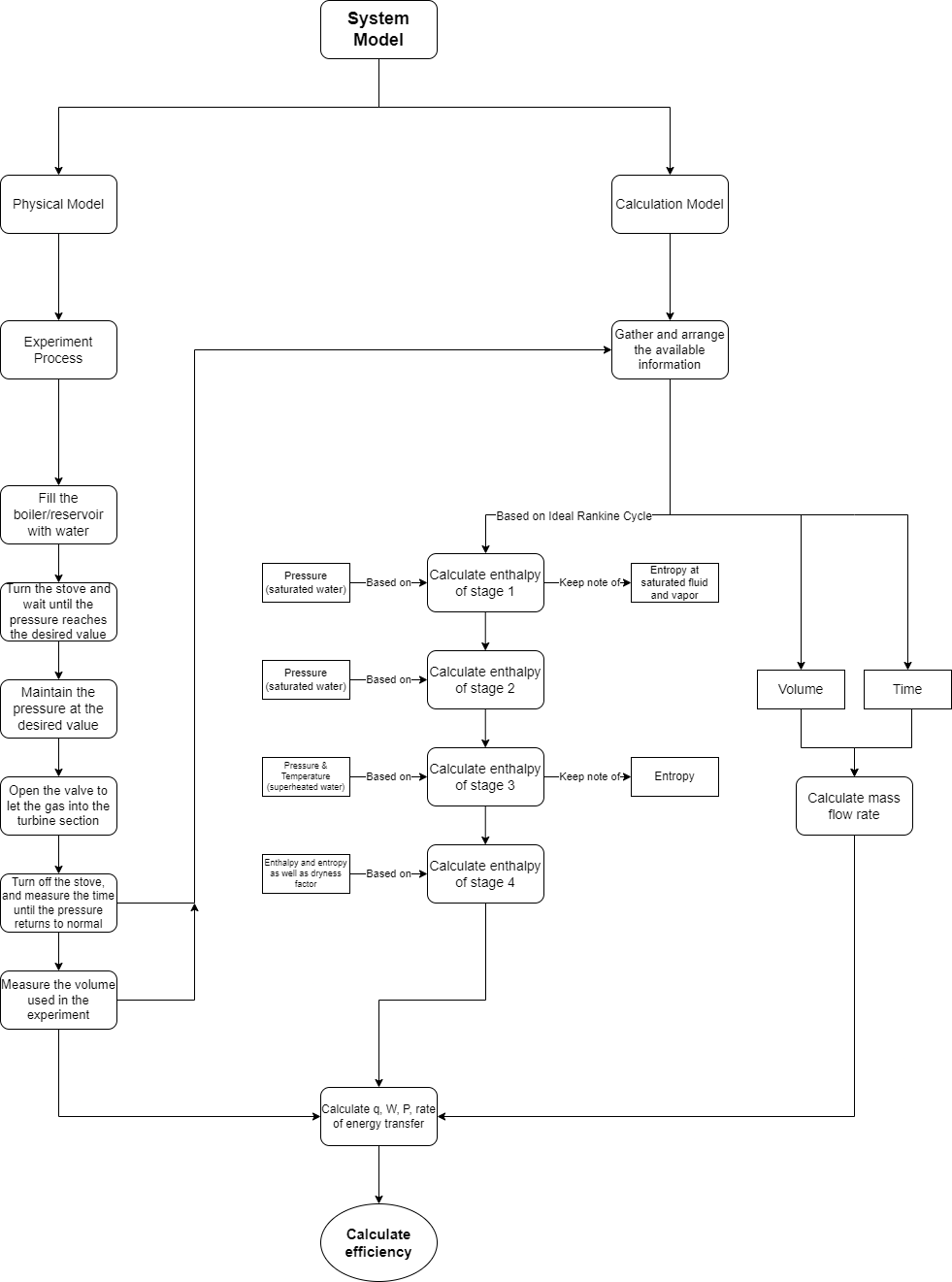
Calculation
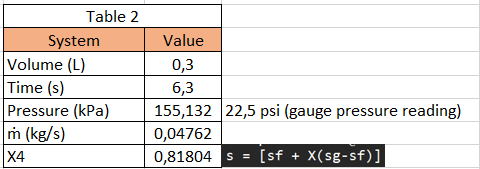
- Volume = 300 ml
- Time = 6,3 s
Before calculating the values, there are a few assumptions that are necessary:
- Generalize the machine to match the conventional Rankine cycle
- Enthalpy value of stage 2 is calculated based on the pressure from the property table
- Temperature is purely based on estimation
- P1 = P4 & P2 = P3
- Based on ideal Rankine cycle
Furthermore, When energy is inputted into the system, the value will be positive. Whenever the energy exits the system, the value will be positive.
To help calculate the efficiency of the system, a spreadsheet is created. Generally, the spreadsheet consists of 3 main tables, which are grouped based on the relevancy of the variables/parameters that are available.
The first table is useful in organizing the value of enthalpy based on the values of pressure. The table also contains values of temperature and entropy.
The second table contains information about the value of the system such as mass flow rate, volume, and pressure.
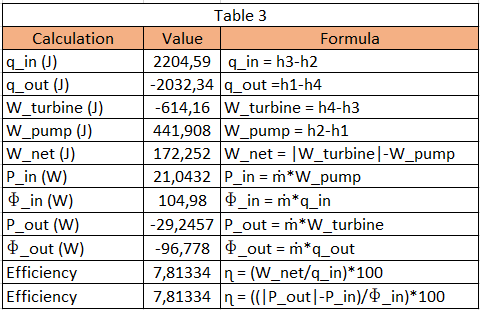
The third table presents the calculation of heat, work, power, energy transfer, and also efficiency.
Diagram
After calculating the values, a flowchart of the steps can be drawn.
Conclusion
- The volume and time of the system only affects the power input and output. It does not affect the efficiency of the system.
= From the table, the power of the system is:
- 21,0432381 W
- -29,24571288 W
- The efficiency of the system can be calculated using two different methods (work with heat or power with rate of energy transfer). With both yields equal result.
- 7,813337113 %
- 7,813337113 %
Although the efficiency is relatively low, it is still quite remarkable since the model originates from a turbocharger which is converted into a steam turbine generator.
Self-assessment
In the course of the Energy Conversion System classes, I always believed that I am doing the best I can possibly do to learn, study, and understand the materials. However I also knew, that it is probably not true for some of the time. Therefore it is necessary to try to improve the effort a little bit more.
In addition, aside from the case mentioned above, generally there still need some improvements with regards to the level of effort and thinking in order to create and open a better future.
Learning about conscious thinking also made me realize, the importance of intention, because without intention, we are often lost and are confused about what we should or should not do and what we need or needn't do.
It is important to always improve, and one step towards improvement is the recognition of our own mistakes. Self assessment is a great way to recognize our mistakes and downsides.