Ayudya Arindari Murahardjo
Contents
[hide]Introduction
Halo!
Perkenalkan, nama saya Ayudya Arindari Murahardjo, akrab disapa Arin. Saya merupakan mahasiswa semester 4 Program Studi Teknik Perkapalan Universitas Indonesia.
Resume Pertemuan 1 (26/5/2023)
Pada pertemuan pertama mata kuliah Metode Numerik, saya belajar mengenai pemahaman tentang "cosciousness", yakni semua orang harus memiliki kesadaran dalam melakukan segala sesuatu termasuk mempelajari Metode Numerik. Terdapat study case pada pertemuan pertama, yaitu mahasiswa diminta untuk menyelesaikan persamaan (x-1)^2/x-1 jika x=1. Pada hal ini, tidak terdapat jawaban yang mutlak atau eksak (1 solusi) karena pada hakikatnya di dalam dunia ini tidak terdapat suatu hal yang pasti.
Semakin kita dewasa, kita semakin kian mengerti akan arti hidup ini, begitu juga dengan kepercayaan yang selama ini kita anut. Mungkin sebagian besar orang memiliki pemahaman yang mereka yakini itu benar dan tidak ada salahnya memilih jalan hidup masing-masing selagi kita tetap "conscious"
Design & Optimization of Pressurized Hydrogen Storage
Design & optimization of pressurized hydrogen storage with maximum cost Rp 500.000,-
Capacity
Volume : 1 liter
Pressure : 8 bar
WEEK 1 PROGRESS
Designing and optimizing a pressurized hydrogen storage system with a 1-liter capacity and 8-bar pressure within a budget of Rp 500.000,- involves careful consideration of materials, dimensions, and cost optimization. Here's a design and optimization approach:
Material Selection
To meet the budget constraint, consider using high-density polyethylene (HDPE) as the material for the storage system. HDPE is cost-effective and offers good chemical resistance.
Container Design
Shape: Design a cylindrical container, as it is a common and practical shape for pressurized storage. Dimensions: Determine the container dimensions based on the desired volume and pressure. The container's volume is fixed at 1 liter, and the pressure is 8 bar.
Wall Thickness: Calculate the required wall thickness using the Barlow's formula: t = (P * D) / (2 * S), where P is the pressure (8 bar), D is the diameter of the container, and S is the allowable stress for HDPE. Ensure the calculated wall thickness is within the manufacturing capabilities and budget constraints.
Optimization Strategies
Material Cost: Compare prices from different HDPE suppliers to select the most cost-effective option. Manufacturing Process: Consider extrusion or injection molding processes for HDPE container fabrication, as they can be cost-effective for producing cylindrical shapes.
Size Optimization: Optimize the dimensions of the container to minimize material usage and manufacturing costs while still meeting the required volume and pressure specifications. This can be achieved by adjusting the diameter and height of the container.
Safety Considerations: Incorporate safety features into the design, such as pressure relief devices and adherence to safety standards and regulations for hydrogen storage.
Final Result Design & Optimization of Pressurized Hydrogen Storage
Fundamental Steps
To calculate the design of an optimal hydrogen storage tube with a 1-liter volume and 8-bar pressure specification, we can follow these steps:
1. Determine the desired dimensions: Since the volume and pressure specifications are given, the next step is to calculate the dimensions of the storage tube.
2. Convert the volume to cubic meters: 1 liter is equal to 0.001 cubic meters.
3. Convert the pressure to pascals: 1 bar is equal to 100,000 pascals.
4. Apply the ideal gas law: The ideal gas law equation, PV = nRT, can be used to calculate the volume of the storage tube. However, we need additional information such as the number of moles of hydrogen (n) and the temperature (T) to proceed with the calculation. Without this information, we cannot determine the exact dimensions of the storage tube.
5. Consider the material and safety factors: Once you have the necessary dimensions, you will need to select a suitable material that can withstand the pressure and store hydrogen safely. Materials such as high-strength steel or composite materials may be considered.
Material Selection
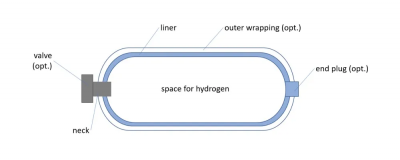
Based on the type of material, hydrogen storage tank are divided into four types as shown in the following image. I have chosen the fourth type, which utilizes two different materials. For the outer material, I am using HDPE plastic, and for the inner material, I am using stainless steel AISI 304. The use of the fourth type is expected to be the most suitable for this design because the chosen materials are highly effective and efficient in their use.
High-Density Polyethylene (HDPE) is a commonly used material for various applications, including hydrogen storage tanks. When designing a hydrogen storage tank using HDPE, several safety factors should be considered:
1. Material Compatibility HDPE is known for its excellent chemical resistance, including resistance to hydrogen gas. However, it is important to verify the specific grade of HDPE being used and ensure its compatibility with hydrogen. The material supplier should provide information regarding the suitability of the HDPE grade for hydrogen storage.
2. Pressure Rating HDPE tanks must be designed to withstand the pressure generated by the stored hydrogen. The pressure rating of the HDPE material should be considered, along with the required safety factors, to ensure the tank's structural integrity. The design should conform to relevant standards or codes for pressure vessel design.
3. Temperature Considerations HDPE has a temperature limitation, and the operating temperature of the hydrogen storage tank should be within the specified range for the HDPE material. Elevated temperatures can affect the mechanical properties of HDPE, potentially reducing its strength and impact resistance. Adequate insulation or cooling measures may be required to maintain the temperature within the acceptable range.
4. Hydrogen Permeation While HDPE is considered a barrier material, it is still necessary to consider the potential permeation of hydrogen through the material over time. HDPE is known to have relatively low permeability to hydrogen, but precautions should be taken to minimize the risk. This can include measures such as proper thickness of the HDPE walls and considering additional barrier layers or coatings, if required.
5. Stress Concentrations Care must be taken to avoid stress concentrations in the tank design, as they can lead to premature failure. Smooth transitions, rounded corners, and proper reinforcement in areas prone to stress concentration should be considered to distribute stresses and minimize the risk of failure.
6. Manufacturing and Welding If the HDPE tank requires welding or fabrication, it is essential to follow proper welding techniques and procedures specific to HDPE. Qualified welders should be employed, and welding inspections should be conducted to ensure the quality and integrity of the welds.
For inner material, we use stainless steel AISI 304
AISI 304 is a widely used stainless steel grade that offers excellent corrosion resistance, high durability, and good mechanical properties. It is commonly referred to as 18/8 stainless steel, as it contains 18% chromium and 8% nickel. AISI 304 is non-magnetic and exhibits good formability, making it suitable for a wide range of applications, including food processing equipment, kitchen appliances, chemical containers, and architectural trim.
In terms of material safety, AISI 304 is considered to be a relatively safe material to use. Here are some key points regarding its safety:
Corrosion Resistance: AISI 304 stainless steel is highly resistant to corrosion in a variety of environments, including atmospheric conditions, freshwater, and mild chemical environments. This corrosion resistance helps prevent the release of harmful substances into the surroundings.
Non-Toxicity: AISI 304 stainless steel is non-toxic and does not leach any harmful substances into food or other materials it comes into contact with. This property makes it suitable for use in food processing and medical applications.
Hygiene: Due to its smooth surface finish, AISI 304 is easy to clean and maintain hygiene standards. It resists bacterial growth and is often used in environments where cleanliness is crucial, such as hospitals and kitchens.
Compatibility: AISI 304 is compatible with a wide range of materials and can safely interact with various chemicals, solvents, and cleaning agents without undergoing significant degradation or releasing harmful byproducts.
While AISI 304 stainless steel is generally safe, it's important to note that certain fabrication processes, such as welding or grinding, can release small particles or fumes that may be hazardous to health. Proper safety precautions, such as using personal protective equipment (PPE) and adequate ventilation, should be followed when working with or processing AISI 304 stainless steel to minimize any potential risks.
Overall, AISI 304 stainless steel is a widely used and safe material choice for many applications, thanks to its excellent corrosion resistance, non-toxicity, and hygienic properties. However, as with any material, it is essential to handle, process, and use it responsibly while adhering to appropriate safety guidelines.
By combining HDPE and AIS 304 stainless steel, the hydrogen cylinder benefits from the chemical resistance and lightweight nature of HDPE, while the stainless steel inner layer provides corrosion resistance, strength, and temperature stability. This combination offers a well-rounded solution that takes advantage of the strengths of both materials.
Geometric Calculation
Outer Material (HDPE)
1. Thickness
import math
def calculate_optimized_thickness(volume, pressure): # Material properties of HDPE yield_strength = 22 # MPa (Megapascal) safety_factor = 2 # Safety factor for design # Conversion factors mpa_to_bar = 10 # 1 MPa = 10 bar # Convert pressure to MPa pressure_mpa = pressure / mpa_to_bar # Calculate optimized thickness thickness = (volume * pressure_mpa) / (2 * math.pi * yield_strength * safety_factor) # Convert thickness to millimeters thickness_mm = thickness * 1000 return thickness_mm
# Specify the volume and pressure volume = 1 # Liter pressure = 8 # bar
# Calculate optimized thickness optimized_thickness = calculate_optimized_thickness(volume, pressure)
# Print the result
print(f"The optimized thickness of HDPE for {volume} liter capacity and {pressure} bar pressure is approximately
{optimized_thickness:.2f} mm.")
Based on calculation the minimum thickness get 2.89 mm In this code, we assume a yield strength of 22 MPa for HDPE and use a safety factor of 2 for design purposes. The calculate_optimized_thickness function takes the volume and pressure as input and returns the optimized thickness in millimeters.
2. Radius and Height
import math
def calculate_optimized_dimensions(volume, pressure): # Material properties and safety factor for HDPE yield_strength = 22 # MPa (Megapascal) safety_factor = 2 # Safety factor for design # Conversion factors mpa_to_bar = 10 # 1 MPa = 10 bar # Convert pressure to MPa pressure_mpa = pressure / mpa_to_bar # Calculate the radius radius = math.sqrt((volume * pressure_mpa) / (math.pi * yield_strength * safety_factor)) # Calculate the height height = 2 * radius # Convert radius and height to millimeters radius_mm = radius * 1000 height_mm = height * 1000 return height_mm, radius_mm
# Specify the volume and pressure volume = 1 # Liter pressure = 8 # bar
# Calculate optimized dimensions optimized_height, optimized_radius = calculate_optimized_dimensions(volume, pressure)
# Print the result
print(f"The optimized height and diameter of the HDPE hydrogen storage vessel for {volume} liter capacity and {pressure} bar pressure are
approximately {optimized_height:.2f} mm and {optimized_radius:.2f} mm, respectively.")
In this code, we calculate the radius of the vessel based on the volume and pressure using the formula derived from the cylinder volume equation. The height is then calculated as twice the radius. Both the height and radius are converted to millimeters for display purposes. Based on this calculation, the height and the radius are 152.15 mm and 76.08 mm
3. The Surface Area of HDPE
import math
def calculate_surface_area(height, diameter, thickness): # Convert dimensions to millimeters height_mm = height diameter_mm = diameter thickness_mm = thickness # Calculate inner radius radius_inner = (diameter_mm / 2) - thickness_mm # Calculate outer radius radius_outer = diameter_mm / 2 # Calculate surface area area_inner = 2 * math.pi * radius_inner * height_mm area_outer = 2 * math.pi * radius_outer * height_mm area_top_bottom = math.pi * (radius_outer**2 - radius_inner**2) total_surface_area = area_inner + area_outer + area_top_bottom return total_surface_area
# Specify the dimensions in millimeters height = 152.15 diameter = 76.08 thickness = 2.89
# Calculate the surface area surface_area = calculate_surface_area(height, diameter, thickness)
# Print the result
print(f"The surface area of the cylindrical vessel is approximately {surface_area:.2f} square millimeters.")
In this code, the calculate_surface_area function takes the height, diameter, and thickness as input. It converts the dimensions to meters and then calculates the inner and outer radii. The surface area is calculated by considering the cylindrical sides, top, and bottom of the vessel. The total surface area is the sum of the areas of the inner and outer cylindrical surfaces and the top and bottom circular surfaces. Based on this calculation, the minimal surface area is 70633.17 mm^2 or 706.3317 cm^2
Inner Material (AISI 304)
1. Thickness
import math
def calculate_optimized_thickness(volume, pressure): # Material properties of mild steel yield_strength = 250 # MPa (Megapascal) safety_factor = 3 # Safety factor for design # Conversion factors mpa_to_bar = 10 # 1 MPa = 10 bar # Convert pressure to MPa pressure_mpa = pressure / mpa_to_bar # Calculate optimized thickness thickness = (volume * pressure_mpa) / (2 * math.pi * yield_strength * safety_factor) # Convert thickness to millimeters thickness_mm = thickness * 1000 return thickness_mm
# Specify the volume and pressure volume = 1 # Liter pressure = 8 # bar
# Calculate optimized thickness optimized_thickness = calculate_optimized_thickness(volume, pressure)
# Print the result
print(f"The optimized thickness of mild steel for {volume} liter capacity and {pressure} bar pressure is approximately
{optimized_thickness:.2f} mm.")
In this code, we assume a yield strength of 250 MPa for stainless steel and use a safety factor of 3 for design purposes. The calculate_optimized_thickness function takes the volume and pressure as input and returns the optimized thickness in millimeters. Based on this calculation, the thickness of AISI 304 is 0.20 mm
2. Radius and Height of AISI 304
Inner Height = 152.15 mm - 2.89 mm = 149.26 mm
Inner Radius = 76.08 mm -2 .89 mm = 73.19 mm
3. The Surface Area
import math
def calculate_surface_area(height, diameter, thickness): # Convert dimensions to millimeters height_mm = height diameter_mm = diameter thickness_mm = thickness # Calculate inner radius radius_inner = (diameter_mm / 2) - thickness_mm # Calculate outer radius radius_outer = diameter_mm / 2 # Calculate surface area area_inner = 2 * math.pi * radius_inner * height_mm area_outer = 2 * math.pi * radius_outer * height_mm area_top_bottom = math.pi * (radius_outer**2 - radius_inner**2) total_surface_area = area_inner + area_outer + area_top_bottom return total_surface_area
# Specify the dimensions in millimeters height = 149.26 diameter = 73.218 thickness = 0.2
# Calculate the surface area surface_area = calculate_surface_area(height, diameter, thickness)
# Print the result
print(f"The surface area of the cylindrical vessel is approximately {surface_area:.2f} square millimeters.")
The surface area of the cylindrical vessel is approximately 68484.19 square millimeters or 684.8419 cm^2
Cost Calculation
The inner surface area with Stainless Steel AISI 304 material = 684.8419 cm^2
The outer surface area with HDPE material = 706.3317 cm^2
Based on marketplace (Tokopedia), the price of AISI 304 material 3 mm x 330 mm x 330 mm or 326700 mm^2 is Rp 423.000,- So, the cost for 68484.19 mm^2 is Rp 88.670,-
Based on marketplace (Tokopedia), the price of HDPE material 0.3 cm x 100 cm x 200 cm or 6000 cm^2 is Rp 550.000,- So, the cost for 706.3317 cm^2 is Rp 64.747,-
Based on marketplace (Tokopedia), the price of Air Compressor Regulator Valve 1/4" Pressure Gauge 140psi (8 bar) is Rp 99.961,-
The total cost to manufactured hydrogen storage tank is Rp 253.378,-