Andika Ramadhan Gurnida
Nama : Andika Ramadhan Gurnida NPM : 1506742943 Hobi : Panjat Tebing, Musik
Contents
[hide]Pertemuan 1
Pada pertemuan ini para mahasiswa di kelas Metnum-02 diperkenalkan dengan web air.eng.ui.ac.id . Web yang dibuat oleh Pak DAI itu digunakan untuk mengupload tugas-tugas selama kuliah metode numerik ini. Pada pertemuan ini kami diajarkan cara membuat page, dimana post pertama kami adalah "mengapa kita harus belajar kalkulus"
Metoda numerik merupakan bagian dari ilmu matematika. Numerik dapat digunakan sebagai pemecah masalah bagi mereka yang sudah memiliki ide, namun saja perhitungan akan sangat banyak. Pada mata kuliah ini, bahasa pemrograman yang akan digunakan merupakan Python
Pertemuan 2
Pada pertemuan ini dijelaskan tentang bahasa pemrograman Python. Keuntungan dari Python sendiri antara lain: 1. Merupakan software yang bersifat open-source, 2. Tersedia untuk major operating system, 3. Lebih mudah untuk dipelajari, 4. Mudah untuk diinstall
AI merupakan rekayasa yang dibuat oleh manusia untuk membantu manusia tersebut. Manusia membutuhkan AI dikarenakan kemampuannya yang terbatas, terutama dalam memproses angka yang sangat banyak jumlahnya, kemudian juga manusia mempunyai kemampuan menghapal yang lemah. Contohnya apabila manusia bermain catur melawan komputer, tentunya komputer tersebut akan meaning dikarenakan sudah menyimpan sejumlah database gerakan. Namun perbedaan manusia dengan AI yang terbesar adalah manusia mempunyai hati.
Pak DAI juga menyampaikan bahwa industri 5.0 adalah pancasila karena seharusnya teknologi tidak membodohi dan melemahkan manusia, tetapi harus membantu manusia.
Di akhir kelas kami diberi tugas untuk membuat "Hello World" menggunakan bahasa pemrograman Python.
Pertemuan 3
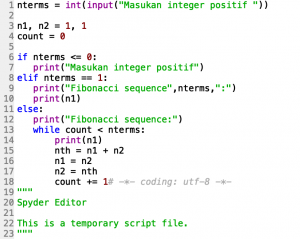
Pada pertemuan ketiga kami diberi tugas untuk membuat program untuk menyelesaikan deret fibonacci :
Syntax
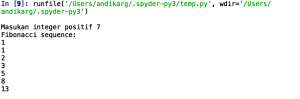
Hasil
Headline text
QUIZ 2
#ProbSet 2.1 no.6
#jawaban
from numpy import linalg
import numpy as np
#Definisi
row1 = [0,0,2,1,2]
row2 = [0,1,0,2,-1]
row3 = [1,2,0,-2,0]
row4 = [0,0,0,-1,1]
row5 = [0,1,-1,1,-1]
nmat = np.array([row1,row2,row3,row4,row5])
print("n matrix are:")
print(nmat)
cons = np.array([1,1,-4,-2,-1])
print("Y matrix are:")
print(cons)
#Penyelesaian
Ans = linalg.solve(nmat,cons)
x1val=int(Ans[0])
x2val=int(Ans[1])
x3val=int(Ans[2])
x4val=int(Ans[3])
x5val=int(Ans[4])
print("x result are:")
print("x1=",x1val)
print("x2=",x2val)
print("x3=",x3val)
print("x4=",x4val)
print("x5=",x5val)
Ujian Tengah Semester
'''No.1''' from math import *
g = 9.81
m1 = eval(input("mass 1: "))
m2 = eval(input("mass 2: "))
m3 = eval(input("mass 3: "))
alpha = eval(input("alpha: "))
u = eval(input("friction coefficient: "))
x = sin(alpha)
y = cos(alpha)
t1 = m1*g*(x-(u*y))
t2 = (m2*g*(x-(u*y))) + t1
t3 = (m3*g*(x-(u*y))) + t2
t4 = t3
#Hasil
print("t1: ",t1)
print("t2: ",t2)
print("t3: ",t3)
print("t4: ",t4)
from math import *
from sympy import *
g = 9.81
pro = 1.2
cd = eval(input("drag coefficient: "))
area = eval(input("area : "))
v0 = 0
m = eval(input("car mass: "))
u = eval(input("friction: "))
a = eval(input("acceleration: "))
vt = eval(input("top speed: "))
fs = g*u
fdrag= (cd*area*pro*v0**2)/2*m
f1 = a
atot = f1 - (fdrag + fs)
t = (vt-v0)/atot
print("time to reach top speed : ",t)
Video Muhasabah : https://youtu.be/RUl5zqLGhoE
Perbaikan UTS
Perbaikan kasus A dengan menggunakan metode eliminasi Gauss :
import math
import numpy as np
#matrix C & D
C = np.array([[1., 0., 0.],
[-1., 1., 0.],
[0., -1., 1.]], float)
D = np.array([21.37, 14.24, 7.12], float)
n = len(C) #panjang dari baris c
print('Matriks C :')
print(C,'\n')
print('Matriks C mempunyai ', n , ' baris','\n')
print('Matriks D :')
print(D,'\n')
for k in range(0,n-1): #menggunakan metode eliminasi gauss
for i in range(k+1,n):
if C[i,k]!=0 :
lam = C[i,k]/C[k,k]
C[i,k:n] = C[i,k:n]-(C[k,k:n]*lam)
D[i] = D[i]-(D[k]*lam)
print('matrix C:', '\n', C, '\n')
print('Nilai tegangan tali :')
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(D[m]-np.dot(C[m,m+1:n],x[m+1:n]))/C[m,m]
print('T',m+1,'=', x[m])
Kasus B dengan menggunakan metode Runge Kutta :
g = 9.81
u = eval(input("Friction Coefficient: "))
a = eval(input("Percepatan mobil : "))
cd = eval(input("Drag coefficient : "))
m = eval(input("Massa mobil : "))
t0 = 0
v0 = 0
dt = 1
error = 100
F = a - g*u #dibagi dengan massa
fs = cd/m #dibagi dengan massa
lst = []
def dvdt(t0, v0):
return F-(fs*(v0)**(1.5))
while error > 0.005:
k1 = dvdt(t0, v0)
k2 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k1)
k3 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k2)
k4 = dvdt(t0 + dt, v0 + dt * k3)
v1 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
t0 = t0 + dt
error = ((v1 - v0) / v1)*100 #persentase error
v0 = v1
lst.append(v1)
waktu = len(lst)
print ("Waktu yang dibutuhkan mobil untuk mencapai top speed dari diam: ", waktu+1, "s")
print ("top speed: ", v1, "m/s")
Pertemuan ke - 10
Pada pertemuan ini Pak Dai membahas mengenai soal UTS kemarin. Dalam menjawab soal UTS, kami diminta menuliskan percepatan dalam menghitung terminal velocity namun pada realitanya dalam penjualan mobil, spesifikasi percepatan tidak ada. Untuk itu, kami disarankan untuk mengerjakan ulang soal UTS tersebut dan menambahkan data horsepower dan RPM mobil tersebut.
Pertemuan ke - 11
Pada pertemuan ini diberikan materi mengenai regresi linier, curve fitting, dan least square. Ketiga hal ini berguna untuk membantu mencari optimasi pada suatu fungsi. Optimasi ini sendiri adalah metode yang digunakan untuk mencari nilai optimum dengan mencari nilai minimum atau maksimum dari suatu fungsi. Fungsi yang diberikan bisa berupa persamaan yang sudah dicari atau ditemukan. Fungsi bisa didapatkan dengan menggunakan curve fitting. Cara penggunaannya dari membuat curve fitting lalu mengambil persamaan dari curve fitting tersebut. Persamaan ini bisa digunakan dalam Python untuk melakukan optimasi.
Pertemuan ke - 12
Pada pertemuan keduabelas kelas Metode Numerik ini, kelas diisi oleh Bang Edo. Bang Edo memperkenalkan kepada kami sebuah software CFD (Computational Fluid Dynamics) bernama CFDSOF_NG. Bang Edo mengajarkan kami cara menggunakan software dab menyediakan contoh untuk kami analisis, yaitu body dari sebuah mobil. Dalam pengoperasian CFDSOF_NG ini, banyak sekali variabel yang diatur. Mulai dari bentuk mesh, mesh point, karakteristik fluida, boundaries aliran fluida, serta metode analisanya.
Untuk dapat melakukan analisis CFD ini, tentu kami harus mengunduh software CFDSOF_NG ini sendiri. Kami mengunduh CFDSOF_NG di CFDSOF. Setelah kami mengunduhnya, kami melakukan instalasi software dan melakukan analisis terhadap body mobil. Hasil analisis ini adalah berupa tampak visual persebaran tekanan diseluruh permukaan body. Lalu kami diberikan tugas untuk menganalisis gaya-gaya yang ada di body mobil dan kemudian menggunakan metode curve fitting dalam pencarian persamaan.
Pertemuan ke-13
Pada pertemuan ketigabelas kelas Metode Numerik ini, kelas diisi oleh Pak Dai. Pak Dai memberikan kami kuis dadakan untuk menguji kesiapan kami dalam memahami metode numerik. Materi kuisnya adalah mengenai tugas yang sudah diberikan pada kami sebelumnya dan tentunya mengenai optimasi.
Pada pertemuan ini juga Bang Edo memberikan kami tugas lagi untuk membuat analisis drag force dan lift force airfoil dengan variasi angle of attack, yang kemudian kami optimisi untuk mendapatkan angle of attack yang paling optimum.
Airfoil
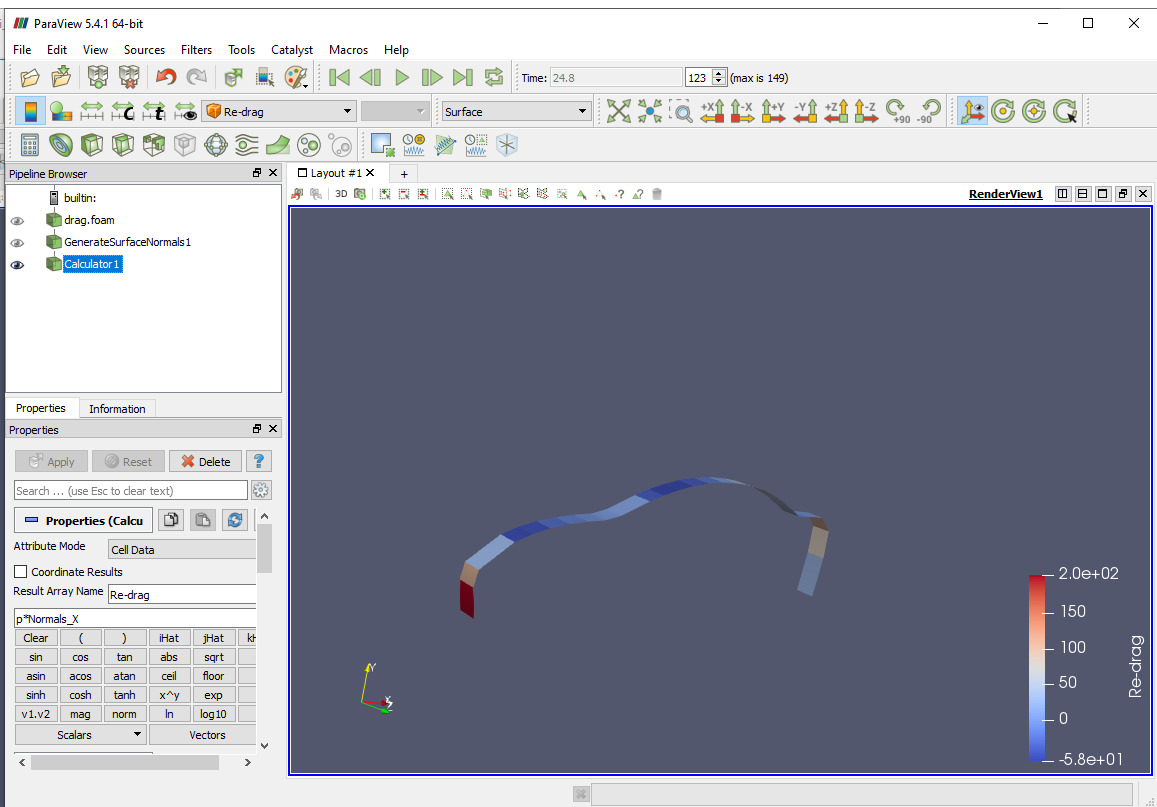
Paraview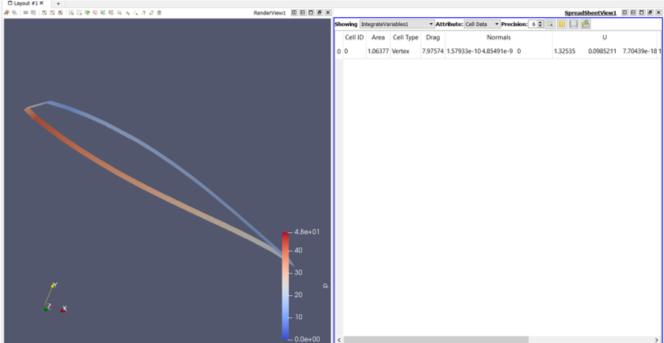
Hasil CFDSOS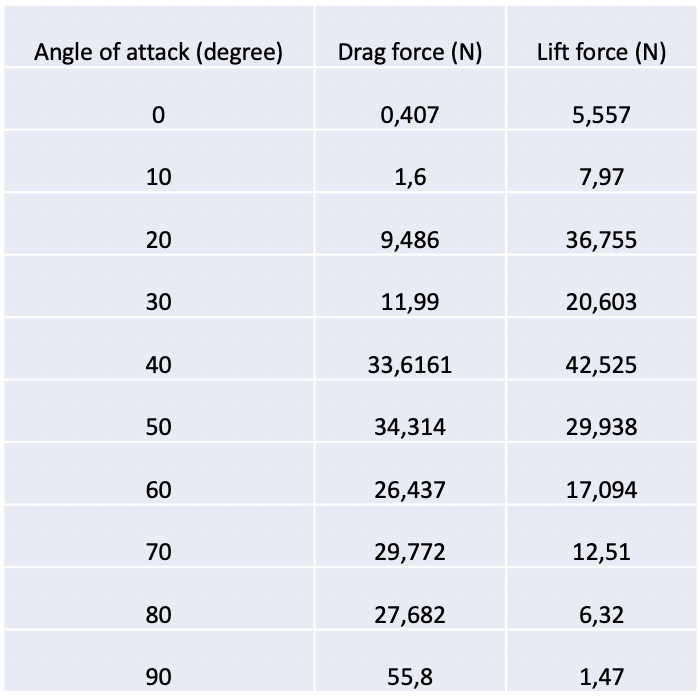
Grafik Hasil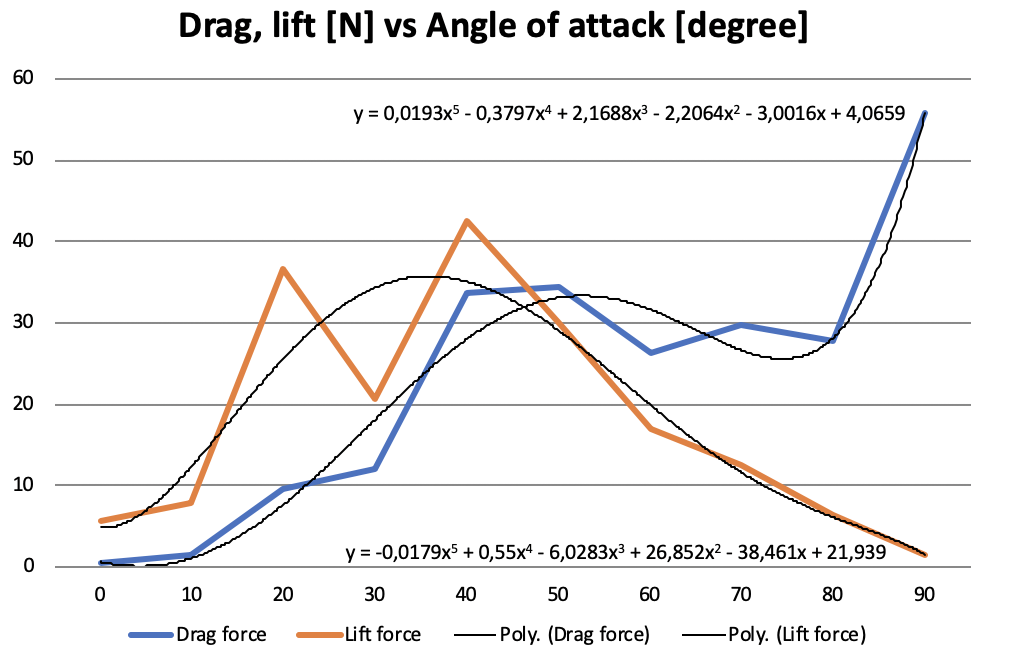
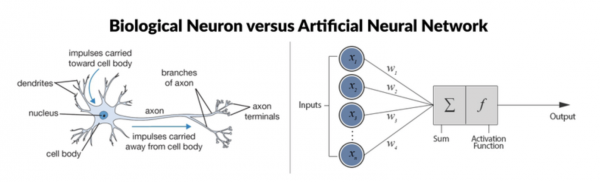
Neural Network
Artificial Neural Network adalah sistem jaringan pembelajaran terawasi yang terdiri dari elemen sederhana. Elemen tersebut adalah neuron dan perceptron. Setiap neuron dapat membuat keputusan sederhana, dan memberi makan keputusan itu ke neuron lain, yang diorganisasikan dalam lapisan yang saling berhubungan.
Back Propagation
Arsitektur algoritma backpropagation terdiri dari tiga layer, yaitu input layer, hidden layer dan output layer. Pada input layer tidak terjadi proses komputasi, namun pada input layer terjadi pengiriman sinyal input X ke hidden layer. Pada hidden dan output layer terjadi proses komputasi terhadap bobot dan bias dan dihitung pula besarnya output dari hidden dan output layer tersebut berdasarkan fungsi aktivasi tertentu. Dalam algoritma backpropagation ini digunakan fungsi aktivasi sigmoid biner, karena output yang diharapkan bernilai antara 0 sampai 1.
Algoritma backpropagation adalah sebuah algoritma untuk memperkecil tingkat error dengan menyesuaikan bobot berdasarkan perbedaan output dan target yang diinginkan. Secara umum algoritmanya terdiri dari tiga langkah utama, yaitu :
a. Pengambilan input
b. Penelusuran error
c. Penyesuaian bobot
Langkah membangun ANN:
1. Data Preprocessing
2. Add input layer
3. Random w init
4. Add Hidden Layers
5. Select Optimizer, Loss, and Performance Metrics
6. Compile the model
7. use model.fit to train the model
8. Evaluate the model
9. Adjust optimization parameters or model if needed