Analisa Struktur Sederhana menggunakan software EES
Nama : Samsul Maarif NPM : 1806244556
Analisa Struktur Pondasi Sederhana
Latihan Soal Minggu ke 2
Analisis struktur sederhana masih dapat dilakukan dengan cara manual, namun realitas di lapangan terdapat banyak struktur yang kompleks dan menuntut analisis secara cepat dan presisi. Perhitungan dan analisis manual membutuhkan waktu yang cukup dan jika terjadi kesalahan harus dilakukan perhitungan ulang yang membutuhkan tambahan waktu lagi. Pemakaian komputer dan aplikasi perhitungan atau yag lebih dikenal sebagai komputasi teknik dapat digunakan untuk mempermudah dan mempercepat perhitungan analisis struktur. Namun pengetahuan dan keahlian analisis struktur mutlak harus dikuasai oleh seorang engineer, sehingga engineer tetap berperan sebagai pemegang kendali dan pembuat keputusan terhadap suatu analisis.
Beberapa keuntungan dalam komputasi teknik antara lain:
- Dapat menganalisis dengan parameter yang ekstrem yang mendekati kondisi ekstrem yang sebenarnya
- Biaya analisis menjadi lebih murah.
- Model benda dapat bervariasi tergantung kebutuhan.
Contoh soal
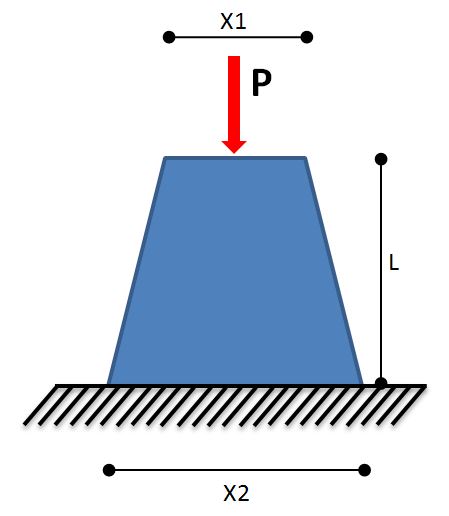
Sebuah pelat meterial homogen diberikan gaya vertikal seperti gambar di samping. Lakukan analisis terhadap fenomena pembebanan pelat dengan pendekatan komputasi teknik.
Konsep Dasar
Sebuah benda yang diberikan gaya akan mengalami perubahan bentuk searah dengan gaya, begitu pula dengan sebuah pelat datar pada aplikasi struktur.
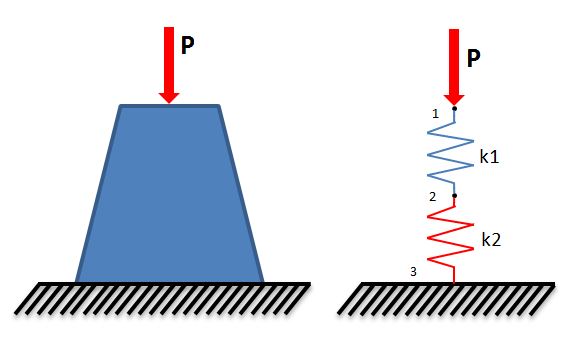
Perubahan bentuk pada kasus ini didefinisikan sebagai displacement (u), dan akan dilakukan pendekatan dengan model pegas sederhana.
Pendekatan model pegas dilakukan dengan model 1 dimensi karena gaya-gaya yang terjadi berada pada suatu sumbu yang sama.
Aplikasi Struktur Menggunakan Model Pegas
Persamaan umum struktur
E= σ/ε= (F/A)/(∆L/L)
F= (EA/L) ∆L
Dimana :
E = Elastisitas
σ = Tegangan
ε = Regangan
F = Gaya
A = Luas Penampang
L = Panjang sejajar gaya
Persamaan umum Pegas
F = k.u
k = Konstanta pegas
u = Perubahan bentuk
Pemodelan :
EA/L=k ∆L=u
Pemodelan 2 pegas
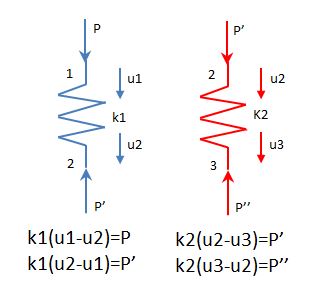
Free Body Diagram
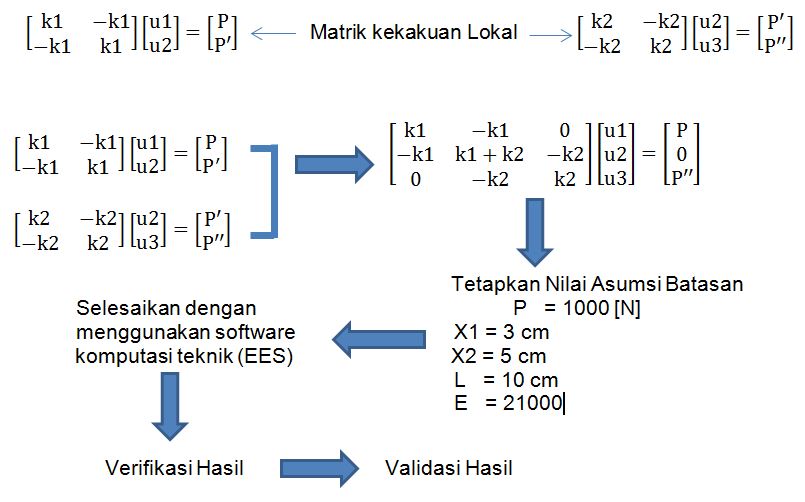
Matrik dan Alur Pengerjaan
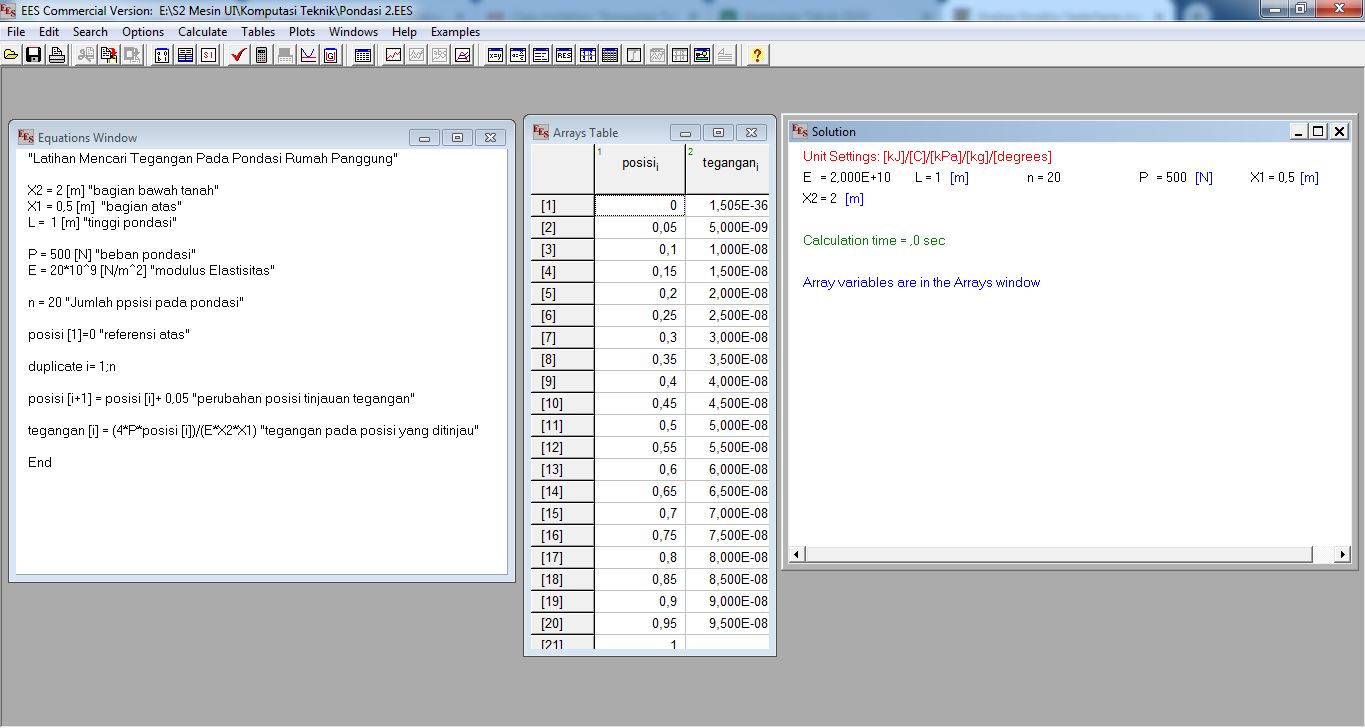
Simulasi EES
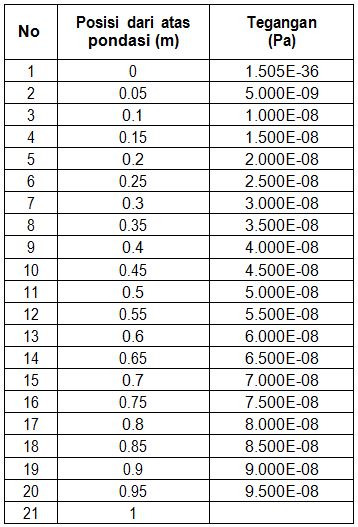
Hasil Perhitungan EES