Aldy Cahya Ramadhan
Aldy Cahya Ramadhan (lahir di Surabaya,26 Desember 2000).Seorang mahasiswa Teknik Mesin angkatan 2018
Contents
[hide]Mengapa Harus Belajar Kalkulus
Karena Kalkulus merupakan dasar dalam mempelajari Pelajaran seperti Termodinamika, Metode Numerik, dan lain lain
PHYTON
Python adalah bahasa pemrograman interpretatif multigunadengan filosofi perancangan yang berfokus pada tingkat keterbacaan kode. Python diklaim sebagai bahasa yang menggabungkan kapabilitas, kemampuan, dengan sintaksis kode yang sangat jelas,dan dilengkapi dengan fungsionalitas pustaka standar yang besar serta komprehensif. Python juga didukung oleh komunitas yang besar.
Python Tuple Programing
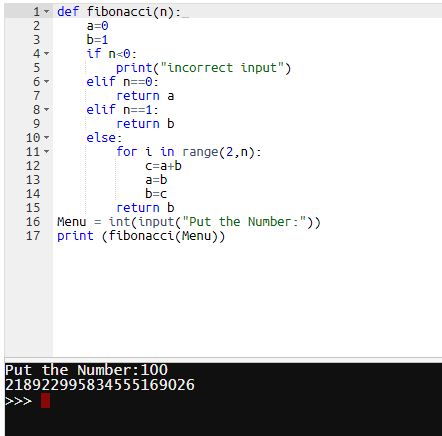
Fibonacci
Dalam matematika, bilangan Fibonacci adalah barisan yang didefinisikan secara rekursif sebagai berikut:
barisan ini berawal dari 0 dan 1, kemudian angka berikutnya didapat dengan cara menambahkan kedua bilangan yang berurutan sebelumnya. Dengan aturan ini, maka barisan bilangan Fibonaccci yang pertama adalah:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946... Barisan bilangan Fibonacci dapat dinyatakan sebagai berikut:
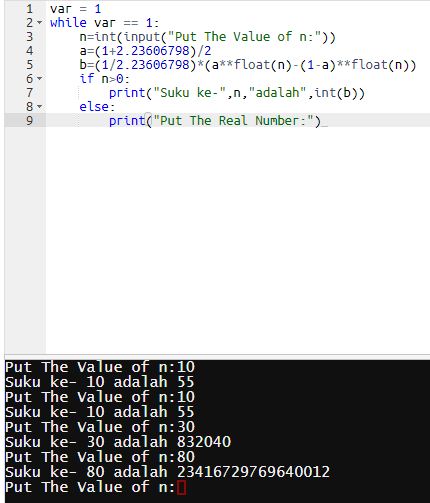
Fn = (x1n – x2n)/ sqrt(5) dengan
Fn adalah bilangan Fibonacci ke-n x1 dan x2 adalah penyelesaian persamaan x2 – x – 1 = 0. Perbandingan antara Fn+1 dengan Fn hampir selalu sama untuk sebarang nilai n dan mulai nilai n tertentu, perbandingan ini nilainya tetap. Perbandingan itu disebut rasio emas yang nilainya mendekati 1,618.
1.Fibonacci with Recursion/Loop
2.Fibonacci with Function
Solusi soal SET 2.1 NO.6 Hal 55
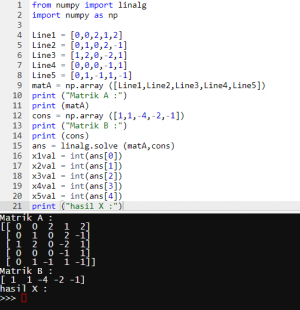
Input : from numpy import linalg import numpy as np
Line1 = [0,0,2,1,2] Line2 = [0,1,0,2,-1] Line3 = [1,2,0,-2,1] Line4 = [0,0,0,-1,1] Line5 = [0,1,-1,1,-1] matA = np.array ([Line1,Line2,Line3,Line4,Line5]) print ("Matrik A :") print (matA) cons = np.array ([1,1,-4,-2,-1]) print ("Matrik B :") print (cons) ans = linalg.solve (matA,cons) x1val = int(ans[0]) x2val = int(ans[1]) x3val = int(ans[2]) x4val = int(ans[3]) x5val = int(ans[4]) print ("hasil X :")
Output : Matrik A : [[0 0 2 1 2]
[0 1 0 2 -1] [1 2 0 -2 1] [0 0 0 -1 1] [0 1 -1 1 -1]]
Matrik B : [1 1 -4 -2 -1] hasil X : x1= 3 x2=-2 x3= 1 x4= 1 x5=-1
NO 2 Hal 255
Input : def dydx(x, y):
return ((x**2 - 4*y))
def RungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
x0 = 0 y = 1 x = 0.03 h = 0.01 print ('Nilai y di x adalah :', RungeKutta(x0, y, x, h))
Output : Nilai y di x adalah : 0.8869291754400297
UTS
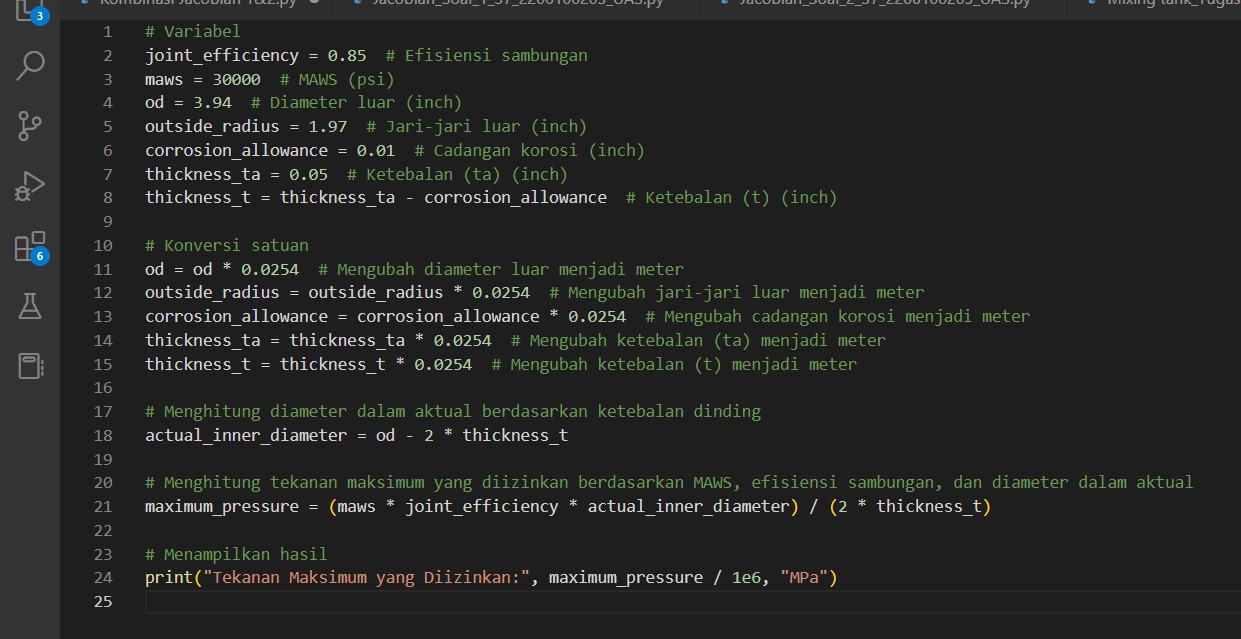
NO 1
import math
G = 9.81
M1 = float(input("Massa 1 :"))
M2 = float(input("Massa 2 :"))
M3 = float(input("Massa 3 :"))
M4 = float(input("Massa 4 :"))
P = float(input("Koefisien Gesek :"))
Alfa = float(input("Sudut Alfa :"))
Sinalfa = math.sin(math.radians(Alfa)) Cosalfa = math.cos(math.radians(Alfa))
T1 = (M1 * G * Sinalfa)-(M1 * G * Cosalfa * P)
T2 = T1 + (M2 * G * Sinalfa) - (M2 * G * Cosalfa * P)
T3 = T2 + (M3 * G * Sinalfa) - (M3 * G * Cosalfa * P)
T4 = M4 * G
print ("Nilai T1 :",T1)
print ("Nilai T2 :",T2)
print ("Nilai T3 :",T3)
print ("Nilai T4 :",T4)
Hasil
Massa 1 :12 Massa 2 :12 Massa 3 :12 Massa 4 :12 Koefisien Gesek :0.2 Sudut Alfa :30 Nilai T1 : 38.47029789329917 Nilai T2 : 76.94059578659834 Nilai T3 : 115.41089367989751 Nilai T4 : 117.72
No 2
Torsimesin =eval(input("Torsi Mesin (N/m) :"))
r = eval(input("Jari-Jari Ban (m) :"))
g = eval(input("Gravitasi (m/s^2) :"))
ro = 1.2
m = eval(input("Massa Mobil (Kg) :"))
P = eval(input("Koefisien Gesek :"))
N = m*g
Fgesek = N*P
Froda = Torsimesin/r
if Froda < Fgesek :
Kmh = eval(input(" Top Speed (Km/h) :"))
Vmaks = Kmh/3.6
Cd = eval(input("Drag Koefisien :"))
A = eval(input("Area (m^2):"))
ro = 1.2
Fdrag = Cd*A*ro*Vmaks**2/2
atotal = (Froda-Fdrag)/m
t = Vmaks/atotal
print ("Waktu (s) Saat mencapai Vmaks:",t)
if Froda > Fgesek :
print ("Mobil Ngepot")
Hasil
Torsi Mesin (N/m) : 1000 Jari-Jari Ban (m) :0.14 Gravitasi (m/s^2) :9.81 Massa Mobil :2000 Koefisien Gesek :0.5 Top Speed (Km/h) :200 Drag Koefisien :0.44 Area (m^2):5 Waktu (t) Saat mencapai Vmaks: 36.20689655172415
Tugas Video
Musahabah Diri
Soal No 1
Soal No 2
Tugas
x0 = 0 # t awal y = 0 # V awal h = 0.01 # Increment h = 0,01 angka ketelitian x = eval(input("Masukkan nilai t: ")) if 0 <= x < 6:
def dydx(x, y):
return (4 * x - 0.48 * y ** 2 ) # Persamaaan jika 10t
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0) / h) # untuk mengetahui jumlah iterasi yang akan dilakukan maka panjangnya harus dibagi dengan increment yang telah ditentukan (h=0,01)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 6: # Ketika x >= 6, sesuai dengan soal maka nilai F(t) konstan pada 30N
def dydx(x, y):
return ( 12 - 0.48 * y ** 2 ) # memasukkan nilai F(t) konstan pada 30N
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0) / h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else: # untuk nilai lainnya yaitu nilai t saat negatif
print("Mohon masukkan nilai t positif.")
Tugas: CFD (mobil)
Landasan Teori
Drag force merupakan gaya kebelakang yang mendorong mundur serta menekan kebawah dan drag force ini disebabkan karena gangguan aliran udara pada bodi kendaraan dan parallel dengan arah angin. Drag force adalah jumlah semua gaya eksternal dalam aliran fluida yang melawan arah gerak objek dan disebabkan oleh aliran turbulen di sekitar benda yang melawan gerak maju objek melalui fluida (gas atau cairan).
Drag force dapat dimanfaatkan menjadi salah satu cara yang efisien untuk meningkatkan kecepatan kendaraan serta menghemat penggunaan bahan bakar. Hal ini dapat terjadi karena jika koefisien drag semakin kecil, maka hambatan udara terhadap mobil semakin kecil, sehingga mobil dapat melaju dengan tenaga dari mesin yang lebih sedikit dan pada akhirnya akan mengurangi pemakaian atau konsumsi bahan bakar mesin mobil.
Secara teori, jika koefisien drag semakin berkurang, maka kecepatan akan semakin meningkat, sesuai dengan persamaan gaya drag yang di mana koefisien drag berbanding terbalik dengan kecepatan. Oleh karena itu, pengaruh tahanan udara yang paling besar terjadi ketika laju kendaraan pada kecepatan yang paling rendah.
Faktor yang sangat penting dalam menentukan kualitas simulasi CFD salah satunya adalah meshing atau griding. Meshing merupakan proses dikritisasi domain fluida yang kontinu yang menjadi domain komputasi yang diskrit sehingga dapat diselesaikan persamaan-persamaan didalamnya dan menghasilkan solusi.
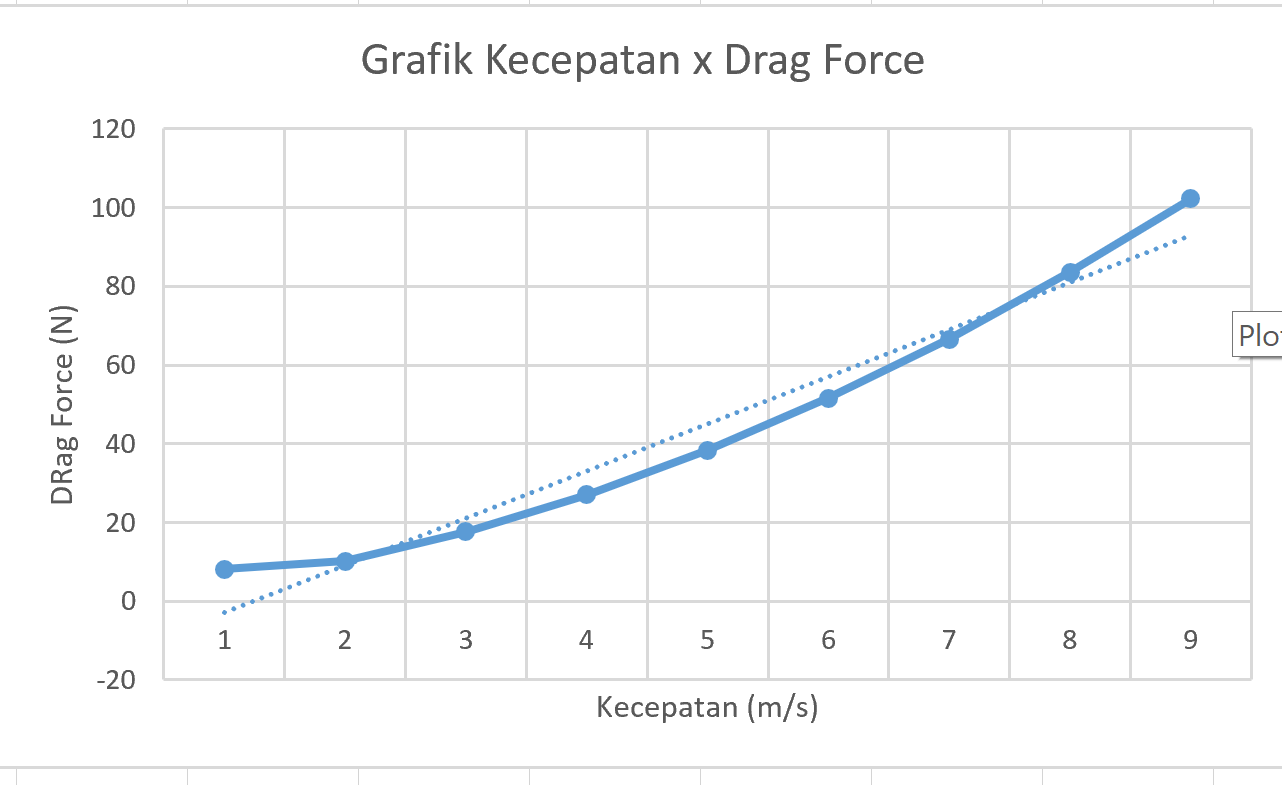
Setelah mengerti penggunaan CFDSOF-NG kami menghitung besarnya drag force dari mobil yang modelnya diberikan, dengan menggunakan aplikasi CFD. Kami mengikuti semua parameter yang telah di berikan mulai dari mesh yang ada sampai jenis aliran udara. Setelah dijalankan, berikut 10 data yang di dapatkan:
kecepatan drag force 10 8.11646 15 10.1848 20 17.6275 25 27.0084 30 38.3158 35 51.53 40 66.6329 45 83.5765 50 102.321
dengan grafik sebagai berikut:
TUGAS ANALISIS GAYA LIFT FORCE DAN DRAG FORCE PADA AIRFOIL (CFDSOF-NG)
Pada tugas kali ini, kita ditugaskan untuk menganalisis gaya yang terjadi pada sebuah airfoil (sayap pesawat). gaya yang telah dianalisis di hubungkan dengan percobaan sudut yang dibentuk airfoil dengan sumbu normal. Percobaan ini bertujuan untuk menentukan sudut maksimum untuk mendapatkan rasio gaya yang paling baik. Beriukut langkah langkah yang kami lakukan :
1. Mencari referensi airfoil lalu mendesign airfoil tersebut di inventor. 2. Setelah itu kita masukan kedalam CFDSOF-NG untuk di analisis. 3. Akan di dapat sebuah data yang nanti akan di plotting menjadi sebuah grafik. 4. mencari sebuah persamaan yang terbentuk. 5. melakukan optimasi mengunakan pemograman phyton. 6. menarik kesimpulan yang ada.
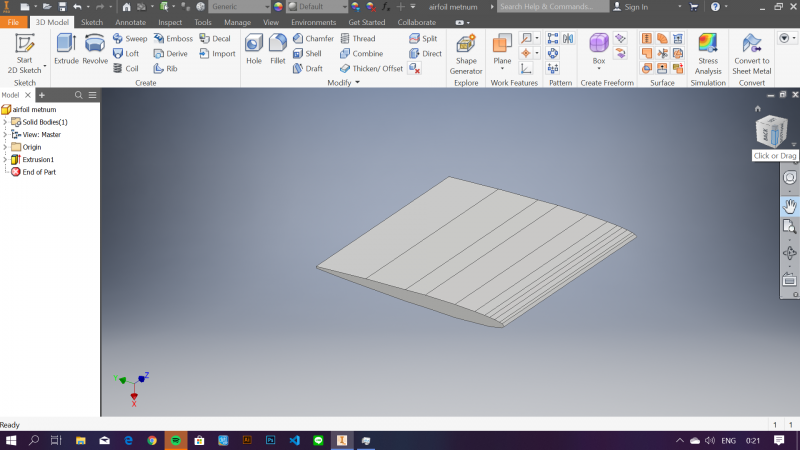
PEMBUATAN AIRFOIL
Berikut airfoil yang kelompok kami buat yang mendapatkan referensi dari NACA 0006.
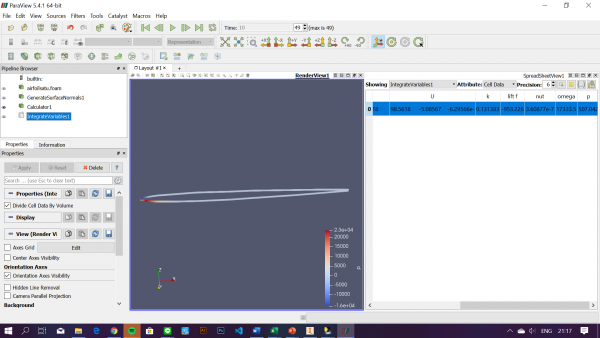
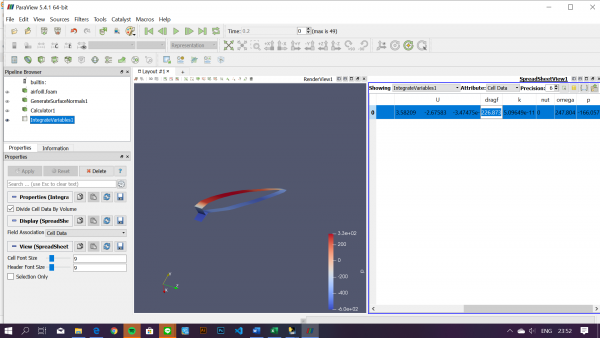
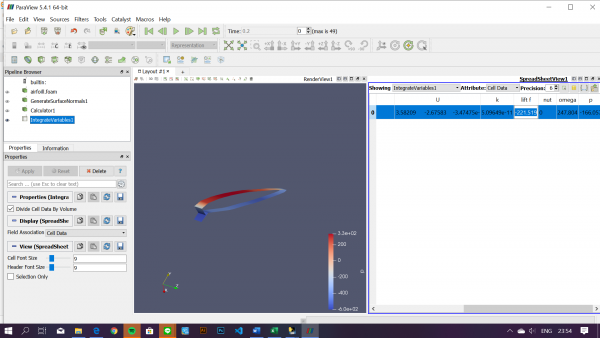
ANALISIS MENGGUNAKAN CFDSOF-NG
MENGOLAH DATA
Setelah melakukan analisis pada CFDSOF-NG, didapatkan data ytang berupa drag forve dan lift foce, berikut data yang telah kami dapatkan :
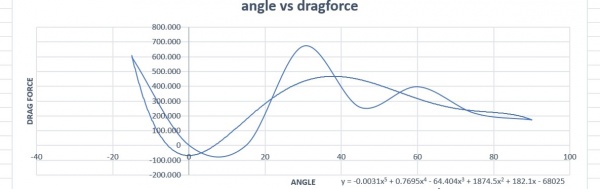
PEMBUATAN GRAFIK
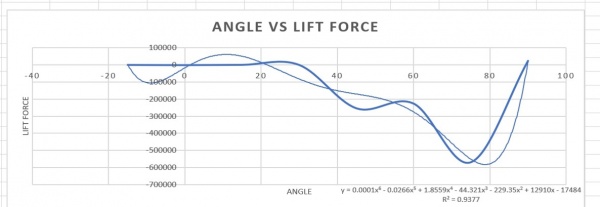
Setelah medapatkan data yang diinginkan, kita dapat memasukan data tersebut kedalam microsoft excel yang dimana nanti akan dibuat sebuah grafik yang menggunakan trend line guna mendapatkan persamaannya. berikut hasil grafik drag dan lift force terhadap sudut yang telah kami buat :
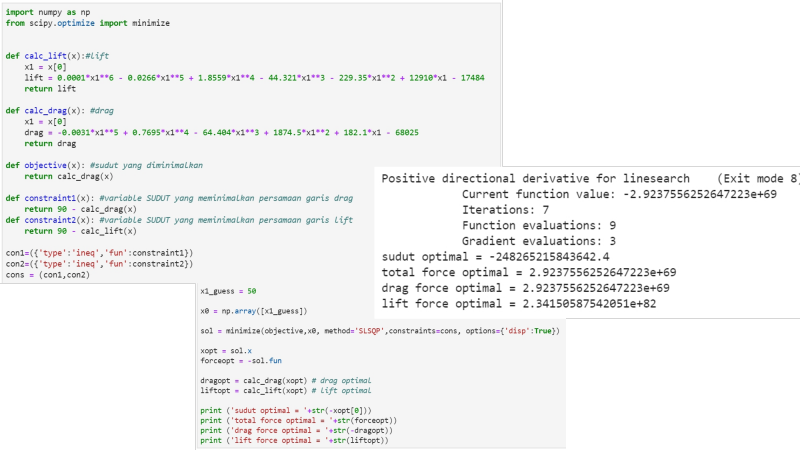
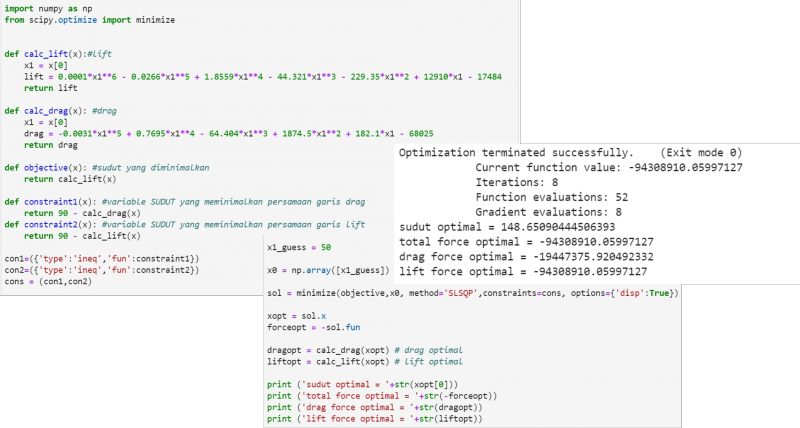
PEMOGRAMAN MENGGUNAKAN PHYTON
Setelah mendapatkan persamaan yang ada pada grafik, kita dapat membuat pemograman untuk melakukan optimasi, berikut optimasinya :
ANN
Artificial Neural Network Artificial (ANN) atau Jaringan Syaraf Tiruan merupakan sebuah teknik atau pendekatan pengolahan informasi yang terinspirasi oleh cara kerja sistem saraf biologis, khususnya pada sel otak manusia dalam memproses informasi. Elemen kunci dari teknik ini adalah struktur sistem pengolahan informasi yang bersifat unik dan beragam untuk tiap aplikasi. Neural Network terdiri dari sejumlah besar elemen pemrosesan informasi (neuron) yang saling terhubung dan bekerja bersama-sama untuk menyelesaikan sebuah masalah tertentu, yang pada umumnya dalah masalah klasifikasi ataupun prediksi.





Enable comment auto-refresher
RyansonJ
Permalink |
Muhammad.syariifi
Permalink |
Anonymous user #1
Permalink |
Anonymous user #1
Permalink |