Latihan Frame3DD padaTruss 2D DanyHP
Bismillah,
Tugas Mempelajari dan Prakter Program Frame3DD dengan kasus Truss 2D
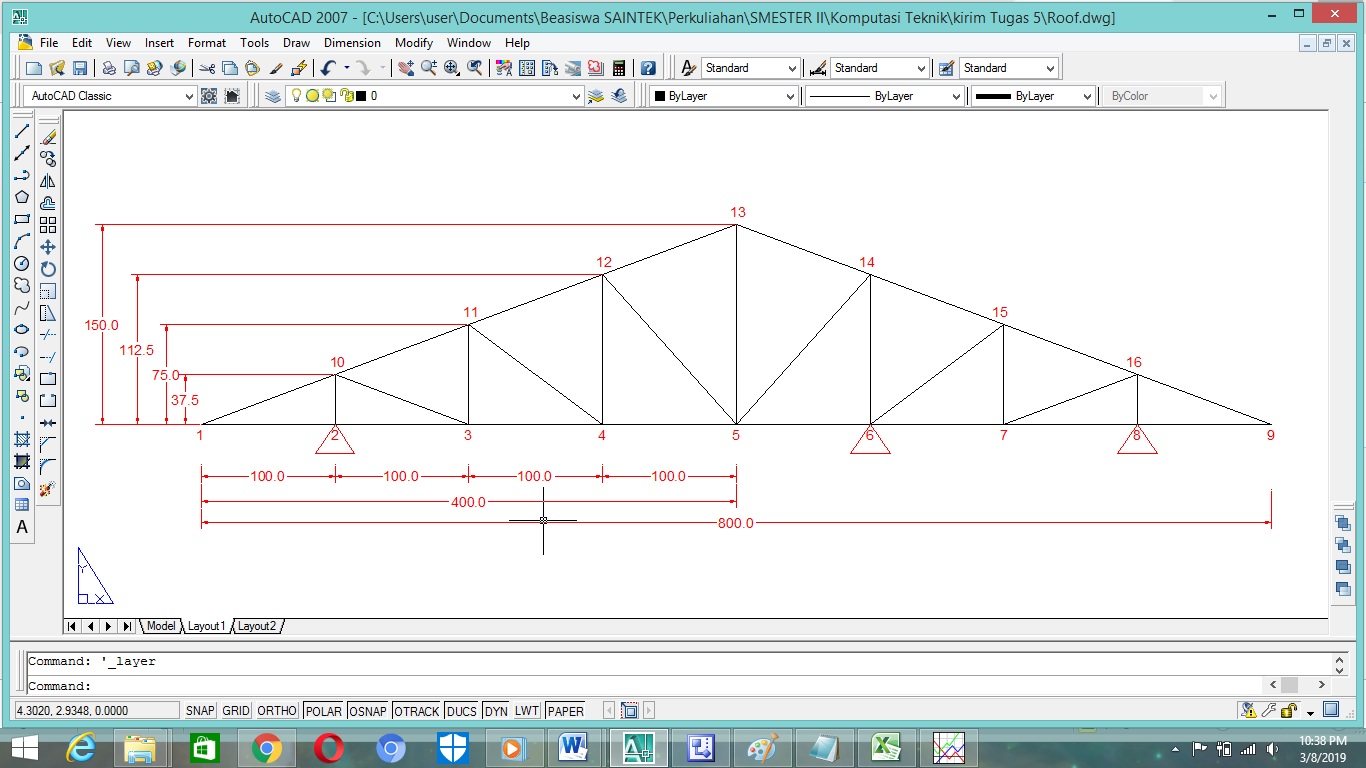
Rencana awal Struktur seperti gambar berikut :
Dengan input pada Frame3DD sebagai berikut :
Latihan Atap: linear static analysis of a 2D truss with support settlement (N,cm, ton) # node data ... 16 # number of nodes #.node x y z r units: cm 1 0 0 0 0 2 100 0 0 0 3 200 0 0 0 4 300 0 0 0 5 400 0 0 0 6 500 0 0 0 7 600 0 0 0 8 700 0 0 0 9 800 0 0 0 10 100 37.5 0 0 11 200 75 0 0 12 300 112.5 0 0 13 400 150 0 0 14 500 112.5 0 0 15 600 75 0 0 16 700 37.5 0 0 # reaction data ... 16 # number of nodes with reactions #.n x y z xx yy zz 1=fixed, 0= free 1 0 0 1 1 1 0 2 0 1 1 1 1 0 3 0 0 1 1 1 0 4 0 0 1 1 1 0 5 0 0 1 1 1 0 6 0 1 1 1 1 0 7 0 1 1 1 1 0 8 0 0 1 1 1 0 9 0 0 1 1 1 0 10 0 0 1 1 1 0 11 0 0 1 1 1 0 12 0 0 1 1 1 0 13 0 0 1 1 1 0 14 0 0 1 1 1 0 15 0 0 1 1 1 0 16 0 0 1 1 1 0 # frame element data ... 29 # number of frame elements #e n1 n2 Ax Asy Asz Jxx Iyy Izz E G roll density #. . . cm^2 cm^2 cm^2 cm^4 cm^4 cm^4 Mpa Mpa deg T/cm^3 1 1 2 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 2 2 3 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 3 3 4 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 4 4 5 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 5 5 6 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 6 6 7 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 7 7 8 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 8 8 9 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 9 2 10 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 10 3 11 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 11 4 12 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 12 5 13 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 13 6 14 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 14 7 15 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 15 8 16 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 16 3 10 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 17 4 11 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 18 5 12 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 19 5 14 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 20 6 15 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 21 7 16 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 22 1 10 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 23 10 11 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 24 11 12 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 25 12 13 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 26 13 14 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 27 14 15 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 28 15 16 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 29 16 9 10 1 1 1 1 0.01 210000 80000 0 7.85E-06 0 # 1: include shear deformations, 0: don't 0 # 1: include geometric stiffness, 0: don't include geometric stiffness 10 # exaggerate mesh deformations 1 # zoom scale for 3D plotting 10 # x-axis increment for internal forces 1 # number of static load cases # Begin Static Load Case 1 of 1 # gravitational acceleration for self-weight loading (global) # gX gY gZ # cm./s^2 cm./s^2 cm./s^2 0 0 0 7 # number of loaded nodes #.n Fx Fy Fz Mxx Myy Mzz # N N N N.cm N.cm N.cm 10 0 -2000 0 0 0 0 11 0 -2000 0 0 0 0 12 0 -2000 0 0 0 0 13 0 -2000 0 0 0 0 14 0 -2000 0 0 0 0 15 0 -2000 0 0 0 0 16 0 -2000 0 0 0 0 0 # number of uniform loads 0 # number of trapezoidal loads 0 # number of internal concentrated loads 0 # number of temperature loads 0 # number of nodes with prescribed displacements #.n Dx Dy Dz Dxx Dyy Dzz #. cm cm cm rad. rad. rad. 0 0 0 0 0 0 0 # End Static Load Case 1 of 1 # End of input data file for Latihan Atap
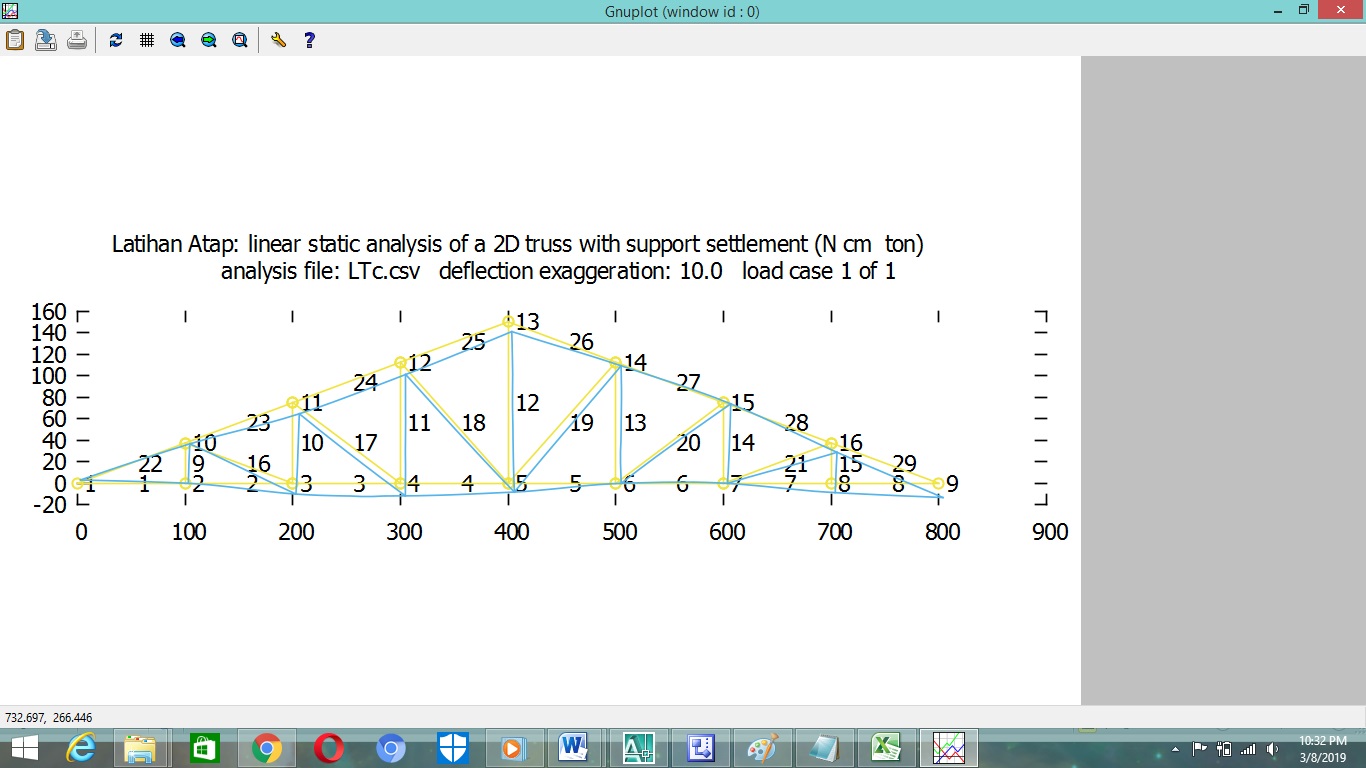
GNUPlot hasil running Frame3DD sebagai berikut :
Output Frame3DD terhadap input adalah sebagai berikut :
Frame3DD version: 20140514+ http://frame3dd.sf.net/ GPL Copyright (C) 1992-2015, Henri P. Gavin Frame3DD is distributed in the hope that it will be useful but with no warranty. For details see the GNU Public Licence: http://www.fsf.org/copyleft/gpl.html Latihan Atap: linear static analysis of a 2D truss with support settlement (N cm ton) Fri Mar 08 22:32:18 2019 In 2D problems the Y-axis is vertical. In 3D problems the Z-axis is vertical. ________________________________________________________________________________ 16 NODES 16 FIXED NODES 29 FRAME ELEMENTS 1 LOAD CASES ________________________________________________________________________________ N O D E D A T A R E S T R A I N T S Node X Y Z radius Fx Fy Fz Mx My Mz 1 0.000000 0.000000 0.000000 0.000 0 0 1 1 1 0 2 100.000000 0.000000 0.000000 0.000 0 1 1 1 1 0 3 200.000000 0.000000 0.000000 0.000 0 0 1 1 1 0 4 300.000000 0.000000 0.000000 0.000 0 0 1 1 1 0 5 400.000000 0.000000 0.000000 0.000 0 0 1 1 1 0 6 500.000000 0.000000 0.000000 0.000 0 1 1 1 1 0 7 600.000000 0.000000 0.000000 0.000 0 1 1 1 1 0 8 700.000000 0.000000 0.000000 0.000 0 0 1 1 1 0 9 800.000000 0.000000 0.000000 0.000 0 0 1 1 1 0 10 100.000000 37.500000 0.000000 0.000 0 0 1 1 1 0 11 200.000000 75.000000 0.000000 0.000 0 0 1 1 1 0 12 300.000000 112.500000 0.000000 0.000 0 0 1 1 1 0 13 400.000000 150.000000 0.000000 0.000 0 0 1 1 1 0 14 500.000000 112.500000 0.000000 0.000 0 0 1 1 1 0 15 600.000000 75.000000 0.000000 0.000 0 0 1 1 1 0 16 700.000000 37.500000 0.000000 0.000 0 0 1 1 1 0 F R A M E E L E M E N T D A T A (local) Elmnt J1 J2 Ax Asy Asz Jxx Iyy Izz E G roll density 1 1 2 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 2 2 3 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 3 3 4 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 4 4 5 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 5 5 6 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 6 6 7 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 7 7 8 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 8 8 9 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 9 2 10 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 10 3 11 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 11 4 12 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 12 5 13 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 13 6 14 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 14 7 15 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 15 8 16 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 16 3 10 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 17 4 11 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 18 5 12 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 19 5 14 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 20 6 15 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 21 7 16 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 22 1 10 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 23 10 11 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 24 11 12 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 25 12 13 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 26 13 14 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 27 14 15 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 28 15 16 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 29 16 9 10.0 1.0 1.0 1.0 1.0 0.0 210000.0 80000.0 0 7.85e-006 Neglect shear deformations. Neglect geometric stiffness. L O A D C A S E 1 O F 1 ... Gravity X = 0.0 Gravity Y = 0.0 Gravity Z = 0.0 7 concentrated loads 0 uniformly distributed loads 0 trapezoidally distributed loads 0 concentrated point loads 0 temperature loads 0 prescribed displacements N O D A L L O A D S + E Q U I V A L E N T N O D A L L O A D S (global) Node Fx Fy Fz Mxx Myy Mzz 10 0.000 -2000.000 0.000 0.000 0.000 0.000 11 0.000 -2000.000 0.000 0.000 0.000 0.000 12 0.000 -2000.000 0.000 0.000 0.000 0.000 13 0.000 -2000.000 0.000 0.000 0.000 0.000 14 0.000 -2000.000 0.000 0.000 0.000 0.000 15 0.000 -2000.000 0.000 0.000 0.000 0.000 16 0.000 -2000.000 0.000 0.000 0.000 0.000 E L A S T I C S T I F F N E S S A N A L Y S I S via L D L' decomposition L O A D C A S E 1 O F 1 ... N O D E D I S P L A C E M E N T S (global) Node X-dsp Y-dsp Z-dsp X-rot Y-rot Z-rot 1 0.292386 0.313408 0.0 0.0 0.0 -0.002586 2 0.292386 0.0 0.0 0.0 0.0 -0.004830 3 0.292388 -0.993820 0.0 0.0 0.0 -0.007049 4 0.452187 -1.160484 0.0 0.0 0.0 0.000819 5 0.580597 -0.808159 0.0 0.0 0.0 0.004777 6 0.498793 0.0 0.0 0.0 0.0 0.002964 7 0.371809 0.0 0.0 0.0 0.0 -0.006179 8 0.371808 -0.863795 0.0 0.0 0.0 -0.005314 9 0.371808 -1.315090 0.0 0.0 0.0 -0.003963 10 0.440160 -0.080658 0.0 0.0 0.0 -0.006008 11 0.604784 -1.038763 0.0 0.0 0.0 -0.004121 12 0.484070 -1.133999 0.0 0.0 0.0 0.000807 13 0.334722 -0.895640 0.0 0.0 0.0 0.003753 14 0.487530 -0.328251 0.0 0.0 0.0 0.003109 15 0.669196 -0.109549 0.0 0.0 0.0 -0.002957 16 0.541044 -0.863795 0.0 0.0 0.0 -0.005930 F R A M E E L E M E N T E N D F O R C E S (local) Elmn