Tanveer khan

Hello! Welcome to my Wiki page.

I am Tanveer khan from Pakistan, studying at the Faculty of Engineering Universitas Indonesia(FTUI). My major is Mechanical engineering and my specialty is manufacturing and automation systems. I've enrolled in a Finite Element and Multiphysics course to gain a deeper understanding of the fundamental principles and applications of FEM, as well as to explore various types of simulations.

Task#01 (DAI5 Framework):

Hello, I am Tanveer Khan presenting the DAI5 Framework, an innovative approach developed by Dr. Ahmed Indra (DAI). This method, DAI5, focuses on intentions, initial thinking, idealizations, and instruction sets for effective problem-solving. I discuss the unique aspects of DAI5 and how it differs from traditional approaches, emphasizing the importance of clarity and specificity in instructions. Viewers are encouraged to understand the significance of setting clear objectives and simplifying complex problems.

Task#02 (Pipe stress analysis using Ansys 2021R2):

I used the following specifications for the stress analysis of the pipe using the Ansys 2021R2;

Material:

1)Structural steel.

Geometric dimensions:

1) Length: 200mm.

2) Outer Diameter: 50mm.

3) Inner Diameter: 45mm.

4) Thickness: 2.5mm.

Boundary conditions:

1) Fixed right end.

2) Applied load to the left end (Load= 50N).

alt text

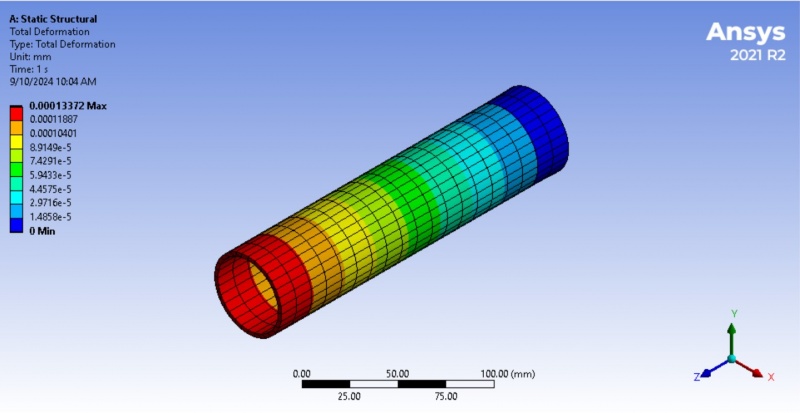
The image shows a structural analysis result from ANSYS software. The analysis focused on the total deformation of a pipe under 50 N load. The color gradient ranges from red (maximum deformation) to blue (minimum deformation). Red represents the area with the highest deformation, around 0.00013372 mm. Blue indicates the region with little or no deformation. Based on the image, the highest deformation occurs at the left end of the pipe, which is colored red, while the least deformation occurs at the opposite end, in blue which is 0 mm.

alt text

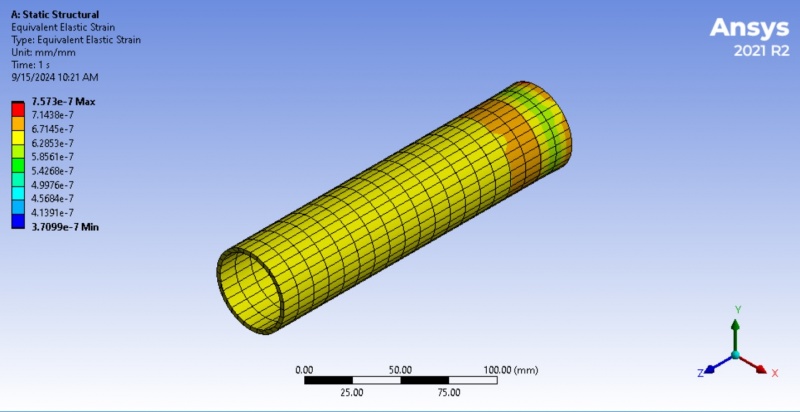
The image shows strain analysis results from an Ansys simulation, specifically for a pipe, analyzed using static structural analysis. The result shows the elastic strain distribution in a pipe under 50N load. The maximum strain occurs near the right end of the pipe, possibly due to concentrated stresses, while the rest of the pipe experiences a more uniform, lower strain. The color scale on the left ranges from blue (minimum strain value 3.7099×10^−7) to red (maximum strain value 7.573×10^−7). Blue/Cyan/Green: These colors represent regions experiencing low to moderate elastic strain. Yellow/Orange/Red: These regions experience higher elastic strain, with red indicating the maximum strain values. The highest elastic strain (indicated by red and orange) is located toward the right end of the pipe. This suggests that this portion is undergoing the most deformation under the applied load. On the other hand, the lowest strain (blue) is spread along the middle to the left side of the pipe. This indicates that these areas are relatively less affected by the applied loads, experiencing lower deformation.

alt text

The given image shows the result of a finite element analysis (FEA) of a pipe under static structural loading 50N, likely performed in Ansys 2021 R2. The analysis focuses on the Equivalent Stress, specifically the von Mises stress, which is used to predict the yielding of materials under complex loading conditions. The color bar on the left indicates the magnitude of von Mises stress in MPa (megapascals), ranging from 0.073522 MPa (blue) to 0.15051 MPa (red). The color distribution on the pipe shows the areas experiencing different stress levels. Red and yellow areas near the end of the pipe are experiencing the highest stress, while blue and green areas are under lower stress. The highest stress 0.15051 MPa occurs near the end of the pipe, where the colors transition from green to yellow and red. The rest of the pipe has lower stress values, predominantly in the orange-yellow range, indicating that most of the structure is experiencing moderate stress levels. Blue areas, especially on the opposite end, indicate the regions under minimal stress.

Basic questions:

Question(1): Is the force term internal or external in stress-force relation? >>(Sigma= F/A)?

Question(2): Does stress force direction dependent?

Question(3): How do we form the global stiffness matrix based on element-wise stiffness matrices?