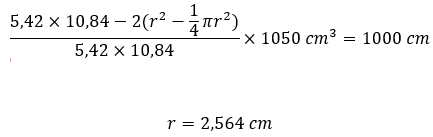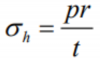Ihza Lathansa (Metnum)

Nama: Ihza Lathansa

NPM: 2106728143

Jurusan: Teknik Mesin

Tugas hydrogen storage Optimization

Hydrogen Storage Optimazation adalah proses meningkatkan metode dan teknologi yang digunakan untuk menyimpan hidrogen dengan efisien dan efektif. Hidrogen adalah pembawa energi yang serbaguna dan memiliki potensi untuk memainkan peran yang signifikan dalam sistem energi bersih dan berkelanjutan. Namun, salah satu tantangan dalam memanfaatkan hidrogen adalah kerapatan rendah dan energi per unit volume, yang membutuhkan teknik penyimpanan khusus.

To optimize hydrogen storage, you can follow these general steps:

1. Define the Objective: Clearly articulate the specific objective you want to achieve through the optimization process. For example, it could be to maximize storage capacity, minimize cost, optimize safety, or strike a balance between multiple factors.

2. Identify Variables and Constraints: Determine the key variables that affect the storage system's performance, such as storage volume, pressure, temperature, and cost. Also, consider any constraints that need to be satisfied, such as safety regulations, infrastructure limitations, or operational requirements.

3. Formulate a Mathematical Model: Develop a mathematical model that represents the relationship between the variables, constraints, and the objective function. The model should accurately capture the behavior of the hydrogen storage system and allow for efficient optimization.

4. Choose an Optimization Method: Select an appropriate optimization method based on the characteristics of the problem. Consider factors like the size and complexity of the search space, the presence of nonlinearities or discrete decisions, and the available computational resources. Genetic algorithms, simulated annealing, particle swarm optimization, and mathematical programming techniques like linear programming or nonlinear programming can be considered.

5. Implement the Optimization Algorithm: Translate the mathematical model and the chosen optimization method into a computer program. This program should take the model inputs, constraints, and objective function and use the optimization algorithm to find the optimal or near-optimal solution.

6. Perform Sensitivity Analysis: Analyze the sensitivity of the optimized solution to changes in key parameters. This analysis helps to understand how variations in variables or constraints affect the overall performance of the hydrogen storage system.

7. Validate and Refine: Validate the optimized solution by comparing it against real-world data or validated simulation models. If necessary, refine the model or optimization approach based on the insights gained during the validation process.

8. Iterate and Improve: Optimization is an iterative process, and it may be necessary to refine the model or adjust the objective and constraints based on feedback or new information. Continuously evaluate and improve the optimization results to achieve better performance.

9. Consider Practical Considerations: While optimizing the storage system, take into account practical considerations such as safety, regulatory requirements, infrastructure limitations, and environmental impacts. Ensure that the optimized solution is feasible and aligned with real-world constraints.

FINAL REPORT Optimization of Hydrogen Storage

1.Requirements : Designing hydrogen storage at 8 bar with a capacity of 1 liter and budget of Rp 500.000

2.Material Constrain

First of all, we need a material so I choose stainless steel Grade 304, because :

Corrosion Resistance: Stainless steel exhibits excellent corrosion resistance, which is crucial when storing hydrogen. Hydrogen gas can cause embrittlement and degradation in some materials, but stainless steel resists hydrogen-induced cracking and degradation, ensuring the integrity and safety of the storage system.

Strength and Durability: Stainless steel has high strength and durability, making it suitable for high-pressure applications. It can withstand the forces exerted by the stored hydrogen without deforming or failing, ensuring the structural integrity of the storage vessel.

Wide Availability: Stainless steel is widely available and commonly used in various industries. This availability contributes to a competitive market, making stainless steel a cost-effective option for hydrogen storage compared to some specialized or less commonly used materials.

below are the properties

3.Geometrical Constraint

Geometry Optimization's goal is to minimize the surface area of hydrogen storage in order to save material needs. The geometry could have many combinations of radius and height in order to achieve 1 liter size. Below are programming code to calculate the minimum surface area to achieve 1 liter volume

import numpy as np
from scipy.optimize import minimize

# Define the objective function
def objective(x):
    radius, height = x
    surface_area = 2 * np.pi * radius * (radius + height)
    return surface_area

# Define the volume constraint function
def volume_constraint(x):
    radius, height = x
    volume = np.pi * radius**2 * height
    return volume - 1000

# Define the optimization problem
x0 = [1.0, 10.0]
bounds = [(0, None), (0, None)]
constraint = {'type': 'eq', 'fun': volume_constraint}
problem = minimize(objective, x0, bounds=bounds, constraints=constraint)

# Extract the optimized results
optimized_radius = problem.x[0]
optimized_height = problem.x[1]
minimum_surface_area = problem.fun

# Print the optimized results
print("Optimal Geometry:")
print("Optimal Radius: cm", optimized_radius)
print("Optimal Height: cm", optimized_height)
print("Minimum Surface Area: cm", minimum_surface_area)

Berikut merupakan hasil perhitungan

4.End Cap Geometry Consideration

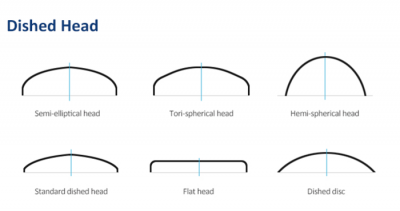
To minimize stress concentration at the corners of geometry, the torispherical end heads is a good alternatif. Torispherical heads are designed to withstand high internal or external pressures. The curved shape of the head helps distribute the pressure more evenly, reducing stress concentrations compared to flat or hemispherical heads. This design provides structural integrity and enhances the overall strength of the pressure vessel or tank. Torispherical heads offer good volume efficiency, meaning they provide a higher storage capacity within a given diameter compared to other head designs. The curved shape allows for a larger internal volume while maintaining a compact form factor. This can be particularly advantageous when space is limited, as it allows for more efficient use of available storage area.

However, the formation of these end caps certainly reduces the volume of the hydrogen tank. Therefore, the basic geometry of the tank is made with a larger volume as above, namely 1050 cm^3 so that the absorption volume due to these end caps does not fall below the 1 liter limit that has been set. The area is proportional to the volume so that comparison calculations can be carried out. Through this calculation, the radius of the fillet can be found.

The fillet radius obtained for the tank's end caps is 2,564 cm

5.Material Strength Constraint

In a pressurized storage system, the strength of the material and the plate thickness of the tank must be able to withstand the pressure of the gas pressing in all directions on the tank wall. In terms of specifications, this 1 liter hydrogen tank also has a pressure limit of 8 bar. The thickness of this tank plate can be calculated by the following hoop stress equation.

The size range of plate thickness should not be less than 1/5 of the tank radius. According to ASME BPV Code Section VIII D.1, the minimum tank plate thickness is 1/16 in or 1.59 mm without considering corrosion, material or dimensions.

Untuk mengetahui apakah material akan mengalami kegagalan pada ketebalan tertentu, Saya akan melakukan perhitungan Hoop Stress dengan menggunakan Iterasi

Code Iterasi

r = 5.42e-2
p = 800000
t = 2.9e-3

while t < 12e-3:
  hoop = (r * p)/(t)
  print('for thickness', t, 'hoop stress =', hoop, "Pa")
  t += 1e-3
  if hoop > 215e6:
    break

Kode yang diberikan menghitung tegangan hoop untuk berbagai nilai ketebalan mulai dari 2,9 mm hingga 12 mm

Berdasarkan hasil, semua nilai ketebalan mulai dari 2,9 mm hingga 12 mm dengan kenaikan 1 mm berada di bawah Yield Strength sehingga range ketebalan tersebut aman untuk digunakan.

6.Budget Constraint