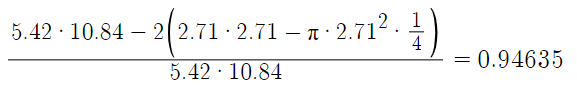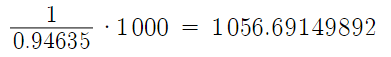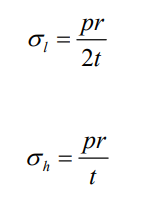M. Said Jiddan Walta
Contents
Introduction
Hello, my name is M. Said Jiddan Walta, commonly referred to as Jiddan. This page will be a platform for me to describe the results of my conscious learning and development during my short time in the Numerical Method class.
NPM: 2106718256
Major: Mechanical Engineering
E-mail: m.said11@ui.ac.id
I entered Mechanical Engineering fueled by a profound interest in ballistics and defense technology, and I hope to learn more about the foundations of mechanics and energy transfer that are the building blocks for understanding my field of interest.
Session Review
23 May 2023 Class
As an introductory class, our lecturer Dr. Ahmad Indra Siswantara introduced himself and his focus of study on the concept of consciousness, and invites us to participate in the discussion on the importance of applying consciousness in our daily lives as well as the recurrence of difficult concepts in the problems that we face that remind us to practice consciousness about the limitations of human understanding. Outside class time, a follow-up discussion was conducted in the class group for practicing consciousness by inviting discussion on the most realistic solution of a typical limit problem. We were invited to explore the notion of infinity and the limitations of computing involving values that are typically referred to as 'undefined'. Lastly, our project for the remainder of the semester was introduced.\
30 May 2023 Class
In todays class of Numerical Method, Pak DAI asked us to discuss the Hydrogen Tank Design and Optimization project within the class with every class member to gain better knowledge on developing our overall results. Throughout the class, the discussion was moderated by Patrick Samperuru as a replacement for the class coordinator, M. Jiddan Walta, who was at the time absent due to exchange matters. In this discussion, we started by making an outline on the project objective function which was to create a functional hydrogen tank design that is optimized following the constraint parameters of pressure at 8 bars, a capacity of 1 liter, and a maximum budget of 500,000 IDR. According to Benarido Amri, the ideal material for a high pressure cylinder has a very high tensile strength, a low density, and does not react with hydrogen or allow hydrogen to diffuse into it. Most pressure cylinders to date have used austenitic stainless steel. Patrick Samperuru then continued the discussion on the material by stating several potential materials that can be used based on the types of the hydrogen tanks, being type I of all metal, type II of metal with carbon fiber wrap, type III composite with metal lining, type IV composite with non-metal lining stating that type I and II is the most probable for the design. Next, M. Azkhariandra Aryaputra stated the importance of several design considerations such as storage tank design, safety measures, leakage mitigation, and material compatibility. Following the discussion of materials, Ariq Dhifan and Fadhlan Dindra added several materials that they want to use.
Next, we conversed the 3 main points needed in our optimization. This include the design variable, objective function, constraint which can be different for every class member. Patrick Samperuru started by explain that his objective function is to accommodate the use of hydrogen tanks in the field that is more complex and dynamic meaning it would need a constraint of a high strength and wear fatigue so that is can used for long term, which is achieved by choosing an all metal tank. For Vegantra Siaga, he wanted a pressure constraint because hydrogen storage systems often have pressure limits to ensure safe operation, where pressure constraints can be defined as upper and lower bounds on the hydrogen storage pressure that prevent the storage system from operating outside the desired pressure range. According to Faris Pasya, space and weight constraints can be used as well depending on the application, there may be limitations on the available space or weight of the pressurized hydrogen system. These constraints can influence the choice of tank size, material selection, and system layout. Next, M. Annawfal Rizky stated that he wants the constraint to be the compatibility with hydrogen, The tank material should be compatible with hydrogen gas to prevent any chemical reactions, embrittlement, or degradation that could affect the tank's performance or safety. Material selection is crucial to ensure compatibility and avoid hydrogen diffusion or leakage. For M. Ikhsan Rahadian, we chose safety due to the high pressure of hydrogen, and its highly flammable, the safety of the tank is very important. choosing the right material such as aluminum alloy 6061 can increase the strength and safety, and also choose the right design.
Numerical Method - Case Study of Pressurized Hydrogen Storage
Substance Study
For the Numerical Method class, we were tasked with a project on the design and optimization of a Pressurized Hydrogen Storage, with the constraint parameters being the gas pressurized at 8 bars and the required storage volume being 1 liters. Hydrogen as a gas is useful for many industrial purposes as well as an energy source for certain vehicles and industrial appliances, and is often stored by the hundreds of liters in large tanks.
Hydrogen in its frequently encountered diatomic form of H2 gas is the lightest gas in the universe and is generally unreactive, but is readily combustible in its gaseous form. As an ultra-light gas, hydrogen occupies a substantial volume under standard conditions of pressure, i.e. atmospheric pressure. In order to store and transport hydrogen efficiently, this volume must be significantly reduced. The general methods for improving hydrogen transport and storage efficiency is through high-pressure storage in the gaseous form, very low temperature storage in the liquid form, or hydride-based storage in the solid form, though the most common being the first two. Having the highest yield of hydrogen in a fixed container volume requires pressurization up to 700 bars or more, which requires large amounts of energy and strong container design. Liquid hydrogen is cryogenic in nature, and therefore needs to be stored in extremely low temperatures to keep it in its liquid state, or at least to keep a majority of it from evaporating. For the case that we are assigned, the required storage amount is small and the pressure is also constrained, therefore the focus is not the efficiency of hydrogen yield being stored but instead the cost and material effectiveness of the container.
For the purpose of this project, it is important to begin designing the product with understanding the substance that it is meant to store, in this case hydrogen pressurized at 8 bars.
In its gaseous form at 8 bars of pressure and local indoor temperature in Indonesia being around 30 degrees Celsius, hydrogen gas has a density of 0.627 kilograms per cubic meter, which results in 1 liter or 0.001 cubic meters of the gas weighing 0.627 grams or less than 0.001 kg. This means that storing the gas at these conditions will only require a container material and design that can withstand wall pressure of 8 bars, while ideally having lower density such that the total weight of the container far exceeds the weight of the gas being stored.
Material Choice
Our goal in this case is to select a suitable material for the storage tank, with our priorities being focused on fulfilling the load requirements presented by the hydrogen in a safe manner, low weight, and cost-effectiveness. Safety is of great importance when designing hydrogen storage. The material used must possess high strength, resistance to fracture, and be capable of withstanding high pressures. Metals like steel and aluminum alloys are commonly employed due to their mechanical properties. However, special attention must be given to hydrogen embrittlement, a phenomenon that can cause material degradation and reduce safety. Thus, selecting materials with high resistance to hydrogen embrittlement, such as specific grades of steel, becomes crucial. Hydrogen has the smallest molecule size, which means it can permeate through certain materials over time. Permeation can lead to hydrogen loss, compromising the efficiency of the storage system and potentially raising safety concerns. Hence, selecting materials with low hydrogen permeability is important. Metals like steel and aluminum have relatively low permeability, especially when coated with appropriate barriers to minimize permeation. Composites, on the other hand, can have higher permeability, although this can be mitigated by employing diffusion barriers or modifying the polymer matrix.
On the topic of optimization of weight, composite materials, such as carbon fiber reinforced polymers (CFRP), offer an advantageous balance between strength and weight. CFRP has been commonly used for hydrogen storage tanks in certain regions, having the walls consist of a lightweight polymer matrix reinforced with carbon fibers, providing exceptional strength-to-weight ratios. These materials enable the construction of lightweight tanks. The cost of materials plays a significant role in the overall economics of hydrogen storage systems. Metals like steel are relatively affordable and widely available, making them cost-effective choices for bulk storage applications. However, advanced alloys with improved resistance to hydrogen embrittlement can be more expensive. In contrast, composite materials like CFRP have higher upfront costs due to their manufacturing processes.
With these factors in mind, the most likely choice is selecting a lighter grade of steel with mechanical properties that can supplement the requirements, with additional modifications and treatments to the material to further lower its hydrogen permeability.
Numerical Method - Design of Pressurized Hydrogen Storage
In the section below, I will proceed to implement knowledge I have learned in Numerical Methods class as well as prior classes in order to determine the most suitable optimized design for the hydrogen storage based on constraints and optimizing objective functions, with the focus being on optimization based on: a) geometrical constraints, b) strength constraints, and c) cost constraints.
Based on our class discussions, I have decided to select AISI 316 austenitic stainless steel as the material for its balance in availability in the public domain, strength and durability, machinability and malleability for manufacture, as well as compatibility with hydrogen permeability reduction treatments. Austenitic stainless steels have also been the one of the main selections for materials used in industrial hydrogen storage manufacture.
Geometrical Constraint
Base Geometry
One of the main components of designing the pressurized hydrogen storage is the measurements and geometry of the storage. Through our discussions in class and individual case studies, students in our class collectively agreed that the ideal shape of the storage is a cylindrical shape akin to those generally utilized by the industry. The parameters of the cylindrical shape however still needs to be found out using the methods that we have learned over the entire course of Numerical Method class.
The goals of the optimization process of this hydrogen storage as mentioned above in the case study section is to create a pressurized hydrogen storage that fulfills the requirements while remaining cost-effective. One of the main contributors to cost of production is the amount of material being used, which in the case of a cylindrical container, equal to the surface area of the product. The lower the total surface area of the product, the lower the total effective material that is required to craft it. For our case, the surface area needs to be minimized while maintaining a constraint of volume being equal to 1 liter or 1000 cubic centimeters. The radius and height of a cylinder that fulfills both qualities can be obtained using a simple optimization function that can be numerically computed using suitable code made in Python or MATLAB. For the purpose of this project, I utilized Python to create a code that manually computes the radius and height of a cylinder of 1000 centimeter cubic volume. There are other libraries such as SciPy that has compiled code for optimization into a singular function, but for the purpose of learning the following code is done manually.
Objective: Minimize surface area of cylindrical structure
Constraint: Internal volume of cylindrical structure must be equal to 1000 cubic centimeters (1 liter)
The first section of the code is to obtain a general range of radius values where the surface area is minimum, shown below:
from math import pi
import pprint
'''
r = radius
circle_area = pi * r**2
circle_circumference = 2 * pi * r
h = height
cylinder_volume = pi * r**2 * h
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * h)
constraint for cylinder_volume be a constant of 1 liter (cubic centimeter)
cylinder_volume = 1000
h in terms of r
h = 1000/(pi * r**2)
substitute in
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
'''
mylist = [] # create a list of (surface area, radius)
for r in range(1, 21): # assume a maximum of 20cm radius
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
mylist.append((cylinder_surface, r))
# test
pprint.pprint(mylist)The code above displays iterations from radius of 1 cm to 20 cm and their corresponding surface area values. By inspection, we can see that the minimum surface area occurs in the region between radius of 5 and 6 cm. For precision, we continue the code with a looping function to obtain the precise point where the minimum surface area occurs, and continue with computing the height for verification.
# once we find the range where area is minimum
# we can increment in smaller steps for precision
r = 5
surface_list = []
while True:
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
surface_list.append((cylinder_surface, r))
r += 0.01
if r > 6:
break
print('minimum surface area and radius: ', min(surface_list))
min_surface = min(surface_list)[0]
sf = "Minimum surface of a 1000ml tank = {:0.2f} square centimeters"
print(sf.format(min_surface))
radius = min(surface_list)[1]
print("Radius of 1000ml tank = {:0.2f} centimeters".format(radius))
height = 1000/(pi * radius**2)
print("Height of 1000ml tank = {:0.2f} centimeters".format(height))
sf = "Ratio of height to radius of a minimized surface can = {:0.2f}"
print(sf.format(height/radius))
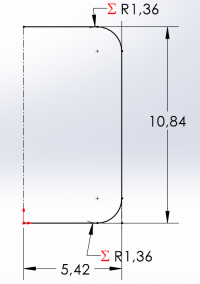
The result obtained by the code is shown on the right, where the suggested geometry for a cylindrical tank for 1 liter volume should maintain a 2:1 height to radius ratio with the radius being 5.42 cm, and the height at 10.84 cm consequently.
End Cap Compensation
Using a purely cylindrical geometry for the storage tank is likely to be dangerous due to the existence of the corners on the ends, which present stress concentration regions or sites of failure. Most pressure vessels take on a curved shape on their ends to reduce stress concentration by using three geometries: hemispherical, ellipsoidal, and torispherical. Highest volume and surface area addition to lowest addition also goes in the same order. Therefore, since our goal is to minimize surface area while maintaining the same volume, it is most efficient to take on a torispherical end cap shape. The torispherical shape can be simplified as the cylindrical shape that has been given partial filleting. This filleting adjustment will reduce the overall volume of the structure, however. Therefore we need to adjust the geometrical parameters to compensate for the reduction from the filleting to create the end cap.
We can set a fillet of radius equal to half the radius of the container to create a smooth curvature for greater stress concentration reduction. An example sketch has been made via a computer-aided design program to visualize the reduction in cross-sectional area from the circumferential face. By law of proportionality, a percentage reduction in the cross sectional area would be equal to the same reduction in volume, therefore we can calculate the percentage reduction and apply inversely to our required volume to obtained the new increased volume constraint.
As shown, assuming a fillet radius of half the container radius, we have a new volume constraint of 1056.69 cubic centimeters to account for the percentage reduction in volume following formation of torispherical end caps through filleting. We can repeat the iteration process that was previously used to obtain new radius and height values for the cylinder. Upon iterating the first section of code, we find that the minimum surface area occurs between values of 5 and 6 cm radii again, therefore the upper and lower bounds of the second set of code do not need to be adjusted. The final results as as follows:
minimum surface area and radius: (574.3098652360588, 5.519999999999989)
Minimum surface of a 1056.69ml tank = 574.31 square centimeters
Radius of 1056.69ml tank = 5.52 centimeters
Height of 1056.69ml tank = 10.45 centimeters
Ratio of height to radius of a minimized surface can = 1.89Strength Constraint
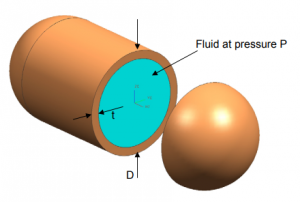
In a pressurized container environment, the most important requirement is that the container material's thickness and strength should be able to withstand the pressure exerted on the walls. Assuming an ideal situation where gaseous movement inside the container is uniform and steady, therefore of equal velocity at every point in space and time, we can assume the internal walls of the container experienced constant static stress equal to the pressure of the gas in the normal direction at every point. In this case, we can disregard the effects of shear stress or bending moments that might be present as theoretically the normal/axial stress presented by the pressure would be the most significant. These kind of assumptions can be grouped into a single assumption where we assume the container to be a thin-walled pressure vessel.
The constraints for this assumption to be true is that the radius must be at least 5 times the wall thickness, which we will verify later. The stresses that exist within a thin-wall cylindrical component are circumferential (hoop) stress and longitudinal stress. Radial stress also exists but can be neglected due to the radius being much greater than the wall thickness. Hoop stress and longitudinal stress can be obtained via the following formulae:
where p is the gage pressure of the fluid and t is the wall thickness.
Since the hoop stress is equal to twice the longitudinal stress, we can set it as the objective function over the latter since quantitatively failure will occur earlier due to the hoop stress instead of the longitudinal stress. Since we have already calculated the container radius previously, have the pressure constraint set at 8 bars of gage pressure from the hydrogen, we can numerically iterate for the thickness of the vessel to obtain a range of values of hoop stresses. From there, we can select thicknesses with corresponding hoop stresses that do not exceed allowable stress of the material, in this case we arbitrarily set at 0.875 of the yield strength of the material. In containment purposes such as these, deformations in the container can already be considered failure or at least compromising for the storage facility, hence the consideration for setting the constraint at the yield strength.
Literary Parameters
The range of wall thickness that is applicable is also not arbitrary outside of remaining less than one-fifth of the vessel radius. ASME BPV Code Section VIII D.1 states that wall thickness should always be at least 1/16 in (1.59 mm), not considering corrosion allowance, material, or dimensions. Literary source "Analysis, Synthesis, and Design of Chemical Processes" gives heuristics for wall thickness for rigidity based on vessel diameter: 4 mm (0.25 in) for 1.07 m (42 in) diameter and less than 8.1mm (0.32 in) for 1.07-1.52 m (42-60 in) diameter, and 11.7 mm (0.38 mm) for more than 1.52 m (60 in) diameter (Turton et al., 2012). Taking a conservative approach of setting the minimum thickness to be in between 1.59mm and 4mm, thereby 2.8mm, we will begin the iteration of the thickness from 2.80mm up to 11.04mm at increments of 0.01mm for precision.
Based on data obtained from Ferrobend, a typical workpiece of AISI 316 stainless steel has the mechanical properties as shown. For the purpose of our testing, we will utilize both a conservative and less conservative method by setting our limit at the yield strength as well as the maximum tensile strength to signify failure.
Iteration Process
We can use a simple code to numerically iterate the possible thickness and hoop stress values:
r = 5.52e-2
p = 800000
t = 2.8e-3
while t < 11e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 0.1e-3
if hoop > 205e9:
breakFrom the above code we obtain hoop stress values for each iterated thickness values from 2.8 mm to 11 mm. A further constraint was placed in the final lines where the looping would stop if the total hoop stress exceeded the yield strength of the material (stainless steel AISI 316).
From the results, all possible thickness values from 2.8mm to 11mm on 0.1mm increments remain within the yield strength constraint, therefore are all applicable. Shown below are the results from the code for thickness range 4 mm to 7 mm, with hoop stress values ranging below 10 MPa, which is less than 5% of the yield strength limit.
for thickness 0.004099999999999999 hoop stress = 10770731.707317077 Pa
for thickness 0.004199999999999999 hoop stress = 10514285.714285716 Pa
for thickness 0.004299999999999999 hoop stress = 10269767.441860467 Pa
for thickness 0.004399999999999999 hoop stress = 10036363.636363639 Pa
for thickness 0.0045 hoop stress = 9813333.333333334 Pa
for thickness 0.0046 hoop stress = 9600000.0 Pa
for thickness 0.0047 hoop stress = 9395744.680851063 Pa
for thickness 0.0048000000000000004 hoop stress = 9200000.0 Pa
for thickness 0.004900000000000001 hoop stress = 9012244.897959182 Pa
for thickness 0.005000000000000001 hoop stress = 8831999.999999998 Pa
for thickness 0.005100000000000001 hoop stress = 8658823.529411763 Pa
for thickness 0.0052000000000000015 hoop stress = 8492307.69230769 Pa
for thickness 0.005300000000000002 hoop stress = 8332075.47169811 Pa
for thickness 0.005400000000000002 hoop stress = 8177777.777777774 Pa
for thickness 0.005500000000000002 hoop stress = 8029090.909090905 Pa
for thickness 0.0056000000000000025 hoop stress = 7885714.285714282 Pa
for thickness 0.005700000000000003 hoop stress = 7747368.421052628 Pa
for thickness 0.005800000000000003 hoop stress = 7613793.103448272 Pa
for thickness 0.005900000000000003 hoop stress = 7484745.76271186 Pa
for thickness 0.006000000000000004 hoop stress = 7359999.999999995 Pa
for thickness 0.006100000000000004 hoop stress = 7239344.262295078 Pa
for thickness 0.006200000000000004 hoop stress = 7122580.645161286 Pa
for thickness 0.006300000000000004 hoop stress = 7009523.809523805 Pa
for thickness 0.006400000000000005 hoop stress = 6899999.999999995 Pa
for thickness 0.006500000000000005 hoop stress = 6793846.153846148 Pa
for thickness 0.006600000000000005 hoop stress = 6690909.090909085 Pa
for thickness 0.006700000000000005 hoop stress = 6591044.776119398 Pa
for thickness 0.006800000000000006 hoop stress = 6494117.6470588185 Pa
for thickness 0.006900000000000006 hoop stress = 6399999.999999994 Pa
for thickness 0.007000000000000006 hoop stress = 6308571.428571423 PaCost Constraints
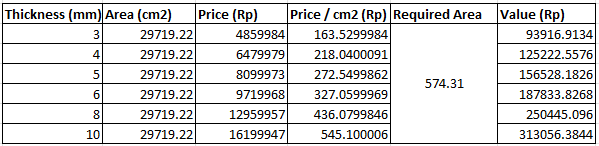
With the geometrical parameters available, we need to compare with the cost constraint that was provided which is that the total cost for materials used should not exceed Rp500.000,-. Therefore, from the material that has been previously considered, we must select the thickness which remain within the cost range. As this is a small-size thin-walled vessel, the most likely method of manufacture is through sheet-metal manufacturing like those used to manufacture storage and beverage cans. Therefore, material purchase would be done in the sheet-metal or plate form.