Tugas Besar Metode Numerik - Josiah Enrico S
Contents
Abstract
Introduction
Objective
- Membuat program analisis truss dan optimasi sederhana dengan Modelica
- Mengoptimasi harga pembuatan rangka truss sederhana dengan memvariasi dimensi dan elastisitas material.
Methodology
- Metode Optimasi Golden Section (univariabel)
- Metode Optimasi Golden Section (multivariabel)
Procedure
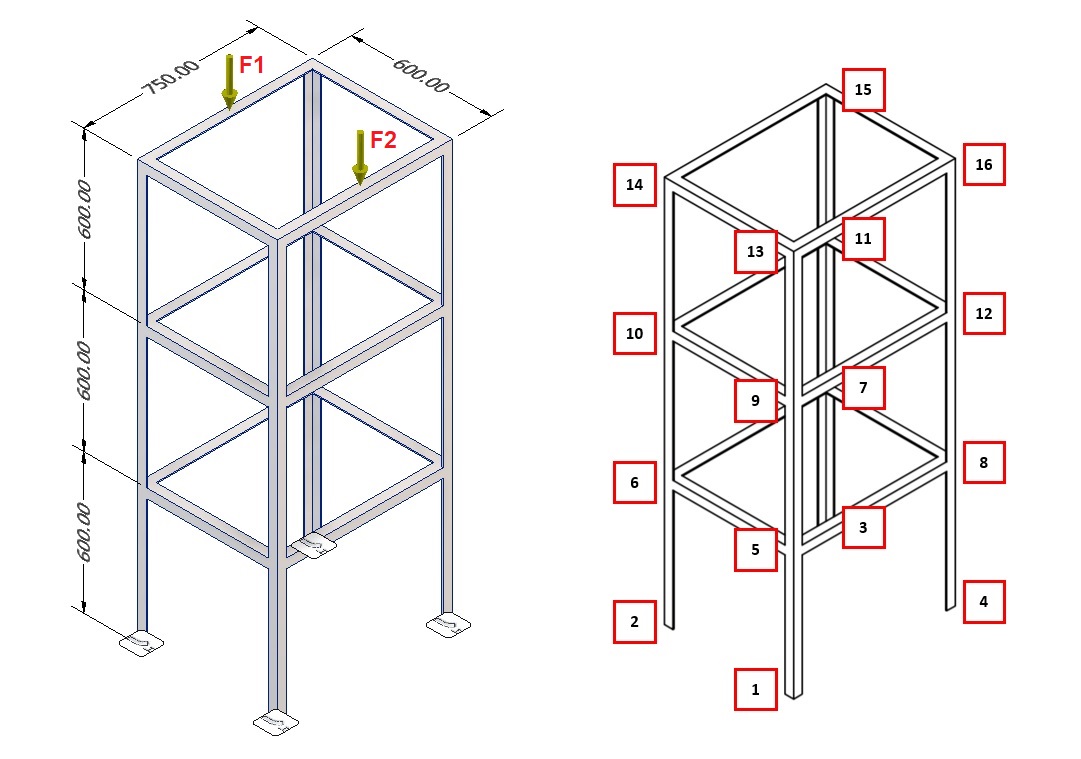
Geometri dan Load
| F1 | 2000 |
|---|---|
| F2 | 1000 |
Constraint:
- Spesifikasi L (Panjang) dan geometri rangka truss
- Gaya beban terhadap struktur (1000 N dan 2000 N)
Asumsi:
- Beban akan terdistribusi hanya pada point penghubung dan semua gaya yang dipengaruhi moment diamggap tidak ada karena sistem bersifat truss
Koleksi Data
Data Proceessing
model Truss_3D_Tugas_Besar_Safety
// Base Code by Josiah Enrico S. 1906356286
// Editing and Testing by Ahmad M. Fahmi 1806181836
// Commenting and Cleaning by Christopher S. Erwin 1806201056
// === DEFINITION PHASE ===
// Define the properties of the truss arrangement
parameter Integer Nodes = size(node_points,1); // Number of Nodes
parameter Integer Members = size(node_pairs,1); // Number of Members
// Define the properties of the truss material
parameter Real Yield = 215e6; // Yield Strength (Pa)
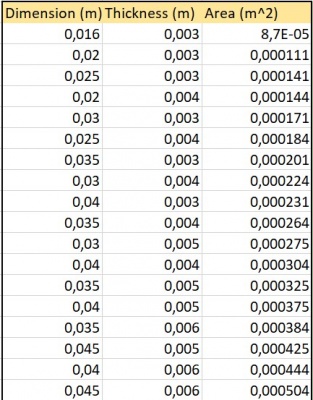
parameter Real Area = 0.000224; // Area L Profile [Dimension=0.03, Thickness=0,004] (m^2)
parameter Real Elas = 193e9; // Elasticity of material [SS 304] (Pa)
// Define connections; list pair of nodes joined by a member
parameter Integer node_pairs[:,2]=[1,5; 2,6; 3,7; 4,8; // Lowest vertical members
5,6; 6,7; 7,8; 5,8; // 1st shelf
5,9; 6,10; 7,11; 8,12; // Middle vertical members
9,10; 10,11; 11,12; 9,12; // 2nd shelf
9,13; 10,14; 11,15; 12,16; // Top vertical members
13,14; 14,15; 15,16; 13,16];// 3rd shelf
// Define coordinates and boundaries of each node
// [x, y, z, boundary_x, boundary_y, boundary_z]
// If the node is bound (stationary) along that axis, then boundary_axis = 1
// otherwise the node is free and boundary_axis = 0
parameter Real node_points[:,6]=[0.3,-0.375,0,1,1,1; // Node 1
-0.3,-0.375,0,1,1,1; // Node 2
-0.3,0.375,0,1,1,1; // Node 3
0.3,0.375,0,1,1,1; // Node 4
0.3,-0.375,0.6,0,0,0; // Node 5
-0.3,-0.375,0.6,0,0,0; // Node 6
-0.3,0.375,0.6,0,0,0; // Node 7
0.3,0.375,0.6,0,0,0; // Node 8
0.3,-0.375,1.2,0,0,0; // Node 9
-0.3,-0.375,1.2,0,0,0; // Node 10
-0.3,0.375,1.2,0,0,0; // Node 11
0.3,0.375,1.2,0,0,0; // Node 12
0.3,-0.375,1.8,0,0,0; // Node 13
-0.3,-0.375,1.8,0,0,0; // Node 14
-0.3,0.375,1.8,0,0,0; // Node 15
0.3,0.375,1.8,0,0,0]; // Node 16
// Define external forces in Newtons on each node
// [Fx, Fy, Fz]
parameter Real Forces[nodes_xyz]={0,0,0, // Node 1
0,0,0, // Node 2
0,0,0, // Node 3
0,0,0, // Node 4
0,0,0, // Node 5
0,0,0, // Node 6
0,0,0, // Node 7
0,0,0, // Node 8
0,0,0, // Node 9
0,0,0, // Node 10
0,0,0, // Node 11
0,0,0, // Node 12
0,0,-500, // Node 13
0,0,-1000, // Node 14
0,0,-1000, // Node 15
0,0,-500}; // Node 16
// === SOLUTION PHASE ===
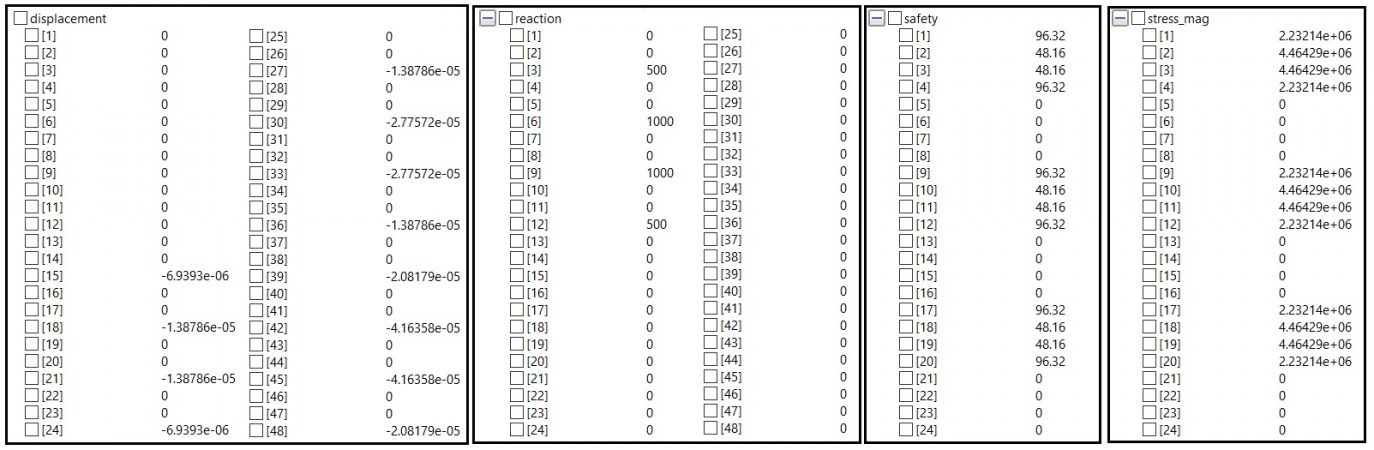
Real displacement[nodes_xyz], reaction[nodes_xyz];
Real check[3]; // To check if forces in xyz directions sum to zero (structure is static)
Real safety[Members]; // Safety Factor of each member (based on stress experienced)
Real mem_dis[3]; // Displacement in xyz directions experienced by member
Real stress_vector[3]; // Stress experienced by member in xyz directions
Real stress_mag[Members]; // Magnitude of stress experienced by member
protected
parameter Integer nodes_xyz = 3 * Nodes; // Size of vector of {node_#_x, node_#_y, node_#_z} containing all nodes
Real node_i[3], node_j[3]; // Coordinates in xyz for member's node pairs
// Global Stiffness Matrix construction
Real G_element[nodes_xyz, nodes_xyz], G_total[nodes_xyz, nodes_xyz], G_total_new[nodes_xyz, nodes_xyz];
// Transformation Matrix construction
Real cos_x, cos_y, cos_z, L, T[3,3];
// Limits to eliminate Float Errors
Real err_solve = 10e-10, err_check = 10e-4;
algorithm
//Creating Global Matrix
G_total := identity(nodes_xyz);
for mem in 1:Members loop
// Get coordinates of member's nodes
for i in 1:3 loop
node_i[i] := node_points[node_pairs[mem,1],i];
node_j[i] := node_points[node_pairs[mem,2],i];
end for;
// Finding the Stiffness Matrix [Ke]
// {F} = [Ke]{U}
// [Ke] = k[T]
L := Modelica.Math.Vectors.length(node_j - node_i);
cos_x := (node_j[1]-node_i[1])/L;
cos_y := (node_j[2]-node_i[2])/L;
cos_z := (node_j[3]-node_i[3])/L;
T := (Area * Elas / L)*[cos_x^2,cos_x*cos_y,cos_x*cos_z;
cos_y*cos_x,cos_y^2,cos_y*cos_z;
cos_z*cos_x,cos_z*cos_y,cos_z^2];
// Transforming to Global Matrix
G_element := zeros(nodes_xyz,nodes_xyz);
for m,n in 1:3 loop
G_element[3*(node_pairs[mem,1]-1)+m, 3*(node_pairs[mem,1]-1)+n] := T[m,n];
G_element[3*(node_pairs[mem,2]-1)+m, 3*(node_pairs[mem,2]-1)+n] := T[m,n];
G_element[3*(node_pairs[mem,2]-1)+m, 3*(node_pairs[mem,1]-1)+n] := -T[m,n];
G_element[3*(node_pairs[mem,1]-1)+m, 3*(node_pairs[mem,2]-1)+n] := -T[m,n];
end for;
// Adding to total Global Matrix
G_total_new := G_total + G_element;
G_total := G_total_new;
end for;
//Implementing boundary conditions to Global Matrix
for nod in 1:Nodes loop
// Boundary x-axis
if node_points[nod,4] <> 0 then
for i in 1:Nodes*3 loop
G_total[(nod*3)-2,i] := 0;
G_total[(nod*3)-2,(nod*3)-2] := 1;
end for;
end if;
// Boundary y-axis
if node_points[nod,5] <> 0 then
for i in 1:Nodes*3 loop
G_total[(nod*3)-1,i] := 0;
G_total[(nod*3)-1,(nod*3)-1] := 1;
end for;
end if;
// Boundary z-axis
if node_points[nod,6] <> 0 then
for i in 1:Nodes*3 loop
G_total[nod*3,i] := 0;
G_total[nod*3,nod*3] := 1;
end for;
end if;
end for;
// Solving displacement (U)
// [G_total]{U} = {F}
displacement := Modelica.Math.Matrices.solve(G_total, Forces);
// Solving reaction (R)
// {R} = [G_total]{U} - {F}
reaction := (G_total_new * displacement) - Forces;
// Eliminating float errors
for i in 1:nodes_xyz loop
reaction[i] := if abs(reaction[i])<= err_solve then 0 else reaction[i];
displacement[i] := if abs(displacement[i])<= err_solve then 0 else displacement[i];
end for;
// Checking Sum of Forces
// For static structures, should add up to 0
check[1]:=sum({reaction[i] for i in (1:3:(nodes_xyz-2))}) + sum({Forces[i] for i in (1:3:(nodes_xyz-2))});
check[2]:=sum({reaction[i] for i in (2:3:(nodes_xyz-1))}) + sum({Forces[i] for i in (2:3:(nodes_xyz-1))});
check[3]:=sum({reaction[i] for i in (3:3:(nodes_xyz))}) + sum({Forces[i] for i in (3:3:(nodes_xyz))});
// Eliminating float errors
for i in 1:3 loop
check[i] := if abs(check[i])<= err_check then 0 else check[i];
end for;
// === POSTPROCESSING PHASE ===
//Calculating stress in each truss
for mem in 1:Members loop
// Getting node coordinate data and displacement for current member
for i in 1:3 loop
node_i[i] := node_points[node_pairs[mem,1],i];
node_j[i] := node_points[node_pairs[mem,2],i];
mem_dis[i] := abs(displacement[3*(node_pairs[mem,1]-1)+i] - displacement[3*(node_pairs[mem,2]-1)+i]);
end for;
// Solving the Displacement Matrix for current member
// Stress = F/A = (E/L) * [dL]
L:=Modelica.Math.Vectors.length(node_j-node_i);
cos_x:=(node_j[1]- node_i[1])/L;
cos_y:=(node_j[2]- node_i[2])/L;
cos_z:=(node_j[3]- node_i[3])/L;
T := (Elas/L)*[cos_x^2,cos_x*cos_y,cos_x*cos_z;
cos_y*cos_x,cos_y^2,cos_y*cos_z;
cos_z*cos_x,cos_z*cos_y,cos_z^2];
stress_vector:=(T*mem_dis); // The stress in vector components {stress_x, stress_y, stress_z}
stress_mag[mem]:=Modelica.Math.Vectors.length(stress_vector); // Magnitude/length of the stress vectors for each member
end for;
// Safety Factor
// Factor of Safety = (Yield Strength of material) / (Stress experienced by Member)
for mem in 1:Members loop
if stress_mag[mem]>0 then
safety[mem] := Yield / stress_mag[mem];
else
safety[mem] := 0;
end if;
end for;
end Truss_3D_Tugas_Besar_Safety;
|
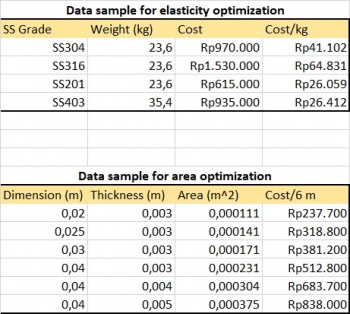
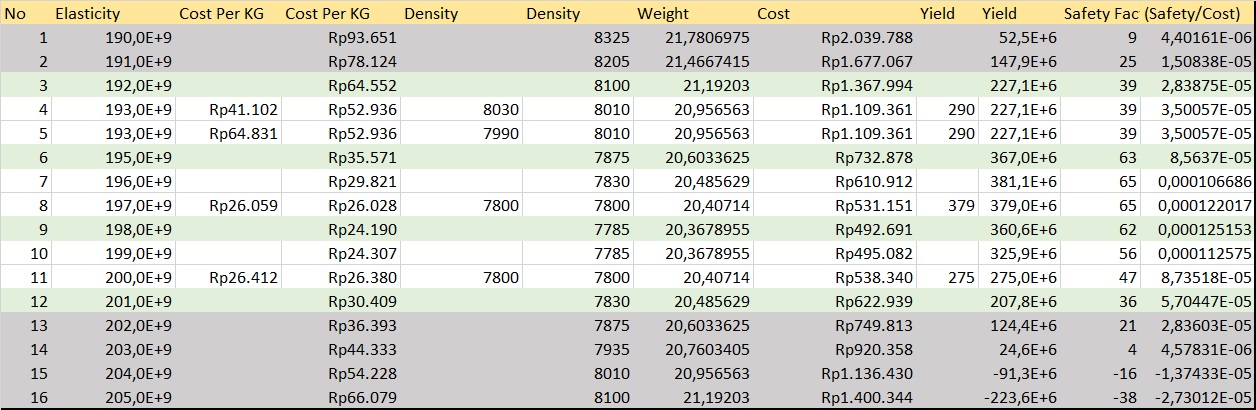
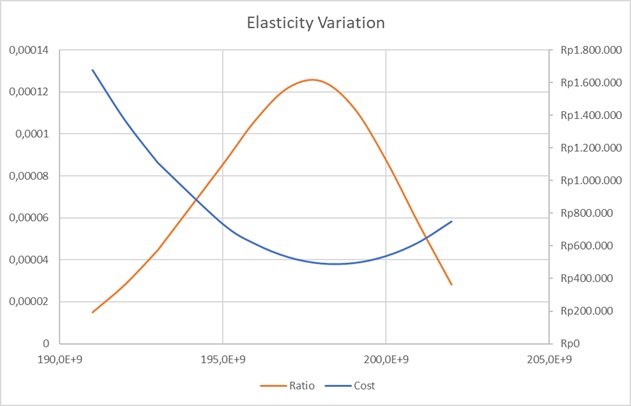
Elasticity Constraint
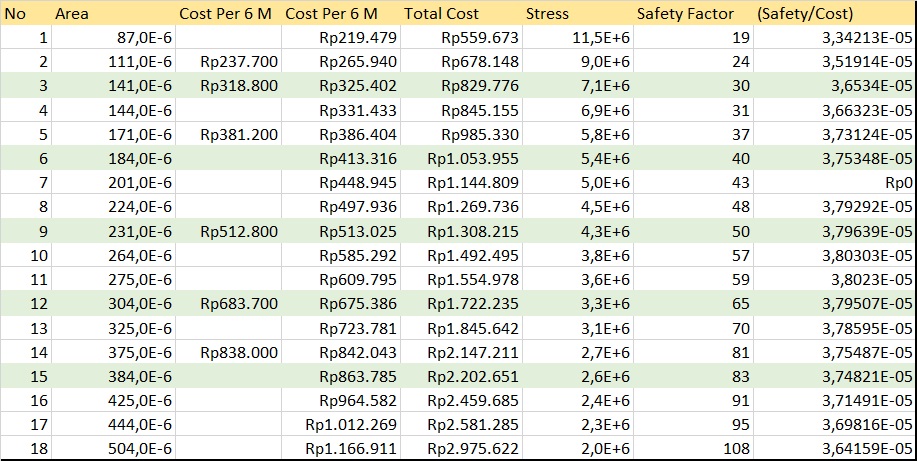
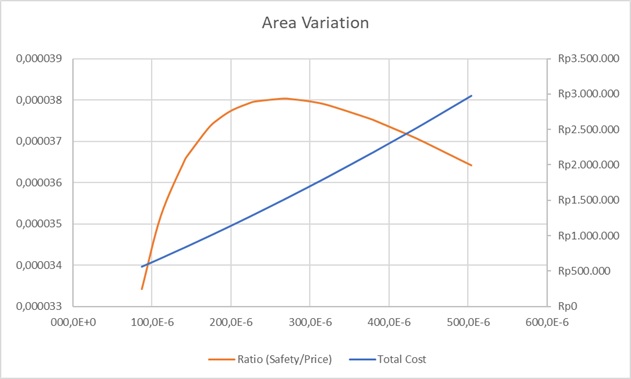
Area Constraint
Result and Analysis
|
Powell Method model Powell_Method_Opt_Jos_Ratio
parameter Integer order=2; //order of regression
parameter Integer GoldN=15; //maximum iteration of linear gold optimization
parameter Integer N=10; //maximum iteration
parameter Real maxerror=1e-50; //maximum error
//Assumed to be X function
parameter Real RatioArea[size(Area,1)]={3.6534e-5, 3.75348e-5, 3.79639e-5, 3.79507e-05, 3.74821e-05};
parameter Real CostArea[size(Area,1)]={829776,1053955,1308215,1722235,2202651};
parameter Real Area[:]={141e-6, 184e-6, 231e-6, 304e-6, 384e-6};
Real CoeArea[order+1];
Real CoeAreaCost[order+1];
//Assumed to be Y function
parameter Real RatioElas[size(Elas,1)]={2.83875e-5, 8.5637e-5, 12.5153e-5, 5.70447e-5};
parameter Real CostElas[size(Elas,1)]={1367994,732878,492691,622939};
parameter Real Elas[:]={192e9, 195e9, 198e9, 201e+9};
Real CoeElas[order+1];
Real CoeElasCost[order+1];
//Guessing Start (1 point, 2 vector) - the second vector will be auto-generated
parameter Real StartPoint[2]={171e-6,195e9};
parameter Real VectorPoint[2]={205e-6,200e9};
//Solution
Real RatioZ[N]; //Optimum result
Real CostZ; //Cost Optimum result
Real x3[2]; //Optimum point coordinate (x,y)
Real error[N]; //Error
protected
Real jos;
Real RatioZX;
Real RatioZY;
Real CostZX;
Real CostZY;
Real x0tes[2];
Real x0[2];
Real x1[2];
Real x2[2];
Real grad1;
Real grad2;
Real grad3;
//Checking approach
Real cek0[N];
Real cek1[N];
Real cek2[N];
Real cek3[N];
Real yek0[N];
Real yek1[N];
Real yek2[N];
Real yek3[N];
algorithm
//Creating function at both
CoeArea:=Curve_Fitting(Area,RatioArea,order);
CoeElas:=Curve_Fitting(Elas,RatioElas,order);
CoeAreaCost:=Curve_Fitting(Area,CostArea,order);
CoeElasCost:=Curve_Fitting(Elas,CostElas,order);
//Creating 2 vector defined in 2 gradient (grad1,grad2)
x0:=StartPoint;
x0tes:=VectorPoint;
grad1:=(x0tes[2]-x0[2])/(x0tes[1]-x0[1]);
grad2:=-0.5*grad1;
//Provide error variable
RatioZX:=CoeArea[1]*x0[1]^2+CoeArea[2]*x0[1]+CoeArea[3];
RatioZY:=CoeElas[1]*x0[2]^2+CoeElas[2]*x0[2]+CoeElas[3];
jos:=(RatioZX+RatioZY)/2;
//Computing approach
for i in 1:N loop
cek0[i]:=x0[1];
yek0[i]:=x0[2];
x1:=Gold_Opt_Func_2D_Vector(x0,grad1,GoldN,CoeArea,CoeElas);
cek1[i]:=x1[1];
yek1[i]:=x1[2];
x2:=Gold_Opt_Func_2D_Vector(x1,grad2,GoldN,CoeArea,CoeElas);
cek2[i]:=x2[1];
yek2[i]:=x2[2];
if (x0[1]==x2[1]) and (x0[2]<>x2[2]) then
grad3:=1/0; //divergent gradient, please subtitute vector
x3:=Gold_Opt_Func_2D_Vector_1(x2,1,GoldN,CoeArea,CoeElas);
else
grad3:=(x2[2]-x0[2])/(x2[1]-x0[1]);
x3:=Gold_Opt_Func_2D_Vector(x0,grad3,GoldN,CoeArea,CoeElas);
end if;
cek3[i]:=x3[1];
yek3[i]:=x3[2];
grad1:=grad2;
grad2:=grad3;
//Function Created
RatioZX:=CoeArea[1]*x3[1]^2+CoeArea[2]*x3[1]+CoeArea[3];
RatioZY:=CoeElas[1]*x3[2]^2+CoeElas[2]*x3[2]+CoeElas[3];
RatioZ[i]:=(RatioZX+RatioZY)/2;
CostZX:=CoeAreaCost[1]*x3[1]^2+CoeAreaCost[2]*x3[1]+CoeAreaCost[3];
CostZY:=CoeElasCost[1]*x3[2]^2+CoeElasCost[2]*x3[2]+CoeElasCost[3];
CostZ:=(CostZX+CostZY)/2;
x0:=x3;
error[i]:=abs(1-jos/RatioZ[i]);
jos:=RatioZ[i];
if error[i]<maxerror then
break;
end if;
end for;
end Powell_Method_Opt_Jos_Ratio;
|