Rai Zulfikar Satriagama

From ccitonlinewiki
Revision as of 14:23, 2 December 2020 by Rai Zulfikar Satriagama (talk | contribs) (→‎Review Pertemuan dan Tugas)
Jump to: navigation, search

Biodata Diri

Rai Zulfikar Satriagama.jpg

Nama  : Rai Zulfikar Satriagama

NPM  : 1906379075

Prodi  : Teknik Mesin S1 Reguler

TTL  : Tulungagung, 25 November 2001

Angkatan  : 2019

Hobi  : Membaca buku non fiksi

Assalamualaikum

Saya adalah salah satu ciptaan terbaik dari Tuhan Yang Maha Esa karena pada prinsipnya Tuhan Yang Maha Esa itu mendesain manusia dengan sebaik-baiknya makhluk. Saya memilih jurusan Teknik Mesin karena saya tertarik akan manufaktur dan bidang otomotif. Saya berharap dapat memaksimalkan semua kemampuan dan terus mengembangkan diri di Teknik Mesin UI. Output yang saya inginkan setelah lulus dari teknik mesin adalah dapat menjadi orang yang dapat memberikan bermanfaat kepada orang lain.

Metode Numerik

Metode Numerik merupakan mata kuliah yang saya ambil pada semester tiga ini. Metode numerik mempelajari teknik penyelesaian yang diformulasikan secara matematis dengan cara operasi hitungan. Pelajaran metode numerik menurut saya menarik karena saya jadi tahu asal mula regresi linear. Materi yang saya dapatkan dari Bapak Dr. Ir. Engkos A. Kosasih, M.T. sebelum UTS adalah

1. Pseudocode

2. Turunan Numerik

3. Regresi Linear

4. Deret Taylor dan Mclaurin

5. Interpolasi

Review Pertemuan dan Tugas

Rabu, 10-11-2020

Tujuan mempelajari metode numerik adalah:

1.Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik. Contoh: Persamaan aljabar, algorithma, pencocokan kurva, persamaan diferensial parsial, dll.

2.Mengerti aplikasi metode numerik.

3.Mampu menerapkan metode numerik dalam persoalan teknik.

4.Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab.


  • Tugas Pertama

Tugas pertama yang diberikan oleh Bapak Dr. Ir. Ahmad Indra Siswantara adalah membuat video tentang aplikasi open modelica. Pada tugas kali ini saya membuat video pengaplikasian rumus fisika (momen inersia) pada open modelica. Berikut merupakan video tugas pertama:


Rabu, 17-11-2020

Pada pertemuan kedua kelas Metode Numerik membahas mengenai tugas pertama yang sudah dikerjakan, beberapa mahasiswa mempresentasikan hasil tugasnya. Lalu kelas dilanjut dengan Pak Dai menjelaskan mengenai perbedaan dan fungsi dari model, class, dan fuction. Pak Dai berpesan bahwa kita sebagai manusia harus memiliki perubahan positif setiap harinya, hari ini harus lebih baik dari hari kemarin. Aplikasi open modelica ini free dan tidak berbayar sehingga dapat digunakan oleh siapa saja yang ingin belajar. Open Modelica mempunyai beberapa fitur, seperti membuat model, class, function, dan lain-lain. Aplikasi ini berupa object oriented, kita bisa membuat beberapa class fungsi dan class eksekusi, kemudian menggabungkannya menjadi satu model.

  • Tugas Kedua

Tugas kedua adalah dengan menggunakan aplikasi Open Modelica buatlah kelas fungsi aljabar simultan dengan variable array dan memanggil fungsi tersebut. Pada tugas ini saya memakai soal yang didapat dari internet mengenai sistem persamaan linear menggunakan metode eliminasi gauss. Berikut merupakan video tugas kedua:


Rabu, 25-11-2020

Pada pertemuan ketiga metode numerik ini diawali dengan review tugas yang telah diberikan di pertemuan kedua oleh beberapa mahasiswa. Selanjutnya Pak Dai memaparkan tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik, contohnya Computation Fluid Dynamics (CFD), Finite Element Analysis, dan Metode Stokastik. CFD dan FEA berbasis ilmu fisika, sementara metode stokastik berbasis data dan statistik. Ada lima langkah yang Pak Dai paparkan dalam mengaplikasikan metode numerik ke permasalahan teknik :

  • Riset masalah tekniknya terlebih dahulu
  • Menganalisis masalah (mendefinisikan variabel yang mau dicari dan mencari parameter fisikanya)
  • Membuat model matematika
  • Membuat model numerik
  • Setelah itu cari penyelesaian dengan bantuan komputer untuk mendapatkan output yang diinginkan

Setelah itu Pak Dai menyuruh Kami untuk mencoba membuat fungsi untuk menyelesaikan Persamaan 9.12 di buku Numerical Methods for Engineers 7th Edition oleh Chapra. Lalu, Kami latihan menyelesaikan sistem persamaan dengan membuat fungsi penyelesaian dengan cara pseudocode 9.4 untuk menjawab soal 9.5 yang ada di buku yang sama juga. Latihan yang kedua ini dimaksudkan agar Kami paham dalam penggunaan array dalam penggunaan Open Modelica, yang dimana array ini dapat memudahkan mengumpulkan himpunan penyelesaian.

  • Tugas Ketiga

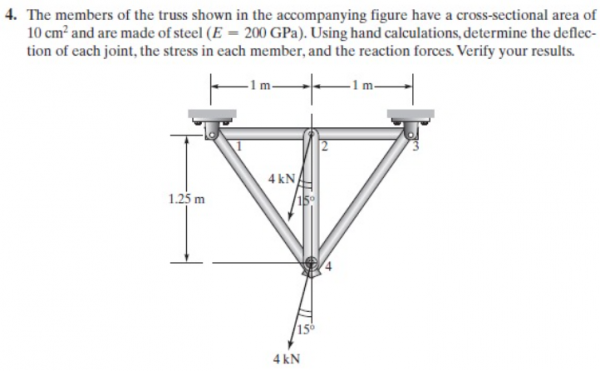
Tugas ketiga adalah menghitung soal statika struktur menggunakan aplikasi open modelica

Soal statur.png
  • Trusses
class Trusses_HW

parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary condition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses_HW;


  • Fungsi Panggil

Matrice Transformation 

function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
    
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness_Matrices;

Global Element Matrice 

function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
 for j in 1:B loop
     G[i,j]:=0;
 end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];

end Local_Global;

Reaction Matrice Equation 

function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
 if abs(X[i,1]) <= float_error then
   X[i,1] := 0;
 end if;
end for;

for i in 1:N loop
 Sol[i]:=X[i,1];
end for;

end Reaction_Trusses;

Gauss Jordan

function Gauss_Jordan

input Integer N;

input Real A[N,N];

input Real B[N];

output Real X[N];

Real float_error = 10e-10;

algorithm X:=Modelica.Math.Matrices.solve(A,B);

for i in 1:N loop 

 if abs(X[i]) <= float_error then
   X[i] := 0;
 end if;

end for;

end Gauss_Jordan;

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Rai_Zulfikar_Satriagama&oldid=45164"