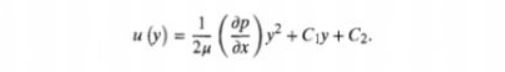Analytical solution of laminar flow through the parallel- plate

Studi kasus dan Terjemahan

Ref. Yijuan et. al, CFD - A Practical Approach, 1st ed., Elsevier

Terjemahan

Contoh 3.4 Anggaplah suatu aliran yang tunak, inkompresibel, dan laminar mengalir melewati pipa plat sejajar seperti yang diselidiki pada Contoh 3.2. Untuk fluida dengan properti yang konstan dan aliran berkembang penuh, Tentukan subjek profil kecepatan untuk kondisi batas di mana komponen vertikal v bernilai 0 di setiap titik.

Artikel 1 hasil diskusi : Governing Equation pada Fluida

Konsep mekanika fluida pada soal ini adalah tentang governing equation. Gover Equation adalah sebuah persamaan yang mengatur gerak laku dari fluida atau persamaan atur. Ada 3 governing equation pada fluida, yaitu:

Hukum Konservasi Energi (de/dt = W + Q) => energi yang masuk pada sistem akan sama dengan yang keluar, dengan energi yang keluar dapat berupa kerja atau panas.

Hukum Konservasi Massa (dm/dt = 0) => massa yang masuk pada sistem akan sama dengan massa yang keluar atau tidak adanya perubahan massa terhadap waktu.

Hukum Konservasi Momentum (m dv/dt = ∑ F) => jika pada sistem diberikan sebuah gaya, maka akan terjadi perubahan kecepatan partikelnya terhadap waktu atau dapat menimbulkan percepatan.

Aplikasinya ketiga rumus tersebut adalah, dapat dijadikan acuan dasar dalam perhitungan mekanika fluida.

Ahmad Mohammad Fahmi (1806181836)

Artikel 2 hasil diskusi : Pengenalan Aliran Viscous dan Pengamatan Aliran Fluida dengan Pendekatan Analitikal

Aliran dapat mengalir pada plat datar, plat paralel, tempat terbuka, dan lain-lain. Tentu penggunaannya tergantung pada pemakaian dan kondisi. Yang akan kita bahas kali ini adalah aliran fluida pada plat paralel yang sekarang dapat kita asumsikan sebagai sebuah pipa. Aliran yang mengalir pada kondisi wadah-wadah seperti diatas dapat dibagi menjadi 3 jenis, yaitu aliran laminar, aliran transisi dan aliran turbulen. Kita dapat mengidentifikasikan jenis tersebut dari yang disebut Bilangan Reynolds. Bilangan Reynolds dapat dilogikakan sebagai rasio antara gaya inersia dengan gaya viskositasnya. Aliran turbulen didapat pada Bilangan Reynolds dibawah 2300, Aliran transisi pada 2300 – 4000, dan aliran turbulen pada Bilangan Reynolds lebih dari 4000. Aliran laminar dan aliran turbulent pun memiliki penggunaannya masing-masing. Pada suatu material fluida, kita dapat memperoleh kondisi jenis aliran dengan pengaturan kecepatannya, karena tentu viskositasnya tidak berubah. Solusi lain adalah dengan penggunaan material yang lain apabila kondisi tidak memungkinkan. Pendekatan analitikal pada pengamatan aliran fluida adalah dengan menggunakan persamaan-persamaan matematika non linear yang cukup rumit. Kita dapat menggunakan metode Governing Equation yang dapat ditemukan pada hukum konservasi momentum, konservasi energi, dan konservasi massa yang menjadi dasar pada mekanika fluida. Pada aliran di antara plat paralel, kita dapat mengasumsikan kecepatan partikel fluida yang menyentuh plat=0 atau mendekatinya (no slip boundary condition) yang diakibatkan oleh gaya antar molekul. Hal ini dapat mempermudah kita dalam perhitungan saat menggunakan boundary condition.

Setiap material fluida akan berbeda-beda datanya untuk membentuk suatu jenis aliran. Pada suatu material fluida akan memiliki apa yang dinamakan “Critical Velocity” disinilah titik yang memisahkan dimana lapisan bergerak membentuk viscous/streamline flow dan apabila mulai melebihi, partikel fluida akan mulai bergerak secara acak dan gerakan lapisan-lapisan secara paralel akan mulai berpancar.

Bolonni Nugraha/1806181741

Artikel 3 hasil diskusi : Governing Equation pada Aliran

Soal tersebut membahas mengenai governing equation. Governing Equation adalah persamaan yang mengatur gerak laku fluida, bisa juga disebut persamaan atur. Ada tiga persamaan mengenai semua pergerakan aliran fluida yang ada di alam. Persamaan itu diantaranya konservasi massa, konservasi momentum, dan konservasi energi.

  A. Konservasi massa adalah Massa sistem akan selalu konstan dari waktu ke waktu. Rumusnya: dm/dt = 0. Contoh sederhananya adalah pipa dengan luas yang kecil kecepatannya lebih besar dibanding pipa dengan luas yang lebih besar. Alasannya karena massa harus konstan, sehingga pada pipa dengan luas yang lebih kecil, aliran terdorong lebih cepat.

  B. Hukum kekekalan momentum adalah kekalnya momentum pada sepanjang aliran, bisa berubah ke bentuk gaya ataupun sebaliknya. Hukum kekekalan momentum merupakan turunan dari hukum newton 2, rumusnya: m dV/dt = ΣF. Ada tiga gaya yang mempengaruhi gerakan fluida, yaitu gaya karena perbedaan tekanan, gaya gravitasi, dan gaya akibat gesekan fluida.

  C. Konservasi energi membahas apabila sistem energi mengalami perubahan total harus diikuti perubahan dalam bentuk kerja dan panas. Rumusnya:  dE/dt = W + Q

Aplikasi dari governing equation bisa diaplikasikan pada berbagai perhitungan mekanika fluida, karena setiap bahan mempunyai hasil yang berbeda-beda terhadap gaya dan enrgi yang diterapkan. Misalnya memprediksi aliran udara di sekitar pesawat atau mobil agar menimbulkan drag yang sedikit sehingga lebih hemat dalam bahan bakar. Contoh lainnya adalah penyusutan plastik pada proses injeksi molding. Proses tersebut perlu diperhitungkan prediksi alirannya.

Raditya Aryaputra Adityawarman (1806181691)

Artikel 4 hasil diskusi : Penggunaan Navier-Stokes untuk Aliran Laminer 2 Dimensi

Kasus ini membahas penggunaan governing equations, hukum kekekalan momentum, dan Navier-Stokes untuk mencari profil kecepatan suatu aliran

Dalam kasus dimana kecepatan vertikal (v) sama dengan nol dan komponen kecepatan horizontal (u) bergantung terhadap x, dapat dikatakan bahwa komponen u adalah fungsi dari y.

Hal ini dapat di buktikan dengan menggunakan rumus kontinuitas dari persamaan Navier-Stokes untuk aliran dua dimensi; Du/dx + dv/dy = 0 Du/dx + 0 = 0 Du/dx = 0

Kemudian, dengan menggunakan kondisi ini pada rumus momentum x, diketahui bahwa D2u/dy2 = 1/μ dp/dx

Dapat disimpulkan bahwa ketentuan untuk kekalan momentum pada kasus ini adalah persamaan gaya shear dan pressure.

Dengan menggunakan dua kali integral, di dapatkan kecepatan horizontal u terhadap y ; U(y) = 1/2μ (dp/dx) y2 + C1y + C2

Dan kondisi batas untuk menentukan C1 serta C2 adalah ; U = 0 untuk y = H/2 (no slip) Du/dy = 0 untuk y = 0 (simetris) Untuk kondisi simetris, didapatkan C1 = 0.

Maksud dari kondisi no slip disini adalah fluida dianggap sebagai fluida viskos. Diasumsikan bahwa pada solid boundary, fluida akan memilii kecepatan 0 terhadap dinding pipa. Menggunakan metode subtitusi, akan di dapatkan nilai C2 = -1/2μ (dp/dx) (H/2)2.

Dengannya profil kecepatan u(y) akan menjadi ; U (y) = 3/2 H2/12μ (-dp/dx) (1-(y2/(H/2)2)

Gradien kecepatan dp/dx disini bernilai negatif karena pressure berkurang disepanjang aliran. Hal ini disebabkan karena adanya pressure drop.

Untuk aplikasinya, soal ini dapat digunakan sebagai kasus simulasi untuk aliran air pada pipa secara dua dimensi.

-Elita Kabayeva, 19065435486-

Artikel 05 hasil diskusi : Analisis simultan distribusi menghasilkan berbagai solusi yang diperlukan

Pengembangan simultan distribusi kecepatan dan suhu untuk aliran laminar di dalam saluran pelat paralel dipelajari secara analitik, dengan mengadopsi prosedur linierisasi untuk masalah kecepatan dan menyelesaikan persamaan energi yang dipisahkan melalui teknik transformasi integral yang digeneralisasi. Solusi lengkap diperoleh dalam jangkauan luas dari koordinat aksial, dari evaluasi numerik sistem transformasi integral persamaan diferensial biasa. Selain itu, perkiraan solusi eksplisit disediakan untuk perkiraan cepat dalam konteks aplikasi. Beberapa aspek diselidiki, seperti pengaruh konveksi transversal, efek dari profil kecepatan yang berbeda, konvergensi solusi lengkap, dan akurasi solusi perkiraan.

Oleh : Hans Thiery T (1806233341)

Artikel 6 hasil diskusi : Konsep Aliran Luminar dan Penggunaan Governing Equation

Aliran laminar adalah aliran cairan atau gas dimana fluida melewati saluran secara teratur atau lancar. Kemudian pada aliran ini tekanan, kecepatan, dan property lainnya tetap pada keadaan yang konstan. Dalam dinamika fluida, aliran laminar ini terjadi ketika aliran fluida di lapisan parallel dengan tidak adanya gangguan antar lapisan. Aliran laminar ini juga mempunyai gerakan partikel yang sangat teratur dengan semua partikel bergerak dalam garis lurus sejajar dengan dinding pipa. Aliran laminar ini juga cenderung terjadi pada aliran yang mempunyai kecepatan yang rendah. Partikel fluida mengalir atau bergerak dengan bentuk garis lurus dan sejajar. Kemudian pada kecepatan rendah itu aliran laminar tergambar sebagai filamen panjang yang mengalir sepanjang aliran. Aliran laminar mempunyai bilangan Reynold lebih kecil dari 2300. Kemudian pada case nomor 1, aliran laminar dianggap steady dan incompressible melalui suatu plat parallel, maka fluida yang melewatiplat tersebut mempunyai kecepatan dan tekanan yang konstan di semua titik. Pada mekanika fluida terdapat 3 rumus dasar, yaitu hukum konservasi energi, hukum konservasi massa, dan hukum konservasi momentum.

Untuk analisis studi kasus tersebut digunakan konservasi momentum untuk menganalisis keceptasan fluida pada aliran laminar dalam plat parallel.

Oleh : Rasyid Indy Nur Sasongko (1806181874)

Artikel 7 hasil diskusi: Hubungan Hukum Konservasi Momentum Terhadap Analytical Solution of Laminar Flow

Terdapat tiga hukum dasar yang digunakan dalam menurunkan rumus-rumus dalam mekanika fluida. Hukum konservasi energi, hukum konservasi momentum, hukum konservasi massa. Konservasi Energi didefinisikan sebagai laju perubahan energi harus diikuti dengan perubahan dalam bentuk kerja(work) dan panas (heat), Hukum konservasi massa dapat didefinisikan sebagai perubahan massa terhadap waktu sama dengan 0, tidak ada yang dibuat dan tidak ada yang dihilangkan, sedangkan Hukum konservasi momentum dapat didefinisikan sebagai gaya netto sama dengan massa dikali laju perubahan kecepatan. Untuk analisis studi kasus tersebut, digunakan hukum konservasi momentum untuk menganalisis kecepatan fluida pada aliran laminar dalam plat parallel. Momentum Equation tersebut dapat ditulis sebagai berikut:

Namun karena aliran laminar tersebut diasumsikan bergerak halus pada satu sumbu, maka komponen y dan z dapat diabaikan. Sehingga dapat dilihat bahwa factor-faktor yang mempengaruhi aliran laminar fluida ada 3 yaitu, gaya akibat tekanan, gaya akibar gravitasi, dan gaya viskos.

Oleh: Edward Joshua Patrianus Mendrofa (1806233354)

Artikel 8 hasil diskusi: Governing Equation

Governing equation adalah persamaan yang mengatur pergerakan-pergerakan dari fluida. Persamaan-persamaan yang mengatur pergerakan fluida tersebut adalah sebagai berikut :

a. konservasi massa, bahwa pada suatu sistem tertutup massa akan konstan meskipun terjadi berbagai aktivitas pada sistem tersebut sehingga dapat disimpulkan bahwa massa zat sebelum dan sesudah adalah sama, tidak bertambah ataupun berkurang. (dM/dt = 0)

b. Konservasi energi, bahwa energi tidak dapat ditambah atau dihilangkan namun energi dapat diubah bentuknya. (dE/dt = W + Q )

c. Konservasi momentum, bahwa momentum total 2 (dua) buah benda yang bertumbukan sebelum dan sesudahnya adalah sama, dengan kata lain momentum totalnya adalah konstan. (m . dV/dt = ΣF )

Oleh : Ikhsanul Fikri Fakhrurrozi (1906435510)

Artikel 9 hasil diskusi: Governing Equation

Konsep yang digunakan pada soal no 1 adalah Governing Equation pada fluida. Mengatur tentang aliran fluida. Ada 3 Governing equation pada fluida:

a. Hukum konservasi massa (dm/dt = 0) massa yang masuk sistem akan sama dengan massa yang keluar sistem.

b. Hukum konservasi momentum (∑F = m.a atau m.dv/dt = ∑F) suatu sistem mengalami percepatan apabila ada gaya (tidak sama dengan nol)

c. Hukum konservasi energi (dE/dt = W + Q) energi yang masuk sistem akan sama dengan yang keluar sistem, energi tersebut berupa energi panas dan kerja.

Oleh: Muhammad Fairuz Daffa (1806181716)

Artikel 10 hasil diskusi: Governing equation fluida

Persamaan pembentuk aliran yang mendasar untuk aliran fluida dan perpindahan panas adalah dikembangkan dari tiga hukum kekekalan dalam fisika. Hukum kekekalan tersebut adalah, kekekalan massa, kekekalan momentum, dan kekekalan energi.

1. Hukum kekekalan massa (dm/dt = 0) Massa sistem akan selalu konstan dari waktu ke waktun tidak akan ada perubahan massa dalam aliran

2. Hukum kekekalan momentum (m dv/dt = ∑ F) jika pada sistem diberikan sebuah gaya, maka akan terjadi perubahan kecepatan partikelnya terhadap waktu atau dapat menimbulkan percepatan.

3. Hukum konservasi energi (de/dt = W + Q) prinsip fisik ketiga yaitu energi yang di konservasi diterapkan. Menyatakan perubahan tingkat energi di dalam (E) sebuah elemen adalah sama dengan jumlah dari fluks panas bersih (Q) kedalam elemen dan tingkat kerja yang dilakukan W pada elemen oleh body dan kekuatan permukaan.

Mohammad Varian (1606907713)

Artikel 10 hasil diskusi: Persamaan pada Mekanika Fluida

Pada mekanika fluida terdapat 3 rumus dasar, yaitu Hukum Konservasi Energi, Hukum Konservasi Massa, dan Hukum Konservasi Momentum.

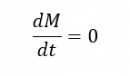
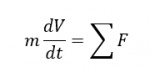
Governing Equation merupakan persamaan yang menjelaskan baagaimana nilai dari variabel yang tidak diketahui (dependent) ketika variabel yang diketahui (independent) berubah. Pada pembahasan Example 3.4 ini dapat dilihat bahwa solusi ini merupakan Governing Equation yang didapatkan dari menurunkan Hukum Kekekalan Massa dan Hukum Kekekalan Energi.

Apabila terdapat detail viskositas, jarak plat, dan sebagainya kita dapat memprediksi solusi yang ada pada pembahasan menggunakan Navier-Stokes Equation. Persamaan ini menjelaskan bagaimana hubungan kecepatan, tekanan, temperatur, dan massa jenis fluida bergerak.

Oleh: Virsya Pramesti Salsabila - 1806181760