Metode Numerik - Josiah Enrico S (1906356286)

Intro - Metode Numerik/11 November 2020

Tujuan belajar metode numerik yaitu agar penulis dapat:

1) Memahami konsep dan prinsip dasar metode numerik.

2) Memahami aplikasi metode numerik

3) Menyelesaikan persoalan teknik dengan metoda numerik

4) Mendapat nilai tambah sebagai manusia yang lebih beradab

Aplikasi Modelica - Metode Numerik/18 November 2020

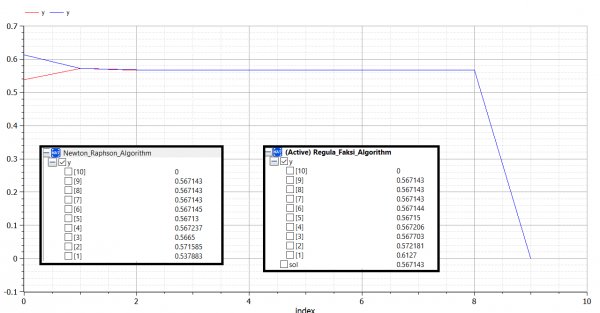
Berikut ini adalah contoh penerapan aplikasi OpenModelica untuk membuat 4 algoritma metode numerik dalam mencari roots of equation (akar persamaan) dari:

f(x) = exp^(-x)-(x)

f'(x) = -exp^(-x)-1

error maksimum = 0.0000001

1) Newton Raphson (Terbuka)

model Newton_Raphson_Algorithm

parameter Real g=1; //guess
parameter Integer N=20; //max iteration
parameter Real er=0.0000001; //error maximum
Real a[N]; 
Real y[N];//function
Real ER[N]; //error
Real sol; //solution

algorithm

a[1]:=g;
y[1]:=a[1]-(exp(-a[1])-a[1])/(-exp(-a[1])-1);
ER[1]:=abs(1-a[1]/y[1]);

for i in 2:N loop
  a[i]:=y[i-1];
  y[i]:=a[i]-(exp(-a[i])-a[i])/(-exp(-a[i])-1);
  ER[i]:=abs(1-y[i-1]/y[i]);

  if ER[i]<er then
 sol:=y[i];
 break;
 end if;
end for;

end Newton_Raphson_Algorithm;

2) Secant (Terbuka)

model Secant_Algorithm

parameter Real a=0; //guess
parameter Real b=1; //guess
parameter Integer N=10; //max iteration
parameter Real er=0.0000001; //error maximum
Real A[N];
Real B[N];
Real y[N];
Real ER[N];
Real sol; //solution

algorithm

A[1]:=a;
B[1]:=b;
y[1]:=B[1]-(exp(-B[1])-B[1])*(A[1]-B[1])/((exp(-A[1])-A[1])-(exp(-B[1])-B[1]));
ER[1]:=abs(1-B[1]/y[1]);

for i in 2:N loop
 A[i]:=B[i-1];
 B[i]:=y[i-1];
 y[i]:=B[i]-(exp(-B[i])-B[i])*(A[i]-B[i])/((exp(-A[i])-A[i])-(exp(-B[i])-B[i]));
 ER[i]:=abs(1-y[i-1]/y[i]);

 if ER[i]<er then
 sol:=y[i];
 break;
 
 end if;
end for;

end Secant_Algorithm;

3) Bisection (Tertutup)

model Bisection_Algorithm

parameter Real a=0; //guess bawah
parameter Real b=1; //guess atas
parameter Integer N=50; //max iteration
parameter Real er=0.0000001; //error maximum
Real fa=(exp(-a)-a);
Real fb=(exp(-b)-b);
Real A[N];
Real B[N];
Real fy[N];
Real y[N];
Real ER[N];
Real sol; //solution

algorithm

if fa*fb<0 then

A[1]:=a;
B[1]:=b;
y[1]:=(A[1]+B[1])/2;
fy[1]:=exp(-y[1])-y[1];
ER[1]:=1;

for i in 2:N loop
 if fy[i-1]>0 then
 A[i]:=y[i-1];
 B[i]:=B[i-1];
 else
 A[i]:=A[i-1];
 B[i]:=y[i-1];
 end if;
   
 y[i]:=(A[i]+ B[i])/2;
 fy[i]:=exp(-y[i])-y[i];
 ER[i]:=abs(1-y[i-1]/y[i]);
 
 if ER[i]<er then
 sol:=y[i];
 break;
 end if;

end for;
end if;

end Bisection_Algorithm;

4) Regula Falsi (Tertutup)

model Regula_Falsi_Algorithm

parameter Real a=0; //guess bawah
parameter Real b=1; //guess atas
parameter Integer N=20; //max iteration
parameter Real er=0.0000001; //error maximum
Real A[N];
Real B[N];
Real fa[N];
Real fb[N];
Real fy[N];
Real y[N];
Real ER[N];
Real sol; //solution

algorithm

A[1]:=a;
B[1]:=b;
fa[1]:=exp(-A[1])-A[1];
fb[1]:=exp(-B[1])-B[1]; 

if fa[1]*fb[1]<0 then 

y[1]:=(A[1]*fb[1]-B[1]*fa[1])/(fb[1]-fa[1]);
fy[1]:=exp(-y[1])-y[1];
ER[1]:=1; 

for i in 2:N loop
 if fy[i-1]>0 then
 A[i]:=y[i-1];
 B[i]:=B[i-1];
 else
 A[i]:=A[i-1];
 B[i]:=y[i-1];
 end if;
 
 fa[i]:=exp(-A[i])-A[i];
 fb[i]:=exp(-B[i])-B[i];
 y[i]:=(A[i]*fb[i]-B[i]*fa[i])/(fb[i]-fa[i]);
 fy[i]:=exp(-y[i])-y[i];
 ER[i]:=abs(1-y[i-1]/y[i]);
 
 if ER[i]<er then
 sol:=y[i];
 break;
 end if;
end for;
end if;
 
end Regula_Falsi_Algorithm;

Berikut link Youtube yang berisi penjelasan tentang algoritma dan penulisan kode OpenModelica keempat metode diatas:

Fungsi Panggil dalam Modelica - Metode Numerik/18 November 2020

Fungsi panggil dalam aplikasi Modelica adalah metode membuat fungsi numerik dalam kelas function yang akan digunakan di dalam permodelan numerik utama (tipe 'class'). metode ini biasanya dipakai untuk menyederhanakan persoalan matematika yang kompleks, seperti persamaan aljabar simultan, sehingga lebih mudah diselesaikan. Dalam artikel ini akan ditampilkan 3 contoh persoalan numerik dengan solusi array atau lebih dari satu anggota:

1) Root of Equation (Newton Raphson dan Regula Falsi)

Grafik Modelica

Newton Raphson ... algorithm a[1]:=g; y[1]:=a[1]-(Fungsi(a[1]))/(Der_Fungsi(a[1])); ER[1]:=abs(1-a[1]/y[1]); for i in 2:N loop a[i]:=y[i-1]; y[i]:=a[i]-(Fungsi(a[i]))/(Der_Fungsi(a[1])); ER[i]:=abs(1-y[i-1]/y[i]); if ER[i]<er then sol:=y[i]; break; end if; Regula Falsi ... fa[1]:=Fungsi(A[1]); fb[1]:=Fungsi(B[1]); if fa[1]*fb[1]<0 then y[1]:=(A[1]*fb[1]-B[1]*fa[1])/(fb[1]-fa[1]); fy[1]:=Fungsi(y[1]); ER[1]:=1; ... fa[i]:=Fungsi(A[i]); fb[i]:=Fungsi(B[i]); y[i]:=(A[i]*fb[i]-B[i]*fa[i])/(fb[i]-fa[i]); fy[i]:=Fungsi(y[i]); ER[i]:=abs(1-y[i-1]/y[i]); ...

fungsi function Fungsi input Real X; output Real Y; algorithm Y:=exp(-X)-X; end Fungsi; fungsi turunan function Der_Fungsi input Real X; output Real Y; algorithm Y:=-exp(-X)-1; end Der_Fungsi;

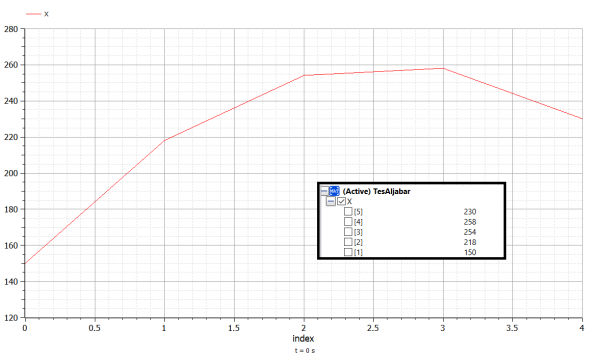
2) Heat Diffusion

Referensi: Versteeg, H. K., Malalasekera, W. (2007). An Introduction to Computational Fluid Dynamics. 2nd Edition. Harlow: Pearson (Example 4.2)

Grafik Modelica

Persamaan class TesAljabar parameter Real A[5,5]=[375,-125,0,0,0; -125,250,-125,0,0; 0,-125,250,-125,0; 0,0,-125,250,-125; 0,0,0,-125,375]; parameter Real B[5]={29000,4000,4000,4000,54000}; Real X[5]; equation X=matriks5(A,B); end TesAljabar;

fungsi function matriks5 input Real A[5,5]; input Real B[5]; output Real X[5]; algorithm X:=Modelica.Math.Matrices.solve(A,B); end matriks5;

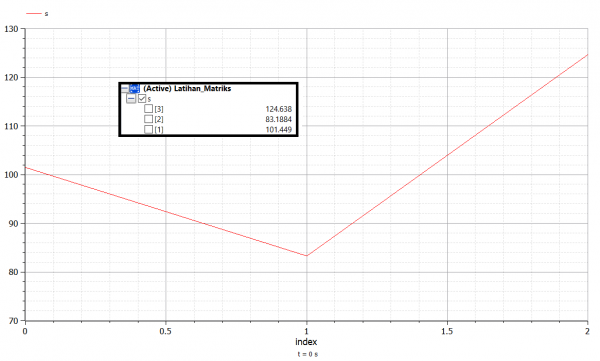
3) Combined Spring Stiffness

Referensi: http://www.sharetechnote.com/html/EngMath_Matrix_FEM_ComplicatedSpring.html

Grafik Modelica

Persamaan class Latihan_Matriks parameter Real c1=1; //spring 1 parameter Real c2=2; //spring 2 parameter Real c3=3; //spring 3 parameter Real c4=4; //spring 4 parameter Real c5=5; //spring 5 parameter Real k1[3,3]=c1*[1,0,0; 0,0,0; 0,0,0]; parameter Real k2[3,3]=c2*[1,-1,0; -1,1,0; 0,0,0]; parameter Real k3[3,3]=c3*[1,-1,0; -1,1,0; 0,0,0]; parameter Real k4[3,3]=c4*[1,0,-1; 0,0,1; -1,0,1]; parameter Real k5[3,3]=c5*[0,0,0; 0,1,-1; 0,-1,1]; parameter Real B[3]={100,200,300}; Real K[3,3]; Real s[3]; algorithm K:=k1+k2+k3+k4+k5; s:=matriks3(K,B); end Latihan_Matriks;

fungsi function matriks3 input Real A[3,3]; input Real B[3]; output Real X[3]; algorithm X:=Modelica.Math.Matrices.solve(A,B); end matriks3;

Berikut link Youtube yang berisi penjelasan tentang algoritma dan penulisan kode OpenModelica latihan diatas:

Berikut juga adalah pemodelan Modelica untuk metode Naive Gauss:

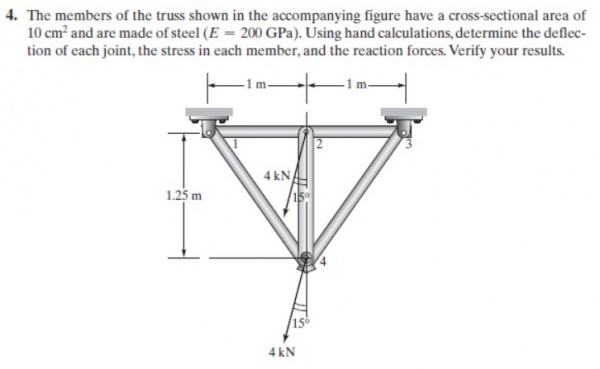
Finite Element Method for Trusses - Metode Numerik/2 Desember 2020

Berikut 2 contoh penggunaan aplikasi Modelica untuk menyelesaikan perhitungan displacement dan reaction force pada trusses:

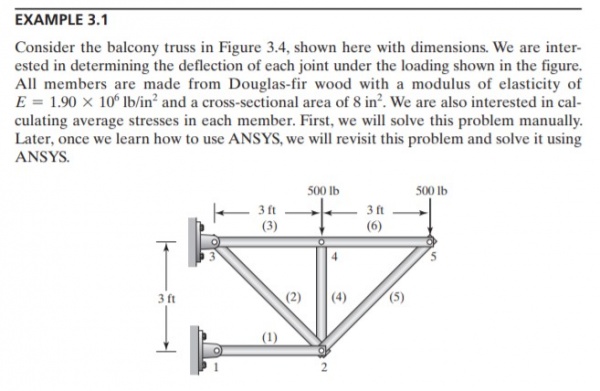
Trusses Problem 1 (Example 3.1)

Grafik Displacement

Grafik Reaction Forces

Persamaan model Trusses parameter Integer N=10; //Global matrice = 2*points connected parameter Real A=8; parameter Real E=1.9e6; Real G[N,N]; //global Real Ginitial[N,N]; //global Real Sol[N]; //global dispplacement Real X[N]={0,0,0,0,0,0,0,-500,0,-500}; Real R[N]; //global reaction force Real SolMat[N,1]; Real XMat[N,1]; //boundary coundition Integer b1=1; Integer b2=3; //truss 1 parameter Real X1=0; //degree between truss Real k1=A*E/36; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N]; //truss 2 parameter Real X2=135; //degree between truss Real k2=A*E/50.912; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N]; //truss 3 parameter Real X3=0; //degree between truss Real k3=A*E/36; Real K3[4,4]; //stiffness matrice Integer p3a=3; Integer p3b=4; Real G3[N,N]; //truss 4 parameter Real X4=90; //degree between truss Real k4=A*E/36; Real K4[4,4]; //stiffness matrice Integer p4a=2; Integer p4b=4; Real G4[N,N]; //truss 5 parameter Real X5=45; //degree between truss Real k5=A*E/50.912; Real K5[4,4]; //stiffness matrice Integer p5a=2; Integer p5b=5; Real G5[N,N]; //truss 6 parameter Real X6=0; //degree between truss Real k6=A*E/36; Real K6[4,4]; //stiffness matrice Integer p6a=4; Integer p6b=5; Real G6[N,N]; /* for each truss, please ensure pXa is lower then pXb (X represents truss element number) */ algorithm //creating global matrice K1:=Stiffness_Matrices(X1); G1:=k1*Local_Global(K1,N,p1a,p1b); K2:=Stiffness_Matrices(X2); G2:=k2*Local_Global(K2,N,p2a,p2b); K3:=Stiffness_Matrices(X3); G3:=k3*Local_Global(K3,N,p3a,p3b); K4:=Stiffness_Matrices(X4); G4:=k4*Local_Global(K4,N,p4a,p4b); K5:=Stiffness_Matrices(X5); G5:=k5*Local_Global(K5,N,p5a,p5b); K6:=Stiffness_Matrices(X6); G6:=k6*Local_Global(K6,N,p6a,p6b); G:=G1+G2+G3+G4+G5+G6; Ginitial:=G; //implementing boundary condition for i in 1:N loop G[2*b1-1,i]:=0; G[2*b1,i]:=0; G[2*b2-1,i]:=0; G[2*b2,i]:=0; end for; G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1; //solving displacement Sol:=Gauss_Jordan(N,G,X); //solving reaction force SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); end Trusses;

Trusses Problem 2 (Homework)

Grafik Displacement

Grafik Reaction Forces

Persamaan class Trusses_HW parameter Integer N=8; //Global matrice = 2*points connected parameter Real A=0.001; //Area m2 parameter Real E=200e9; //Pa Real G[N,N]; //global Real Ginitial[N,N]; //global Real Sol[N]; //global dispplacement Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; Real R[N]; //global reaction force Real SolMat[N,1]; Real XMat[N,1]; //boundary condition Integer b1=1; Integer b2=3; //truss 1 parameter Real X1=0; //degree between truss Real k1=A*E/1; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N]; //truss 2 parameter Real X2=0; //degree between truss Real k2=A*E/1; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N]; //truss 3 parameter Real X3=90; //degree between truss Real k3=A*E/1.25; Real K3[4,4]; //stiffness matrice Integer p3a=2; Integer p3b=4; Real G3[N,N]; //truss 4 parameter Real X4=90+38.6598; //degree between truss Real k4=A*E/1.6; Real K4[4,4]; //stiffness matrice Integer p4a=1; Integer p4b=4; Real G4[N,N]; //truss 5 parameter Real X5=90-38.6598; //degree between truss Real k5=A*E/1.6; Real K5[4,4]; //stiffness matrice Integer p5a=3; Integer p5b=4; Real G5[N,N]; /* for each truss, please ensure pXa is lower then pXb (X represents truss element number) */ algorithm //creating global matrice K1:=Stiffness_Matrices(X1); G1:=k1*Local_Global(K1,N,p1a,p1b); K2:=Stiffness_Matrices(X2); G2:=k2*Local_Global(K2,N,p2a,p2b); K3:=Stiffness_Matrices(X3); G3:=k3*Local_Global(K3,N,p3a,p3b); K4:=Stiffness_Matrices(X4); G4:=k4*Local_Global(K4,N,p4a,p4b); K5:=Stiffness_Matrices(X5); G5:=k5*Local_Global(K5,N,p5a,p5b); G:=G1+G2+G3+G4+G5; Ginitial:=G; //implementing boundary condition for i in 1:N loop G[2*b1-1,i]:=0; G[2*b1,i]:=0; G[2*b2-1,i]:=0; G[2*b2,i]:=0; end for; G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1; //solving displacement Sol:=Gauss_Jordan(N,G,X); //solving reaction force SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); end Trusses_HW;

Fungsi Panggil

Matrice Transformation function Stiffness_Matrices input Real A; Real Y; output Real X[4,4]; Real float_error = 10e-10; final constant Real pi=2*Modelica.Math.asin(1.0); algorithm Y:=A/180*pi; X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y); Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2; -(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y); -Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2]; for i in 1:4 loop for j in 1:4 loop if abs(X[i,j]) <= float_error then X[i,j] := 0; end if; end for; end for; end Stiffness_Matrices;

Global Element Matrice function Local_Global input Real Y[4,4]; input Integer B; input Integer p1; input Integer p2; output Real G[B,B]; algorithm for i in 1:B loop for j in 1:B loop G[i,j]:=0; end for; end for; G[2*p1,2*p1]:=Y[2,2]; G[2*p1-1,2*p1-1]:=Y[1,1]; G[2*p1,2*p1-1]:=Y[2,1]; G[2*p1-1,2*p1]:=Y[1,2]; G[2*p2,2*p2]:=Y[4,4]; G[2*p2-1,2*p2-1]:=Y[3,3]; G[2*p2,2*p2-1]:=Y[4,3]; G[2*p2-1,2*p2]:=Y[3,4]; G[2*p2,2*p1]:=Y[4,2]; G[2*p2-1,2*p1-1]:=Y[3,1]; G[2*p2,2*p1-1]:=Y[4,1]; G[2*p2-1,2*p1]:=Y[3,2]; G[2*p1,2*p2]:=Y[2,4]; G[2*p1-1,2*p2-1]:=Y[1,3]; G[2*p1,2*p2-1]:=Y[2,3]; G[2*p1-1,2*p2]:=Y[1,4]; end Local_Global;

Reaction Matrice Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; Gauss Jordan function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop if abs(X[i]) <= float_error then X[i] := 0; end if; end for; end Gauss_Jordan;

Kuis Membuat Class FLowchart - Metode Numerik/18 November 2020

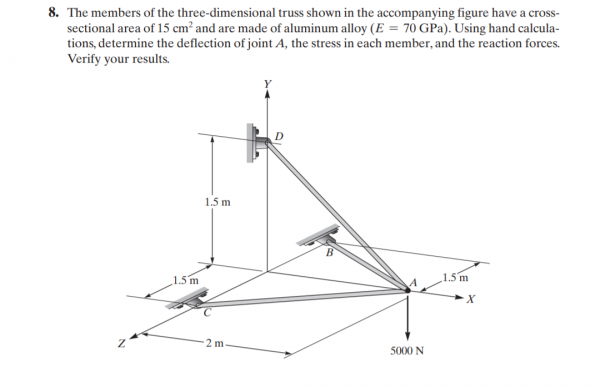
3D Trusses - Metode Numerik/18 November 2020

Master class Trusses3D_Tes //define initial variable parameter Integer Points=4; //Number of Points parameter Integer Trusses=3; //Number of Trusses parameter Real Area=0.0015; //Area parameter Real Elas=70e9; //Elasticity //define connection parameter Integer C[Trusses,2]=[1,2; 1,3; 1,4]; //define coordinates (please put orderly) parameter Real P[Points,3]=[2,0,0; 0,0,1.5; 0,0,-1.5; 0,1.5,0]; //define external force (please put orderly) parameter Real F[Points*3]={0,-5000,0, 0,0,0, 0,0,0, 0,0,0}; //define boundary parameter Integer b[:]={2,3,4}; //solution Real displacement[N], reaction[N]; protected parameter Integer N=3*Points; Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b); Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, X[3,3]; algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop for j in 1:3 loop q1[j]:=P[C[i,1],j]; q2[j]:=P[C[i,2],j]; end for; //Solving Matrix L:=Modelica.Math.Vectors.length(q2-q1); cx:=(q2[1]-q1[1])/L; cy:=(q2[2]-q1[2])/L; cz:=(q2[3]-q1[3])/L; X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; cy*cx,cy^2,cy*cz; cz*cx,cz*cy,cz^2]; //Transforming to global matrix g:=zeros(N,N); for m,n in 1:3 loop g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; end for; G_star:=G+g; G:=G_star; end for; //Implementing boundary for i in boundary loop for j in 1:N loop G[i,j]:=id[i,j]; end for; end for; //Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F); //Solving reaction reaction:=(G_star*displacement)-F; //Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; end for; end Trusses3D_Tes;

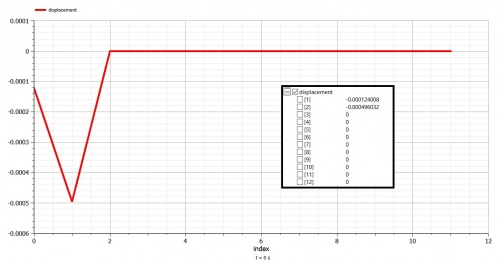
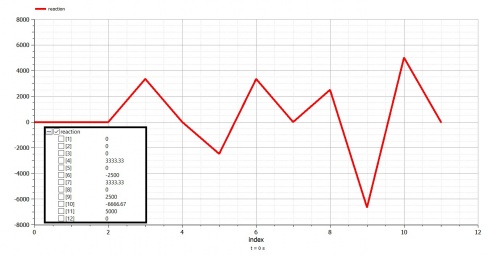
Berikut adalah hasil simulasi yang dilakukan:

Berikut link Youtube yang berisi penjelasan tentang algoritma dan penulisan kode OpenModelica metode diatas:

Optimization - Metode Numerik/16 November 2020

Function to be solved

function Func_Optimization
input Real x;
import Modelica.Math;
output Real y;

algorithm
y:=2*sin(x)-x^2/10;

end Func_Optimization;

Optimization - Golden Section

model Opt_Gold

parameter Real xlo=0;
parameter Real xhi=4; 
parameter Integer N=8; // maximum iteration
parameter Real es=0.0001; // maximum error

Real f1[N], f2[N], x1[N], x2[N], ea[N];
Real xopt,  fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;

algorithm
xl := xlo; 
xu := xhi;
 
for i in 1:N loop
 d:= R*(xu-xl);
 x1[i]:=xl+d;
 x2[i]:=xu-d;
 f1[i]:=Func_Optimization(x1[i]);
 f2[i]:=Func_Optimization(x2[i]);
 xint:=xu-xl;
 
 if f1[i]>f2[i] then
   xl:=x2[i];
   xopt:=x1[i];
   fx:=f1[i];
   else
     xu:=x1[i];
     xopt:=x2[i];
     fx:=f2[i];
 end if;
 
 ea[i]:=(1-R)*abs((xint)/xopt);
 if ea[i]<es then
   break;
 end if;
end for;

end Opt_Gold;

Optimization - Newton

model Opt_Newton

parameter Real g=2.5; //initial guess
parameter Integer N=8; // maximum iteration
parameter Real es=0.0001; // maximum error

Real X[N];
Real xopt, fx, ea[N];

algorithm
X[1]:=g;
ea[1]:=1;

for i in 2:N loop
 X[i]:=X[i-1]-Func_Optimization_Der(X[i-1])/Func_Optimization_Der_Der(X[i-1]);
 xopt:=X[i];
 
 ea[i]:=abs(1-X[i-1]/X[i]);
 if ea[i]<es then
   break;
 end if;
end for;
fx:=Func_Optimization(xopt);

end Opt_Newton;

Optimization - Parabolic

model Opt_Parabolic

parameter Real g1=0; //initial guess
parameter Real g2=1; //initial guess
parameter Real g3=4; //initial guess
parameter Integer N=5; // maximum iteration
parameter Real es=0.0001; // maximum error

Real x1, x2, x3, xopt, xp[N], ea[N];
//Real xl, xm, xu;
Real fx1, fx2, fx3, fx, A[4], A_star[4];
algorithm
x1:=g1;
x2:=g2;
x3:=g3;

for i in 1:N loop
 fx1:=Func_Optimization(x1);
 fx2:=Func_Optimization(x2);
 fx3:=Func_Optimization(x3);
 
 xp[i]:=(fx1*(x2^2-x3^2)+fx2*(x3^2-x1^2)+fx3*(x1^2-x2^2))/(2*fx1*(x2-x3)+2*fx2*(x3-x1)+2*fx3*(x1-x2));
 xopt:=xp[i];
 fx:=Func_Optimization(xp[i]);
 A:={x1,x2,x3,xp[i]};
 A_star:=Modelica.Math.Vectors.sort(A);
  
 if xp[i]>x2 then
   x1:=A_star[2];
   x2:=A_star[3];
   x3:=A_star[4];
   else
     x1:=A_star[1];
     x2:=A_star[2];
     x3:=A_star[3];
 end if;
end for;

ea[1]:=1;
for i in 2:N loop  
 ea[i]:=abs(1-xp[i-1]/xp[i]);
 if ea[i]<es then
   break;
 end if;
end for;

end Opt_Parabolic;

Jawaban UAS 2021 - Josiah Enrico S

No 1

Langkah-lanhkah optimasi

1. Tentukan tujuan optimasi lalu definisikan semua parameter yang ada.

1. Menentukan boundary dan constraint pada struktur

1. Menentukan asumsi dalam permodelan struktur

1. Melakukan analisa struktur (komputasi)

1. Setelah mendapat persamaan utama, variasikan nilai objektif yang akan dioptimasi

1. Gunakan metode optimasi yang sesuai

1. Setelah mendapatakan nilai optimasi, lakukan pengujian variabel dengan analisa

1. Jika hasilnya memuaskan, optimasi selesai. Jika hasilnya belum memuaskan, ulangi dari langkah 6

No 2

Tujuan Optimasi:

• Mengoptimasi kekuatan material struktur dan dinding water tank

Asumsi:

• Fluida Statis

• Gravitasi: 9,81 m/s2

• Fluida: air murni (rho = 1000 kg/m3)

Dalil Fisika

• Gaya Hidrostatis F = rho*g*V

• Stress = E*Strain

No 3

Simulasi Dengan Perbedaan Massa Jenis

Persamaan aljabar lokal tiap elemen	Persamaan aljabar global tiap elemen
Truss A (1 to 2) [ 0 0 0 0 ] (1x) k = (A*E/L) [ 0 1 0 1 ] (1y) [ 0 0 0 0 ] (2x) [ 0 -1 0 -1 ] (2y)	Truss A (1 to 2) [ 0 0 0 0 0 0 0 0 ] (1x) [ 0 1 0 1 0 0 0 0 ] (1y) [ 0 0 0 0 0 0 0 0 ] (2x) k = (A*E/L) [ 0 -1 0 -1 0 0 0 0 ] (2y) [ 0 0 0 0 0 0 0 0 ] (3x) [ 0 0 0 0 0 0 0 0 ] (3y) [ 0 0 0 0 0 0 0 0 ] (4x) [ 0 0 0 0 0 0 0 0 ] (4y)
Truss B (2 to 3) [ 0.5 0.5 -0.5 -0.5 ] (2x) k = (A*E/L) [ 0.5 0.5 -0.5 -0.5 ] (2y) [-0.5 -0.5 0.5 0.5 ] (3x) [-0.5 -0.5 0.5 0.5 ] (3y)	Truss B (2 to 3) [ 0 0 0 0 0 0 0 0 ] (1x) [ 0 0 0 0 0 0 0 0 ] (1y) [ 0 0 0.5 0.5 -0.5 -0.5 0 0 ] (2x) k = (A*E/L) [ 0 0 0.5 0.5 -0.5 -0.5 0 0 ] (2y) [ 0 0 -0.5 -0.5 0.5 0.5 0 0 ] (3x) [ 0 0 -0.5 -0.5 0.5 0.5 0 0 ] (3y) [ 0 0 0 0 0 0 0 0 ] (4x) [ 0 0 0 0 0 0 0 0 ] (4y)
Truss C (2 to 4) [ 0.5 -0.5 -0.5 0.5 ] (2x) k = (A*E/L) [-0.5 0.5 0.5 -0.5 ] (2y) [-0.5 0.5 0.5 -0.5 ] (4x) [ 0.5 -0.5 -0.5 0.5 ] (4y)	Truss C (2 to 4) [ 0 0 0 0 0 0 0 0 ] (1x) [ 0 0 0 0 0 0 0 0 ] (1y) [ 0 0 0.5 -0.5 0 0 -0.5 0.5 ] (2x) k = (A*E/L) [ 0 0 -0.5 0.5 0 0 0.5 -0.5 ] (2y) [ 0 0 0 0 0 0 0 0 ] (3x) [ 0 0 0 0 0 0 0 0 ] (3y) [ 0 0 -0.5 0.5 0 0 0.5 -0.5 ] (4x) [ 0 0 0.5 -0.5 0 0 -0.5 0.5 ] (4y)

Persamaan aljabar lokal tiap elemen

Persamaan aljabar global tiap elemen