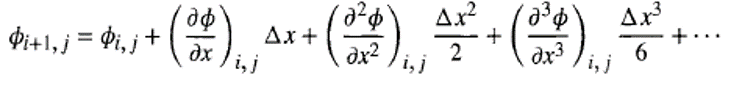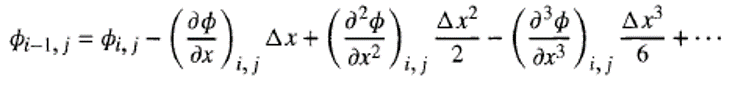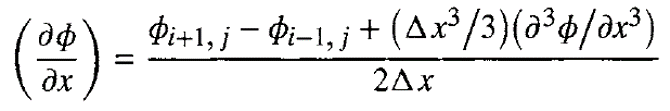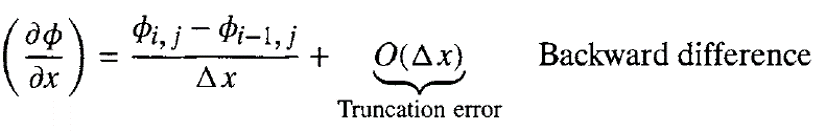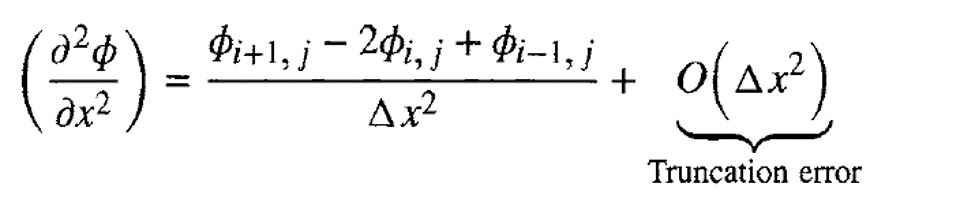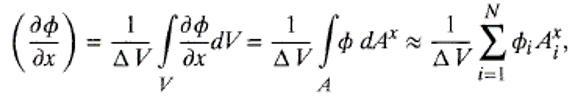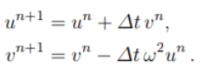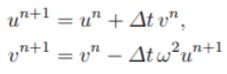Muhammad Hilman Gumelar Syafei

بِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيم 

Informasi Singkat

Alhamdulillah, segala puji bagi Allah Ta'ala, atas karunianya saya bisa membuat page di wiki ini. Shalawat serta salam senantiasa kita ucapkan kepada nabi Muhammad Shalallahu 'alaihi wasallam Perkenalkan, nama saya Edo, Informasi singkat mengenai saya bisa dilihat sebagai berikut:

Nama  : Muhammad Hilman Gumelar Syafei

Pendidikan Terakhir : Teknik Mesin - Sarjana

Email  : edoalbamusic@gmail.com

No. HandPhone  : 087889337317

TOPIK RISET  : Pengembangan Teknologi FCC (Fluid Catalytic Cracking) pada aplikasi Zero Energy Building

Insyaa Allah di page ini, saya akan berbagi informasi mengenai aktivitas studi dan penelitian saya. Saya dengan senang hati menerima kritikan dan masukan dari teman-teman semua. Semoga bermanfaat :D

Aktivitas

Saat ini, saya sedang aktiv mengambil kuliah magister Jurusan Teknik Mesin di Universitas Indonesia, dengan bidang peminatan Konversi Energi. Tema penelitian yang saya adalah aplikasi Zero energy Building, dan topik penelitian saya adalah optimasi desain turbin spiral Archimedes. Selain itu saya juga sedang aktif menjadi asisten kelas metode numerik dan meberikan pelatihan simulasi CFD . Materi dari kelas metode numerik dapat dilihat pada page dibawah ini:

PYTHON - Kelas Metode Numerik

CFDSOF-NG

Study dan Penelitian

Untuk menunjang penelitian yang saya lakukan di perkuliahan magister teknik mesin, saya melakukan beberapa study, diantaranya seperti Penggunaan Python untuk aplikasi metode numerik, kemudian mendalami kembali persamaan-persamaan dasar mekanika fluida, optimasi, dan sebagainya. Selama perkuliahan magister ini, rencanya semua materi-materi yang dipelajari akan dimuat di wiki ini. Sehingga, diharapkan dapat terdokumentasi dengan baik.

Turbin Archimedes

Publikasi Ilmiah

Saat ini, saya sudah menghasilkan beberapa publikasi ilmiah selama saya menjalani studi saya di S1 teknik mesin Universitas Indonesia. Untuk inofrmasi lebih lanjut, dapat dikunjugi laman berikut : Publikasi ilmiah

CATATAN PERKULIAHAN

Alhamdulillah segala puji bagi Allah subhanahu wata’ala, atas nikmat dan karunia-Nya, saya bisa kembali menulis dan memperbaharui tulisan saya di wiki ini. Shalawat serta salam senanatiasa di panjatkan kepada nabi akhir zaman, nabi kita tercinta, yang dengan perjuangan beliau, kita sekarang bisa merasakn terangnya ilmu, sehingga kita bisa terhindar dari kebodohan.

Alhamdulillah, sekarang saya sedang menjalani perkuliahan S2 di teknik mesin Universitas Indonesia dan, atas nikmat dan karunia Allah subhana hu wata’ala, saya bisa mendapatkan beasiswa. Sampailah saya di salah satu mata kuliah yang diampu oleh dosen yang sudah saya kenal sangat dekat, bahkan menjadi pembimbing saya di perkuliahan, yaitu Dr. Ir. Ahmad Indra Siswantara, atau yang akrab disapa dengan pak DAI. Sudah menjadi ciri khas beliau bahwa setiap mahasiswa yang hadir didalam mata kuliah nya, didorong untuk senantiasa mendokementasikan hasil kegiatan belajar mereka di dalam sebuah tulisan yang nantinya akan di muat pada laman wiki ini. Sehingga, setiap mahasiswa diharapkan dapat saling berbagi pendapat dan pengetahuan. Selain itu, hasil pembelajaran selama satu semester juga diharapkan dapat menjadi bahan belajar yang bermanfaat bagi orang lain.

KOMPUTASI TEKNIK

--pertemuan-1 : 03-02-2020--

Di pertemuan pertama di hari perkuliahan, beliau menyampaikan tujuan mempelajari komputasi teknik. Dari yang saya catat dan saya pahami, tujuan mempelajari komputasi teknik yang pertama adalah memahami konsep-konsep dan prinsip-prinsip didalam pelajaran komputasi teknik, yang mencakup sebagai berikut:

-Komputasi teknik : suatu kegiatan operasi aritmetik (tambah, kali, bagi, kurang) angka angka tadi.

-Kalkulasi enginering menggunakan komputer.

-Didalam istilah-isitlah komputasi teknik, banyak konsep-konsep yang harus dipahami. Pertama, konsep iterasi, kemudian, konsep error. Error sendiri terdiri dari beberapa jenis, ada residual error, dll. Jadi ada sebuah batasan error. Kemudian ada konsep convergen, konsep verifikasi dan validasi serta perbedaan keduanya.

-Metode-metode untuk mengolah data, misalnya untuk mengolah data seperti regresi, dan lain-lain.

-Contoh aplikasi metode numerik, misalnya memperkirakan persebaran temperatur ada sebuah plat dengan sebuah persamaan yang dimodelkan dengan :

2T1 + 3T2 + T3 = 5T4 5T1 - 2T2 + 5T3 = 7T4

-pada masalah-masalah engineering, terdapat banyak persamaan-persamaan model matematis yang harus diselesaikan, msialnya menyelesaikan sistem persamaan dengan menggunakan matrix yang dapat di selesaikan dengan komputer.

Lalu, tujuan mempejari komputasi teknik yang kedua adalah dapat memahamkan konsep-konsep disebutkan pada point 1 untuk aplikasi teknik mesin. Hal ini menruut saya sangat penting. Karena kita berharap bahwa ilmu yang akan kita pelajari ini nantinya menjadi ilmu yang bermanfaat dan dapat diamalkan. Sebagaimana nasihat emas dari Al- Imam Asy-Syafi’i Rahimahullah :

“Ilmu adalah yang bermanfaat dan bukan hanya dihafalkan” (Siyar A’lamin Nubala, 10: 89).

baca tulisan lengkapnya di Rumaysho: [1]

*Qadarallah, pada pertemuan ke 2 hingga ke 4, saya berhalangan hadir

Tugas Susulan

Pengertian Analisa Kata analisa dapat diambil pengertiannya dari kamus besar bahasa Indonesia, yaitu dari kata analisis yang didefinisikan sebagai penyelidikan terhadap suatu peristiwa (karangan, perbuatan, dan sebagainya) untuk mengetahui keadaan yang sebenarnya (sebab-musabab, duduk perkaranya, dan sebagainya). Namun, didalam bidang teknik, beberapa rekan dari kelas komputasi teknik juga memberikan definisi yang berbeda-beda, diantaranya adalah sebagai berikut: 1. Ilham Bagus waranto : pemecahan suatu masalah yang kompleks sehingga menjadi lebih mudah dipahami 2. Adzana Moslem : aktivitas yang dilakukan untuk mengurangi suatu permasalahan atau kasus 3. Evi Elisha : pemahaman atau pengkajian lebih dalamakan suatu hal. 4. Muchalis : suatu proses untuk menyelesaikan suatu masalah dan menghasilkan kesimuplan. 5. Ahmad Zikri : suatu penyilidikan terhadap persitiwa untuk mengetahui suatu kebenaran.

Demikian, analisa menurut pandangan saya adalah  : Sebuah usaha untuk menilai dan mengamati suatu permasalahan berdasarkan pemahaman yang dimiliki untuk menghasilkan sebuah kesimpulan atau dugaan

Catatan Ringkasan Computational Fluid Dynamics

1. Pendahuluan

Awal mulanya, CFD digunakan terbatas hanya pada aplikasi keteknikan berteknologi tinggi di aeronotika dan astronotika.

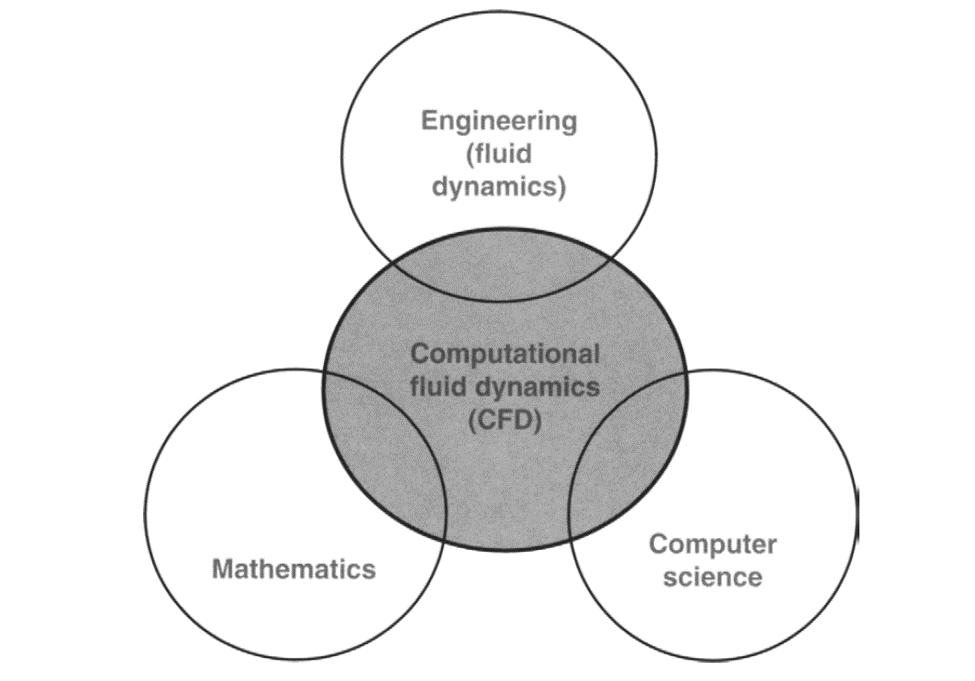
-> CFD merupakan cabang disiplin ilmu yang mengintegrasikan mekanika fluida, matematika, dan ilmu computer. Mekanika fluida, mempelejari fluida yang bererak maupun diam, serta pengaruh perilaku aliran terhadapa perpindahan panas dan reaksi kimia seperti pada pembakaran.

-> Lalu, karakteristik fisk dari gerak fluida tersebut dapat di deskripsikan melalui persamaan matematika dasar, umumnya merupakan bentuk persaaan partial differential yang mengatur proses tersebut dan biasanya disebut dengan governing equation.

-> untuk menyelesaikan governing equation tersebut, ilmuwan di bidang ilmu komputer menggunakan bahasa pemrograman tingkat tinggi untuk menyelesaikannya, dan kemudian menjadikannya sebuah program atau software. Secara sederhana, makna computational pada CFD berarti study mengenai aliran fluida melalui simulasi numerik, yang mana melibatkan pemanfaatan software pada komputer.

-> Pertanyaannya, apakah kita memerlukan orang-orang dari 3 disiplin ilmu tersebut secara spesifik. Jawabannya adalah tidak, karena orang yang mahir dalam mempelajari ilmu CFD ini justru akan mendapatkan ilmu-ilmu yang ada di 3 disiplin ilmu tersebut.

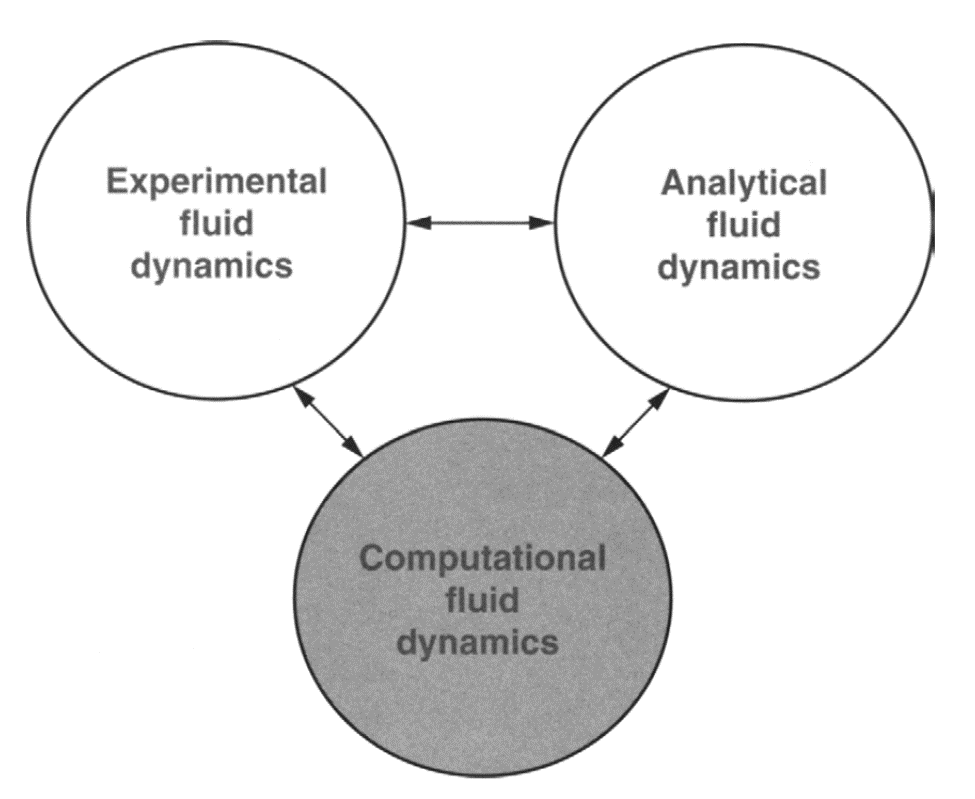
-> CFD menjadi salah satu dari 3 cara untuk solusi dari suatu masalah pada fluid dynamic and heat transfer. Dan 3 cara tersebut saling berkaitan dan tidak saling terpisah/terisolasi, yaitu analytical, experimental, dan numerical computational.

-> saat dahulu, orang-orang yang mendalami ilmu CFD akan menyisihkan waktu mereka untuk menulis code program computer mereka sendiri. Namun demikian, dengan semakin bertambahnya permintaan dari Industri dan bahkan juga di dalam akademis yang menginginkan pengetahuan mengenai CFD dengan waktu yang singkat (tidak terlalu lama), maka tidak asing lagi bahwa orang-orang mulai banyak yang mengabaikan untuk menulis code programnya masing-masing, terlebih lagi dengan meningkatnya penggunaan software CFD secara commercial yang tersedia. Multi purpose software CFD mulai banyak di terima secara luas, terutama karena model-model yang telah berkembang dan dapat merangkum fenomena aliran fluida secara fisik. Selain itu, penulisan code program CFD sudah banyak dilakukan dan di uji dengan pihak-pihak pengembang software tersebut, maka di saat ini, pengguna CFD tidak lagi menghadapi persoalan-persoalan semacam itu, karena program-program yang telah berkembang saat ini dapat digunakan untuk berbagai persoalan aliran fluida.

-> Akan tetapi, CFD bukanlah semata-mata hanya mahir dalam menggunakan software dan semacamnya. Hal yang penting dalam mempelejari ilmu CFD (khususnya yang akan disediakan buku ini) adalah mempelajari ilmu CFD secara lebih bijakssana, yaitu memberikan pemahaman mengenai pokok konsep dasar dan mengetahui "Know-How" (atau alasan-alasan) untuk menangani masalah masalah aliran fluida.

-> beberapa referensi bagi yang ingin mendalami atau melakukan riset mengani pengembangan model matematika dapat melihat buku-buku seperti (Fletcher,1991, Anderson, 1995, Versteeg dan Malalakasera,1995).

CFD Technique

-> Secara umum, terdapat teknik dasar komputasi yang digunakan untuk mencari solusi dari governing equation dari permasalahan fluid dynamic dengan boundary condition yang tepat sesuai dengan kasus spesifik tersebut. ->Proses untuk mendapatkan solusi komputasi (computational solution) terdiri dari 2 tahap. Tahap pertama yaitu meliputi konversi persamaan diferensial parsial dan auxiliary(boundary and initial) condition menjadi sebuah sistem persamaan linier aljabar diskrit (system of discrete algebraic equations). Langkah ini disebut dengan langkah diskritisasi (discretization stage). -> Pada bab sebelumnya, telah dibahas bagaimana menyelesaikan persamaan governing equation secara analytical. Namun pada kondisi realnya, kondisi aliran adalah 3 dimensi. Sehingga penyelesaiannya sangat kompleks dan tidak mudah. Bahkan, walaupun aliran disederhanakan disederhanakan menjadi aliran 2 dimensi, governing equation akan tetap diselesaikan secara analitik.

-> Oleh karena itu, dari pada menyelesaikan persamaan governing equation dan mendapatkan nilai parameter-parameter simulasi seperti u,v,w,p, dll yang diselesaikan dengan sebuah fungsi eksplisit tertutup (closed-form expression), kita dapat mendapatkan nilai dari parameter-parameter tersebut pada lokasi-lokasi diskrit (lokasi-lokasi yang telah terdiskritisasi) di dalam domain aliran fluida dengan menggunakan CFD solver dan persamaan original dari Navier-Stokes di aproksimasi dengan menggunakan turunan aljabar. Persamaan-persamaan differential partial tersebut, secara keseluruhan di ganti dengan (replace) sebuah sistem persamaan aljabar, dan digunakan untuk menyelesaikan nilai diskrit dari variable pada medan aliran. Persamaan original differential parsial akan di diskritisasi dengan tujuan agar didapatkan nilai solusi pada titik-titik atau lokasi-lokasi yang diskrit.

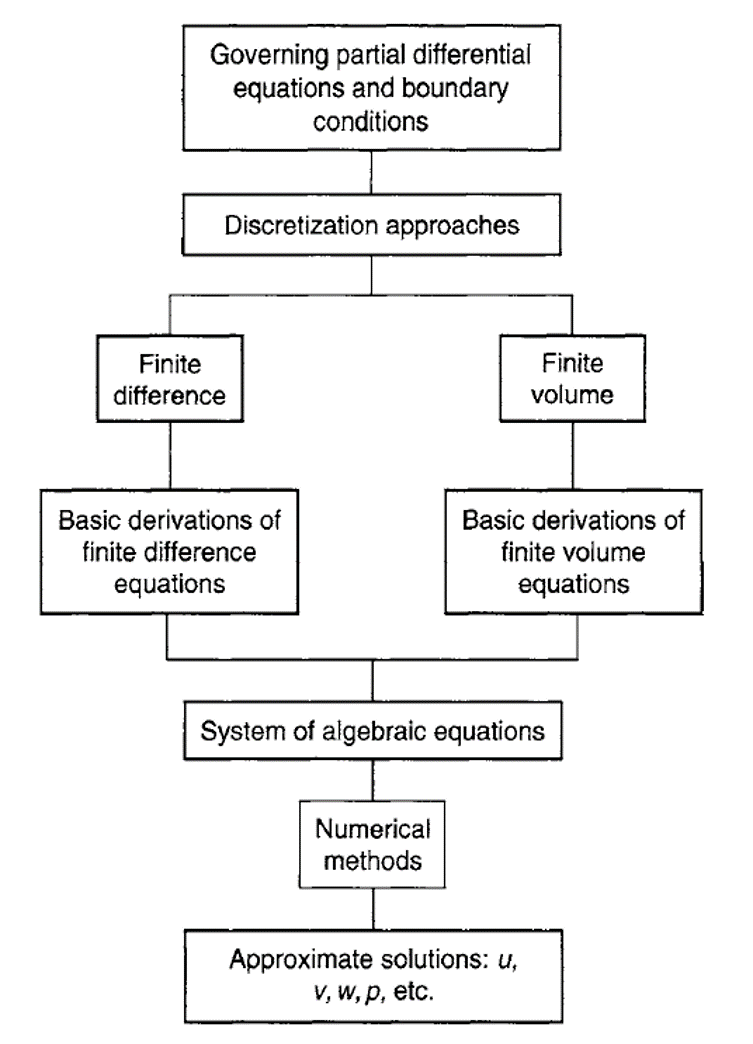
-> Pendekatan diskritisasi yang paling utama dan masih digunakan hingga saat ini adalah metode finite difference dan finite volume. Berikut proses prosedur untuk mendapatkan sebuah solusi komputasi :

-> Metode finite difference memiliki kesamaan dengan finite volume. Yang membedakan keduanya adalah dimana finite difference menggunakan fungsi polinomial yang sederhana pada elemen lokalnya untuk mendeskripsikan variasi dari variabel aliran yang tidak diketahui.

->Metode ini tidak banyak digunakan pada aplikasi CFD, walaupun telah ada program commercial dan research code nya. Hal ini karena metode diskritisasi ini membutuhkan computational resources dan daya komputasi komputer yang lebih tinggi dari pada metode finite volume.

-> Namun demikian, finite difference baik untuk dipelajari karena metode tersebut mebentuk dasar (foundation) secara comprehending(?) esensi dari dari diskritisasi(?).

-> Saat ini, CFD hampir semuanya menggunakan metode diskritisasi finite volume method. Hal ini karena kemampuannya yang dapat diaplikasikan pada structured mesh maupun unstructured mesh. Sehingga metode ini cukup populer dan dapat mengatasi kasus-kasus dengan bentuk geometri yang bermacam-macam.

a. Finite Difference Method

-> Langkah pertama dalam merepresentasikan persamaan differential parsial pada finite difference adalah dengan menggunakan ekspansi deret Taylor

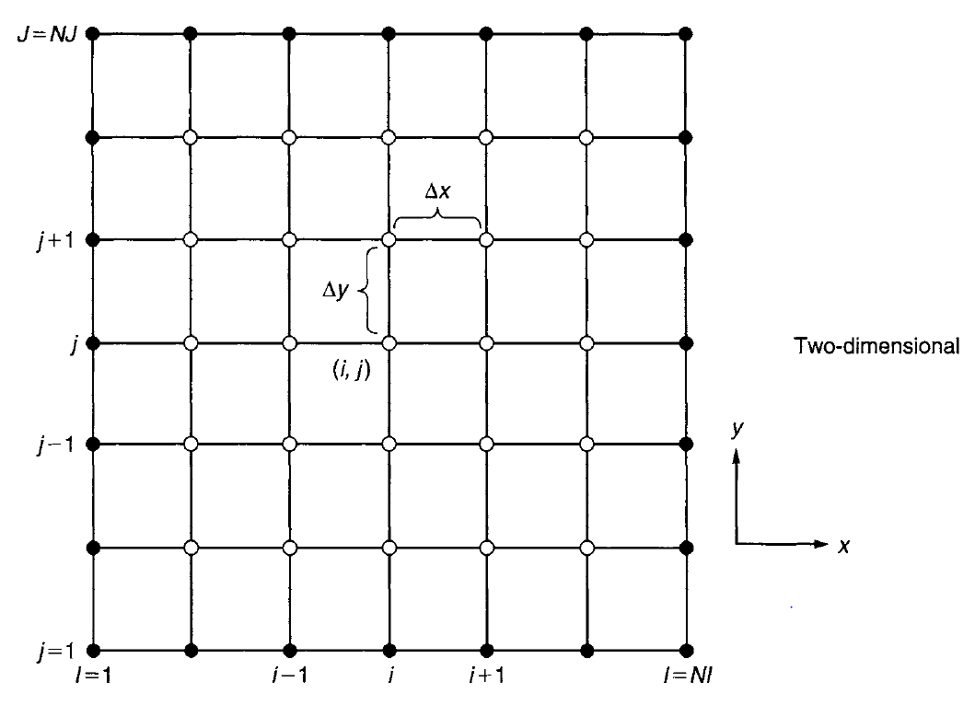Gambar 1 Nodes tertutup (hitam) menandakan nodes boundary, dan nodes terbuka (nodes transparan) menunjukkan nodes yang akan dikalkulasi secara numerik

Untuk contoh pada gambar 1, maka misalkan ada sebuah variable generic dari aliran (ɸ) pada nodes (i,j), maka dengan menggunakan deret taylor expansion pada nodes i+1 dan i-1, didapatkan sebagai berikut :

Dengan syarat bahwa nilai deret tersebut akan convergence apabila ∆X0 Dengan mengurangi kedua persamaan diatas, maka didapatkanlah persamaan sebagai berikut:

atau

Dimana truncation error adalah error akibat pemotongan deret Taylor. Oleh karena itu, dapat dipahami bahwa akurasi dari hasil kalkulasi dipengaruhi oleh ukuran dari ∆X. Oleh karena itu, semakin kecil nilai ∆X, maka akurasinya akan semakin baik. Persamaan di atas merupakan persamaan central difference, di mana dibutuhkan dua nilai nodes, yaitu nodes setelah dan sebelum nodes yang akan dicari. Dapat dilihat juga bahwa persamaan tersebut memiliki keakuratan berderajat second order polynomial (dilihat dari truncation error).

Selain itu, perhitungan juga dapat dilakukan dengan menggunakan approksimasi dengan derajat polynomial orde 1, sebagai berikut:

Pada persamaan forward difference, dibutuhkan nilai nodes setelah nodes yang akan dicari, sedangkan pada backward difference, dibutuhkan nilai nodes sebelumnya dari nilai nodes yang akan dicari. Namun demikian, kedua persamaan ini memiliki keakuratan dengan derajat first order polynomial, sehingga kedua persamaan ini tidak lebih akurat dari persamaan central difference. Hal ini juga menunjukkan bahwa apabila grid di refine (jarak antar nodes diperkecil dan jumlah nodes semakin banyak) maka akan meningkatkan akurasi dari hasil perhitungan.

Penggunaan deret taylor expansion juga dapat digunakan untuk persamaan differential parsial order 2 untuk central difference, dengan langkah yang sama ketika menggunakannya untuk persamaan differential order 1, dengan persamaan sebagai berikut:

Selain melakukan diskritisasi terhadap ruang, penggunaan deret Taylor juga dapat digunakan terhadap waktu. Sehingga, misalnya untuk persamaan forward difference terhadap waktu ditunjukan sebagai berikut:

b. Finite Volume

o Metode finite volume mendiskritisasi bentuk integral dari persamaan konservasi (integral form of the conservation equations) pada ruang (physical space) secara langsung.

o Jadi, domain komputasi akan dibagi menjadi sejumlah control volume yang berdekatan (bahkan mugnkin berdempetan).

o Di bagian tengah dari tiap volume tersebut, nilai variable-variable aliran dihitung. Interpolasi digunakan untuk menghitung nilai variable di permukaan pada control volume, berdasarkan nilai di bagian tengah volume dan rumus quadrature (?) diaplikasikan untuk mengaproksimasi integral permukaan dan volume

o Metode finite volume bekerja pada control volume, bukan pada titik perpotongan antara garis grid, sebagaimana pada metode finite difference, sehingga metode finite volume ini dapat digunakan untuk menyelesaikan berbagai bentuk dan jenis grid. Sehingga, daripada menggunakan grid beraturan (strucutred grid), grid tidak beraturan (unstrucutrued grid) dapat digunakan untuk berbagai bentuk geometri dan lokasi dari control volume.

o Karena grid pada metode finite volume hanya mendefinisikan batasan dari control volumenya, aka metode finite volume ini memanfaatkan metode konservasi, sepanjang integral permukaan yang diaplikasikan pada pada batasan-batasan control volume tersebut sama dengan control volume yang di sharing (digunakan juga) untuk boundary tersebut (?).

o Satu kekurangan dari metode ini dibandingkan dengan metode finnite difference adalah approksimasi differensiasi (?) yang membutuhkan order yang lebih tinggi dari order dua yang mana lebih sulit untuk dikembangkan pada 3 dimensi. Hal ini karena dibutuhkan dua tingkat aproksimasi, yaitu interpolasi dan integrasi.

o Namun demikian, finitoe volume memili lebih banyak keunggulan dibandingkan dengan kekurangannya. Misalnya, salah satu fitur penting dari metode finite volume adalah mesh tipe “finite-element” yang dapat digunakan, yang mana mesh dapat dibentuk oleh kombinasi dari bentuk triangle dan quadrilaterals pada kasus dua dimensi, atau dalam bentuk tetrahedra dan hexahedra pada kasus tiga dimensi. Mesh tipe unstructured atau tidak beraturan ini memberikan tingkat fleksibiltas yang lebih baik untuk dapat menangani geometri-gemetri yang kompleks. Fitur lainnya yang menarik dari metode finite volume adalah tidak dibtuhkan transformasi dari persamaan-persamaan yang berkaitan dengan boddy-fitted coordinat system(?) dimana pada metode finite difference diperlukan transformasi.

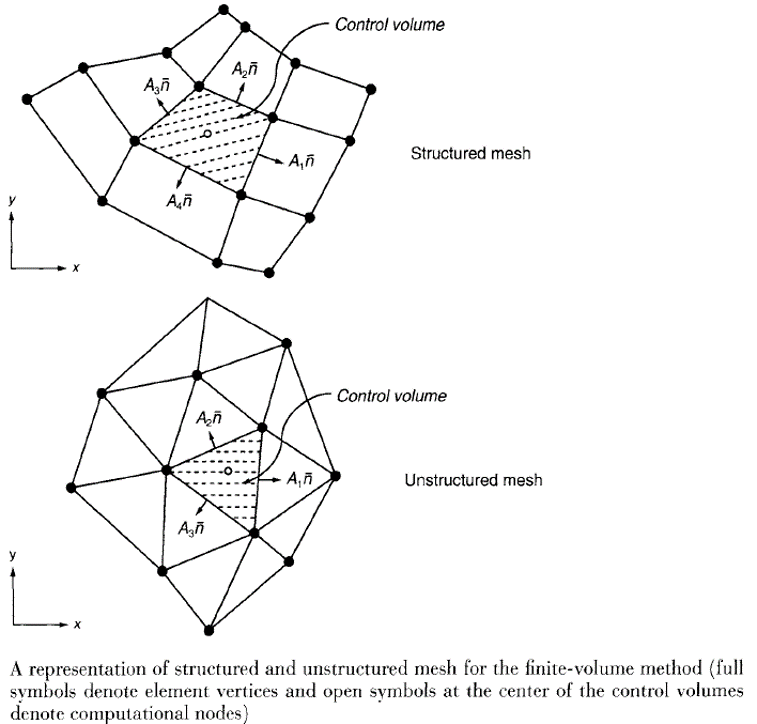
o Sebagai ilustrasi, dapat dilihat grid structured ataupun unstructured yang digunakan pada metode finite volume:

o Landasan dasar dari metode finite volume ini adalah integrasi volume (Volume Integration, yang nantinya akan memanfaatkan konsep teorema gauss).

o Di dalam sebuah control volume yang akan dikalkulasi, area permukaan batas pada element tersebut (yang akan dikalkulasi) akan secara langsung terhubung dengan turunan orde pertama dan order kedua dari variable generic medan aliran (ɸ) yang terdiskritisasi. Area permukaan pada arah normal terhadap permukaan volume sebagaimana di tunjukan pada gambar di atas diselesaikan dengan terkait terhadap arah koordinat cartesian terhadap area yang terproyeksi (Axi) dan (Ayi) pada arah x dan y secara berturut-turut. Area yang terproyeksi tersebut akan bernilai positif apabila vector outward (vektor yang mengarah keluar dari volume control) memiliki arah yang sama dengan sistem koordinat cartesian. Sebaliknya, maka akan bernilai negatif.

o Kemudian, dengan mengaplikasikan teorema Gauss Divergence pada integral volume, turunan pertama dari ɸ pada kondisi dua dimensi, sebagai contoh, terhadap arah x, direpresentasikan dengan approksimasi sebagai berikut:

Di mana ɸ1 adalah nilai variabel pada permukaan dai element finite volume dan N dinotasikan sebagai jumlah permukaan batas pada element volume. Persamaan di atas diaplikasikan pada tipe finite volume apapun yang dapat direpresentasikan di dalam grid numerical. Untuk grid element quadrilateral pada dua dimensi untuk structured mesh sebagaimana di tunjukan pada gambar di atas, nilai N adalah 4 karena pada elemen finite volume tersebut, terdapat 4 permukaan batas. Pada kasus tiga dimensi, untuk element hexagonal, nilai N berjumlah 6.

--pertemuan 05 04/03/2020--

- Kelas komputasi teknik pada pertemuan kali ini adalah membahas skripsi atau tugas akhir dari saudara Syefudin Ichwan. Topik skripsi tersebut membahas tentang pengukuran laju erosi pada sebuah sample pipa SS 304 dengan menggunakan alat bernama Siklotron, yang mengaktifkan material SS 304 sehingga bersifat radio aktif. Hal ini sebagaimana terdapat pada wiki page beliau di lama berikut : S.Ichwan. Yang saya pahami, skripsi beliau bertujuan untuk mengetahui laju korosi agar nantinya kondisi pipa tersebut dapat di prediksi ketahanan dan umurnya, sesuai dengan aplikasi atau material fluida yang ada di dalamnya.

- Kemudian diskusi berlanjut, dimana saudara Ichwan menjelaskan bagaimana cara mengetahui laju korosi tersebut. Beliau mengetakan bahwa laju korosi dapat dipredeksi dengan mengukur partikel SS 304 yang teraktivasi menjadi sebuah radio aktif, yang di representasikan sebagai hasil dari adanya Korosi. Kemudian, nantinya hasil dari pengukuran tersebut akan dimasukan kedalam sebuah persamaan.

- Kemudian, diskusi berlanjut dengan menyederhanakan pembahasan mengenai erosi (pengikisan) dan apa pengaruh massa jenis terhadap erosi. Beberapa teman berpendapat bahwa semakin besar densitas, maka erosi akan semakin besar, karena fluida semakin berat dan gesekan fluida terhadpa dinding semakin besar. Lalu beberapa rekan yang lain mengatakan bahwa hal itu tidak valid, karena tidak semua fluida yang memiliki densitas yang lebih besar akan mengakibatkan tegangan geser yang lebih besar. Contoh misalnya minyak, yang memiliki viskositas yang lebih rendah, namun akan menghasilkan tegangan geser terhadap dinding yang lebih tinggi dari pada air. Sehingga, ada faktor lain yang mempengaruhi geseran terhadap dinding, yaitu viskositas dari fluida tersebut.

Optimasi Kebutuhan Energi Manusia

- Untuk menghitung kebutuhan kalori yang dibutuhkan untuk aktivitas sehari-hari, saya menggunakan cara yang ditulis pada lama wiki page milik Evi Elisa Ambarita dengan detail perhitungan sebagai berikut:

ebelum menghitung, kita harus mengetahui terlebih dahulu tinggi badan (TB) dalam sentimenter dan Berat Badan Ideal (BBI) dengan rumus sebagai berikut:

BBI = (TB-100) – (10% x (TB – 100))

Selanjutnya, kita dapat hitung Kebutuhan Kalori Basal (KKB) atau Basal Metabolic Rate (BMR). KKB merupakan kebutuhan kalori yang dibutuhkan oleh tubuh untuk metabolisme basal, yakni metabolisme yang wajib dilakukan mahluk hidup walaupun tidak membutuhkan energi. Ini berarti metabolisme tubuh akan tetap berjalan meskipun dalam keadaan tidur atau tidak melakukan apa-apa. Beriku adalah rumus menghitung angka KKB:

KKB Laki-laki = 30 kkal x BBI

KKB Perempuan = 25 kkal x BBI

Menghitung Kebutuhan Kalori Total (KKT)

Kebutuhan kalori total adalah jumlah kebutuhan kalori tubuh ditambah dengan jumlah kalori saat melakukan aktivitas fisik. Kita mengenal tiga jenis aktivitas, yaitu :

1. Aktivitas ringan seperti membaca (10%), menyetir mobil (10%), kerja kantoran (10%), mengajar (20%), berjalan (20%).

2. Aktivitas sedang: kerja rumah tangga (20%), jalan cepat (30%), bersepeda (30%).

3. Aktivitas berat: aerobik (40%), mendaki (40%), dan jogging (40%)

Rumus KKT = KKB + Aktivitas Fisik

contoh perhitungan:

Tingi badan saya adalah 173 cm. Sehingga berat badan idela saya (BBI) :

BBI = (173-100) – (10% x (173 – 100)) = 65,7 kg

Kemudian, nilai KKB dihitung sebagai berikut:

KKB = 30kkal x 65,7 = 1971 kkal

pada hari senin, 02/03/2020, aktivitas saya dirincikan sebagai berikut:

1. Berangkat ke kampus dengan menggunakan motor (Aktivitas ringan): persentase 10%

2. Mengikuti 3 kelas perkuliahan (Aktivitas ringan): persentase 10%

3. Berjalan di sekitar kampus (Aktivitas sedang) : 20%

sehingga, dengan rumus KKT, dapat dihitung kebutuhan kalori total sebagai berikut:

KKT = 1971 kkal + (10% x 1971 kkal) + (10% x 1971 kkal) + (20% x 1971 kkal)

KKT = 3154 kkal

- Transportasi, dengan menggunakan motor. Estimasi dengan menggunakan motor honda revo, perjalanan dari tempat tinggal ke kampus adalah sejauh kurang lebih 20 KM. Konsumsi bahan bakar untuk motor saya untuk setiap perjalanan pulang-pergi diestimasi menghabiskan 1,3 liter, atau setara dengan Rp10.000,-. Berdasarkan nilai kalori bahan bakar bensin secara umum 8240 kcal/liter, maka jumlah energi yang dibtuhkan untuk transportasi menjadi

o 1,3 liter x 8.240 kcal/liter x 4,184 kJ/kcal = 44.819 kJ

- Konsumsi laptop yang saya gunakan, dengan asumsi hari senin , saya hanya menggunakan laptop selama 4 jam. Sehingga, dengan menggunakan power calculator, sesuai dengan spefikiasi laptop yang digunakan, didapatkan konsumsi energi nya sebesar.

o 261 Watt X 4 jam X 3600 = 3.758,4 kJ

-Estimasi penggunaan Handphone.Rata-rata daya melakukan pengisai ulang handphone saya 1 kali dalam sehari. Sehingga, didalam sehari, saya menghabiskan seluruh energi yang ada di handphone saya. Handphone yang saya gunakan adalah Samsung tipe A20. Untuk mengukur konsumsi energi listrik dari handphone, saya menggunakan aplikasi bernama Ampere yang dapat mengukur tegangan dan kapasitas baterai Handphone. Didapati bahwa voltase rata-rata baterai handphone saya sebesar 3,7 Volt dengan kapasitas baterai 3900mAh. Sehingga, estimasi energi yang dikonsumsi oleh handphone saya adalah:

o Estimasi = 3.900mAh * 3,7 Volt * 3600 sekon/hour * 1/1000 A/mA * 24 hour = 1.246,75 kJ

- Sehingga, estimasi total konsumsi energi hari senin tanggal 02/03/2020 adalah

o Estimasi = 44.819 kJ + 8.368 kJ + 3.758,4 kJ + 1.246,75 kJ = 58.192,3 kJ

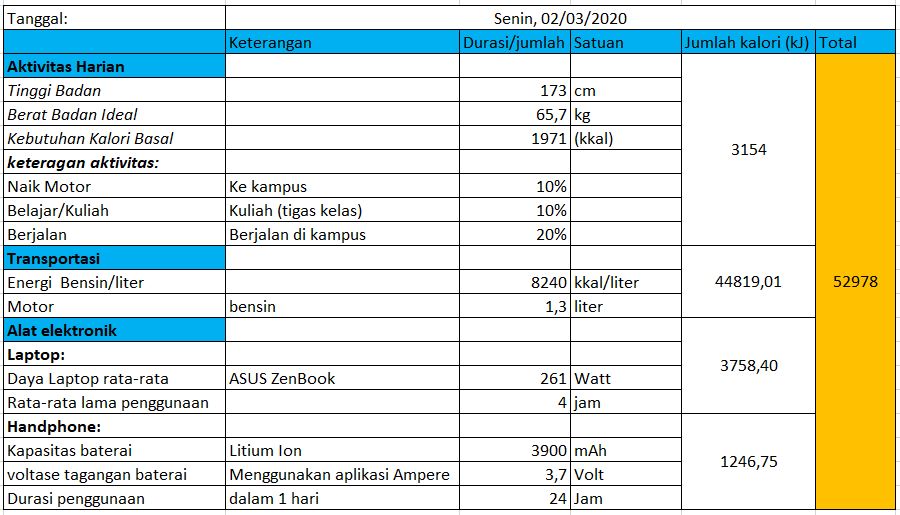
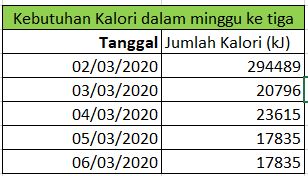
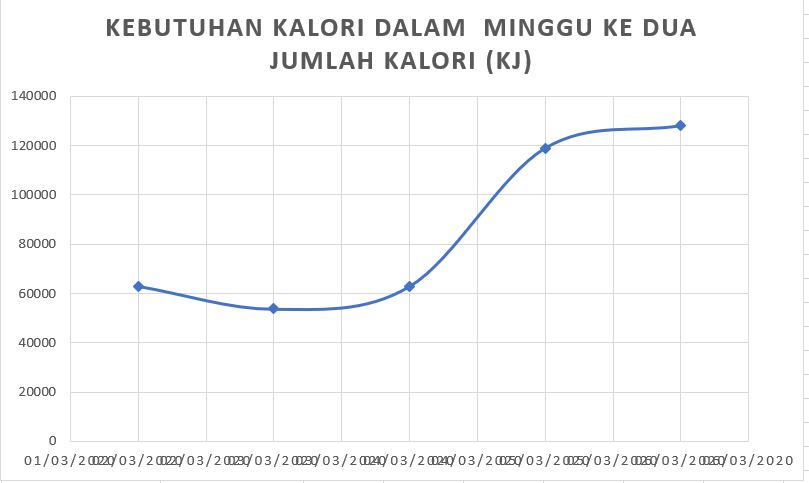
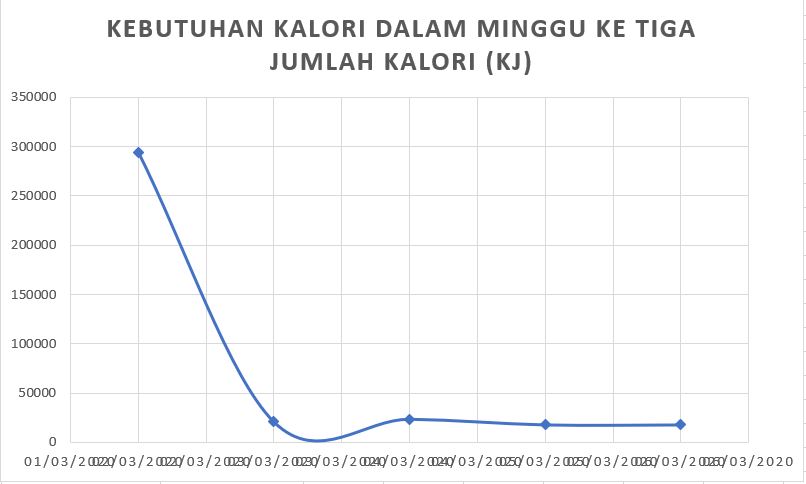
Perhitungan di atas dilakukan selanjutnya dilakukan dengan menggunakan Ms. Excel, dan diberikan melalui tabel berikut:

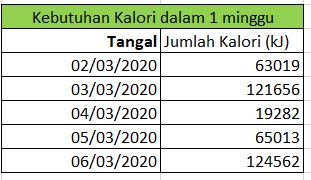
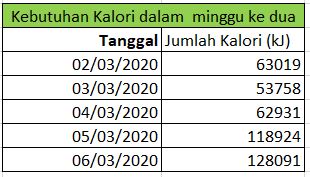
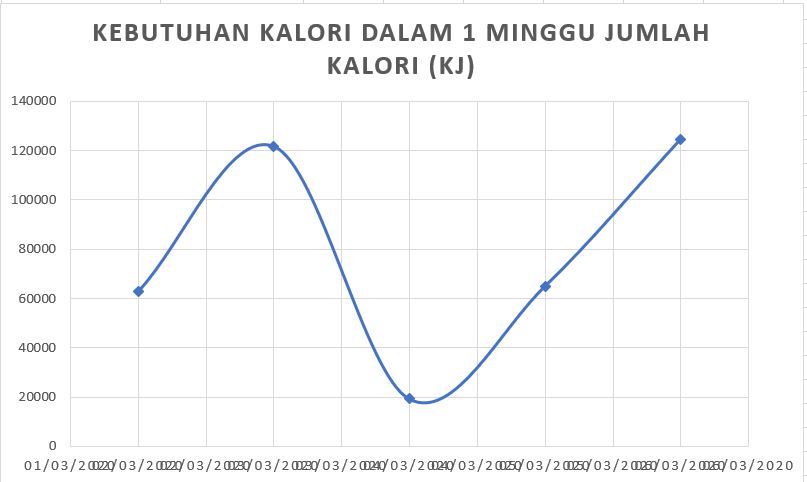
perhitungan dengan Ms.excel tersebut digunakan untuk menghitung jumlah konsumsi energi di hari-hari berikutnya. Sehingga, selama 1 minggu didapatkan hasil data sebagai berikut:

Fungsi Objective :

->Bagaimana mendapatkan penggunaan energi yang optimum?

Membuat fungsi matematis dari penggunaan energi

Total Energi = Aktivitas Harian + Kebutuhan Transportasi + (Kebutuhan Laptop + Kebutuhan Handphone)

Jika dirinci, maka masing-masing dari kebutuhan tersebut dapat dijabarkan melalui model matematis sebagai berikut:

->Aktivitas harian ; karena aktivitas harian sangat dipengaruhi oleh bilang variabel yang sangat tidak menentu nilainya (tergantung agenda dan agak sulit menentukan variabel bebas dan variabel terikatnya) maka nilai aktivitas harian hanya berupa sebuah nilai konstanta yang didapat dengan merata-ratakan jumlah kebutuhan energi berdasarkan aktivitas harian selama 3 minggu sebelum UTS.

->Kebutuhan Transportasi = jumlah naik mobil/minggu x konsumsi bahan bakar +jumlah naik motor x konsumsi bahan bakar motor

K_trans = (n_mobil x 3 liter x 34476,16 kJ/liter)+ (n_motor x 1,3 liter x 34476,16 kJ/liter)

Kebutuhan penggunaan Laptop :

K_laptop= lama penggunaan x daya laptop

K_laptop = t_laptop x 261 Watt

Kebutuhan Penggunaan Handphone

K_HP= lama penggunaan x daya handphone

K_HP= t_HP x 51,95 kJ/jam

Maka Kebutuhan Kalori total yang menjadi fungsi objective dari optimasi adalah:

K_Total=(n_mobil x 3 liter x 34476,16 kJ/liter)+n_motor 1,3 / liter x 34476,16 kJ/liter)+t_laptop x 3600 x 261Watt/1000 + t_HP x 51,95 kJ/ jam

Dari persamaan fungsi objective yang dibangun, terdapat 4 variable yang harus dicari untuk mendapatkan nilai konsumsi energi total yang paling rendah untuk aktivitas per minggu nya. Namun demikian, terdapat beberapa constraint atau nilai batasan yang harus dipenuhi sebagai berikut:

Jumlah pulang pergi dari rumah ke kosan minimal 2 kali, sehingga, minimal ada 4 kali perjalanan dari rumah hingga ke kampus dalam 1 minggu.

Dalam sehari, minimal membutuhkan laptop minimal 4 jam dinyalakan karena kebutuhan untuk mengerjakan tugas dan melanjutkan simulasi. Namun, laptop juga hanya dibatasi untuk digunakan hanya maksimal 12 jam. Di satu sisi, handphone juga dibutuhkan untuk menggunakan WA untuk komunikasi. Namun, apabila laptop aktif, maka WA bisa melalui laptop dan handphone bisa di non aktifkan. Dalam sehari, rata-rata waktu yang digunakan untuk menggunakan WA minimal 8 Jam. Sehingga, dari kondisi batas tersebut, dapat dibuat constraint dan boundary sebagai berikut:

n_mobil + n_motor>>=4

t_laptop + t_Hp >= 8

Oleh karena itu, untuk mencari nilai yang memenuhi contraint diatas, dapat dilakukan sebuah Optimasi dengan menggunakan bantuan Python.

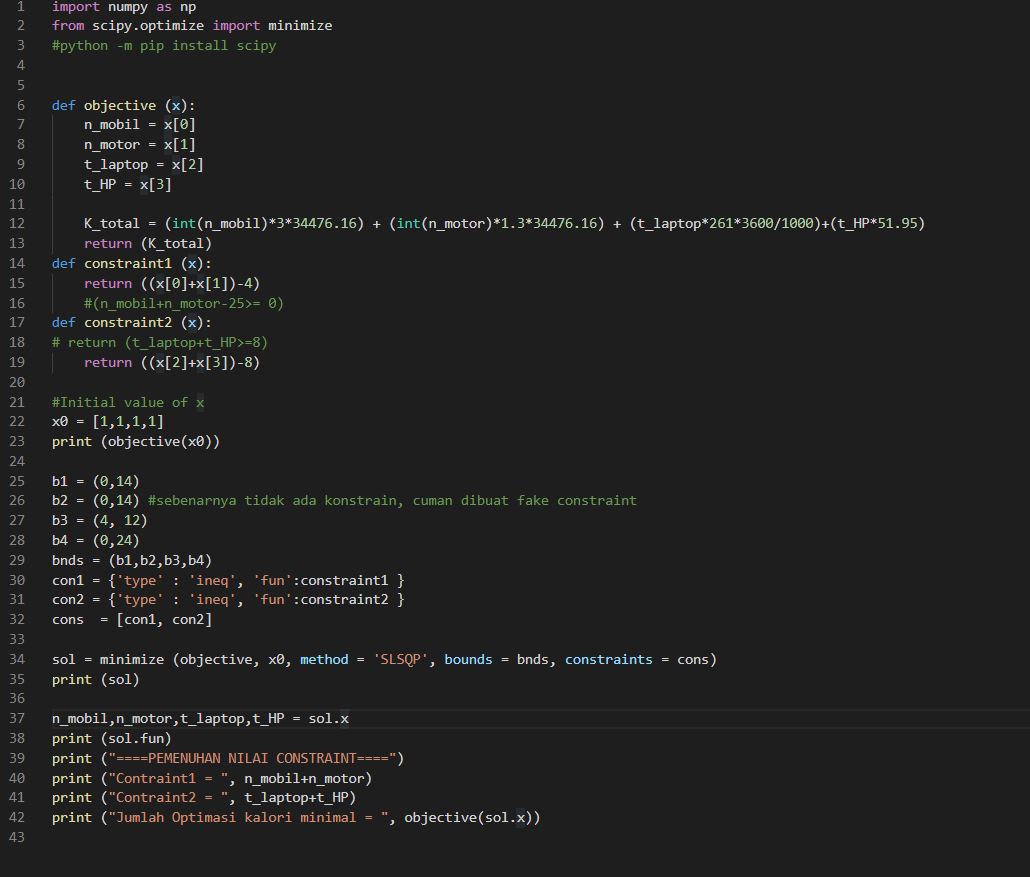
Code Python Yang Digunakan:

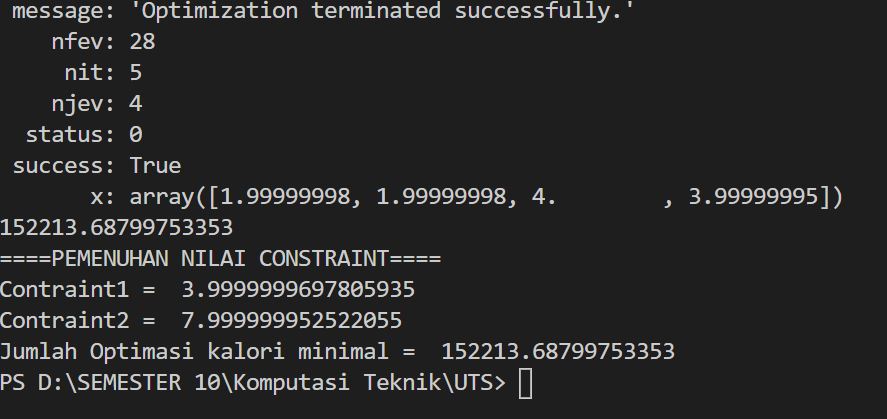
Dan Dihasilkan hasil sebagai berikut:

Sehingga didapatkan bahwa variable yang memenuhi adalah:

Jumlah penggunaan mobil (n_mobil) = 2

Jumlah penggunaan motor (n_motor) = 2

Durasi penggunaan laptop (t_laptop) = 4 Jam

Durasi_penggunaan HP (t_HP) = 4 Jam

Nilai Kalori Total Minimum nya : 152213 Kalori / Minggu

--pertemuan 09 04/03/2020--

Perkuliahan hari ini diasali dengan muhasabah atau evaluasi mengenai jalannya perkuliahan selama ini. Kemudian, muhasabar yang saya buat adalah sebagai berikut:

Topik diskusi di kelas:

Diskusi dimulai dengan sebuah kasus yang diberikan oleh Pak Indra, yaitu pengelaman beliau mengenai penyelesaian suatu masalah pada Feed water heater yang mengalami adanya kebocoran. Maka Pak Indra meminta komentar mahasiswa mengenai langkah awal apa yang harus diketahui. Saya menjawab bahwa langkah pertama yang perlu dilakukan pada kasus di atas adalah mengumpulkan informasi sebanyak banyaknya, baik melalui informasi dari pengguna atau user maupun melalui inspeksi lapangan secara langsung.

Hal penting dari diskusi yang dapat dipelajari

Rule of thumb untuk analisis Komputasi / Metode numerik terdiri dari beberapa langkah:

1. Initial Thinking - jadi, sebelum kita melakukan analisa pada sebuah masalah, kita harus memiliki gambaran awal mengenai masalah tersebut dan bagaimana cara atau langkah-langkah yang harus kita lakukan. -Misal di dalam sebuah tulisan karya ilmiah atau paper yang sedang kita kerjakan, di Intorduction, kita harus tau apa masalah yang sedang kita ingin selesaikan.

2. Menyusun Model Matematisnya, dimana model matematis ini mengandung asumsi asumsi yang kita lakukan. Yang menjadi catatan bahwa rumus-rumus yang tersedia saat ini hanya bersifat universal, sehingga model matematis yang ingin kita gunakan harus kita kembangkan dengan lebih spesifik sesuai dengan kasus spesifik yang kita kerjakan.

3. Membuat Model ,yaitu sebuah rumusan yang kita hitung. Model ini dibuat sesuai dengan initial thinking yang telah kita lakukan, dan berisi model atau persamaan matematis yang dibutuhkan. Model ini istilahnya adalah 'solve the right equation'

4. Simulasi: simulasi menurut pak dai adalah menjalankan model yang kita buat, atau mengeksekusi model yang kita buat. Adapun simulasi menurut saya pribadi adalah proses penyelesaian dari model yang telah dibuat untuk mendapatkan hasil atau gambaran berdasarkan model yang telah dibuat tersebut.

5. setelah itu kita lakukan verifikasi. Verifikasi ini dilakukan untuk memeriksa apakah model atau perhitungan yang kita lakukan ini terhindar dari kesalahan numerik.Atau istilahnya yaitu 'solve the equation right'.

6. Setelah itu kita melakukan validasi yang tujuannya adalah untuk menguji seberapa aktual hasil simulasi yang kita lakukan. Validasi dapat dilakukan dengan membandingkan hasil simulasi dengan teori yang ada, fenomena-fenomena yang berlaku secara umum, ataupun dengan menggunakan data sekunder seperti dari hasil uji experimental.

7. Setelah melakukan validasi, kita melakukan pembahasan dari hasil yang didapat, atau dikenal sebagai Result and Discussion. Di dalamnya berisi analisis mengenai hasil yang didapatkan.

UTS Komputasi Teknik

1. Video Materi Belajar selama 1/2 semester

QUIS 2 : Gerak Osilasi

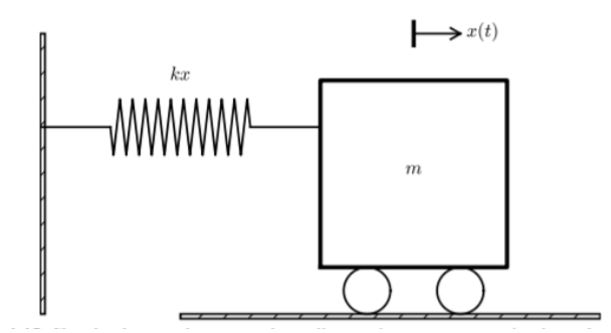
Pada Kuis kali ini, soal pada kasus osilasi sistem pegas sederhana sebagai berikut:

Pertama, sesuai dengan sifat naturalnya, ketika suatu pegas mengalami penyimpangan, maka pegas akan meberikan gaya reaksi berlawanan dengan arah simpangannya. Begitu pula apabila pada kondisi awalnya, pegas berada pada kondisi diam, namun berada pada posisi yang menyimpang sejauh X0 dari posisi setimbangnya hingga akhirnya pegas akan dilepas. Maka dapat diberikan sebuah model matematis, yaitu berupa persamaan differensial ode 2. Sebagai berikut:

Dimana nilai

Lalu, solusi exact untuk gerak osilasi adalah X= A.Cos(\omegat), dimana A adalah amplitudo, atau nilai simpangan pada keadaan awal. Untuk mendapatkan posisi X dari sistem pegas tersebut, pendekatan secara numerik juga dapat dilakukan. Pertama, pendekatan dapat dilakukan dengan menggunakan 2 metode numerik. Yang pertama adalah metode Forward-Euler Method. Sebagia berikut:

Metode kedua, yaitu metode Backward-Forward Euler, sebagai berikut:

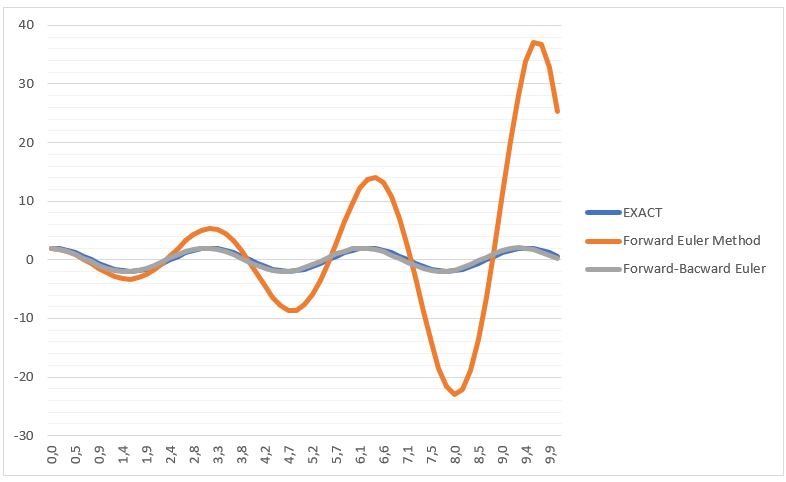
Pada kasus ini, diberikan nilai omega=2, nilai X0 =2, nilai ∆t=0,157. Kemudian, perhitungan dilakukan dengan menggunakan bantuan Ms. Excel dan diperoleh hasil perbandigan sebagai berikut:

Dapat dilihat pada grafik diatas, bahwa hasil perhitungan dari Forward Euler maupun Forward-Backward pada detik-detik awal osilasi masih relatif sama, namun ketika periode osilasi semakin panjang, dapat terlihat bahwa hasil perhitungan numerik metode Forward-Euler mengalami penyimpangan dari hasil solusi exact yang cukup jauh. Hal ini demikian karena error perhitugan yang dihasilkan dari metode Forward-Euler semakin tinggi. Hal berikut demikian karena pada metode Forward- Euler, amplitudo mengelami pertumbuhan nilai yang signifikan. Hal berikut demikian ddianalisa karena pada metodologi Forward-Euler ini, perhitungan dilakukan berdasarkan gradient atau nilai differensial di titik pada node waktu ke-n (node yang sedang dihitung) sedangkan persamaan differensial yang digunakan pada sistem pegas ini terdiri dari adanya laju perubahan kecepatan dari osilasi pegas itu sendiri (yaitu turunan orde 2 dari posisi X). Oleh karena itu, adanya error pada hasil perhitungan dari metode Forward-Euler dapat mengakibatkan pertumbuhan pada nilai Amplitudo dari osilasi tersebut, sehingga hasil perhitungan akan semakin menyimpang. 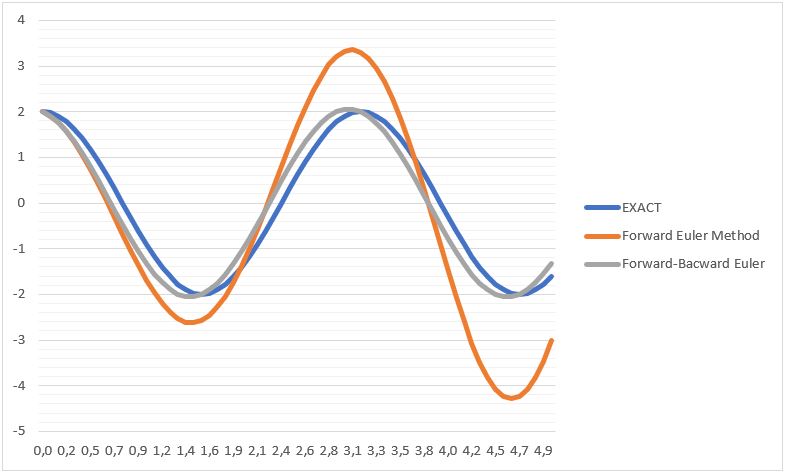Disatu sisi, hasil perhitungan dari metode Backward-Forward Euler menghasilkan hasil yang dekat dengan solusi exact. Hal tersebut dikarenakan prinsip dari metode tersebut yang mana nilai kecepatan osislasi yang dihitung pada node waktu tertentu menggunakan acuan nilai dari posisi pada node sebelumnya, Dengan kata lain, menurut analisis saya, hasi perhitungan tidak akan mengelamai pertumbuhan nilai amplitudo, atau dengan kat alain, nilai amplitudo akan cenderung konstan. Oleh karena itu, pada kasus ini, metode Forward Euler tidak dapat diaplikan pada gerak osilasi sepeti pada kasus yang sedang dibahas. Namun demikian, ada alternatif yang dapat digunakan, diantarnya yaitu dengan memperkecil rentang nilai interval waktu atau nilai ∆t. Misalkan, dengan memperkecil nilai ∆t menjadi 0,1, maka diperoleh hasil: