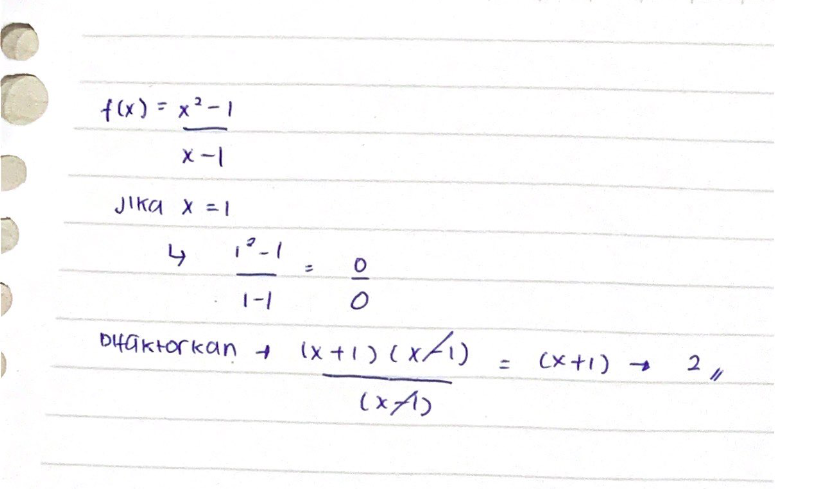Muhammad Raihan Haidar
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Data Diri
Nama : Muhammad Raihan Haidar
NPM : 1606886204
Mahasiswa Departemen Teknik Mesin 2016 Jurusan Teknik Perkapalan
Contents
Pertemuan Pertama Metode Numerik
Hari, Tanggal : Jumat, 7 Februari 2020
Oleh : Dr. Ahmad Indra & Prof. Dr. Ir. Harinaldi M.Eng.
Pada Pertemuan Pertama ini saya di perkenalkan dengan air.eng.ui.ac.id untuk berdiskusi dan mengumpulkan tugas yang diberikan. Alhamdulillah dengan belajar pemrograman nanti nya insyaallah saya dapat mengolah data dengan lebih baik.
Tugas Pengalaman Coding
Perkenalkan nama Saya Muhammad Raihan Haidar, Saya biasa dipanggil Ihan. Saya lahir di Bekasi tanggal 14 Maret 1998.
Pengalaman Saya dengan Pemrograman terutama Coding itu saat saya Praktikum, ketika mengolah data menggunakan excel dan membuat grafik dari data-data tersebut. Selain itu saya juga banyak menggunakan coding di Mata Kuliah Tugas Merancang Kapal (TMK) saat semester 4, 5 dan 6. Pada mata kuliah TMK sangat diperlukan kemampuan coding dan pemrograman karena sangat banyak pengolahan data dan pembuatan grafik.
Tugas Pertama Metode Numerik
Soal T(x)= (x^2-1)/(x-1)
Pada proses Pertama, saya mencoba menyelesaikan persamaan dengan cara manual yaitu dengan memfaktorkan persamaan kemudian memasukan x sebesar 1.
Saya memakai Bahasa python dengan menggunakan software bernama spyder. Di dalam metode ini saya mendefinisikan fungsi yang dicari. Selain itu saya juga menginput x, jadi codingan di metode Pertama ini dapat menyesuaikan Nilai x selain 1.
Algoritma yang saya gunakan pada metode pertama adalah
def h(x):
return (x**2-1)/(x-1)
def f(x):
return(x+1)
x =input ('insert x')
z =int(x)
if z==1: print (f(z))
else : print(h(z))
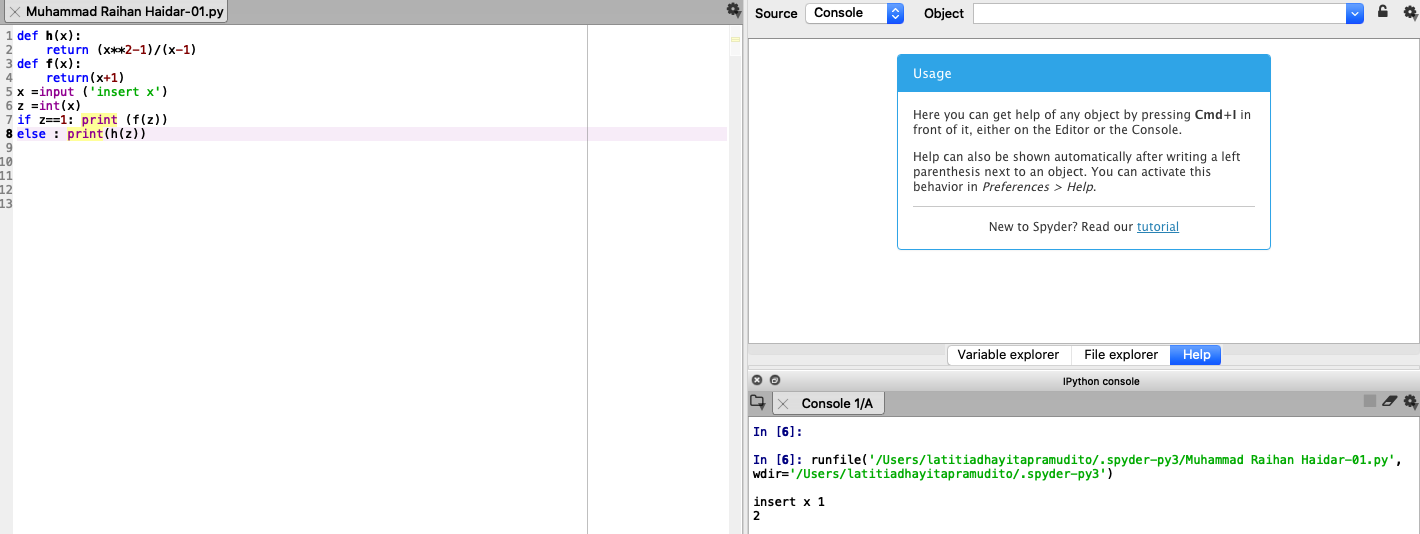
Hasil dari melakukan run pada algoritma diatas adalah :
2
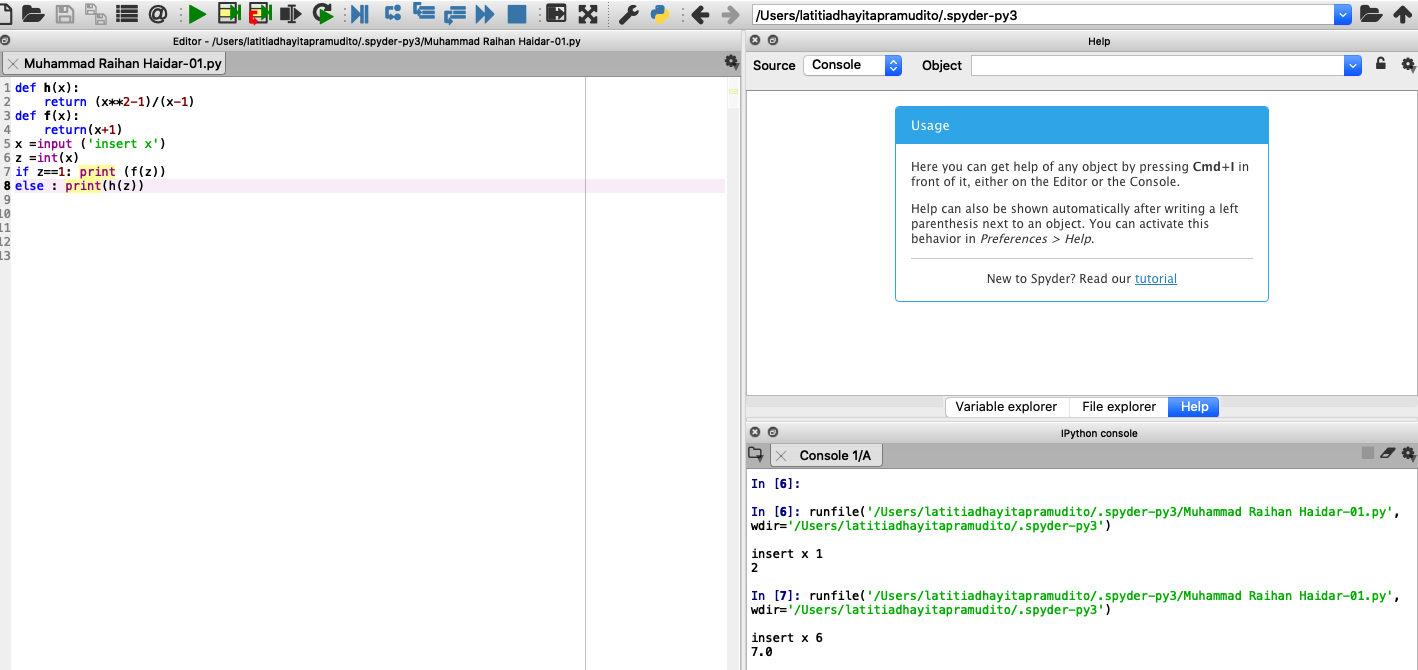
Pada foto dibawah ini saya mencoba menggunakan x sebesar 6, Hasil yang didapatkan adalah sebesar 7
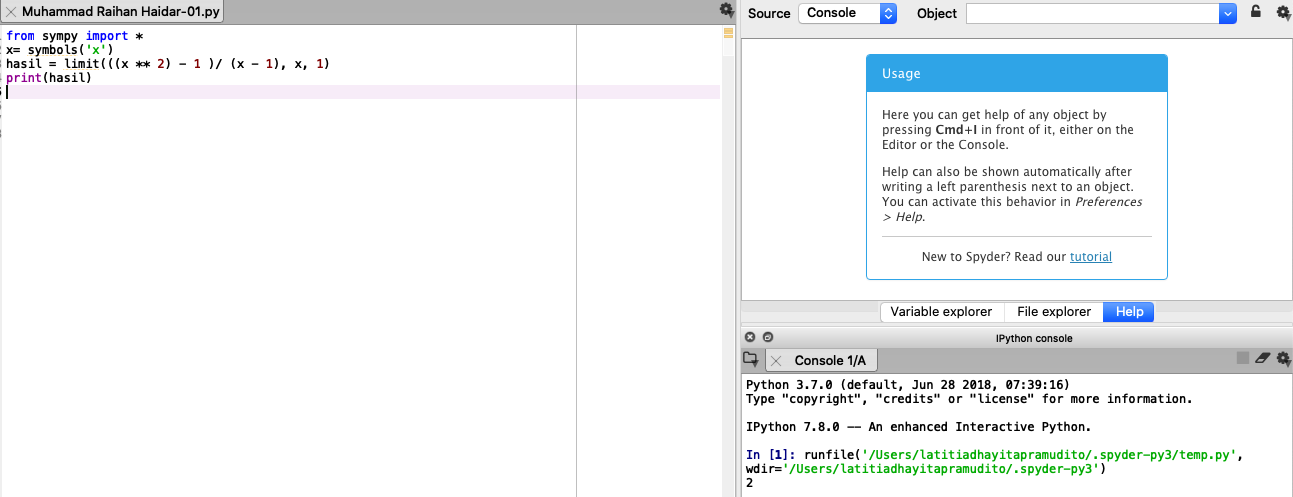
Algoritma yang saya gunakan pada metode dua adalah menggunakan modul sympy
from sympy import *
x= symbols('x')
hasil = limit(((x ** 2) - 1 )/ (x - 1), x, 1)
print(hasil)
Hasil yang didapatkan setelah melakukan run pada algoritma diatas adalah :
2
Dari perhitungan menggunakan 2 metode yaitu manual dan phyton (modul dan definisi) didapatkan bahwa untuk menyelesaikan persamaan lebih mudah menggunakan metode Phyton karena dengan membuat satu codingan dapat memvariasikan nilai variabel x
Pertemuan Kedua Metode Numerik
Hari, Tanggal : Jumat, 14 Februari 2020
Oleh : Dr. Ahmad Indra & Prof. Dr. Ir. Harinaldi M.Eng.
Pada pertemuan kali ini diajarkan untuk menggunakan bahasa phyton untuk menyelesaikan masalah-masalah di matakuliah khususnya dalam hitungan seperti menghitung percepatan pada buah kelapa yang jatuh, ataupun menyelesaikan soal aljabar linear. Hari ini juga kembali mereview materi pertemuan sebelumnya agar mahasiswa tetap selalu ingat materi pada setiap pertemuan. Motivasi agar terus semangat dalam belajar adalah dengan mendorong diri untuk bertanggung jawab pada Allah SWT.
Tugas Kedua Metode Numerik
Bagian A (Aljabar Linear)
Mengambil soal dari buku :
bagian_a_soal.PNG)
Hasil Perhitungan Menggunakan Manual :
bagian_a_soal_manual.PNG)
Hasil Perhitungan Menggunakan Bantuan Bahasa Python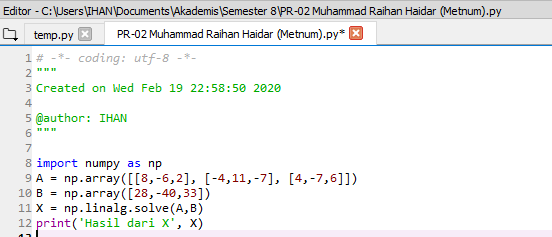
bagian_a.PNG)
Didapatkan hasil sebesar :
Coding yang digunakan :
import numpy as np
A = np.array([[8,-6,2), [-4,11,-7], [4,-7,6]])
B = np.array([28,-40,33])
X = np.linalg.solve(A,B)
print('Hasil dari X', X)
bagian_a_console.PNG)
Dari perhitungan soal matriks aljabar linear diatas didapatkan dengan metode manual dan metode bahasa phyton memiliki hasil yang sama. Namun dalam pengerjaannya jelas lebih mudah menggunakan metode bahasa phyton karena lebih ringkas dan cepat serta juga dapat menghindari kesalahan-kesalahan hitung yang biasa disebut human error.
Bagian B (Initial Value Problem)
Dengan menggunakan soal gerak jatuh bebas pada sebuah buah kelapa
Hasil Perhitungan Manual :
bagian_b_soal_manual.PNG)
Hasil Perhitungan Menggunakan Bantuan Bahasa Python :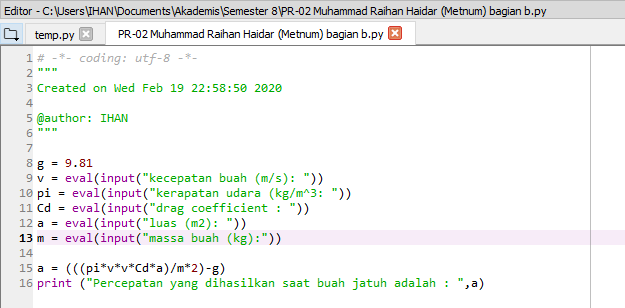
bagian_b_new.PNG)
Didapatkan hasil sebesar :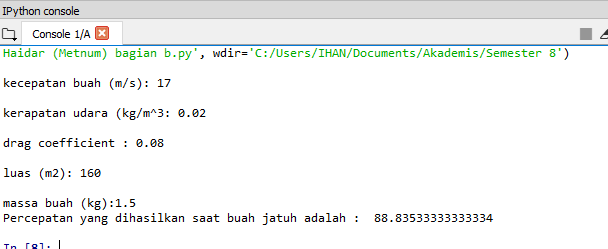
bagian_b_console_new.PNG)
Coding yang digunakan :
g = 9.81
v = eval(input("kecepatan buah (m/s): "))
pi = eval(input("kerapatan udara (kg/m^3: "))
Cd = eval(input("drag coefficient : "))
a = eval(input("luas (m2): "))
m = eval(input("massa buah (kg):"))
a = (((pi*v*v*Cd*a)/m*2)-g)
print ("Percepatan yang dihasilkan saat buah jatuh adalah : ",a)
Saya menggunakan metode eval(input() agar codingan ini dapat digunakan untuk soal lain yang memiliki identifikasi besaran yang berbeda.
Dari perhitungan soal Initial Value Problem dengan metode manual dan metode bahasa phyton diatas didapatkan hasil yang sama. Namun sangat lebih mudah menggunakan metode bahasa phyton karena memperingkas pekerjaan dan terhindar dari human error.
