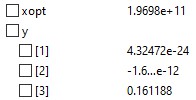Difference between revisions of "Eduardo Christ Soloman"
(→Tugas Besar) |
(→Tugas Besar) |
||
| Line 231: | Line 231: | ||
''''Perhitungan Utama'''' | ''''Perhitungan Utama'''' | ||
model Tugas_Besar_Edo | model Tugas_Besar_Edo | ||
| − | |||
//define initial variable | //define initial variable | ||
parameter Integer Points=size(P,1); //Number of Points | parameter Integer Points=size(P,1); //Number of Points | ||
| Line 238: | Line 237: | ||
parameter Real Area=0.000504; //Area L Profile (Dimension=0.04 x 0.05)(Thickness 0.3) (m2) | parameter Real Area=0.000504; //Area L Profile (Dimension=0.04 x 0.05)(Thickness 0.3) (m2) | ||
parameter Real Elas=195e9; //Elasticity SS 304 (Pa) | parameter Real Elas=195e9; //Elasticity SS 304 (Pa) | ||
| − | |||
//define connection | //define connection | ||
parameter Integer C[:,2]=[1,5; | parameter Integer C[:,2]=[1,5; | ||
| Line 263: | Line 261: | ||
14,15;//3rd floor | 14,15;//3rd floor | ||
15,16;//3rd floor | 15,16;//3rd floor | ||
| − | 13,16];//3rd floor | + | 13,16];//3rd floor |
| − | |||
//define coordinates (please put orderly) | //define coordinates (please put orderly) | ||
parameter Real P[:,6]=[-0.3,0.375,0,1,1,1; //1 | parameter Real P[:,6]=[-0.3,0.375,0,1,1,1; //1 | ||
| Line 284: | Line 281: | ||
0.3,0.375,1.8,0,0,0; //14 | 0.3,0.375,1.8,0,0,0; //14 | ||
0.3,-0.375,1.8,0,0,0; //15 | 0.3,-0.375,1.8,0,0,0; //15 | ||
| − | -0.3,-0.375,1.8,0,0,0]; //16 | + | -0.3,-0.375,1.8,0,0,0]; //16 |
| − | |||
//define external force (please put orderly) | //define external force (please put orderly) | ||
parameter Real F[Points*3]={0,0,0, | parameter Real F[Points*3]={0,0,0, | ||
| Line 303: | Line 299: | ||
0,0,-500, | 0,0,-500, | ||
0,0,-1000}; | 0,0,-1000}; | ||
| − | |||
//solution | //solution | ||
Real displacement[N], reaction[N]; | Real displacement[N], reaction[N]; | ||
Real check[3]; | Real check[3]; | ||
| − | |||
Real stress1[Trusses]; | Real stress1[Trusses]; | ||
Real safety[Trusses]; | Real safety[Trusses]; | ||
Real dis[3]; | Real dis[3]; | ||
Real Str[3]; | Real Str[3]; | ||
| − | |||
protected | protected | ||
parameter Integer N=3*Points; | parameter Integer N=3*Points; | ||
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
Real err=10e-10, ers=10e-4; | Real err=10e-10, ers=10e-4; | ||
| − | |||
algorithm | algorithm | ||
//Creating Global Matrix | //Creating Global Matrix | ||
| Line 325: | Line 317: | ||
q1[j]:=P[C[i,1],j]; | q1[j]:=P[C[i,1],j]; | ||
q2[j]:=P[C[i,2],j]; | q2[j]:=P[C[i,2],j]; | ||
| − | end for; | + | end for; |
| − | |||
//Solving Matrix | //Solving Matrix | ||
L:=Modelica.Math.Vectors.length(q2-q1); | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| Line 335: | Line 326: | ||
cy*cx,cy^2,cy*cz; | cy*cx,cy^2,cy*cz; | ||
cz*cx,cz*cy,cz^2]; | cz*cx,cz*cy,cz^2]; | ||
| − | |||
//Transforming to global matrix | //Transforming to global matrix | ||
g:=zeros(N,N); | g:=zeros(N,N); | ||
| Line 344: | Line 334: | ||
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
end for; | end for; | ||
| − | |||
G_star:=G+g; | G_star:=G+g; | ||
G:=G_star; | G:=G_star; | ||
end for; | end for; | ||
| − | |||
//Implementing boundary | //Implementing boundary | ||
for x in 1:Points loop | for x in 1:Points loop | ||
| Line 370: | Line 358: | ||
end if; | end if; | ||
end for; | end for; | ||
| − | |||
//Solving displacement | //Solving displacement | ||
displacement:=Modelica.Math.Matrices.solve(G,F); | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| − | |||
//Solving reaction | //Solving reaction | ||
reaction:=(G_star*displacement)-F; | reaction:=(G_star*displacement)-F; | ||
| − | |||
//Eliminating float error | //Eliminating float error | ||
for i in 1:N loop | for i in 1:N loop | ||
| Line 382: | Line 367: | ||
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
end for; | end for; | ||
| − | |||
//Checking Force | //Checking Force | ||
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| − | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); |
| − | |||
for i in 1:3 loop | for i in 1:3 loop | ||
check[i] := if abs(check[i])<=ers then 0 else check[i]; | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
end for; | end for; | ||
| − | |||
//Calculating stress in each truss | //Calculating stress in each truss | ||
for i in 1:Trusses loop | for i in 1:Trusses loop | ||
| Line 398: | Line 380: | ||
q2[j]:=P[C[i,2],j]; | q2[j]:=P[C[i,2],j]; | ||
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| − | end for; | + | end for; |
| − | |||
//Solving Matrix | //Solving Matrix | ||
L:=Modelica.Math.Vectors.length(q2-q1); | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| Line 407: | Line 388: | ||
X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
cy*cx,cy^2,cy*cz; | cy*cx,cy^2,cy*cz; | ||
| − | cz*cx,cz*cy,cz^2]; | + | cz*cx,cz*cy,cz^2]; |
| − | |||
Str:=(X*dis); | Str:=(X*dis); | ||
stress1[i]:=Modelica.Math.Vectors.length(Str); | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
end for; | end for; | ||
| − | |||
//Safety factor | //Safety factor | ||
for i in 1:Trusses loop | for i in 1:Trusses loop | ||
| Line 421: | Line 400: | ||
end if; | end if; | ||
end for; | end for; | ||
| − | |||
end Tugas_Besar_Edo; | end Tugas_Besar_Edo; | ||
| Line 464: | Line 442: | ||
Kemudian ditentukan 3 variasi material dengan Yield Strength untuk melihat perbandingan (Safety Factor/Harga) untuk mendapatkan rasio: | Kemudian ditentukan 3 variasi material dengan Yield Strength untuk melihat perbandingan (Safety Factor/Harga) untuk mendapatkan rasio: | ||
| − | [[File:Edodo16.jpg| | + | [[File:Edodo16.jpg|500px|center]] |
Data Yield Strength dan Rasio kemudian digunakan untuk dioptimasikan dan dicari apa material yang optimum untuk trusses dengan luas 0.000171 m^2 dan didapatkan: | Data Yield Strength dan Rasio kemudian digunakan untuk dioptimasikan dan dicari apa material yang optimum untuk trusses dengan luas 0.000171 m^2 dan didapatkan: | ||
| − | [[File:edodo17.jpg| | + | [[File:edodo17.jpg|300px|center]] |
Berdasarkan Hasil Perhitungan, maka dapat disimpulkan untuk batang ukuran 30 mm x 30 mm dengan ketebalan 3 mm, dengan luas 0.000171 m, elastisitas materialnya yang paling opmtimum adalah 196.98 GPa dan ukuran material yang paling mendekati yakni SS 201 dengan Elastisitas bahan 197 GPa. | Berdasarkan Hasil Perhitungan, maka dapat disimpulkan untuk batang ukuran 30 mm x 30 mm dengan ketebalan 3 mm, dengan luas 0.000171 m, elastisitas materialnya yang paling opmtimum adalah 196.98 GPa dan ukuran material yang paling mendekati yakni SS 201 dengan Elastisitas bahan 197 GPa. | ||
---- | ---- | ||
| Line 473: | Line 451: | ||
Optimasi Golden Ratio | Optimasi Golden Ratio | ||
model Opt_Gold | model Opt_Gold | ||
| − | |||
parameter Real xd[:]={1.97E+11,1.95E+11,1.93E+11}; | parameter Real xd[:]={1.97E+11,1.95E+11,1.93E+11}; | ||
parameter Real yd[size(xd,1)]={9.37265E-05,4.25557E-05,2.59827E-05}; | parameter Real yd[size(xd,1)]={9.37265E-05,4.25557E-05,2.59827E-05}; | ||
| Line 480: | Line 457: | ||
parameter Integer N=10; // maximum iteration | parameter Integer N=10; // maximum iteration | ||
parameter Real es=0.0001; // maximum error | parameter Real es=0.0001; // maximum error | ||
| − | |||
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
Real xopt, fx; | Real xopt, fx; | ||
protected | protected | ||
Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| − | |||
algorithm | algorithm | ||
xl := xlo; | xl := xlo; | ||
xu := xhi; | xu := xhi; | ||
y := Curve_Fitting(xd,yd); | y := Curve_Fitting(xd,yd); | ||
| − | |||
for i in 1:N loop | for i in 1:N loop | ||
d:= R*(xu-xl); | d:= R*(xu-xl); | ||
| Line 497: | Line 471: | ||
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| − | xint:=xu-xl; | + | xint:=xu-xl; |
| − | |||
if f1[i]>f2[i] then | if f1[i]>f2[i] then | ||
xl:=x2[i]; | xl:=x2[i]; | ||
| Line 507: | Line 480: | ||
xopt:=x2[i]; | xopt:=x2[i]; | ||
fx:=f2[i]; | fx:=f2[i]; | ||
| − | end if; | + | end if; |
| − | |||
ea[i]:=(1-R)*abs((xint)/xopt); | ea[i]:=(1-R)*abs((xint)/xopt); | ||
if ea[i]<es then | if ea[i]<es then | ||
| Line 514: | Line 486: | ||
end if; | end if; | ||
end for; | end for; | ||
| − | |||
end Opt_Gold; | end Opt_Gold; | ||
Curve Fitting | Curve Fitting | ||
function Curve_Fitting | function Curve_Fitting | ||
| − | |||
input Real X[:]; | input Real X[:]; | ||
input Real Y[size(X,1)]; | input Real Y[size(X,1)]; | ||
input Integer order=2; | input Integer order=2; | ||
output Real Coe[order+1]; | output Real Coe[order+1]; | ||
| − | |||
protected | protected | ||
Real Z[size(X,1),order+1]; | Real Z[size(X,1),order+1]; | ||
| Line 530: | Line 499: | ||
Real A[order+1,order+1]; | Real A[order+1,order+1]; | ||
Real B[order+1]; | Real B[order+1]; | ||
| − | |||
algorithm | algorithm | ||
| − | |||
for i in 1:size(X,1) loop | for i in 1:size(X,1) loop | ||
for j in 1:(order+1) loop | for j in 1:(order+1) loop | ||
| Line 539: | Line 506: | ||
end for; | end for; | ||
ZTr:=transpose(Z); | ZTr:=transpose(Z); | ||
| − | |||
A:=ZTr*Z; | A:=ZTr*Z; | ||
B:=ZTr*Y; | B:=ZTr*Y; | ||
Coe:=Modelica.Math.Matrices.solve(A,B); | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| − | |||
end Curve_Fitting; | end Curve_Fitting; | ||
Revision as of 10:05, 13 January 2021
Biodata Diri
Nama : Eduardo Christ Soloman
NPM : 1806201182
TTL : Jakarta, 29 Februari 2000
Hobi : Bersepeda, Baca Komik
Saya adalah mahasiswa FTUI angkatan 2018 dari jurusan Teknik Mesin.
Saya merupakan mahasiswa jurusan teknik mesin. Saya selalu termotivasi untuk mengembangkan kemampuan saya baik akademik maupun non akademik, dengan cara belajar baik di dalam maupun diluar universitas.
Contents
Mata Kuliah Metode Numerik
Selama pelajaran metode numerika sebelum uts ini, saya belajar tentang konsep dasar dari metode numerik, dan tentang metode-metode yang dapat kami gunakan dalam perhitungan metode numerik. selain itu, saya juga belajar mengenai pengaplikasian dari metode numerik dalam menyelesaikan problema yang sesungguhnya. terakhir, kami juga belajar mengenai coding yang dipakai pada aplikasi matlab untuk melakukan perhitungan menggunakan metode numerik.
Pertemuan 1 (11 Nov 2020)
Pada pertemuan pertama ini, dipaparkan tujuan belajar Metode Numerik, yakni: 1. Memahami konsep dan prinsip dasar dalam metode numerik. contohnya adalah persamaan aljabar, agoritma, pencocokan kurva, persamaan diferensia, parsial, dan lain lain. 2. Mengerti aplikasi metode numerik. 3. Mampu Menerapkan metode numerik dalam persoalan teknik. 4. Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab.
Tugas 1
Berikut adalah hasil dari tugas 1 dimana saya diminta untuk membuat video tentang pembelajaran saya mengenai aplikasi openmodelica.
Pertemuan 2 (18 Nov 2020)
Pada pertemuan kedua ini, kami diminta untuk menunjukan apa saja yang sudah kami pelajari tentang Open Modelica. Selain itu, kami juga diajari mengenai hal baru di dalam aplikasi Open Modelica, yakni mengenai kelas panggil serta kelas fungsi. Dalam kelas function, kami bisa membuat input serta output, dan juga membuat algoritma, kemudian dengan menggunakan kelas panggil, kami dapat memanggil input serta output dari kelas function tadi untuk menyelesaikan suatu problema matematika seperti yang kami kerjakan dalam Tugas 2.
Tugas 2
Berikut adalah hasil dari tugas 2 dimana saya diminta untuk membuat video tentang kelas fungsi dalam aplikasi OpenModelica.
Pertemuan 3 (25 Nov 2020)
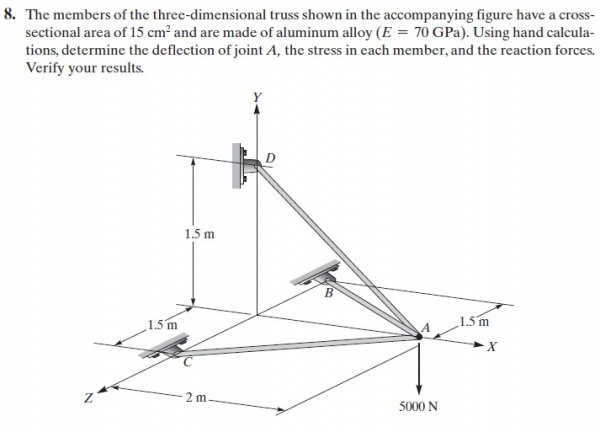
Pada pertemuan ketiga ini, kami diminta untuk menunjukan hasil mengerjakan tugas 2 kami kemarin, selain itu kami juga diberi tugas untuk mengimplementasikan psuedocode pada Figure 9.4 di modelica yang mana nantinya akan di test coding dengan example 9.5.
Tugas 3
model No4
parameter Real A= 0.001; //Area parameter Real E= 2*10^11; //Modulus Young parameter Real L1= 1; //Panjang A parameter Real L2= 1; //Panjang B parameter Real L3= 1.6; //Panajang C parameter Real L4= 1.25; //Panjang D parameter Real L5= 1.6; //Panjang E parameter Real T1= 0; parameter Real T2= 0; parameter Real T3= -0.67; parameter Real T4= -1.57; parameter Real T5= -2.25;
Real k1; Real k2; Real k3; Real k4; Real k5; Real K1 [8,8]; Real K2 [8,8]; Real K3 [8,8]; Real K4 [8,8]; Real K5 [8,8];
Real a1 [8,8] = [(cos(T1))^2,sin(T1)*cos(T1),-(cos(T1))^2,-(sin(T1)*cos(T1)),0,0,0,0;
sin(T1)*cos(T1),(sin(T1))^2,-(sin(T1)*cos(T1)),-(sin(T1))^2,0,0,0,0;
-(cos(T1))^2,-(sin(T1)*cos(T1)),(cos(T1))^2,sin(T1)*cos(T1),0,0,0,0;
-(sin(T1)*cos(T1)),-(sin(T1))^2,sin(T1)*cos(T1),(sin(T1))^2,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0];
Real a2 [8,8] = [0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,(cos(T2))^2,sin(T2)*cos(T2),-(cos(T2))^2,-(sin(T2)*cos(T2)),0,0;
0,0,sin(T2)*cos(T2),(sin(T2))^2,-(sin(T2)*cos(T2)),-(sin(T2))^2,0,0;
0,0,-(cos(T2))^2,-(sin(T2)*cos(T2)),(cos(T2))^2,sin(T2)*cos(T2),0,0;
0,0,-(sin(T2)*cos(T2)),-(sin(T2))^2,sin(T2)*cos(T2),(sin(T2))^2,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0];
Real a3 [8,8] = [(cos(T3))^2,sin(T3)*cos(T3),0,0,0,0,-(cos(T3))^2,-(sin(T3)*cos(T3));
sin(T3)*cos(T3),(sin(T3))^2,0,0,0,0,-(sin(T3)*cos(T3)),-(sin(T3))^2;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
-(cos(T3))^2,-(sin(T3)*cos(T3)),0,0,0,0,(cos(T3))^2,sin(T3)*cos(T3);
-(sin(T3)*cos(T3)),-(sin(T3))^2,0,0,0,0,sin(T3)*cos(T3),(sin(T3))^2];
Real a4 [8,8] = [0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,(cos(T4))^2,sin(T4)*cos(T4),0,0,-(cos(T4))^2,-(sin(T4)*cos(T4));
0,0,sin(T4)*cos(T4),(sin(T4))^2,0,0,-(sin(T4)*cos(T4)),-(sin(T4))^2;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,-(cos(T4))^2,-(sin(T4)*cos(T4)),0,0,(cos(T4))^2,sin(T4)*cos(T4);
0,0,-(sin(T4)*cos(T4)),-(sin(T4))^2,0,0,sin(T4)*cos(T4),(sin(T4))^2];
Real a5 [8,8] = [0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,(cos(T5))^2,sin(T5)*cos(T5),-(cos(T5))^2,-(sin(T5)*cos(T5));
0,0,0,0,sin(T5)*cos(T5),(sin(T5))^2,-(sin(T5)*cos(T5)),-(sin(T5))^2;
0,0,0,0,-(cos(T5))^2,-(sin(T5)*cos(T5)),(cos(T5))^2,sin(T5)*cos(T5);
0,0,0,0,-(sin(T5)*cos(T5)),-(sin(T5))^2,sin(T5)*cos(T1),(sin(T5))^2];
equation k1= A*E/L1; k2= A*E/L2; k3= A*E/L3; k4= A*E/L4; k5= A*E/L5; K1= k1*a1; K2= k2*a2; K3= k3*a3; K4= k4*a4; K5= k5*a5;
end No4;
Kuis Flowchart dan Diagram Class
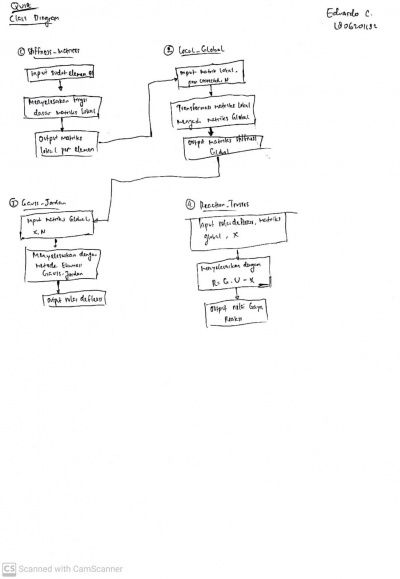
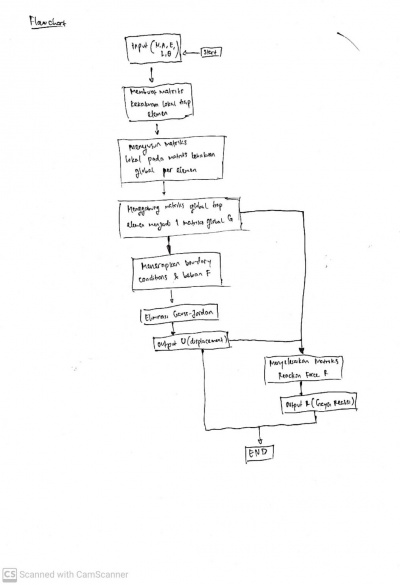
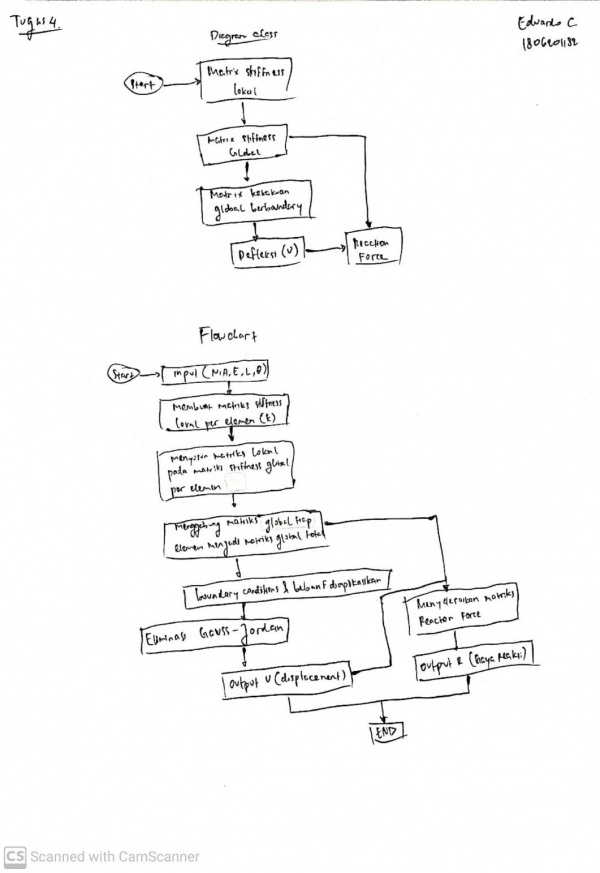
Berdasarkan yang saya dapat dari penjelasan josiah mengenai jawabannya untuk tugas 3, saya membuat Class Diagram dan Flowchart berikut
Tugas 4
Diagram Class dan Flow Chart
Pertemuan 4 (16 Desember 2020)
Aplikasi Metode Numerik Dalam Kasus Optimasi
Fungsi yang ingin diselesaikan
function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:= 2*sin(x)-x^2/10; end f_obj3;
Golden Section Optimization
model Bracket parameter Integer n=8; Real x1 [n]; Real x2 [n]; Real xup; Real xlow; Real d; Real f1 [n]; Real f2 [n]; Real xopt; Real yopt;
equation xup :=4; xlow:=0;
for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= f_obj3(x1[i]); f2[i]:= f_obj3(x2[i]); if f1[i]>f2[i] then xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; end Bracket;
Tugas Besar
Pendahuluan
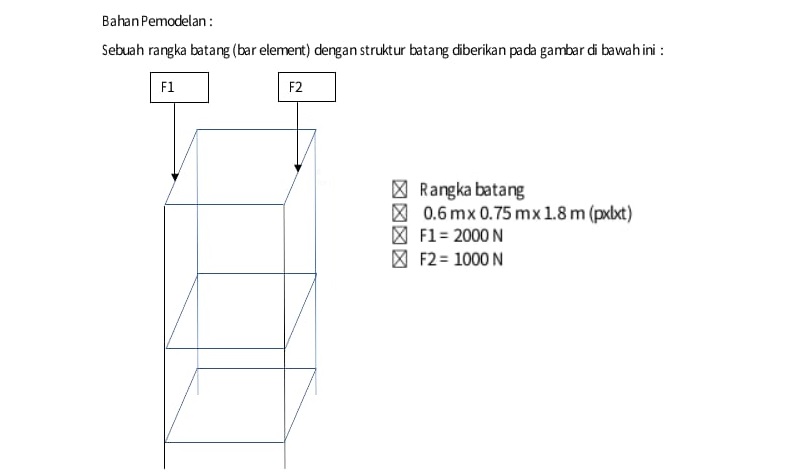
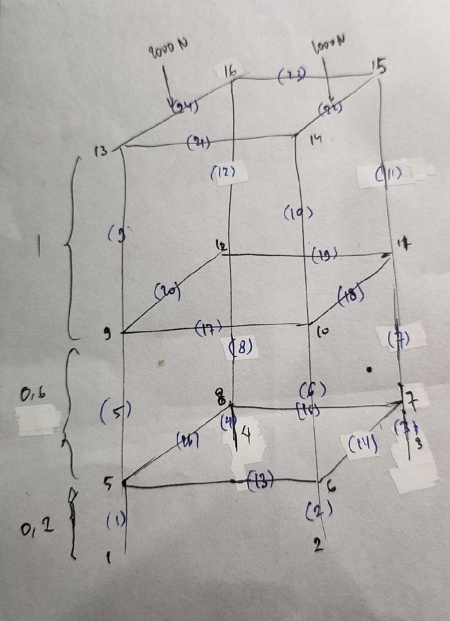
Pada tugas besar ini, kami diberikan sebuah tugas untuk melakukan optimisasi pemilihan material dan luas penampang trusses yang akan digunakan untuk membuat konstruksi sebagai berikut:
Asumsi yang Digunakan dalam Tugas Besar
Sumber: http://asm.matweb.com/search/SpecificMaterial.asp?bassnum=MQ304A
Variabel bebas/faktor lainnya yang perlu ditentukan adalah jenis material (elastisitas), harga material, dan luas cross section Truss (dengan L profile). Kami diminta untuk mencari optimasi dan membentuk kurva efisiensi harga dengan Curve Fitting, serta menentukan nilai optimum dengan cost terendah.
1. Beban terdistribusi pada node
2. Titik perpotongan antara node 1, node 2, node 3, dan node 4 terletak pada titik pusat koordinat (0,0,0)
3. Jenis material yang digunakan : Stainless Steel AISI 304
'Coding'
'Perhitungan Utama'
model Tugas_Besar_Edo
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000504; //Area L Profile (Dimension=0.04 x 0.05)(Thickness 0.3) (m2)
parameter Real Elas=195e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[-0.3,0.375,0,1,1,1; //1
0.3,0.375,0,1,1,1; //2
0.3,-0.375,0,1,1,1; //3
-0.3,-0.375,0,1,1,1; //4
-0.3,0.375,0.2,0,0,0; //5
0.3,0.375,0.2,0,0,0; //6
0.3,-0.375,0.2,0,0,0; //7
-0.3,-0.375,0.2,0,0,0; //8
-0.3,0.375,0.8,0,0,0; //9
0.3,0.375,0.8,0,0,0; //10
0.3,-0.375,0.8,0,0,0; //11
-0.3,-0.375,0.8,0,0,0; //12
-0.3,0.375,1.8,0,0,0; //13
0.3,0.375,1.8,0,0,0; //14
0.3,-0.375,1.8,0,0,0; //15
-0.3,-0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Tugas_Besar_Edo;
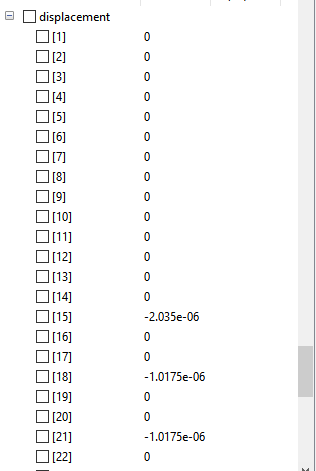
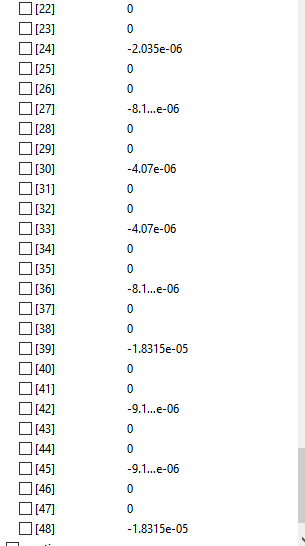
'Hasil Perhitungan Menggunakan OpenModelica'
Displacement
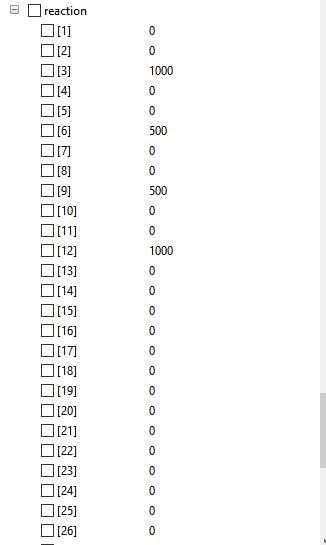
Reaction
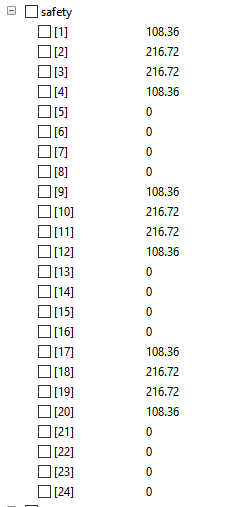
Safety Factor
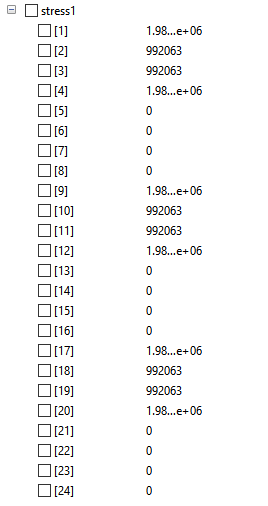
Stress pada Tiap Truss
'Analisis Optimasi'
Metode Analisis Optimasi Material Sama
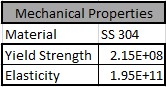
Pada metode ini, material yang digunakan adalah stainless steel 304 sebagai material referensi yang memiliki mechanical properties:
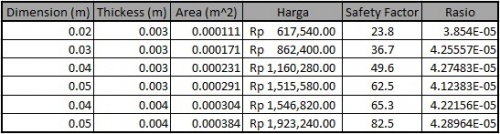
Kemudian ditentukan 6 variasi luas untuk melihat perbandingan (Safety Factor/Harga) untuk mendapatkan rasio:
Data Luas dan Rasio kemudian digunakan untuk dioptimasikan dan dicari berapa luas optimum untuk material SS 304 dan didapatkan:
Berdasarkan Hasil Perhitungan, maka dapat disimpulkan untuk material SS 304, Luas opmtimalnya adalah 0.00031237 m^2 dan ukuran truss yang paling mendekati yakni batang ukuran 40 mm x 40 mm dengan ketebalan 4 mm
Metode Analisis Optimasi Luas Sama
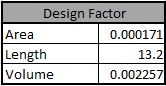
Pada metode ini, Luas yang digunakan sebagai referensi adalah:
Kemudian ditentukan 3 variasi material dengan Yield Strength untuk melihat perbandingan (Safety Factor/Harga) untuk mendapatkan rasio:
Data Yield Strength dan Rasio kemudian digunakan untuk dioptimasikan dan dicari apa material yang optimum untuk trusses dengan luas 0.000171 m^2 dan didapatkan:
Berdasarkan Hasil Perhitungan, maka dapat disimpulkan untuk batang ukuran 30 mm x 30 mm dengan ketebalan 3 mm, dengan luas 0.000171 m, elastisitas materialnya yang paling opmtimum adalah 196.98 GPa dan ukuran material yang paling mendekati yakni SS 201 dengan Elastisitas bahan 197 GPa.
Coding Optimasi Golden Ratio
model Opt_Gold
parameter Real xd[:]={1.97E+11,1.95E+11,1.93E+11};
parameter Real yd[size(xd,1)]={9.37265E-05,4.25557E-05,2.59827E-05};
parameter Real xlo=0.000111;
parameter Real xhi=0.000384;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Curve Fitting
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;