Difference between revisions of "Tedi Veradino"

From ccitonlinewiki
Jump to: navigation, search
Line 123: Line 123:
  
 
model Trusses
 
model Trusses
 +
 +
parameter Integer N=10; //Global matrice = 2*points connected
 +
parameter Real A=8;
 +
parameter Real E=1.9e6;
 +
Real G[N,N]; //global
 +
Real Ginitial[N,N]; //global
 +
Real Sol[N]; //global dispplacement
 +
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
 +
Real R[N]; //global reaction force
 +
Real SolMat[N,1];
 +
Real XMat[N,1];
 +
 +
//boundary coundition
 +
Integer b1=1;
 +
Integer b2=3;
 +
 +
//truss 1
 +
parameter Real X1=0; //degree between truss
 +
Real k1=A*E/36;
 +
Real K1[4,4]; //stiffness matrice
 +
Integer p1a=1;
 +
Integer p1b=2;
 +
Real G1[N,N];
 +
 +
//truss 2
 +
parameter Real X2=135; //degree between truss
 +
Real k2=A*E/50.912;
 +
Real K2[4,4]; //stiffness matrice
 +
Integer p2a=2;
 +
Integer p2b=3;
 +
Real G2[N,N];
 +
 +
//truss 3
 +
parameter Real X3=0; //degree between truss
 +
Real k3=A*E/36;
 +
Real K3[4,4]; //stiffness matrice
 +
Integer p3a=3;
 +
Integer p3b=4;
 +
Real G3[N,N];
 +
 +
//truss 4
 +
parameter Real X4=90; //degree between truss
 +
Real k4=A*E/36;
 +
Real K4[4,4]; //stiffness matrice
 +
Integer p4a=2;
 +
Integer p4b=4;
 +
Real G4[N,N];
 +
 +
//truss 5
 +
parameter Real X5=45; //degree between truss
 +
Real k5=A*E/50.912;
 +
Real K5[4,4]; //stiffness matrice
 +
Integer p5a=2;
 +
Integer p5b=5;
 +
Real G5[N,N];
 +
 +
//truss 6
 +
parameter Real X6=0; //degree between truss
 +
Real k6=A*E/36;
 +
Real K6[4,4]; //stiffness matrice
 +
Integer p6a=4;
 +
Integer p6b=5;
 +
Real G6[N,N];
 +
 +
/*
 +
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
 +
*/
 +
 +
algorithm
 +
 +
//creating global matrice
 +
K1:=Stiffness_Matrices(X1);
 +
G1:=k1*Local_Global(K1,N,p1a,p1b);
 +
 +
K2:=Stiffness_Matrices(X2);
 +
G2:=k2*Local_Global(K2,N,p2a,p2b);
 +
 +
K3:=Stiffness_Matrices(X3);
 +
G3:=k3*Local_Global(K3,N,p3a,p3b);
 +
 +
K4:=Stiffness_Matrices(X4);
 +
G4:=k4*Local_Global(K4,N,p4a,p4b);
 +
 +
K5:=Stiffness_Matrices(X5);
 +
G5:=k5*Local_Global(K5,N,p5a,p5b);
 +
 +
K6:=Stiffness_Matrices(X6);
 +
G6:=k6*Local_Global(K6,N,p6a,p6b);
 +
 +
G:=G1+G2+G3+G4+G5+G6;
 +
Ginitial:=G;
 +
 +
//implementing boundary condition
 +
for i in 1:N loop
 +
  G[2*b1-1,i]:=0;
 +
  G[2*b1,i]:=0;
 +
  G[2*b2-1,i]:=0;
 +
  G[2*b2,i]:=0;
 +
end for;
 +
 +
G[2*b1-1,2*b1-1]:=1;
 +
G[2*b1,2*b1]:=1;
 +
G[2*b2-1,2*b2-1]:=1;
 +
G[2*b2,2*b2]:=1;
 +
 +
//solving displacement
 +
Sol:=Gauss_Jordan(N,G,X);
 +
 +
//solving reaction force
 +
SolMat:=matrix(Sol);
 +
XMat:=matrix(X);
 +
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
 +
 +
end Trusses;
 +
|}
  
−
parameter Integer N=10; //Global matrice = 2*points connected
 
−
parameter Real A=8;
 
−
parameter Real E=1.9e6;
 
−
Real G[N,N]; //global
 
−
Real Ginitial[N,N]; //global
 
−
Real Sol[N]; //global dispplacement
 
−
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
 
−
Real R[N]; //global reaction force
 
−
Real SolMat[N,1];
 
−
Real XMat[N,1];
 
  
−
//boundary coundition
+
==== Trusses Problem 2 (Homework) ====
−
Integer b1=1;
+
[[File:Soal_Trusses_2_fashal.jpg|450px|thumb|center]]
−
Integer b2=3;
 
  
−
//truss 1
 
−
parameter Real X1=0; //degree between truss
 
−
Real k1=A*E/36;
 
−
Real K1[4,4]; //stiffness matrice
 
−
Integer p1a=1;
 
−
Integer p1b=2;
 
−
Real G1[N,N];
 
  
−
//truss 2
+
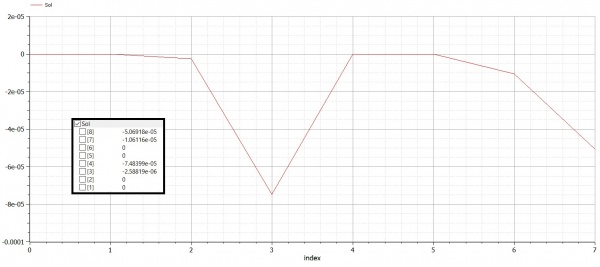
[[File:600px-Soal_Trusses_2_Displacement_fashal.jpg|600px|thumb|right|Discplacement Graphics]]
−
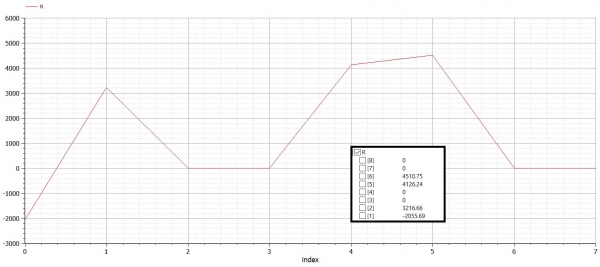
parameter Real X2=135; //degree between truss
+
[[File:600px-Soal Trusses 2 Reaction fashal.jpg|600px|thumb|right| Reaction Forces Graphics]]
−
Real k2=A*E/50.912;
+
{| class="wikitable"
−
Real K2[4,4]; //stiffness matrice
+
|-
−
Integer p2a=2;
+
| style='border-style: none  none  solid  solid;' |
−
Integer p2b=3;
+
''Persamaan''
−
Real G2[N,N];
 
  
−
//truss 3
+
class Trusses_HW
−
parameter Real X3=0; //degree between truss
+
−
Real k3=A*E/36;
+
parameter Integer N=8; //Global matrice = 2*points connected
−
Real K3[4,4]; //stiffness matrice
+
parameter Real A=0.001; //Area m2
−
Integer p3a=3;
+
parameter Real E=200e9; //Pa
−
Integer p3b=4;
+
Real G[N,N]; //global
−
Real G3[N,N];
+
Real Ginitial[N,N]; //global
 +
Real Sol[N]; //global dispplacement
 +
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
 +
Real R[N]; //global reaction force
 +
Real SolMat[N,1];
 +
Real XMat[N,1];
 +
 +
//boundary condition
 +
Integer b1=1;
 +
Integer b2=3;
 +
 +
//truss 1
 +
parameter Real X1=0; //degree between truss
 +
Real k1=A*E/1;
 +
Real K1[4,4]; //stiffness matrice
 +
Integer p1a=1;
 +
Integer p1b=2;
 +
Real G1[N,N];
 +
 +
//truss 2
 +
parameter Real X2=0; //degree between truss
 +
Real k2=A*E/1;
 +
Real K2[4,4]; //stiffness matrice
 +
Integer p2a=2;
 +
Integer p2b=3;
 +
Real G2[N,N];
 +
 +
//truss 3
 +
parameter Real X3=90; //degree between truss
 +
Real k3=A*E/1.25;
 +
Real K3[4,4]; //stiffness matrice
 +
Integer p3a=2;
 +
Integer p3b=4;
 +
Real G3[N,N];
 +
 +
//truss 4
 +
parameter Real X4=90+38.6598; //degree between truss
 +
Real k4=A*E/1.6;
 +
Real K4[4,4]; //stiffness matrice
 +
Integer p4a=1;
 +
Integer p4b=4;
 +
Real G4[N,N];
 +
 +
//truss 5
 +
parameter Real X5=90-38.6598; //degree between truss
 +
Real k5=A*E/1.6;
 +
Real K5[4,4]; //stiffness matrice
 +
Integer p5a=3;
 +
Integer p5b=4;
 +
Real G5[N,N];
 +
 +
/*
 +
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
 +
*/
 +
 +
algorithm
 +
 +
//creating global matrice
 +
K1:=Stiffness_Matrices(X1);
 +
G1:=k1*Local_Global(K1,N,p1a,p1b);
 +
 +
K2:=Stiffness_Matrices(X2);
 +
G2:=k2*Local_Global(K2,N,p2a,p2b);
 +
 +
K3:=Stiffness_Matrices(X3);
 +
G3:=k3*Local_Global(K3,N,p3a,p3b);
 +
 +
K4:=Stiffness_Matrices(X4);
 +
G4:=k4*Local_Global(K4,N,p4a,p4b);
 +
 +
K5:=Stiffness_Matrices(X5);
 +
G5:=k5*Local_Global(K5,N,p5a,p5b);
 +
 +
G:=G1+G2+G3+G4+G5;
 +
Ginitial:=G;
 +
 +
//implementing boundary condition
 +
for i in 1:N loop
 +
  G[2*b1-1,i]:=0;
 +
  G[2*b1,i]:=0;
 +
  G[2*b2-1,i]:=0;
 +
  G[2*b2,i]:=0;
 +
end for;
 +
 +
G[2*b1-1,2*b1-1]:=1;
 +
G[2*b1,2*b1]:=1;
 +
G[2*b2-1,2*b2-1]:=1;
 +
G[2*b2,2*b2]:=1;
 +
 +
//solving displacement
 +
Sol:=Gauss_Jordan(N,G,X);
 +
 +
//solving reaction force
 +
SolMat:=matrix(Sol);
 +
XMat:=matrix(X);
 +
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
 +
 +
end Trusses_HW;
 +
|}
  
−
//truss 4
+
'''Fungsi Panggil'''
−
parameter Real X4=90; //degree between truss
 
−
Real k4=A*E/36;
 
−
Real K4[4,4]; //stiffness matrice
 
−
Integer p4a=2;
 
−
Integer p4b=4;
 
−
Real G4[N,N];
 
  
−
//truss 5
+
{| class="wikitable"
−
parameter Real X5=45; //degree between truss
+
|-
−
Real k5=A*E/50.912;
+
| style='border-style: none  none  solid  solid;' |
−
Real K5[4,4]; //stiffness matrice
+
''Matrice Transformation''
−
Integer p5a=2;
 
−
Integer p5b=5;
 
−
Real G5[N,N];
 
  
−
//truss 6
+
function Stiffness_Matrices
−
parameter Real X6=0; //degree between truss
+
input Real A;
−
Real k6=A*E/36;
+
Real Y;
−
Real K6[4,4]; //stiffness matrice
+
output Real X[4,4];
−
Integer p6a=4;
+
Real float_error = 10e-10;
−
Integer p6b=5;
+
−
Real G6[N,N];
+
final constant Real pi=2*Modelica.Math.asin(1.0);
 +
 +
algorithm
 +
 +
Y:=A/180*pi;
 +
   
 +
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
 +
 +
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
 +
 +
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
 +
 +
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
 +
 +
for i in 1:4 loop
 +
  for j in 1:4 loop
 +
    if abs(X[i,j]) <= float_error then
 +
      X[i,j] := 0;
 +
    end if;
 +
  end for;
 +
end for;
 +
 +
end Stiffness_Matrices;
 +
 +
| style="width: 20cm;"|
 +
''Global Element Matrice''
  
−
/*
+
function Local_Global
−
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
+
input Real Y[4,4];
−
*/
+
input Integer B;
−
 
+
input Integer p1;
−
algorithm
+
input Integer p2;
−
 
+
output Real G[B,B];
−
//creating global matrice
+
−
K1:=Stiffness_Matrices(X1);
+
algorithm
−
G1:=k1*Local_Global(K1,N,p1a,p1b);
+
−
 
+
for i in 1:B loop
−
K2:=Stiffness_Matrices(X2);
+
  for j in 1:B loop
−
G2:=k2*Local_Global(K2,N,p2a,p2b);
+
      G[i,j]:=0;
−
 
+
  end for;
−
K3:=Stiffness_Matrices(X3);
+
  end for;
−
G3:=k3*Local_Global(K3,N,p3a,p3b);
+
−
 
+
  G[2*p1,2*p1]:=Y[2,2];
−
K4:=Stiffness_Matrices(X4);
+
G[2*p1-1,2*p1-1]:=Y[1,1];
−
G4:=k4*Local_Global(K4,N,p4a,p4b);
+
G[2*p1,2*p1-1]:=Y[2,1];
−
 
+
G[2*p1-1,2*p1]:=Y[1,2];
−
K5:=Stiffness_Matrices(X5);
+
−
G5:=k5*Local_Global(K5,N,p5a,p5b);
+
G[2*p2,2*p2]:=Y[4,4];
−
 
+
G[2*p2-1,2*p2-1]:=Y[3,3];
−
K6:=Stiffness_Matrices(X6);
+
G[2*p2,2*p2-1]:=Y[4,3];
−
G6:=k6*Local_Global(K6,N,p6a,p6b);
+
G[2*p2-1,2*p2]:=Y[3,4];
−
 
+
−
G:=G1+G2+G3+G4+G5+G6;
+
G[2*p2,2*p1]:=Y[4,2];
−
Ginitial:=G;
+
G[2*p2-1,2*p1-1]:=Y[3,1];
−
 
+
G[2*p2,2*p1-1]:=Y[4,1];
−
//implementing boundary condition
+
  G[2*p2-1,2*p1]:=Y[3,2];
−
for i in 1:N loop
+
−
G[2*b1-1,i]:=0;
+
  G[2*p1,2*p2]:=Y[2,4];
−
  G[2*b1,i]:=0;
+
G[2*p1-1,2*p2-1]:=Y[1,3];
−
  G[2*b2-1,i]:=0;
+
G[2*p1,2*p2-1]:=Y[2,3];
−
G[2*b2,i]:=0;
+
G[2*p1-1,2*p2]:=Y[1,4];
−
end for;
+
−
 
+
end Local_Global;
−
G[2*b1-1,2*b1-1]:=1;
+
| style="width: 20cm;"| 
−
G[2*b1,2*b1]:=1;
+
''Gauss_Jordan''
−
G[2*b2-1,2*b2-1]:=1;
 
−
G[2*b2,2*b2]:=1;
 
−
 
 
−
//solving displacement
 
−
Sol:=Gauss_Jordan(N,G,X);
 
−
 
 
−
//solving reaction force
 
−
SolMat:=matrix(Sol);
 
−
XMat:=matrix(X);
 
−
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
 
−
 
 
−
end Trusses;
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
class Trusses_HW
 
−
 
 
−
parameter Integer N=8; //Global matrice = 2*points connected
 
−
parameter Real A=0.001; //Area m2
 
−
parameter Real E=200e9; //Pa
 
−
Real G[N,N]; //global
 
−
Real Ginitial[N,N]; //global
 
−
Real Sol[N]; //global dispplacement
 
−
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
 
−
Real R[N]; //global reaction force
 
−
Real SolMat[N,1];
 
−
Real XMat[N,1];
 
−
 
 
−
//boundary condition
 
−
Integer b1=1;
 
−
Integer b2=3;
 
−
 
 
−
//truss 1
 
−
parameter Real X1=0; //degree between truss
 
−
Real k1=A*E/1;
 
−
Real K1[4,4]; //stiffness matrice
 
−
Integer p1a=1;
 
−
Integer p1b=2;
 
−
Real G1[N,N];
 
−
 
 
−
//truss 2
 
−
parameter Real X2=0; //degree between truss
 
−
Real k2=A*E/1;
 
−
Real K2[4,4]; //stiffness matrice
 
−
Integer p2a=2;
 
−
Integer p2b=3;
 
−
Real G2[N,N];
 
−
 
 
−
//truss 3
 
−
parameter Real X3=90; //degree between truss
 
−
Real k3=A*E/1.25;
 
−
Real K3[4,4]; //stiffness matrice
 
−
Integer p3a=2;
 
−
Integer p3b=4;
 
−
Real G3[N,N];
 
−
 
 
−
//truss 4
 
−
parameter Real X4=90+38.6598; //degree between truss
 
−
Real k4=A*E/1.6;
 
−
Real K4[4,4]; //stiffness matrice
 
−
Integer p4a=1;
 
−
Integer p4b=4;
 
−
Real G4[N,N];
 
−
 
 
−
//truss 5
 
−
parameter Real X5=90-38.6598; //degree between truss
 
−
Real k5=A*E/1.6;
 
−
Real K5[4,4]; //stiffness matrice
 
−
Integer p5a=3;
 
−
Integer p5b=4;
 
−
Real G5[N,N];
 
−
 
 
−
/*
 
−
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
 
−
*/
 
−
 
 
−
algorithm
 
−
 
 
−
//creating global matrice
 
−
K1:=Stiffness_Matrices(X1);
 
−
G1:=k1*Local_Global(K1,N,p1a,p1b);
 
−
 
 
−
K2:=Stiffness_Matrices(X2);
 
−
G2:=k2*Local_Global(K2,N,p2a,p2b);
 
−
 
 
−
K3:=Stiffness_Matrices(X3);
 
−
G3:=k3*Local_Global(K3,N,p3a,p3b);
 
−
 
 
−
K4:=Stiffness_Matrices(X4);
 
−
G4:=k4*Local_Global(K4,N,p4a,p4b);
 
−
 
 
−
K5:=Stiffness_Matrices(X5);
 
−
G5:=k5*Local_Global(K5,N,p5a,p5b);
 
−
 
 
−
G:=G1+G2+G3+G4+G5;
 
−
Ginitial:=G;
 
−
 
 
−
//implementing boundary condition
 
−
for i in 1:N loop
 
−
  G[2*b1-1,i]:=0;
 
−
G[2*b1,i]:=0;
 
−
  G[2*b2-1,i]:=0;
 
−
G[2*b2,i]:=0;
 
−
end for;
 
−
 
 
−
G[2*b1-1,2*b1-1]:=1;
 
−
G[2*b1,2*b1]:=1;
 
−
G[2*b2-1,2*b2-1]:=1;
 
−
G[2*b2,2*b2]:=1;
 
−
 
 
−
//solving displacement
 
−
Sol:=Gauss_Jordan(N,G,X);
 
−
 
 
−
//solving reaction force
 
−
SolMat:=matrix(Sol);
 
−
XMat:=matrix(X);
 
−
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
 
−
 
 
−
end Trusses_HW;
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
function Stiffness_Matrices
 
−
input Real A;
 
−
Real Y;
 
−
output Real X[4,4];
 
−
Real float_error = 10e-10;
 
−
 
 
−
final constant Real pi=2*Modelica.Math.asin(1.0);
 
  
−
algorithm
+
function Gauss_Jordan
 +
input Integer N;
 +
input Real A[N,N];
 +
input Real B[N];
 +
output Real X[N];
 +
Real float_error = 10e-10;
  
−
Y:=A/180*pi;
+
algorithm
−
   
+
X:=Modelica.Math.Matrices.solve(A,B);
−
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
 
  
−
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
+
for i in 1:N loop
−
 
+
   if abs(X[i]) <= float_error then
−
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
+
     X[i] := 0;
−
 
 
−
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
 
−
 
 
−
for i in 1:4 loop
 
−
for j in 1:4 loop
 
−
   if abs(X[i,j]) <= float_error then
 
−
     X[i,j] := 0;
 
 
   end if;
 
   end if;
 
  end for;
 
  end for;
−
end for;
 
−
 
−
end Stiffness_Matrices;
 
−
 
−
 
−
 
−
 
−
 
  
 +
end Gauss_Jordan;
  
 +
| style="width: 20cm;"| 
 +
''Reaction Matrice Equation''
  
−
 
+
function Reaction_Trusses
−
function Gauss_Jordan
+
input Integer N;
−
input Integer N;
+
input Real A[N,N];
−
input Real A[N,N];
+
input Real B[N,1];
−
input Real B[N];
+
input Real C[N,1];
−
output Real X[N];
+
Real X[N,1];
−
Real float_error = 10e-10;
+
output Real Sol[N];
−
 
+
Real float_error = 10e-10;
−
algorithm
+
−
X:=Modelica.Math.Matrices.solve(A,B);
+
algorithm
−
 
+
X:=A*B-C;
−
for i in 1:N loop
+
−
   if abs(X[i]) <= float_error then
+
for i in 1:N loop
−
     X[i] := 0;
+
   if abs(X[i,1]) <= float_error then
 +
     X[i,1] := 0;
 
   end if;
 
   end if;
−
end for;
 
−
 
−
end Gauss_Jordan;
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
function Local_Global
 
−
input Real Y[4,4];
 
−
input Integer B;
 
−
input Integer p1;
 
−
input Integer p2;
 
−
output Real G[B,B];
 
−
 
−
algorithm
 
−
 
−
for i in 1:B loop
 
−
for j in 1:B loop
 
−
    G[i,j]:=0;
 
 
  end for;
 
  end for;
−
end for;
+
−
 
+
for i in 1:N loop
−
G[2*p1,2*p1]:=Y[2,2];
+
  Sol[i]:=X[i,1];
−
G[2*p1-1,2*p1-1]:=Y[1,1];
+
  end for;
−
G[2*p1,2*p1-1]:=Y[2,1];
+
−
G[2*p1-1,2*p1]:=Y[1,2];
+
  end Reaction_Trusses;
−
 
 
−
G[2*p2,2*p2]:=Y[4,4];
 
−
G[2*p2-1,2*p2-1]:=Y[3,3];
 
−
G[2*p2,2*p2-1]:=Y[4,3];
 
−
G[2*p2-1,2*p2]:=Y[3,4];
 
−
 
 
−
G[2*p2,2*p1]:=Y[4,2];
 
−
G[2*p2-1,2*p1-1]:=Y[3,1];
 
−
G[2*p2,2*p1-1]:=Y[4,1];
 
−
G[2*p2-1,2*p1]:=Y[3,2];
 
−
 
 
−
G[2*p1,2*p2]:=Y[2,4];
 
−
G[2*p1-1,2*p2-1]:=Y[1,3];
 
−
G[2*p1,2*p2-1]:=Y[2,3];
 
−
G[2*p1-1,2*p2]:=Y[1,4];
 
−
 
 
−
end Local_Global;
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
function Reaction_Trusses
 
−
input Integer N;
 
−
input Real A[N,N];
 
−
input Real B[N,1];
 
−
input Real C[N,1];
 
−
Real X[N,1];
 
−
output Real Sol[N];
 
−
Real float_error = 10e-10;
 
−
 
 
−
algorithm
 
−
X:=A*B-C;
 
−
 
 
−
for i in 1:N loop
 
−
if abs(X[i,1]) <= float_error then
 
−
  X[i,1] := 0;
 
−
  end if;
 
−
end for;
 
−
 
 
−
for i in 1:N loop
 
−
  Sol[i]:=X[i,1];
 
−
end for;
 
  
−
end Reaction_Trusses;
+
|}

Revision as of 14:17, 2 December 2020

Biodata

Nama  : Tedi Veradino

NPM  : 1906379131

Angkatan : 2019

TTL  : Biaro, 15 Juli 2000

Asal  : Bukittinggi

Hobi  : voli, nanjak gunung

Perkenalan Singkat

Nama saya adalah Tedi Veradino. Saya merupakan mahasiswa Fakultas Teknik Universitas Indonesia dengan Program Studi S1 Reguler Teknik Mesin. Saya berasal dari Bukittinggi, Sumatera Barat. Saya sangat bersyukur bisa diterima menjadi bagian dari mahasiswa FTUI.

Sebelum UTS saya sudah belajar metnum bersama pa engkos tentang berbagai metode, seperti metode secan, newtom, interpolasi, regresi dan lain-lain.

"Sesungguhnya ilmu yang kita dapat mampu membuat kita mengenal diri kita lebih baik dari sebelumnya"

Tujuan belajar Metode Numerik:

1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik

2. Menerapkan pemahaman yang didapat ke dalam model numerik

3. Mampu menerapkan pemahaman yang didapat ke dalam persoalan teknik

4. Mendapat nilai tambah sehingga menjadi orang yang beradab

Tugas Minggu 1

saya telah mempelajari cara menggunakan open modelica di https://www.youtube.com/watch?v=Dw66ODbMS2A

selain itu saya juga mencoba untuk mengaplikasikannya sendiri di https://youtu.be/HC5NfViuPrg

ringkasan 18/11/2020

Seperti biasa kelas dimulai dengan review materi minggu kemarin terlebih dahulu. kelas pada hari ini juga dihadiri oleh asdos yaitu bang edo. selanjutnya kelas dilanjutkan dengan mempresentasikan tugas minggu kedua. Presentasi tugas ditampilkan oleh beberapa mahasiswa. dalam presentasi tersebut terlihat bergagai macam aplikasi dari openmodelica. ada yang digunakan dalam termodinamika, heat transfer, dan juga CFD. selain ada sesi presentasi, juga ada sesi tanya jawab antara mahasiswa dengan Pak DAI dan juga ada komentar juga dari bang edo.

selain itu Pak DAI juga menjelaskan kelebihan dari openmodelica

1.Dalam Bahasa pemodelan

2.Proses pemahaman intruksi nya cepat

3.Banyak penggunanya

kita juga belajar mandiri yaitu praktek newton rhapson

Tugas Minggu ke 2

Untuk tugas minggu kedua kita diminta Pak DAI untuk membuat sebuah class dan fungsi panggil

Untuk contoh matriknya saya ambil dari internet, sebagai berikut

Tedi Veradino 2-1.png

langkah pertama yaitu kita membuat sebuah class dan input nilai dari matriksnya

Tedi Veradino 2-2.png

selanjutnya yaitu membuat sebuah function

Tedi Veradino 2-3.png

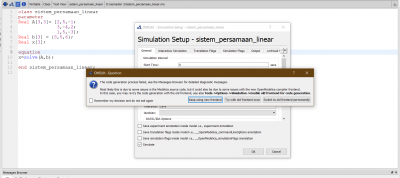
langkah selanjutnya adalah membuat simulation, namun saya memiliki kendala disini.

Tedi Veradino 2-4.png

saya akan mencoba mencari solusinya hingga kelas dimulai. dan jika saya masih belum bisa mungkin bisa didiskusikan di kelas nanti bersama Pak DAI dan teman-teman

Alhamdulillah setelah saya bertanya ke teman-teman saya dapat menyelesaikan kesalahan yang tadi. terima kasih kepada teman-teman terutama kepada Richardo Ariyanto

Berikut video tugas saya dapat dilihat di https://youtu.be/eUdL7SJz3tU

Minggu Ke 3

Setelah uts kita akan banyak mempelajari aplikasi metoda numerik dalam Teknik. Dalam Minggu ini kita diminta Pak DAI untuk belajar persamaan aljabar. kita juga sempat dikusi Variable Rey dengan josiah karena dia terlebih dahulu belajar pada mata kuliah CFD. Meriview Kembali eliminas Gauss

Untuk tugas hari ini Menyelesaikan persamaan 9.12 Latihan membuat fungsi modelica

Naive Gauss

Naivegausstedi.png

function NaiveGauss dari buku Chapra

/* // Pseudocode Figure 9.4

//Forward Elimination DOFOR k = 1, n - 1 

 DOFOR i = k + 1, n
   factor = a[i,k] / a[k,k]
   DOFOR j = k + 1 to n
     a[i,j] = a[i,j] - factor * a[k,j]
   END DO
   b[i] = b[i] - factor * b[k]
 END DO

END DO

// Back Substitution x[n] = b[n] / a[n,n] DOFOR i = n - 1, 1, -1 

 sum = b[i]
 DOFOR j = i + 1, n
   sum = sum = a[i,j] * x[j]
 END DO
 x[i] = sum / a[i,i]

END DO

  • /


Tugas Minggu Ke 3

TRUSS

Truss adalah struktur teknik yang terdiri dari anggota lurus yang terhubung pada mereka diakhiri dengan baut, paku keling, pin, atau pengelasan. Anggota yang ditemukan dalam rangka dapat terdiri dari tabung baja atau aluminium, penyangga kayu, batang logam, sudut, dan saluran. Gulungan menawarkan solusi praktis untuk banyak masalah struktural di bidang teknik, seperti tenaga menara transmisi, jembatan, dan atap gedung. Rangka pesawat didefinisikan sebagai rangka yang anggotanya terbaring di satu pesawat. Gaya yang bekerja pada rangka seperti itu juga harus berada pesawat ini. Anggota rangka umumnya dianggap anggota dua gaya.

PR Truss

Problem 3 tedi veradino.jpeg

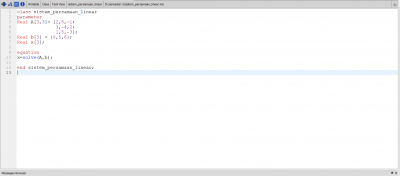
model Trusses 

parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary coundition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];

//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);

G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses;

|}


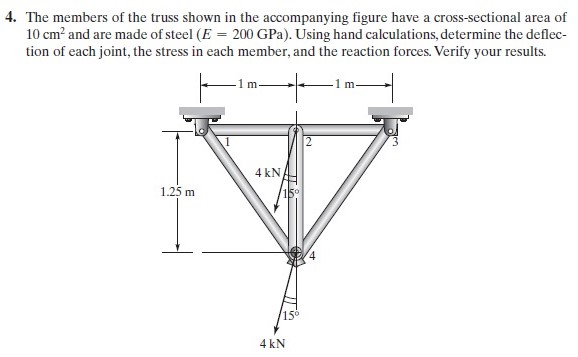
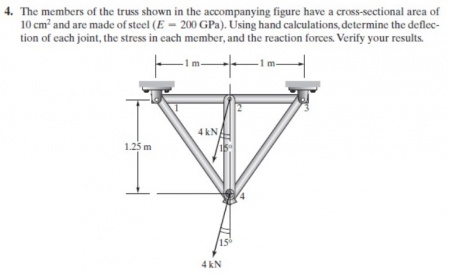
Trusses Problem 2 (Homework)

Soal Trusses 2 fashal.jpg


Discplacement Graphics
Reaction Forces Graphics

Persamaan 

class Trusses_HW

parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary condition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses_HW;

Fungsi Panggil

Matrice Transformation 

function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
    
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness_Matrices;

Global Element Matrice 

function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
 for j in 1:B loop
     G[i,j]:=0;
 end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];

end Local_Global;

Gauss_Jordan 

function Gauss_Jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;

algorithm
X:=Modelica.Math.Matrices.solve(A,B);

for i in 1:N loop
  if abs(X[i]) <= float_error then
    X[i] := 0;
  end if;
end for;

end Gauss_Jordan;

Reaction Matrice Equation 

function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
 if abs(X[i,1]) <= float_error then
   X[i,1] := 0;
 end if;
end for;

for i in 1:N loop
 Sol[i]:=X[i,1];
end for;

end Reaction_Trusses;
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Tedi_Veradino&oldid=45143"