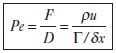Bintang Farhan Muhammad - 1706986334

Di bawah ini tertulis arsip-arsip pembelajaran oleh Bintang Farhan Muhammad

Profil Singkat

Nama : Bintang Farhan Muhammad

NPM  : 1706986334

Skripsi : Korelasi Emission Factor dan Kedalaman Bakar Lahan Gambut

E-mail  : bintang.farhan@ui.ac.id

Persamaan Atur

Fenomena aliran fluida terjadi mengikuti sebuah persamaan matematis, yakni persamaan Navier-Stokes. Persamaan ini ditemukan oleh Navier dan Stokes sejak lebih dari satu abad yang lalu dan masih digunakan hingga kini. Navier-Stokes pada dasarnya merupakan persamaan konservasi yang terdiri dari tiga persamaan diferensial parsial (PDE), yakni persamaan konservasi momentum, konservasi massa, dan konservasi energi.

Konservasi Massa

Jika dianalisa dengan metode Eulerian pada sebuah kontrol volume tanpa keberadaan mass source ataupun sink, massa pada kontrol volume tersebut terkonservasi dalam skala lokal. Artinya, tidak ada perubahan massa yang masuk dan keluar/yang terakumulasi pada kontrol volume tersebut. Disisi lain, secara konvektif, dari satu titik ke titik lainnya tetap bisa jadi terdapat perbedaan besaran massa. Persamaan konservasi massa ditunjukkan pada persamaan pertama pada tabel 1.

Konservasi Momentum

Jika tidak diberikan gaya eksternal, maka sebuah objek akan selalu memiliki momentum yang besarnya konstan, yang merupakan produk dari massa dan kecepatan objek tersebut. Hukum konservasi momentum tersebut juga berlaku pada fluida, seperti yang tertulis pada persamaan ke-2, ke-3, dan ke-4 pada tabel 1 yang masing-masing untuk sumbu x, y, dan z. Dapat dilihat bahwa konservasi momentum dalam aliran fluida secara general akan selalu dipengaruhi oleh faktor eksternal yang tertulis di RHS persamaan tersebut, antara lain tekanan, viskositas, dan sumber lainnya.

Tekanan merupakan main driving force dari keberadaan aliran fluida, dimana fluida mengalir dari daerah bertekanan tinggi ke tekanan rendah. Fakta tersebutlah yang menyebabkan perbedaan tekanan, baik dalam arah sumbu x, y, dan z, menjadi Source term pada persamaan momentum. Tekanan dapat bervariasi terhadap ketinggian maupun disebabkan oleh losses atau adanya energi yang masuk dari mesin-mesin fluida. Selain tekanan, momentum juga dipengaruhi gaya viskos dari fluida tersebut. Seperti yang dipelajari pada mekanika fluida dasar, viskositas merupakan tolak ukur sebuah fluida dalam menolak gerakan (resisting motion). Gaya viskos dalam aliran fluida cendrung membuat fluida tersebut berhenti/diperlambat dan membentuk boundary layer di dekat permukaan. Hal ini memberikan efek terhadap flow regime secara keseluruhan sehingga diperhitungkan dalam konservasi momentum. Dalam kasus aliran fluida, gaya viskos menjadi aspek difusi yang menyebabkan hilangnya momentum. Faktor terakhir merupakan sumber-sumber lainnya, seperti misalnya Buoyancy yang dimasukkan dalam Source term dalam bentuk aproksimasi Boussinesq.

Konservasi Energi

Konservasi energi pada dasarnya menyatakan energi tidak dapat hilang dan hanya dapat berubah bentuk. Dalam kasus aliran fluida, ditunjukkan pada persamaan ke-5 pada tabel 1, yang dipengaruhi kerja yang keluar dan kalor yang masuk, fungsi disipasi, serta Source term, seperti heat generation di dalam kontrol volume atau temperatur di boundary.

Equations of State

Persamaan ini menjelaskan hubungan sebuah skalar, seperti temperatur, tekanan, densitas, dan lain sebagainya, dengan parameter yang bisa memengaruhi regime aliran, seperti persamaan gas ideal atau energi dalam. Misalnya, dalam persamaan gas ideal jika temperatur berubah maka densitas akan berubah sehingga dapat menghasilkan gaya buoyant pada domain aliran.

Tabel 1 Persamaan Atur dalam Fenomena Aliran Fluida Kompresibel Newtonian (Versteeg & Malalasekera, 1995)

Dibawah ini merupakan link video tugas penurunan persamaan momentum dan aplikasinya dalam contoh soal.

Video Penurunan Rumus Momentum

Finite Volume

Berbagai metode komputasi, seperti finite difference, finite element, DEM, dan lain sebagainya, telah dikembangkan dan dapat digunakan untuk menganalisis sebuah sistem dengan cara numerik, tetapi finite volume menjadi pilihan untuk penyelesaian numerikal pada permasalahan CFD. Finite volume merupakan sebuah metode perhitungan yang mengikuti prinsip Eulerian dan menganalisis aliran fluida pada sebuah kontrol volume diskrit yang berkaitan satu dengan yang lainnya. Perhitungan tersebut dilakukan dengan mengintegrasikan PDE melalui sebuah kontrol volume sehingga didapatkan persamaan aljabar yang lebih mudah diselesaikan dan dapat diselesaikan secara komputasi.

Langkah-langkah Pengerjaan Finite Volume

Grid Generation

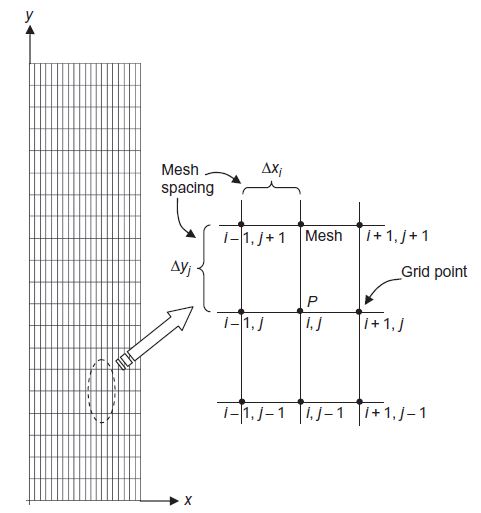
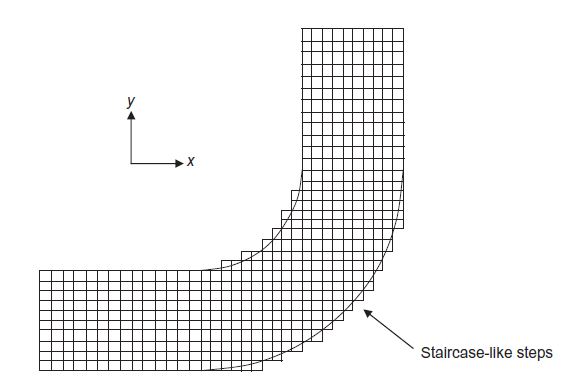
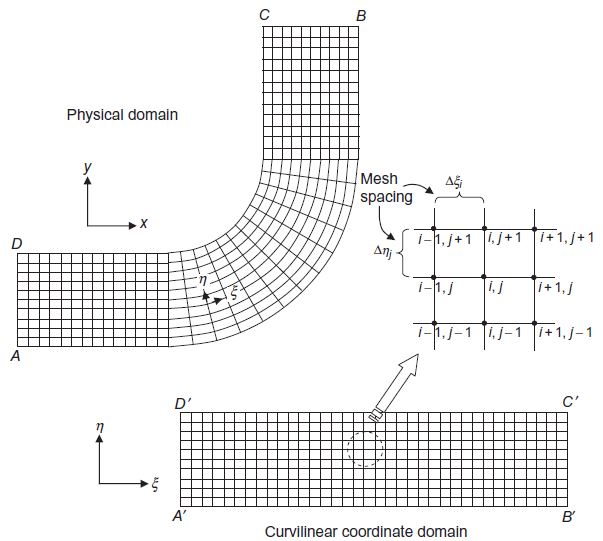
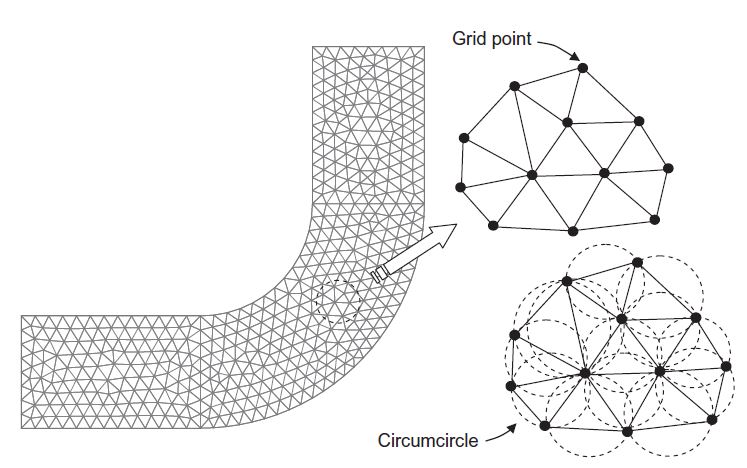
Pembentukan grid merupakan proses membagi domain yang menjadi daerah yang ditinjau menjadi kontrol volume diskrit berukuran kecil. Proses ini juga seringkali disebut dengan meshing. Berbagai jenis mesh/grid perlu diperhatikan penggunaannya sesuai dengan kebutuhan, seperti misalnya dynamic mesh, structured mesh, unstructured mesh, dan body-fitted mesh, yang diperjelas melalui gambar di bawah. Unstructured mesh menjadi yang paling umum digunakan karena fleksibilitasnya dalam mengikut bentuk geometri (Tu et al., 2018). Non-uniform mesh digunakan untuk memperhitungkan efek viskos pada dinding dengan lebih detail ataupun lokasi dimana fenomena aliran lebih difokuskan, terutama di dekat sebuah objek. Bentuk grid paling sederhana adalah kotak, tetapi ada juga bentuk lain seperti polihedral dan triangular.

Sumber gambar : Tu et al., 2018

Gambar 1 Structured mesh uniform (kiri) dan non-uniform (kanan)

Gambar 2 Non-body-fitted structured mesh

Gambar 3 Body-fitted structured mesh

Gambar 4 Triangular

Gambar 5 Polihedral

Diskritisasi & Metode Diskritisasi

Diskritisasi merupakan proses merubah PDE menjadi sistem persamaan linear sehingga dapat diselesaikan dengan lebih mudah secara simultan. Metode-metode yang digunakan dijelaskan di bawah ini.

Central Differencing

Upwind Differencing

Hybrid Differencing

QUICK

TVD

Penyelesaian

Setelah didapatkan sistem persamaan linear, nilai properties pada tiap-tiap nodal dapat dihitung secara simultan. Jika jumlahnya sedikit biasanya sistem persamaan disusun dalam bentuk matriks dan dapat diselesaikan dengan metode Gauss-Jordan. Namun, tentunya jika memenuhi grid independence jumlah nodal akan sangat banyak dan diselesaikan melalui komputer.

Aspek Penentu Kualitas Simulasi

Ada beberapa aspek yang perlu diperhatikan dalam proses diskritisasi dan grid generation, yakni grid independence, boundedness, transportiveness, serta efek konvektif dari aliran yang ditinjau melalui bilangan Peclet. Aspek-aspek tersebut akan dijelaskan dibawah ini:

Grid Independence

Setiap proses diskritisasi dalam kasus perhitungan CFD memiliki error yang disebut dengan truncation error. Metode central differencing memiliki truncation error pada orde ke-2, sementara untuk upwing differencing memiliki error pada orde ke-1. Hal ini mengimplikasikan bahwa besar dari satu volume diskrit akan menentukan nilai error yang dihasilkan pada sebuah perhitungan. Berdasarkan fakta tersebut, perlu dilakukan studi grid independence pada setiap kasus simulasi CFD. Grid independence merupakan kondisi dimana jika sebuah mesh di-refine, hasil simulasi sebelum dan setelah di-refine tidak memiliki perbedaan yang signifikan (Tu et al., 2018). Kondisi inilah yang disebut dengan grid independence yang menjadi indikasi bahwa hasil simulasi tersebut sudah baik. Jika ditemukan bahwa hasil simulasi masih berbeda secara signifikan maka mesh perlu di-refine kembali.

Boundedness

Boundedness merupakan persyaratan dimana nilai pada sebuah nodal berada diantara nilai-nilai yang menyelubungi domain aliran, yakni kondisi pada boundary. Hal yang mudah dipantau untuk memastikan boundedness adalah semua koefisien pada nodal yang ditinjau memiliki besaran yang seluruhnya positif atau seluruhnya negatif, tetapi yang sering ditemukan adalah seluruhnya positif.

Transportiveness

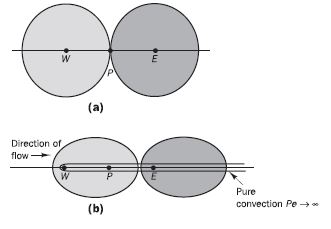
Gambar 5 Ilustrasi efek konvektif dan difusi terhadap aliran (Versteeg & Malalasekera, 1995)

Pada sebuah kasus aliran dimana efek konvektif lebih dominan daripada difusi, transportasi properties pada domain aliran tersebut mengalami pergeseran searah dengan arah aliran. Hal ini disebut dengan transportiveness. Dalam mengukur seberapa besar efek konvektif relatif terhadap difusi digunakan bilangan Peclet yang dirumuskan dengan F/D (Pe = F/D).

Conservativeness

Sesuai dengan namanya, conservativeness pada simulasi mengharuskan fluks yang masuk pada sebuah volume diskrit sama dengan fluks yang keluar. Hal ini dapat terpenuhi jika ekspresi persamaan pada satu nodal dengan nodal lain memiliki susunan yang konsisten sehingga jika disusun ulang akan menghasilkan hasil yang sama, menjadi keseimbangan fluks antar boundary

Dibawah ini merupakan video pengerjaan latihan soal kasus difusi 1D menggunakan finite volume

Video Finite Volume 1D untuk Kasus Difusi

Verifikasi dan Validasi

Verifikasi adalah menyelesaikan persamaan atur dengan benar (tdk ada kesalahan numerik)

Validasi menyelesaikan persamaan atur (termasuk asumsi model math, properties dan boundaru cond) yang benar (faktual)

Dynamic Mesh & 6DoF

                                                             v dot = Sigma F/m

                                                           omega dot = Sigma M/I

Dua persamaan diatas merupakan governing equation dari sebuah geometri yang bergerak secara translasi dan rotasi. Seringkali dalam kasus perhitungan CFD melibatkan boundary yang bergerak. Kasus seperti ini dapat ditemukan juga di internal combustion engine (pergerakan piston dalam engine block), ataupun stator dan rotor pada mesin kerja atau mesin tenaga fluida. Kasus-kasus tersebut melibatkan pergerakan 6DoF, dimana tidak hanya ada translasi pada sumbu x, y, dan z, tetapi juga rotasi terhadap sumbu-sumbu tersebut yang disebut sebagai pitch, yaw, dan roll. Untuk melakukan perhitungan simulasi CFD dalam kasus seperti ini dibutuhkan dynamic mesh/grid yang mengikuti pergerakan boundary, seperti sudu turbin, kepala piston, dll.

Dynamic mesh merupakan metode yang digunakan untuk merubah lokasi mesh sesuai dengan pergerakan boundary. Algoritma dari dynamic mesh sendiri mengingat kurvatur dari boundary dan arah pergerakannya sehingga pada iterasi detik selanjutnya dapat diperhitungkan perpindahan tiap-tiap boundary. Tidak semua bagian dalama dynamic mesh ikut bergerak. Dalam contoh kasus mesin kerja dengan rotor dan stator, sebagian boundary akan bergerak mengikuti pergerakkan impeller dan sebagian lainnya akan diam sesuai dengan boundary dari dinding di sekelilingnya. Menurut Jiyuan Tu, meski dinilai cukup sukses, metode dynamic mesh yang berhasil kebanyakan ada pada kasus geometri kompleks dengan aliran inviscid atau geometri sederhana dengan aliran viskos sehingga perlu dikembangkan lebih jauh (Farhat, 2005).

---

Pada tanggal 17 November 2020, kami mahasiswa kelas CFD diberikan tugas untuk mencoba melakukan simulasi dynamic mesh 3DoF (dua dimensi, satu sumbu rotasi) dengan menggunakan CFDSOF tanpa GUI. Kami merubah beberapa parameter pada file dalam simulasi VAWT, yakni file controlDict serta dynamicmeshDict. Beberapa parameter yang saya rubah adalah sebagai berikut:

File dynamicmeshDict

//- Gravitational acceleration if g is used in the calculation //g

File controlDict

application cfdsofpimpleDyM;

startFrom latestTime;

writeInterval 0.01;

endTime 5;

maxDeltaT 0.01;

Meski demikian, simulasi tersebut cukup berat dilakukan pada laptop saya dan tidak dihitung hingga selesai karena laptop panas dan mati dengan sendirinya. Dokumentasi sejauh ini untuk hasil simulasi dapat dilihat pada gambar-gambar di bawah ini:

Gambar 1

Gambar 2

Gambar 3 Pada detik 0.055

Gambar 4 Pada detik 0.21

Dapat dilihat ada pergeseran mesh

CFD Multiphase : Economizer Hopper

Dalam latihan kali ini dilakukan simulasi CFD Economizer Hopper dan perbandingan aliran multifasa tersebut jika tanpa Economizer Hopper. Dapat diperhatikan bahwa dengan Economizer Hopper, partikel hasil pembakaran terperangkap pada Economizer Hopper dan tidak ikut keluar pada bagian outflow sehingga menghasilkan gas buang yang lebih bersih.

Gambar 1 Dengan Economizer Hopper

Gambar 2 Tanpa Economizer Hopper