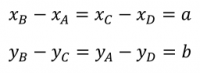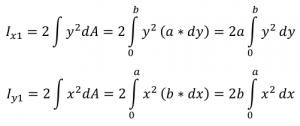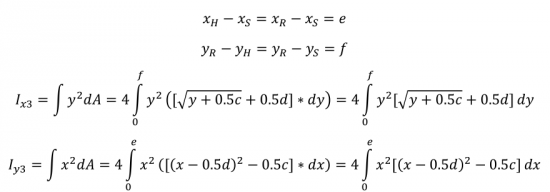Difference between revisions of "Tugas UTS Ismail"
Ismailbagus (talk | contribs) (x) |
Ismailbagus (talk | contribs) |
||
| Line 31: | Line 31: | ||
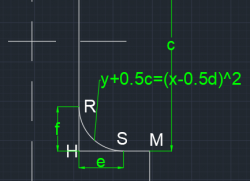
Bagian 3 memiliki bentuk berupa fungsi f(x) = (x-0.5d)<sup>2</sup> - 0.5c dari titik x<sub>H</sub> ke x<sub>S</sub> dan y<sub>R</sub> ke y<sub>H</sub>. Selain balok HRS, balok yang juga merupakan bagian 3 adalah balok GTU, EPQ dan FNO. Perumusan untuk inersia ke arah x (I<sub>x</sub>) dan inersia ke arah y (I<sub>y</sub>) pada bagian 3 adalah: | Bagian 3 memiliki bentuk berupa fungsi f(x) = (x-0.5d)<sup>2</sup> - 0.5c dari titik x<sub>H</sub> ke x<sub>S</sub> dan y<sub>R</sub> ke y<sub>H</sub>. Selain balok HRS, balok yang juga merupakan bagian 3 adalah balok GTU, EPQ dan FNO. Perumusan untuk inersia ke arah x (I<sub>x</sub>) dan inersia ke arah y (I<sub>y</sub>) pada bagian 3 adalah: | ||
| − | [[File:SumatraPDF_2019-04-05_23-29-53.png|center| | + | [[File:SumatraPDF_2019-04-05_23-29-53.png|center|550px]] |
</div> | </div> | ||
---- | ---- | ||
===Total=== | ===Total=== | ||
---- | ---- | ||
| − | + | Setelah dicari inersia untuk tiap bagian, kemudian inersia dijumlah sehingga nilai I<sub>x</sub> dan I<sub>y</sub> untuk gambar 1 adalah: | |
| + | [[File:SumatraPDF_2019-04-05_23-32-00.png|center|150px]] | ||
---- | ---- | ||
Revision as of 23:33, 5 April 2019
Contents
[hide]Tugas UTS
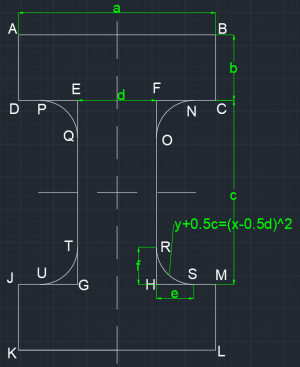
Akan dicari inersia ke arah x (I x ) dan inersia ke arah y (I y ) untuk sebuah permukaan benda di gambar 1. Untuk mencari inersia tersebut, benda dibagi menjadi beberapa bagian. Hal tersebut dikarenakan inersia bersifat skalar sehingga hasil dapat dihitung dengan artimatika biasa. Bagian-bagian yang dihitung adalah:
Bagian 1
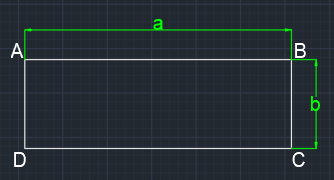
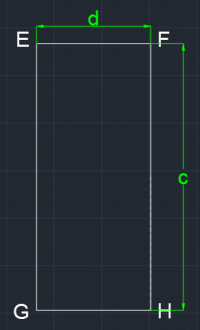
Bagian 1 memiliki bentuk persegi panjang dengan luas a x b. Selain balok ABCD, balok yang juga merupakan bagian I adalah balok JKLM. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 1 adalah:
Bagian 2
Bagian 2 memiliki bentuk persegi panjang dengan luas c x d. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 2 adalah:
Bagian 3
Bagian 3 memiliki bentuk berupa fungsi f(x) = (x-0.5d)2 - 0.5c dari titik xH ke xS dan yR ke yH. Selain balok HRS, balok yang juga merupakan bagian 3 adalah balok GTU, EPQ dan FNO. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 3 adalah:
Total
Setelah dicari inersia untuk tiap bagian, kemudian inersia dijumlah sehingga nilai Ix dan Iy untuk gambar 1 adalah: