Difference between revisions of "Tri Aji Setyawan"
(→MINGGU KE 3) |
(→MINGGU KE 3) |
||
| Line 38: | Line 38: | ||
*pseudocode figure 9.4 | *pseudocode figure 9.4 | ||
[[File:Pseudocode.jpg|600px|center]] | [[File:Pseudocode.jpg|600px|center]] | ||
| + | |||
| − | + | input Real [:,:] A; // Left-hand Coefficients of the Linear Equation System in array form | |
| − | + | input Real [:] B; // Right-hand Constants of the Linear Equation System in array form | |
| − | input Real [:,:] A; | + | output Real [:,:] y;// Array containing coefficient matrix after NGE operation |
| − | input Real [:] B; | + | output Real [:] x; // Array containing solved values of x |
| − | output Real [:,:] y; | ||
| − | output Real [:] x; | ||
protected | protected | ||
Real [:,:] a; | Real [:,:] a; | ||
Real [:] b; | Real [:] b; | ||
| − | Integer m = size(A,1); // | + | Integer m = size(A,1); // Number of rows in matrix |
| − | Integer n = size(A,2); // | + | Integer n = size(A,2); // Number of columns in matrix |
| − | Real k = 1; | + | Real k = 1; // Pivot column pointer |
| − | Real i = 1; | + | Real i = 1; // Row counter |
| − | Real j = 1; | + | Real j = 1; // Row element counter |
| − | Real factor = 1; | + | Real factor = 1; // Factor value used for forward elimination |
| − | Real sum = 1; | + | Real sum = 1; // Sum value used for back substitution |
algorithm | algorithm | ||
| + | // Transfer input matrix (A,B) into variables (a,b) | ||
a := A; | a := A; | ||
b := B; | b := B; | ||
| Line 83: | Line 83: | ||
end for; | end for; | ||
| − | end | + | end NaiveGauss; |
| + | |||
| + | </syntaxhighlight> | ||
Revision as of 07:55, 2 December 2020
Biodata
Tri Aji Setyawan 1906301324
Saya merupakan mahasiswa teknik mesin UI angkatan 2019. saya menyukai teknik mesin karena tertarik pada bidang manufaktur dan karena teknik mesin sendiri memiliki prospek kerja yang luas. hal yang saya pelajari sebelum uts ini adalah mengenai turunan numerik, deret mclaurin , interpolasi, regresi, pengertian dari metode numerik, pseucode.
MINGGU KE 1
- Tujuan mempelajari metode numerik
- 1. matching dengan tujuan belajar: memahami konsep dan prinsip dasar di dalam metnum. contoh persamaan aljabar, algorithma, pencocokan kurva, persamaan diferensial parsial.
- 2. dapat menerapkan pemahaman terhadap konsep di dalam permodelan numerik ( pengaplikasian metode numerik )
- 3. mampu menerapkan metnum di dalam persoalan keteknikan.
- 4. untuk mencapai poin 1,2,3, yaitu dengan cara moral value (adab). untuk menambah nilai tambah / adabsehingga kita menjadi orang yang lebih beradab
TUGAS 1
Pada pertemuan sebelumnya , saya mendapatkan tugas untuk membuat video terkait penggunaan aplikasi open modelica
MINGGU KE 2
Tugas 2
MINGGU KE 3
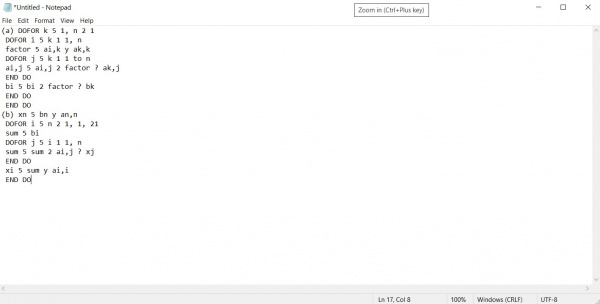
- pseudocode figure 9.4
input Real [:,:] A; // Left-hand Coefficients of the Linear Equation System in array form
input Real [:] B; // Right-hand Constants of the Linear Equation System in array form
output Real [:,:] y;// Array containing coefficient matrix after NGE operation
output Real [:] x; // Array containing solved values of x
protected Real [:,:] a; Real [:] b; Integer m = size(A,1); // Number of rows in matrix Integer n = size(A,2); // Number of columns in matrix Real k = 1; // Pivot column pointer Real i = 1; // Row counter Real j = 1; // Row element counter Real factor = 1; // Factor value used for forward elimination Real sum = 1; // Sum value used for back substitution
algorithm
// Transfer input matrix (A,B) into variables (a,b) a := A; b := B;
// Forward Elimination for k in 1:(n-1) loop
for i in (k+1):n loop
factor := a[i,k] / a[k,k];
for j in (k+1):n loop
a[i,j] := a[i,j] - (factor * a[k,j]);
end for;
b[i] := b[i] - (factor * b[k]);
end for;
end for;
// Back Substitution x[n] := b[n] / a[n,n]; for i in (n-1):(-1) loop
sum := b[i]; for j in (i+1):n loop sum := sum - (a[i,j] * x[j]); end for; x[i] := sum / a[i,i];
end for;
end NaiveGauss;
</syntaxhighlight>