Difference between revisions of "Muhamad Ilham Santoso"
| Line 372: | Line 372: | ||
| − | + | [[File:Metode2RK.png]] | |
Revision as of 15:26, 6 November 2019
Hello Everyone!
Nama : Muhamad Ilham Santoso
NPM : 1706986422
Assalamu'alaykum Wr. Wb.
Mengapa kita sebagai mahasiswa teknik mesin perlu mempelajari mata kuliah Kalkulus? Kalkulus merupakan salah satu mata kuliah dasar yang berfungsi sebagai fondasi untuk mempelajari mata kuliah lain. Sebagai seorang calon sarjana teknik mesin, harus memahami konsep mata kuliah Kalkulus agar mampu menganalisis,memodelkan, dan mensimulasikan suatu sistem yang ada untuk mendapatkan pemecahan masalah.
Contents
- 1 Pertemuan Pertama Mata Kuliah Metode Numerik
- 2 Pertemuan Kedua Mata Kuliah Metode Numerik
- 3 Pertemuan Ketiga Mata Kuliah Metode Numerik
- 4 Pertemuan Keempat Mata Kuliah Metode Numerik
- 5 Pertemuan Kelima Mata Kuliah Metode Numerik
- 6 Pertemuan Keenam Mata Kuliah Metode Numerik
- 7 Pertemuan Keenam Mata Kuliah Metode Numerik
- 8 REVISI UTS 29 OKTOBER 2019
- 9 System for smooth sphere with drag in two directions (Runge Kutta Method)
Pertemuan Pertama Mata Kuliah Metode Numerik
Waktu : Rabu, 4 September 2019
Oleh : Dr. Eng. Radon Dhelika B.Eng., M.Eng.
- Dr. Ir. Ahmad Indra Siswantara
Pada pertemuan pertama,mata kuliah metode numerik diisi oleh pak Dr. Ir. Ahmad Indra Siswantara atau dan Dr. Eng. Radon Dhelika. Dr. Ir. Ahmad Indra Siswantara atau yang biasa dikenal Pak Dai mengawali perkuliahan dengan memberikan penjelasan singkat tentang mata kuliah metode numerik dan mengenalkan kepada para mahasiswa website air.eng.ui.ac.id. Beliau memberikan reminder bahwa kita tidak boleh lupa berdoa setiap sebelum memulai belajar . Pak Dai memberikan pertanyaan kepada kami “Mengapa mahasiswa teknik mesin harus belajar kalkulus?” dan beliau meminta kami menjawabnya pada laman akun masing-masing. Beliau memberikan alasan bahwa kita harus mempelajari kalkulus karena berguna untuk menurunkan rumus dan juga untuk pemodelan matematika yang akan digunakan pada mata kuliah Teknik mesin seperti termodinamika,pengendalian system,dll.
Metode Numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematika sehingga dapat dipecahkan dengan operasi perhitungan biasa (tambah, kurang, kali, bagi)
Berdasarkan informasi yang didapatkan dari internet, Python adalah bahasa pemrograman interpretatif multiguna yang memakai filosofi perancangan dengan fokus kepada tingkat keterbacaan kode. Sebagai bahasa pemrograman, Python menggabungkan kemampuan, kapabilitas dan sintaksis kode serta fungsi pustaka yang berkualitas tinggi.
Tugas 2: *Mempelajari Python *Memecahkan soal limit (x^2 - 1)/(x - 1) *Contoh aplikasi dari metode numerik
METODE NUMERIK & PYTHON
________________________________________
1. Dalam pemecahan soal yang diberikan yaitu limit (x^2 - 1)/(x - 1) menggunakan bantuan modul Sympy Library dengan mengetik ‘Pip 3 install sympy’ pada di command prompt windows.
Penggunaan Sympy Library memberikan kemudahan untuk melakukan koding yang perlu ditulis.
2.Pengisian pada:
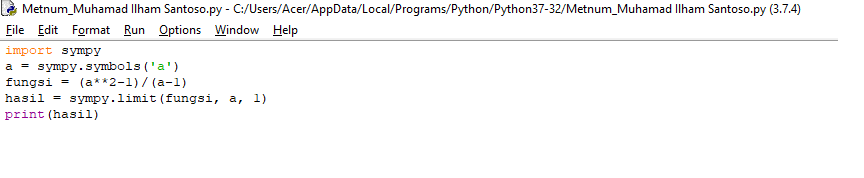
Line 1: " import sympy" untuk melakukan impor modul sympy.
Line 2: "a = sympy.symbols('a')" untuk menetapkan a sebagai simbol yang ada di sympy
Line 3: "fungsi = (a**2-1)/(a-1)" untuk menyimpan perhitungan di variabel fungsi.
Line 4: "hasil = sympy.limit(fungsi, a, 1)" untuk menyimpan hasil perhitungan di variabel hasil.
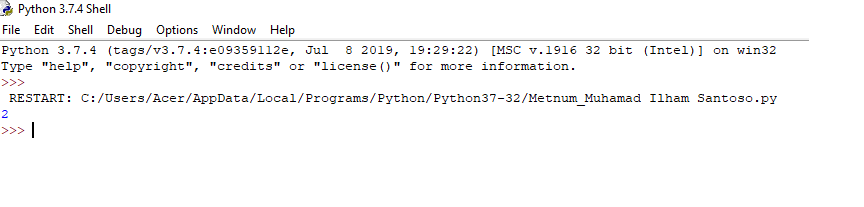
Line 5 : "print(hasil)" perintah yang bertujjuan mencetak jawaban dari persamaan tersebut. Jawaban yang didapatkan adalah 2
Pertemuan Kedua Mata Kuliah Metode Numerik
Waktu : Rabu, 11 September 2019
Memasuki revolusi industri 4.0, semua kalangan seakan-akan dituntut untuk mengenal teknologi lebih dalam. Terlebih lagi, sebagai calon sarjana teknik mesin harus memahami hal-hal tentang device yang mendukung adaptasi untuk menghadapi revolusi industri 4.0 dengan baik. Kapabilitas dan daya tampung otak manusia tidak akan cukup menyimpan dan mengingat seluruh informasi yang tersedia saat ini. Oleh sebab itu, komputer diciptakan mengingat, mengolah data-data dan informasi, dan dapat membantu segala hal yang berhubungan dengan kegiatan manusia khusunya dalam bidang keteknikan. Sampai saat ini sudah berkempang sangat pesat, mulai dari software maupun hardware. Komputer zaman dahulu masih 32bit, namun yang sekarang sudah banyak beredar ialah versi 64bit, dimana besarnya bit ini merepresentasikan kecepatan dalam mengolah data.
Pertemuan Ketiga Mata Kuliah Metode Numerik
Waktu : Rabu, 18 September 2019
Agenda pada pertemuan ketiga yaitu kuis. Soal yang diberikan yaitu sebuah baris yang berisikan angka 1,1,2,3,5,8,13,21,...,n. Pada kuis sesi-1 Kami diberikan soal untuk membuat algoritma, flow chart,dan instruksi pada python. Ketika melihat soal, sontak seluruh isi kelas tercengang karena soal yang dikeluarkan berupa fibonacci. Karena sebagian besar mahasiswa di kelas tidak dapat mengerjakannya, akhirnya dilakukan kuis sesi-2 untuk memperbaikinya. Namun, kali ini diperbolehkan untuk berdiskusi dengan teman-teman yang lain. Intruksi pada kuis sesi-2 yaitu untuk menyelesaikan baris tersebut dengan metode loop while atau for dan function.
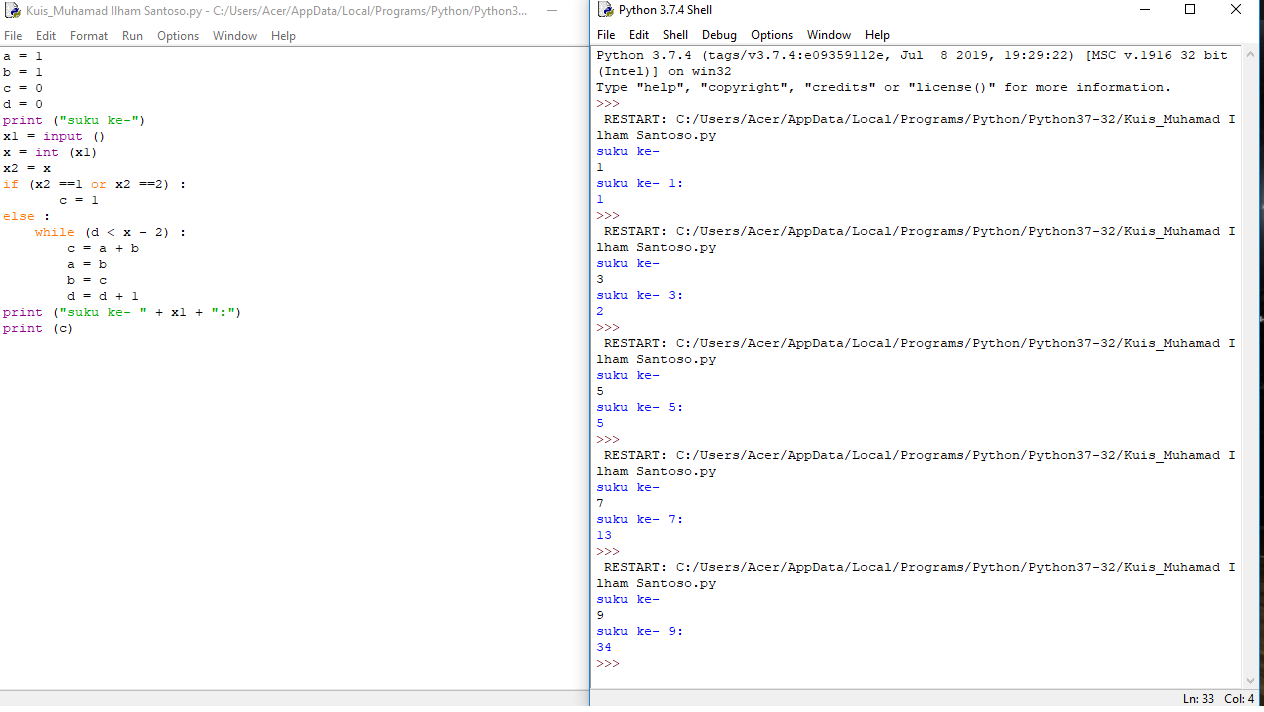
Flow Chart metode loop while
1. Mendefinisikan bilangan Fibonacci
2. Menentukann bilangan awal a=1 ; b=1 ; c=0 ; d=0
3. Menentukan fungsi fibonacci
4. Print Hasil dari suku ke-n yang diinginkan
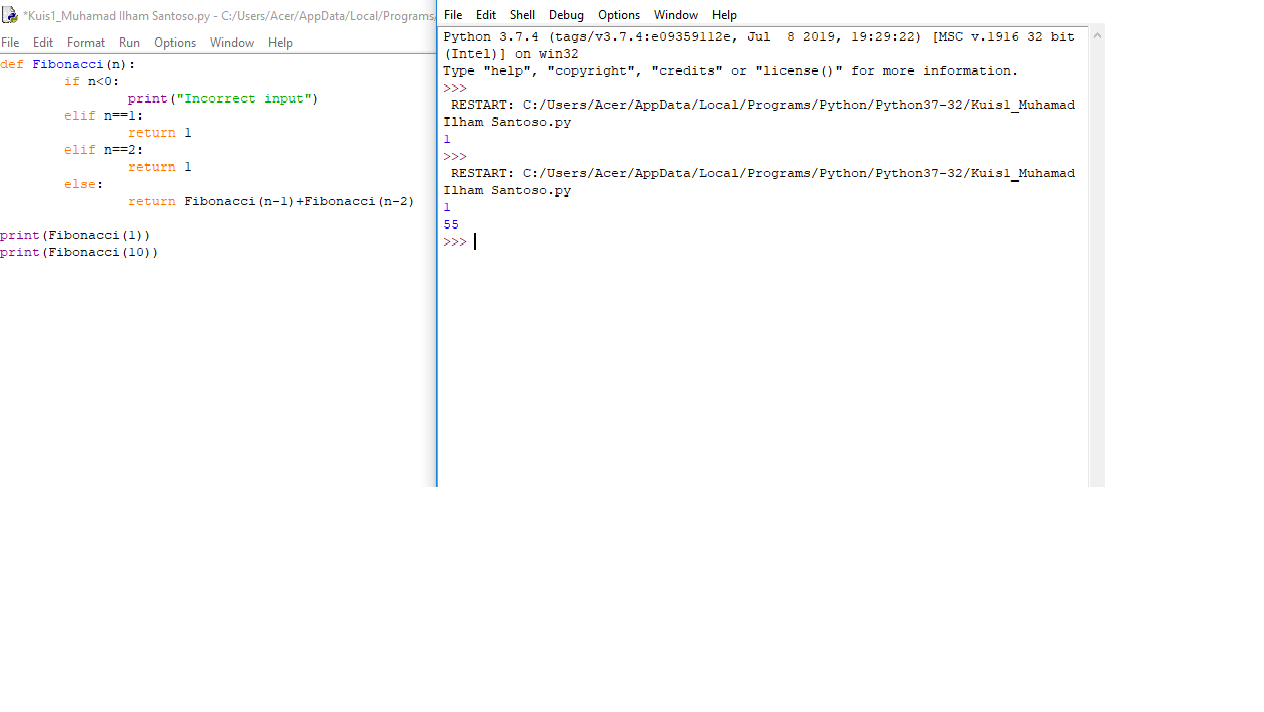
Flow Chart metode function
1. Mendefinisikan bilangan Fibonacci
2. Menentukan batas return
3. Print Hasil dari suku ke-n yang diinginkan
Pertemuan Keempat Mata Kuliah Metode Numerik
Waktu : Rabu, 25 September 2019
Oleh : Dr. Eng. Radon Dhelika B.Eng., M.Eng.
- Dr. Ir. Ahmad Indra Siswantara
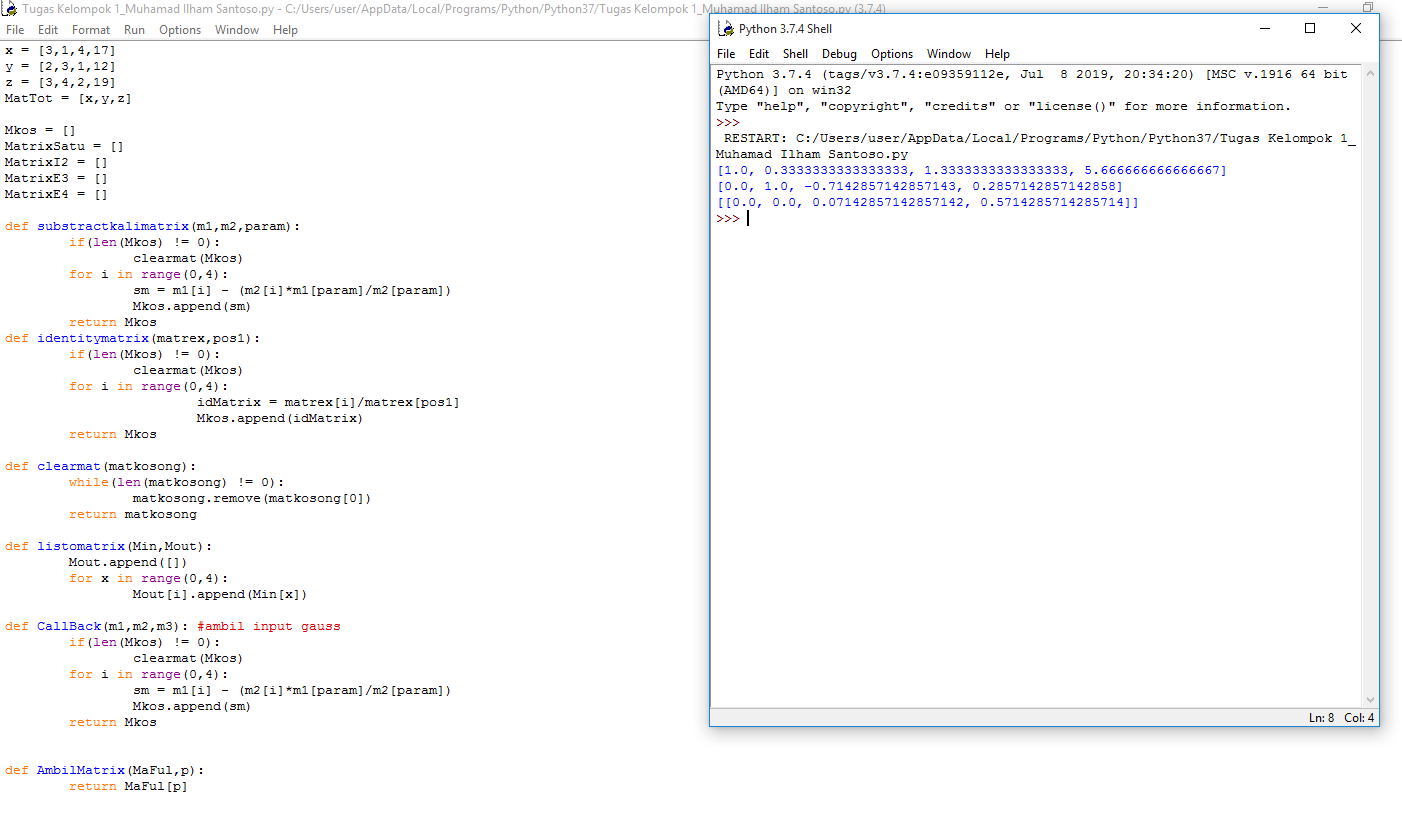
Pada pertemuan keempat,kami diberi tugas untuk membuat sebuah program python yang dapat menjawab soal eliminasi Gauss sebuh matriks. Eliminasi gauss dapat dimanfaatkan untuk memecahkan sistem persamaan linear dengan merepresentasikan (mengubah) menjadi bentuk matriks, matriks tersebut lalu diubah kebentuk Eselon Baris melalui Operasi Baris Elementer. Kemudian sistem diselesaikan dengan substitusi balik. Pada proses pemecahan dengan metode eliminasi gauss pada umumnya memiliki macam-macam jalur atau alur operasi yang dilakukan, misalkan pada langkah awal bisa saja kita menemukan beberapa operasi alternatif dan kita bebas memilihnya.
Eliminasi Gauss-Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana lagi. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks.
Pertemuan Kelima Mata Kuliah Metode Numerik
Waktu : Rabu, 9 Oktober 2019
Oleh : Dr. Eng. Radon Dhelika B.Eng., M.Eng.
- Dr. Ir. Ahmad Indra Siswantara
Setiap permasalahan dapat dimodelkan karena pemodelan mempermudah manusia dalam menyelesaikan suatu permasalahan. Salah satu tools yang dapat digunakan yaitu dengan bahasa pemrograman Python.
Alasan penggunaan Python untuk dijadikan opsi utama dalam menyelesaikan masalah yaitu karena gratis sehingga mudah didapatkan dan saat ini sering digunakan dalam industry 4.0. Selain mudah didapatkan dari internet, Pyhthon juga mudah untuk dipelajari.
Pada pertemuan ini diisi oleh asisten dosen dan mempelajari tentang Aplikasi Aljabar yang akan dimodelkan pada Sistem Pegas. Materi ini berkaitan dengan Finite Element Method (FEM).
Kemudian asisten dosen menjelaskan tentang penggunaan pemodelan pada sistem sunggal menjadi sebuah persamaan linier dengan menerjemahkan rumus yang biasa digunakan pada materi Pegas menjadi sebuah Matrix. Variasi yang digunakan tidak hanya untuk matrix pegas yang tunggal melainkan juga pemodelan sistem ganda pada pegas seri dengan menggunakan superposisi matrix.
Modul yang dapat digunakan pada Python yang dapat memudahkan perhitungan Sistem Persamaan Linier yaitu Sympy dan Nymoy
Pertemuan Keenam Mata Kuliah Metode Numerik
Waktu : Rabu, 9 Oktober 2019
Oleh : Dr. Eng. Radon Dhelika B.Eng., M.Eng.
- Dr. Ir. Ahmad Indra Siswantara
Pada pertemuan keenam, Pak Ahmad Indra menjelaskan bahwa teknik penyelesaian aljabar bervariasi, contohnya menggunakan metode eleminasi, gausian, jacobian,dll. Meskipun computer sudah canggih, tapi kita harus mengerti apa yang dilakukan komputer (algoritma) untuk memodelkan dan menyelesaikan permasalahann yang kita modelkan tersebut. Salah satu konsep yang sangat dasar yaitu agar dapat memodelkan barang yang kontinum. Contohnya adalah sebuah meja yang dianggap kontinum, artinya meja tersebut terisi penuh oleh massa. Ketika meja tersebut diberi beban massa oleh tubuh dengan cara duduk di atas meja, system tersebut dapat menghasilkan sebuah persamaan diferensial. Contoh lain yaitu dalam satu ruangan dipenuhi oleh oksigen, maka tidak ada ruang hampa dalam ruangan. Seluruh ruangan dipenuhi oleh oksigen dan kita dapat mengukur Temperature dititik manapun dalam ruangan.
Pertemuan Keenam Mata Kuliah Metode Numerik
Waktu : Rabu, 16 Oktober 2019
Oleh : - Dr. Ir. Ahmad Indra Siswantara
Quiz Problem 2.1 no 6 dan Problem 7.1 no 2
UTS 23 OKTOBER 2019
SOAL 1
from math import*
#memasukkan variabel yang diketahui
g=9.81
m1=eval(input("massa 1 : "))
m2=eval(input("massa 2 : "))
m3=eval(input("massa 3 : "))
teta=eval(input("sudut: "))
ms=eval(input("koefisien gesek: "))
a=sin(teta)
b=cos(teta)
c=(y-ms*x)
T1=m1*g*c
T2=T1+m2*g*c
T3=T2+m3*g*c
m4=T3/g
print("Tegangan tali 1")
print("Tegangan tali 2")
print("Tegangan tali 3")
SOAL 2
from math import* #input variabel-variabel yang diketahui g = 9.81 pro = 1.2 cd = eval(input("drag coefficient: ")) area = eval (input("area(m^2): ")) m = (input("massa(kg): ")) a = (input("percepatan(m/s^2: ")) u = (input("koefisien gesek: ")) vo = (input("velocity: ")) t = (input("waktu dari diam ke gerak (s): "))
fdrag=(cd*vt**(3/2))/m
f1 = a
atot= ft-fdrag
t=(vt-v0)/atot
print("waktu yang dibutuhkan untuk mencapai kecepatan maksimum")
REVISI UTS 29 OKTOBER 2019
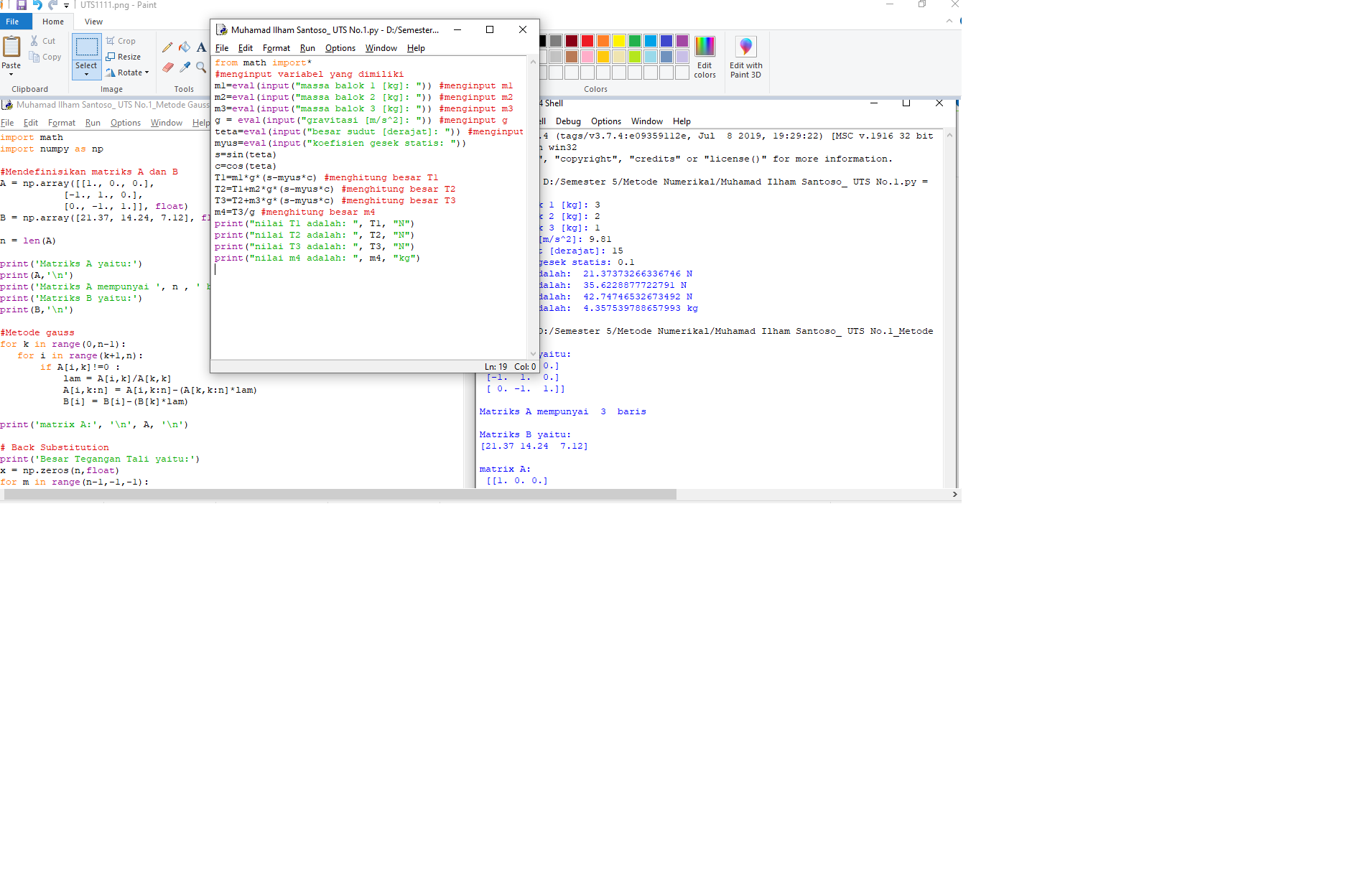
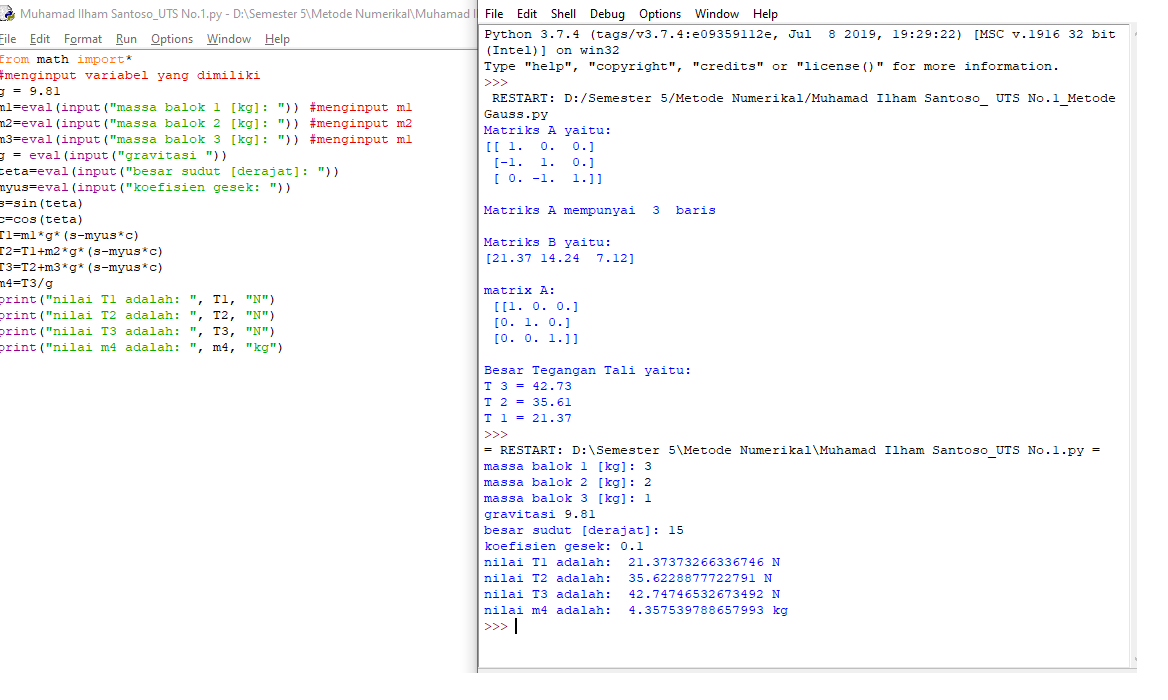
Cara 1 : Penyelesaian dengan Persamaan Fisika
from math import*
#menginput variabel yang dimiliki
g = 9.81
m1=eval(input("massa balok 1 [kg]: ")) #menginput m1
m2=eval(input("massa balok 2 [kg]: ")) #menginput m2
m3=eval(input("massa balok 3 [kg]: ")) #menginput m1
g = eval(input("gravitasi "))
teta=eval(input("besar sudut [derajat]: "))
myus=eval(input("koefisien gesek: "))
s=sin(teta)
c=cos(teta)
T1=m1*g*(s-myus*c)
T2=T1+m2*g*(s-myus*c)
T3=T2+m3*g*(s-myus*c)
m4=T3/g
print("nilai T1 adalah: ", T1, "N")
print("nilai T2 adalah: ", T2, "N")
print("nilai T3 adalah: ", T3, "N")
print("nilai m4 adalah: ", m4, "kg")
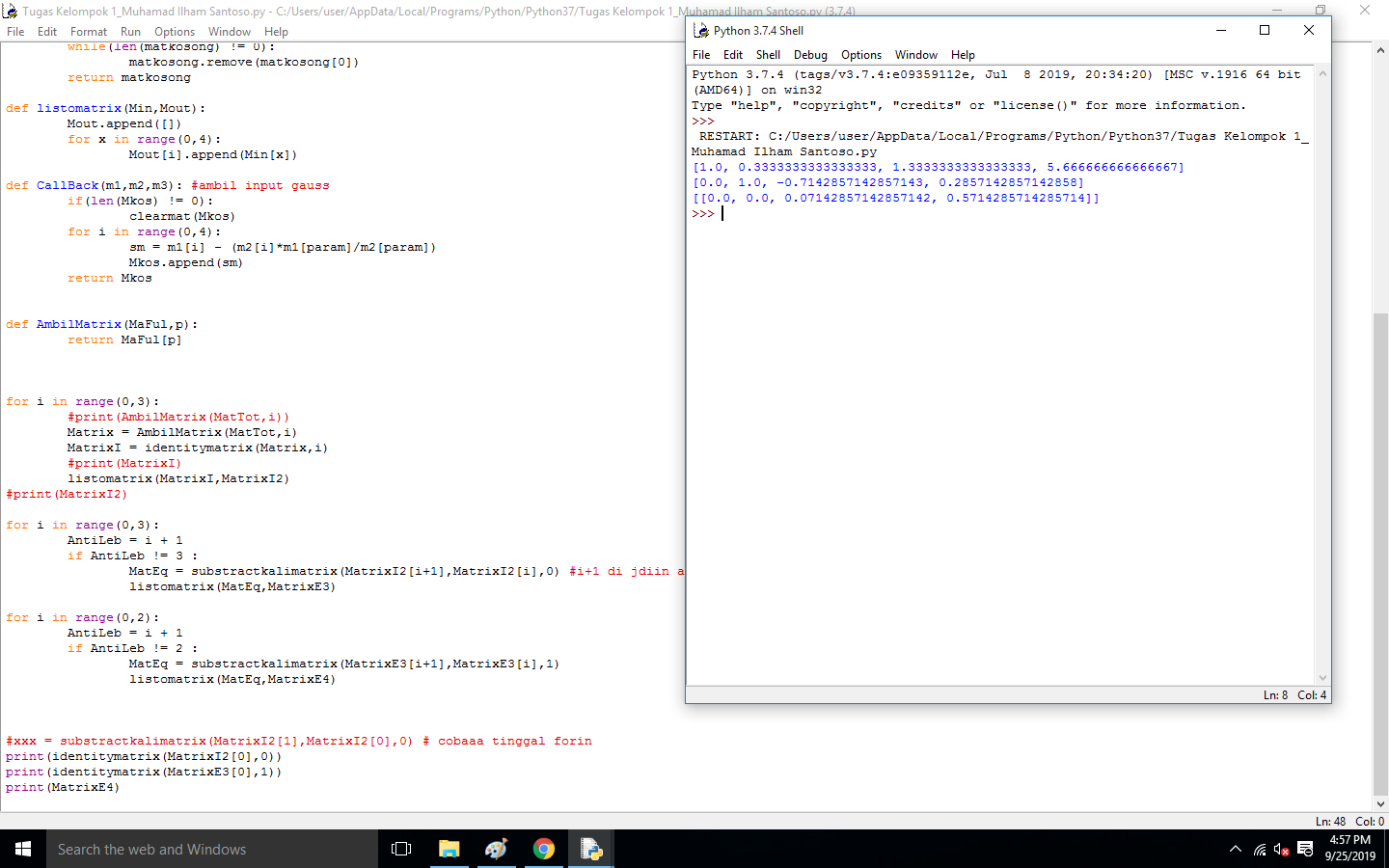
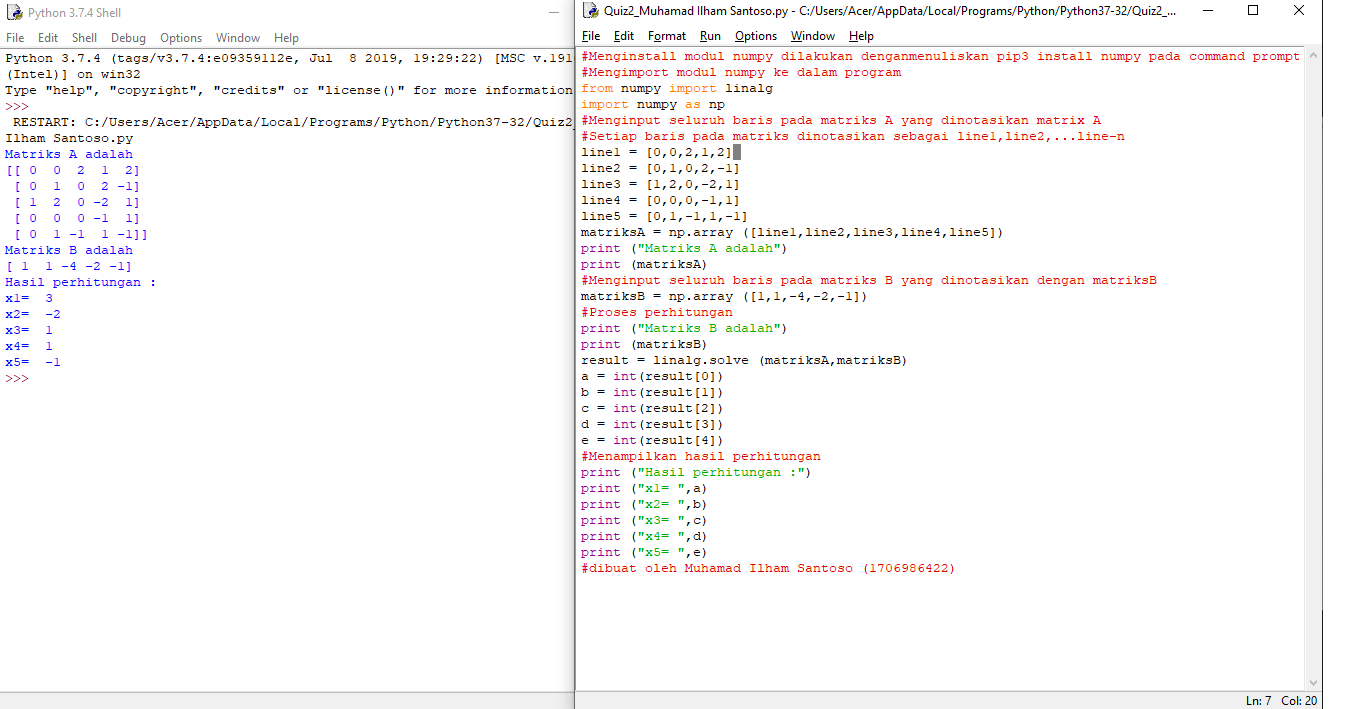
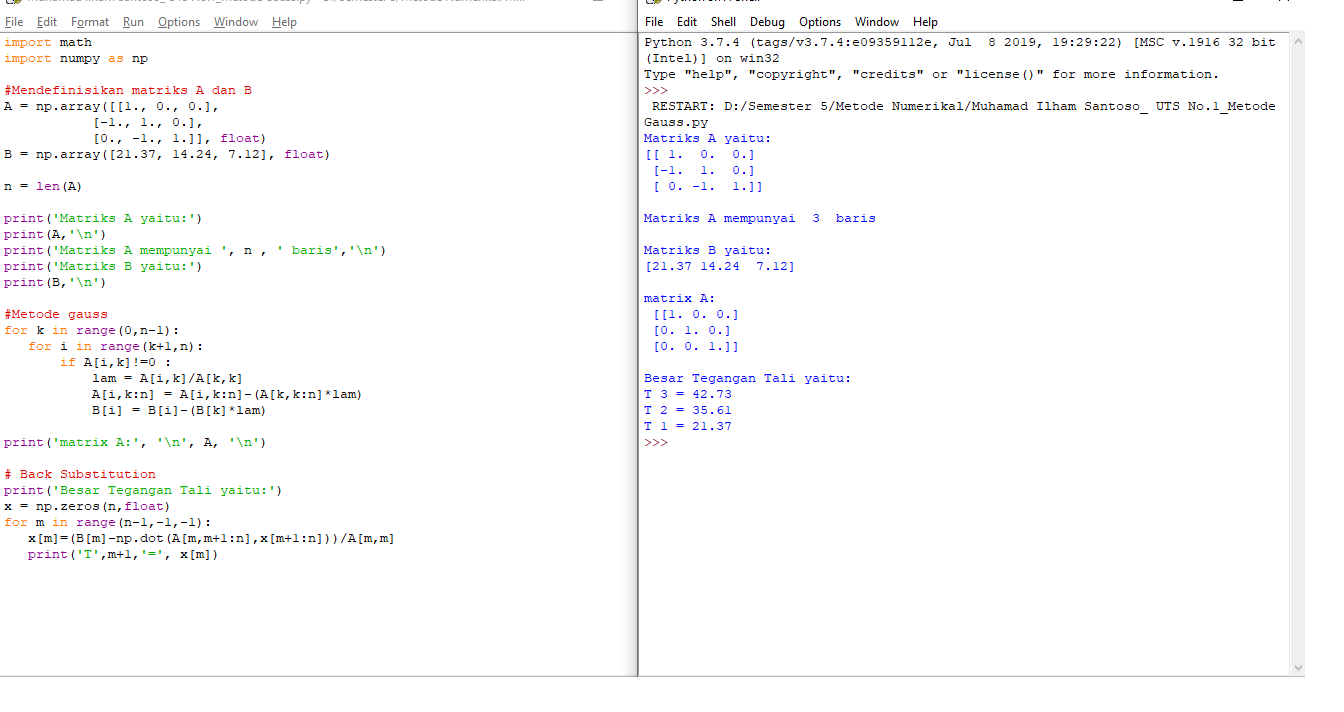
Cara 2 : Eleminasi Gauss
import math import numpy as np
#Mendefinisikan matriks A dan B
A = np.array([[1., 0., 0.],
[-1., 1., 0.],
[0., -1., 1.]], float)
B = np.array([21.37, 14.24, 7.12], float)
n = len(A)
print('Matriks A yaitu:')
print(A,'\n')
print('Matriks A mempunyai ', n , ' baris','\n')
print('Matriks B yaitu:')
print(B,'\n')
#Metode gauss
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
print('matrix A:', '\n', A, '\n')
# Back Substitution
print('Besar Tegangan Tali yaitu:')
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
print('T',m+1,'=', x[m])
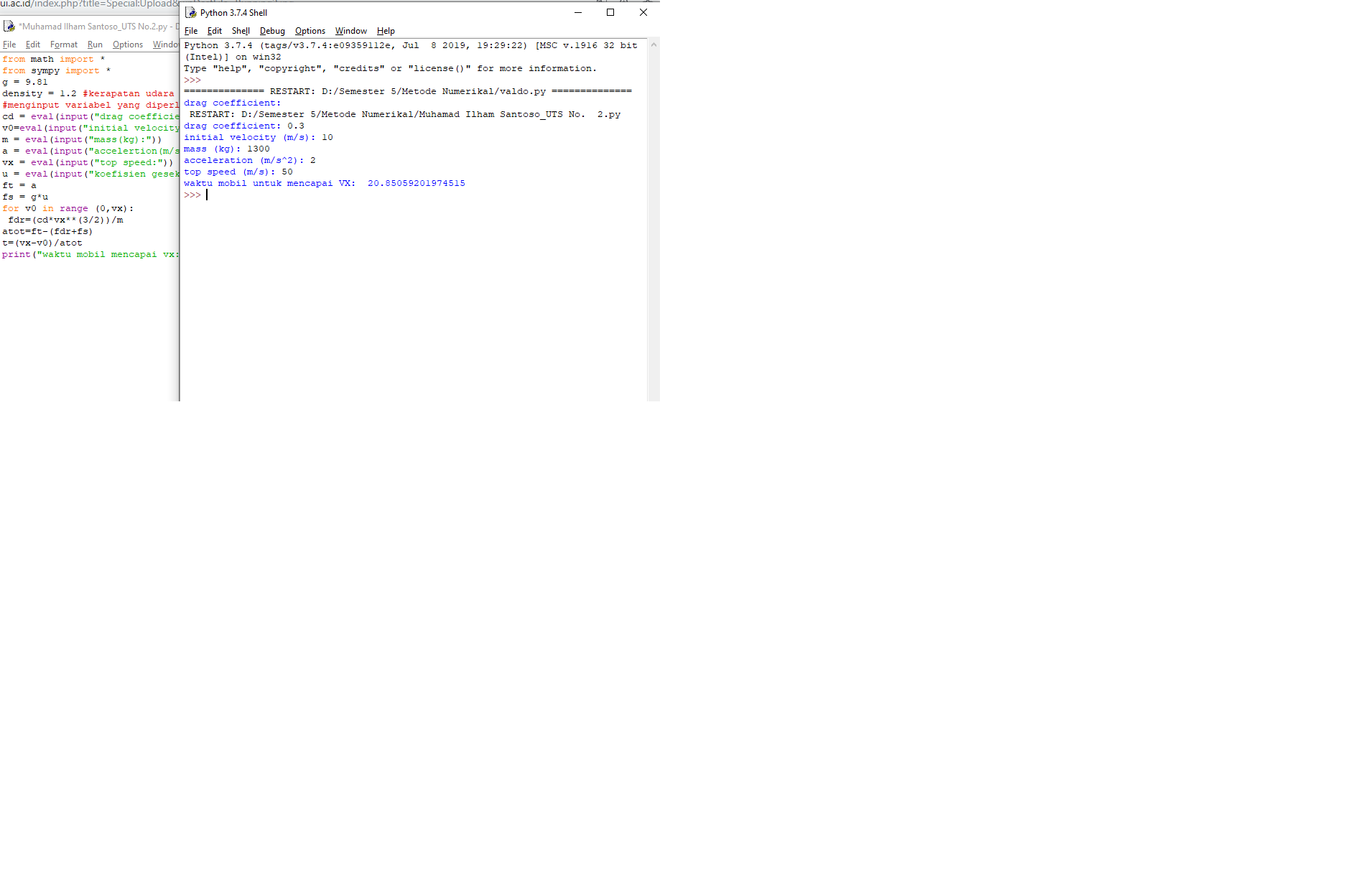
from math import *
from sympy import *
g = 9.81
density = 1.2 #kerapatan udara
#menginput variabel yang diperlukan
cd = eval(input("drag coefficient:"))
v0=eval(input("initial velocity (m/s): "))
area = eval(input("luas (m^2):"))
vx = eval(input("kecepatan maksimum:"))
m = eval(input("massa mobil(kg):"))
a = eval(input("accelertion(m/s^2)"))
u = eval(input("koefisien gesek:"))
ft = a
fs = g*u
for v0 in range (0,vx):
fdr=(cd*vx**(3/2))/m
atot=ft-(fdr+fs)
t=(vx-v0)/atot
print("waktu mobil mencapai vx:", t)
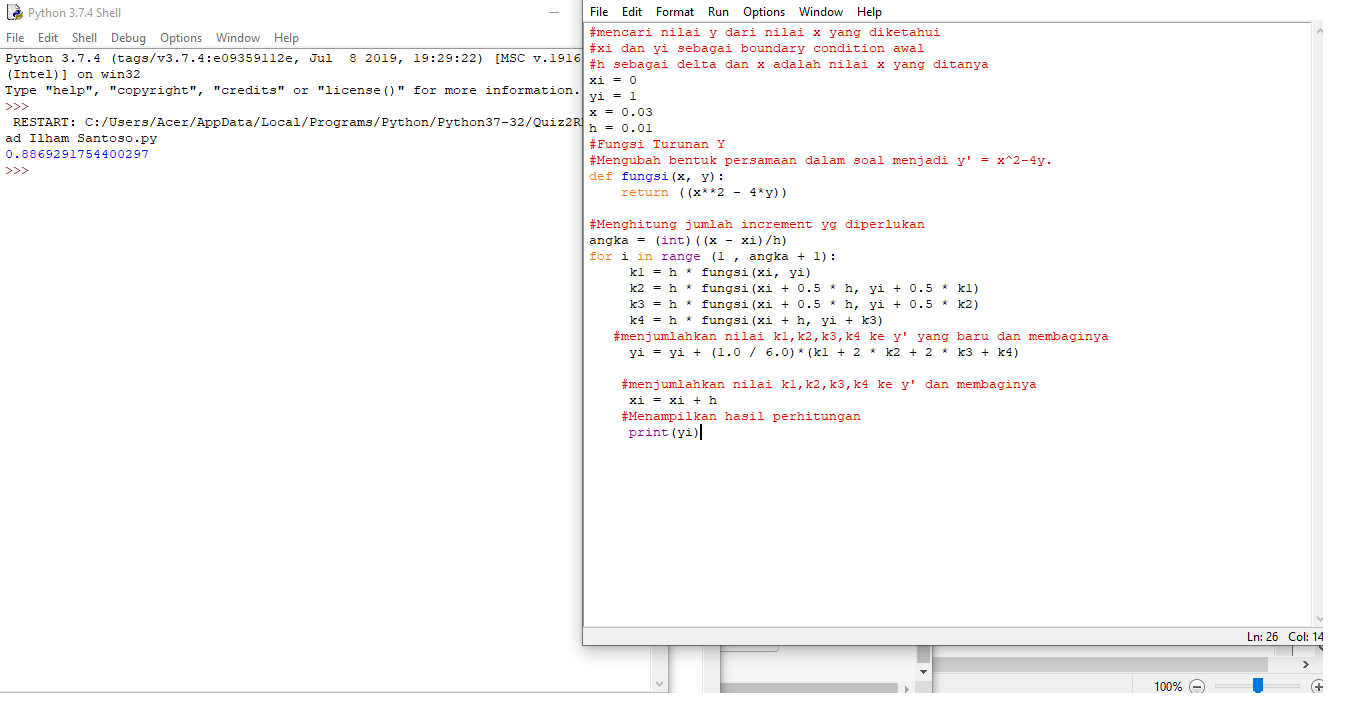
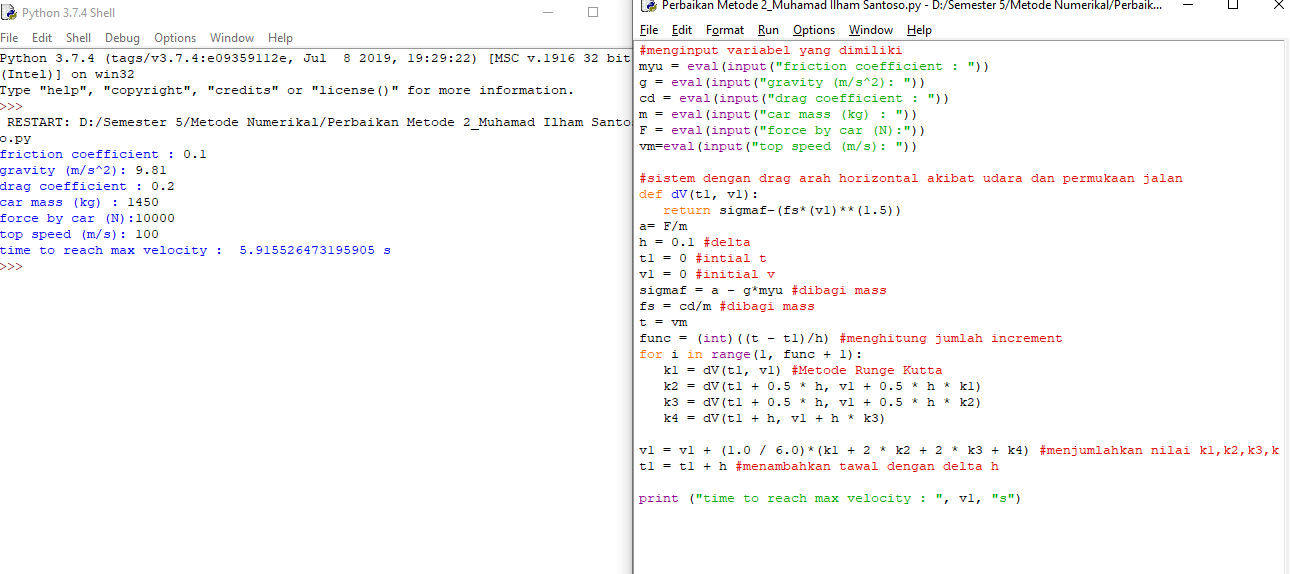
Cara 2 : Metode Runge Kutta
#menginput variabel yang dimiliki
myu = eval(input("friction coefficient : "))
g = eval(input("gravity (m/s^2): "))
cd = eval(input("drag coefficient : "))
m = eval(input("car mass (kg) : "))
F = eval(input("force by car (N):"))
vm=eval(input("top speed (m/s): "))
#sistem dengan drag arah horizontal akibat udara dan permukaan jalan def dV(t1, v1): return sigmaf-(fs*(v1)**(1.5)) a= F/m h = 0.1 #delta t1 = 0 #intial t v1 = 0 #initial v sigmaf = a - g*myu #dibagi mass fs = cd/m #dibagi mass t = vm func = (int)((t - t1)/h) #menghitung jumlah increment for i in range(1, func + 1): k1 = dV(t1, v1) #Metode Runge Kutta k2 = dV(t1 + 0.5 * h, v1 + 0.5 * h * k1) k3 = dV(t1 + 0.5 * h, v1 + 0.5 * h * k2) k4 = dV(t1 + h, v1 + h * k3) v1 = v1 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #menjumlahkan nilai k1,k2,k3,k4 ke z1 dan membaginya t1 = t1 + h #menambahkan tawal dengan delta h
print ("time to reach max velocity : ", v1, "s")
Video Muhasabah Diri
https://youtu.be/La4cpJBON6g (high resolution ver.1)
https://youtu.be/C20S86ex7ek (high resolution ver.2)
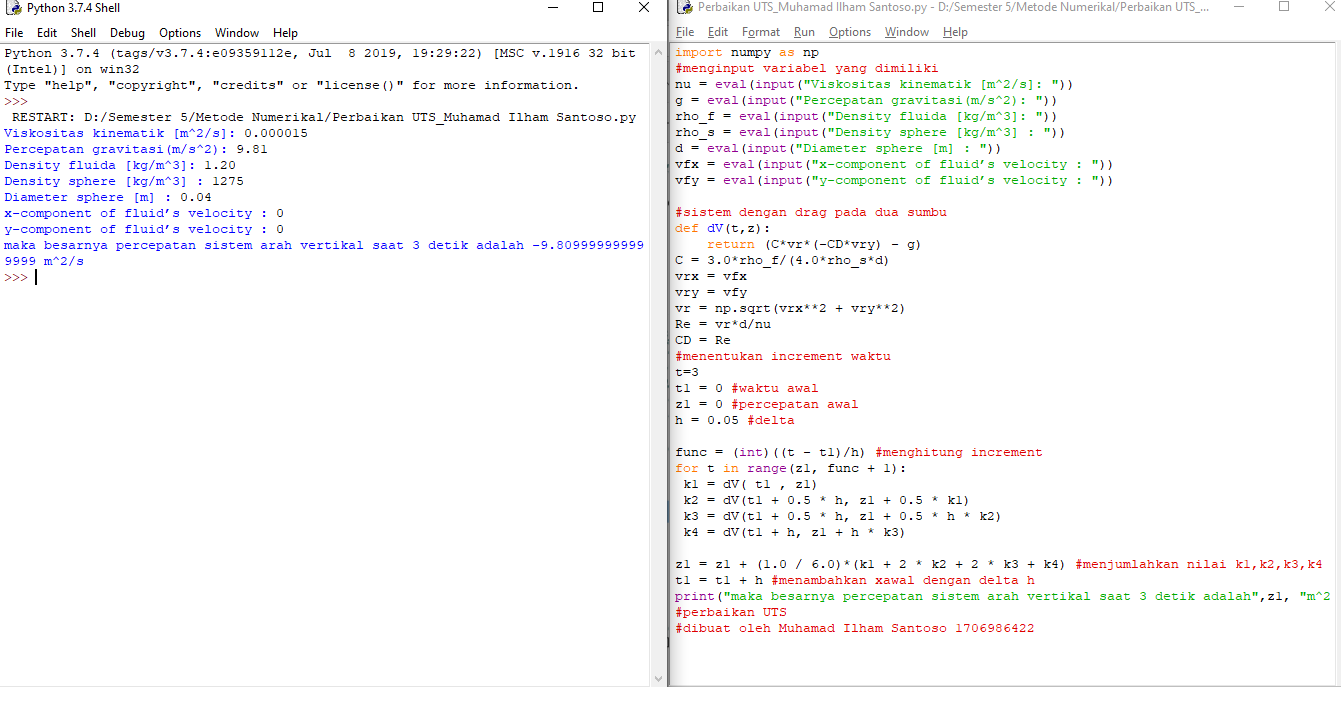
System for smooth sphere with drag in two directions (Runge Kutta Method)
import numpy as np
#menginput variabel yang dimiliki
nu = eval(input("Viskositas kinematik [m^2/s]: "))
g = eval(input("Percepatan gravitasi(m/s^2): "))
rho_f = eval(input("Density fluida [kg/m^3]: "))
rho_s = eval(input("Density sphere [kg/m^3] : "))
d = eval(input("Diameter sphere [m] : "))
vfx = eval(input("x-component of fluid’s velocity : "))
vfy = eval(input("y-component of fluid’s velocity : "))
#sistem dengan drag pada dua sumbu
def dV(t,z):
return (C*vr*(-CD*vry) - g)
C = 3.0*rho_f/(4.0*rho_s*d)
vrx = vfx
vry = vfy
vr = np.sqrt(vrx**2 + vry**2)
Re = vr*d/nu
CD = Re
#menentukan increment waktu
t=3
t1 = 0 #waktu awal
z1 = 0 #percepatan awal
h = 0.05 #delta
func = (int)((t - t1)/h) #menghitung increment
for t in range(z1, func + 1):
k1 = dV( t1 , z1)
k2 = dV(t1 + 0.5 * h, z1 + 0.5 * k1)
k3 = dV(t1 + 0.5 * h, z1 + 0.5 * h * k2)
k4 = dV(t1 + h, z1 + h * k3)
z1 = z1 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #menjumlahkan nilai k1,k2,k3,k4 ke z1 dan membaginya
t1 = t1 + h #menambahkan xawal dengan delta h
print("maka besarnya percepatan sistem arah vertikal saat 3 detik adalah",z1, "m^2/s")
#perbaikan UTS
#dibuat oleh Muhamad Ilham Santoso 1706986422


Enable comment auto-refresher
Auliarifai
Permalink |
Rizkiumas
Permalink |