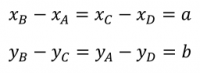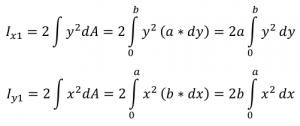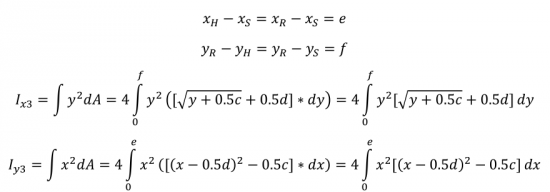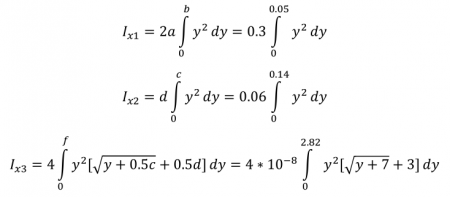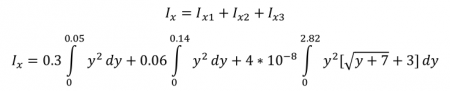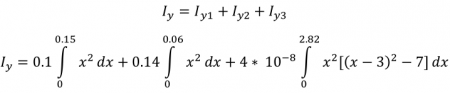Difference between revisions of "Tugas UTS Ismail"

From ccitonlinewiki
Jump to: navigation, search
(x)
(formatting)
 
(5 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
<div style="text-align: justify;">
 
<div style="text-align: justify;">
−
==Tugas UTS==
 
 
[[File:Acad_2019-04-01_21-58-28.png|center|300px]]
 
[[File:Acad_2019-04-01_21-58-28.png|center|300px]]
 
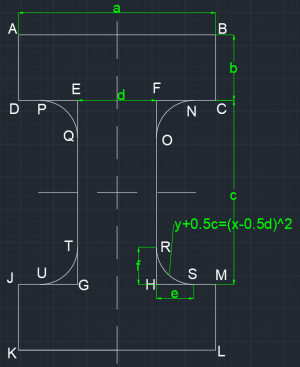
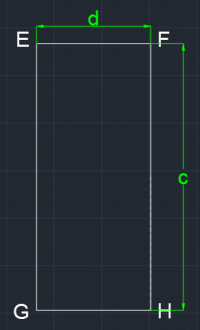
<div style="text-align: center;">Gambar 1. Penampang balok kolom pada bidang x-y</div>
 
<div style="text-align: center;">Gambar 1. Penampang balok kolom pada bidang x-y</div>
Line 31: Line 30:
 
Bagian 3 memiliki bentuk berupa fungsi f(x) = (x-0.5d)<sup>2</sup> - 0.5c dari titik x<sub>H</sub> ke x<sub>S</sub> dan y<sub>R</sub> ke y<sub>H</sub>. Selain balok HRS, balok yang juga merupakan bagian 3 adalah balok GTU, EPQ dan FNO. Perumusan untuk inersia ke arah x (I<sub>x</sub>) dan inersia ke arah y (I<sub>y</sub>) pada bagian 3 adalah:
 
Bagian 3 memiliki bentuk berupa fungsi f(x) = (x-0.5d)<sup>2</sup> - 0.5c dari titik x<sub>H</sub> ke x<sub>S</sub> dan y<sub>R</sub> ke y<sub>H</sub>. Selain balok HRS, balok yang juga merupakan bagian 3 adalah balok GTU, EPQ dan FNO. Perumusan untuk inersia ke arah x (I<sub>x</sub>) dan inersia ke arah y (I<sub>y</sub>) pada bagian 3 adalah:
  
−
[[File:SumatraPDF_2019-04-05_23-29-53.png|center|500px]]
+
[[File:SumatraPDF_2019-04-05_23-29-53.png|center|550px]]
−
</div>
 
 
----
 
----
 
===Total===
 
===Total===
 
----
 
----
 +
Setelah dicari inersia untuk tiap bagian, kemudian inersia dijumlah sehingga nilai I<sub>x</sub> dan I<sub>y</sub> untuk gambar 1 adalah:
 +
[[File:SumatraPDF_2019-04-05_23-32-00.png|center|150px]]
 +
----
 +
===Contoh Soal===
 +
----
 +
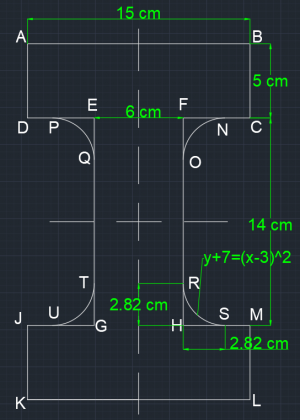
[[File:Acad_2019-04-01_22-18-10.png|center|300px]]
 +
<div style="text-align: center;">Gambar 5. Penampang balok kolom dengan ukuran bidang x-y</div>
 +
 +
Diketahui:
 +
* a = 15 cm = 0.15 m
 +
* b = 5 cm = 0.05 m
 +
* c = 14 cm = 0.14 m
 +
* d = 6 cm = 0.06 m
 +
* e = f = 2.82 cm = 0.0282 m
 +
* f(x)<sub>HRS, GTU, EPQ, FNO</sub>= (x – 3)<sup>2</sup> – 7
 +
 +
Ditanya: I<sub>x</sub> dan I<sub>y</sub> balok kolom?
 +
 +
Dijawab:
 +
 +
====Flowchart pengerjaan====
 +
[[File:SumatraPDF_2019-04-05_23-38-36.png|center|600px]]
 +
 +
====Inersia pada sumbu x====
 +
[[File:SumatraPDF_2019-04-05_23-40-20.png|center|450px]]
 +
Sehingga I<sub>x</sub> untuk balok kolom tersebut adalah
 +
[[File:SumatraPDF_2019-04-05_23-41-34.png|center|450px]]
 +
 +
====Inersia pada sumbu y====
 +
[[File:SumatraPDF_2019-04-05_23-42-57.png|center|450px]]
 +
Sehingga I x untuk balok tersebut adalah
 +
[[File:SumatraPDF_2019-04-05_23-43-57.png|center|450px]]
 +
 +
====Inersia pada sumbu y====
  
−
----
+
Setelah perumusan I<sub>x</sub> dan I<sub>y</sub> didapat, maka rumus-rumus yang telah dimodelkan akan diselesaikan dengan menggunakan software EES. Input yang dimasukkan adalah:
 +
 
 +
{definisi parameter}
 +
a = 0.15 "dalam meter"
 +
b = 0.05 "dalam meter"
 +
c = 0.14 "dalam meter"
 +
d = 0.06 "dalam meter"
 +
e = 2.82 "dalam centimeter"
 +
f = 2.82 "dalam centimeter"
 +
&nbsp;
 +
&nbsp;
 +
{mencari Ix}
 +
Ix1=integral(2*a*y1^2,y1,0,b)
 +
Ix2=integral(d*y2^2,y2,0,c)
 +
Ix3=integral(4*10^(-8)*(y3^2)*((y3+0.5*c)^0.5+0.5*d),y3,0,f)
 +
Ix=Ix1+Ix2+Ix3
 +
{selesai mencari Ix}
 +
&nbsp;
 +
&nbsp;
 +
{mencari Iy}
 +
Iy1=integral(2*b*x1^2,x1,0,a)
 +
Iy2=integral(c*x2^2,x2,0,d)
 +
Iy3=integral(4*10^(-8)*(x3^2)*((x3-0.5*d)^2-0.5*c),x3,0,e)
 +
Iy=Iy1+Iy2+Iy3
 +
{selesai mencari Iy}
 +
&nbsp;
 +
&nbsp;
 +
{
 +
CATATAN:
 +
Rumus integral => integral(fungsi, variable yang ingin diintegralkan, batas bawah, batas atas)
 +
Jadi, jika fungsi pada bagian 3 ingin dirubah, cukup hanya merubah "fungsi" pada Ix3 dan Iy3. Dalam hal ini, fungsi 3 hasilnya adalah cm^4 sehingga perlu diconvert ke m^4 dengan mengalikan 10^-8 pada persamaan.
 +
}
 +
 
 +
====Hasil====
 +
Dari hasil iterasi yang dilakukan EES, didapatkan hasil I<sub>x</sub> dan I<sub>y</sub> untuk balok kolom adalah
 +
 
 +
* I<sub>x</sub> = 6.783 x 10<sup>-5</sup> m<sup>4</sup>
 +
* I<sub>y</sub> = 1.239 x 10<sup>-4</sup> m<sup>4</sup>
 +
 
 +
dengan hasil inersia untuk masing-masing bagian adalah
 +
 
 +
Bagian 1:
 +
I<sub>x1</sub> = 1.25 x 10<sup>-5</sup> m<sup>4</sup>
 +
I<sub>y1</sub> = 1.125 x 10<sup>-4</sup> m<sup>4</sup>
 +
Bagian 2:
 +
I<sub>x2</sub> = 5.488 x 10<sup>-5</sup> m<sup>4</sup>
 +
I<sub>y2</sub> = 1.008 x 10<sup>-5</sup> m<sup>4</sup>
 +
Bagian 3:
 +
I<sub>x3</sub> = 4.468 x 10<sup>-7</sup> m<sup>4</sup>
 +
I<sub>y3</sub> = 1.368 x 10<sup>-6</sup> m<sup>4</sup>
 +
 
 +
[[File:EES_2019-04-02_09-03-33.png|center|500px]]
 +
<div style="text-align: center;">Gambar 6. Tampilan window EES yang menunjukan hasil iterasi</div>
 +
</div>

Latest revision as of 23:46, 6 April 2019

Acad 2019-04-01 21-58-28.png
Gambar 1. Penampang balok kolom pada bidang x-y

Akan dicari inersia ke arah x (I x ) dan inersia ke arah y (I y ) untuk sebuah permukaan benda di gambar 1. Untuk mencari inersia tersebut, benda dibagi menjadi beberapa bagian. Hal tersebut dikarenakan inersia bersifat skalar sehingga hasil dapat dihitung dengan artimatika biasa. Bagian-bagian yang dihitung adalah:

Bagian 1

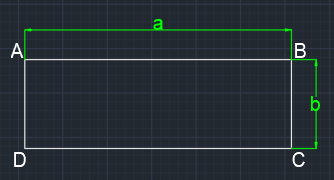
Acad 2019-04-01 18-11-31.png
Gambar 2. Penampang bagian 1 pada balok ABCD

Bagian 1 memiliki bentuk persegi panjang dengan luas a x b. Selain balok ABCD, balok yang juga merupakan bagian I adalah balok JKLM. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 1 adalah:

SumatraPDF 2019-04-05 23-20-42.png
SumatraPDF 2019-04-05 23-22-30.png

Bagian 2

Acad 2019-04-01 21-42-09.png
Gambar 3. Penampang bagian 2 pada balok EFGH

Bagian 2 memiliki bentuk persegi panjang dengan luas c x d. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 2 adalah:

SumatraPDF 2019-04-05 23-24-27.png

Bagian 3

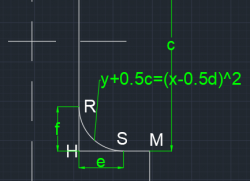
Acad 2019-04-01 22-00-04.png
Gambar 4. Penampang bagian 3 pada balok HRS

Bagian 3 memiliki bentuk berupa fungsi f(x) = (x-0.5d)2 - 0.5c dari titik xH ke xS dan yR ke yH. Selain balok HRS, balok yang juga merupakan bagian 3 adalah balok GTU, EPQ dan FNO. Perumusan untuk inersia ke arah x (Ix) dan inersia ke arah y (Iy) pada bagian 3 adalah:

SumatraPDF 2019-04-05 23-29-53.png

Total

Setelah dicari inersia untuk tiap bagian, kemudian inersia dijumlah sehingga nilai Ix dan Iy untuk gambar 1 adalah:

SumatraPDF 2019-04-05 23-32-00.png

Contoh Soal

Acad 2019-04-01 22-18-10.png
Gambar 5. Penampang balok kolom dengan ukuran bidang x-y

Diketahui:

  • a = 15 cm = 0.15 m
  • b = 5 cm = 0.05 m
  • c = 14 cm = 0.14 m
  • d = 6 cm = 0.06 m
  • e = f = 2.82 cm = 0.0282 m
  • f(x)HRS, GTU, EPQ, FNO= (x – 3)2 – 7

Ditanya: Ix dan Iy balok kolom?

Dijawab:

Flowchart pengerjaan

SumatraPDF 2019-04-05 23-38-36.png

Inersia pada sumbu x

SumatraPDF 2019-04-05 23-40-20.png

Sehingga Ix untuk balok kolom tersebut adalah

SumatraPDF 2019-04-05 23-41-34.png

Inersia pada sumbu y

SumatraPDF 2019-04-05 23-42-57.png

Sehingga I x untuk balok tersebut adalah

SumatraPDF 2019-04-05 23-43-57.png

Inersia pada sumbu y

Setelah perumusan Ix dan Iy didapat, maka rumus-rumus yang telah dimodelkan akan diselesaikan dengan menggunakan software EES. Input yang dimasukkan adalah: 

{definisi parameter}
a = 0.15 "dalam meter"
b = 0.05 "dalam meter"
c = 0.14 "dalam meter"
d = 0.06 "dalam meter"
e = 2.82 "dalam centimeter"
f = 2.82 "dalam centimeter"
 
 
{mencari Ix}
Ix1=integral(2*a*y1^2,y1,0,b)
Ix2=integral(d*y2^2,y2,0,c)
Ix3=integral(4*10^(-8)*(y3^2)*((y3+0.5*c)^0.5+0.5*d),y3,0,f)
Ix=Ix1+Ix2+Ix3
{selesai mencari Ix}
 
 
{mencari Iy}
Iy1=integral(2*b*x1^2,x1,0,a)
Iy2=integral(c*x2^2,x2,0,d)
Iy3=integral(4*10^(-8)*(x3^2)*((x3-0.5*d)^2-0.5*c),x3,0,e)
Iy=Iy1+Iy2+Iy3
{selesai mencari Iy}
 
 
{
CATATAN:
Rumus integral => integral(fungsi, variable yang ingin diintegralkan, batas bawah, batas atas)
Jadi, jika fungsi pada bagian 3 ingin dirubah, cukup hanya merubah "fungsi" pada Ix3 dan Iy3. Dalam hal ini, fungsi 3 hasilnya adalah cm^4 sehingga perlu diconvert ke m^4 dengan mengalikan 10^-8 pada persamaan.
}

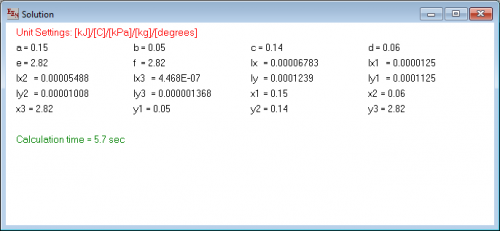
Hasil

Dari hasil iterasi yang dilakukan EES, didapatkan hasil Ix dan Iy untuk balok kolom adalah

  • Ix = 6.783 x 10-5 m4
  • Iy = 1.239 x 10-4 m4

dengan hasil inersia untuk masing-masing bagian adalah

Bagian 1: 

Ix1 = 1.25 x 10-5 m4
Iy1 = 1.125 x 10-4 m4

Bagian 2: 

Ix2 = 5.488 x 10-5 m4
Iy2 = 1.008 x 10-5 m4

Bagian 3: 

Ix3 = 4.468 x 10-7 m4
Iy3 = 1.368 x 10-6 m4
EES 2019-04-02 09-03-33.png
Gambar 6. Tampilan window EES yang menunjukan hasil iterasi
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Tugas_UTS_Ismail&oldid=5978"