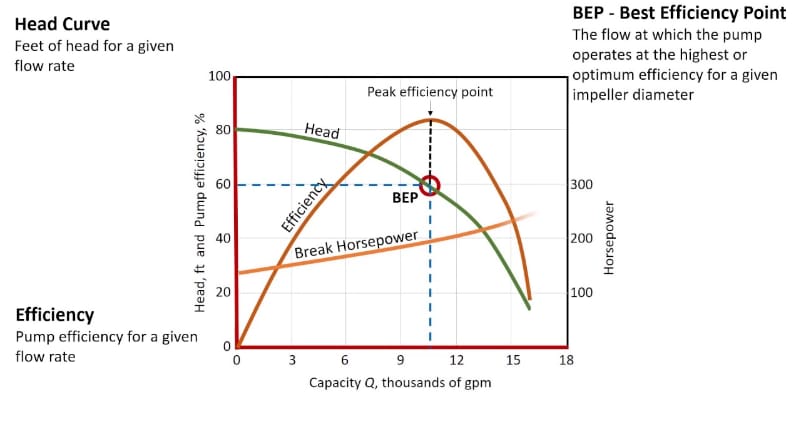
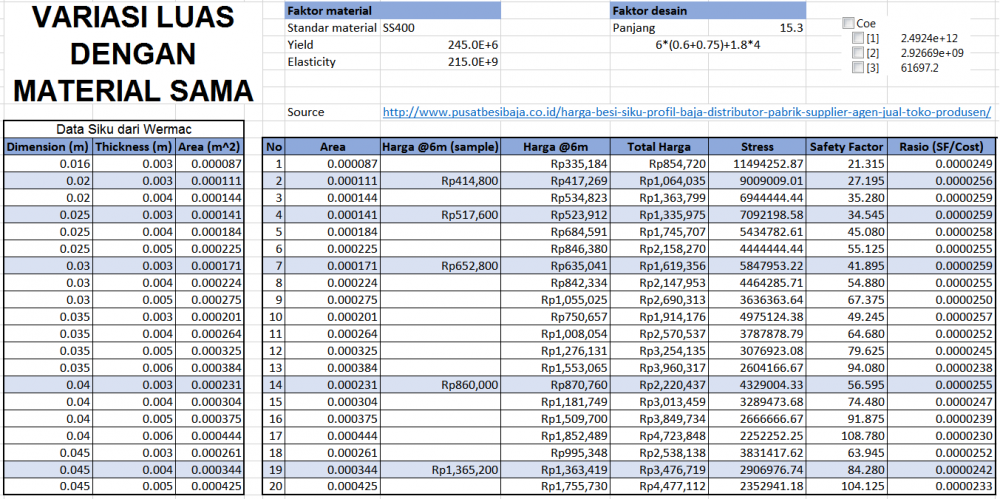
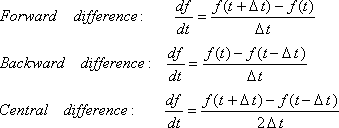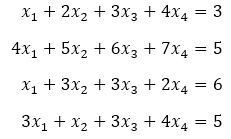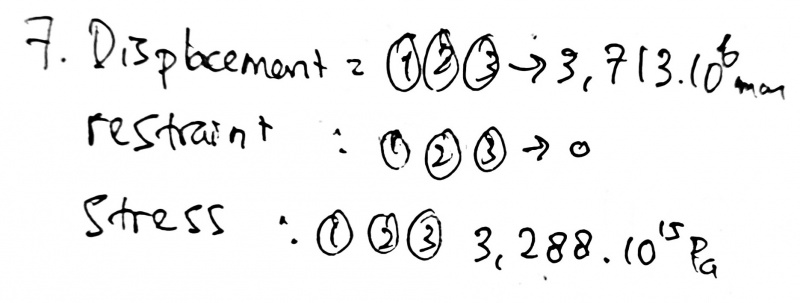Difference between revisions of "Metnum03-Hans Thiery T"
Hans.thiery (talk | contribs) |
Hans.thiery (talk | contribs) (→Ujian Akhir Semester (14 Januari 2021)) |
||
| (55 intermediate revisions by the same user not shown) | |||
| Line 17: | Line 17: | ||
ii. Metode bisection : metode incremental search method dengan mempersempit daerah pencarian akar-akar melalui batas atas dan batas bawah. | ii. Metode bisection : metode incremental search method dengan mempersempit daerah pencarian akar-akar melalui batas atas dan batas bawah. | ||
| − | iii. Metode posisi salah (False-Position) : mirip dengan metode Bisection, kecuali dalam penentuan titik tengah dari batas-batas yang telah ditentukan dengan persamaan | + | iii. Metode posisi salah (False-Position) : mirip dengan metode Bisection, kecuali dalam penentuan titik tengah dari batas-batas yang telah ditentukan dengan persamaan. |
| − | |||
b. Metode Open Methods merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method | b. Metode Open Methods merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method | ||
| Line 24: | Line 23: | ||
i. Metode Iterasi Sederhana (Fixed-Point Iteration) : memisahkan x dengan sebagian x yang lain sehingga diperoleh: x=g(x) | i. Metode Iterasi Sederhana (Fixed-Point Iteration) : memisahkan x dengan sebagian x yang lain sehingga diperoleh: x=g(x) | ||
| − | ii. Metode Newton-Raphson : menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut. | + | ii. Metode Newton-Raphson : menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut. |
| − | + | ||
| − | iii. Metode Secant : modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan). | + | iii. Metode Secant : modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan). |
| − | + | ||
| + | Rangkuman rumus / persamaannya : | ||
| + | |||
| + | [[File:Hans_Metnum_PraUTS1.png]] | ||
2.Regresi Linier | 2.Regresi Linier | ||
| Line 33: | Line 35: | ||
Persamaan umum Regresi Linier adalah sebagai berikut: | Persamaan umum Regresi Linier adalah sebagai berikut: | ||
| − | [[File: | + | [[File:Hans_Metnum_PraUTS2.png]] |
3. Turunan Numerik | 3. Turunan Numerik | ||
Turunan Numerik : penentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel, yang disajikan dalam 3 pendekatan sebagai berikut | Turunan Numerik : penentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel, yang disajikan dalam 3 pendekatan sebagai berikut | ||
| − | [[File: | + | [[File:Hans_Metnum_PraUTS3.png]] |
==Pertemuan 01 (Senin, 09 November 2020) : Pengenalan Aplikasi Open Modelica== | ==Pertemuan 01 (Senin, 09 November 2020) : Pengenalan Aplikasi Open Modelica== | ||
| Line 156: | Line 158: | ||
Dapat dikerjakan dengan flowchart : | Dapat dikerjakan dengan flowchart : | ||
| + | |||
[[File:Hans_Metnum_Kuis1_FlowChart4.jpg | 800x800px]] | [[File:Hans_Metnum_Kuis1_FlowChart4.jpg | 800x800px]] | ||
Dari flowchart tersebut, dapat diaplikasikan pada coding sebagai berikut | Dari flowchart tersebut, dapat diaplikasikan pada coding sebagai berikut | ||
| − | - Fungsi Utama | + | - '''Fungsi Utama''' |
class QuizSoal1 | class QuizSoal1 | ||
| − | + | parameter Real [:,7] inisiasi = [1, 1, 2, 0, 10e-4, 200e9, 1.00; | |
| − | + | 2, 2, 3, 0, 10e-4, 200e9, 1.00; | |
| − | + | 3, 1, 4, 308.66, 10e-4, 200e9, 1.60; | |
| − | + | 4, 2, 4, 270.00, 10e-4, 200e9, 1.25; | |
| − | + | 5, 3, 4, 231.34, 10e-4, 200e9, 1.60]; | |
| − | + | parameter Integer [:,2] node = [1, 2; | |
| − | + | 2, 3; | |
| − | + | 1, 4; | |
| − | + | 2, 4; | |
| − | + | 3, 4]; | |
| − | + | parameter Integer y = size(node,1); | |
| − | + | parameter Integer x = 2*(size(node_load,1)); | |
| − | + | parameter Integer z = size(Boundary,1); | |
| − | + | parameter Integer [:] Boundary = {1,3}; | |
| − | + | parameter Real [:,3] node_load = [1, 0, 0; | |
| − | + | 2, -1035.28, -3863.70; | |
| − | + | 3, 0, 0; | |
| − | + | 4, -1035.28, -3863.70]; | |
| − | + | parameter Real [2*(size(node_load,1))] load = {0,0,-1035.28,-3863.70,0,0,-1035.28,-3863.70}; | |
| − | + | Real [y] k; | |
| − | + | Real [y,4,4] Ke; | |
| − | + | Real [y,x,x] Kg; | |
| − | + | Real [x,x] KgTot; | |
| − | + | Real [x,x] KgB; | |
| − | + | Real [x] U; | |
| − | + | Real [x] R; | |
| − | + | equation | |
| − | + | k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)}; | |
| − | + | Ke = StiffnessMatrixElement(inisiasi); | |
| − | + | Kg = StiffnessMatrixGlobal(node, x, y, Ke); | |
| − | + | KgTot = SumStiffnessMatrixGlobal(x, y, Kg); | |
| − | + | KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); | |
| − | + | U = GaussJordan(x, KgB, load); | |
| − | + | R = ReactionForce(x, KgTot, U, load); | |
| − | + | F = CheckForce(load,R); | |
| − | + | end QuizSoal1; | |
| − | + | ||
| − | + | - '''Fungsi Matriks Elemen (Stiffness Matrix Element)''' | |
| − | + | function StiffnessMatrixElement | |
| − | + | input Real [:,7] inisiasi_mat; | |
| − | + | output Real [size(inisiasi_mat,1),4,4] Ke_mat; | |
| − | + | protected | |
| − | end | + | Real theta; |
| + | Real [3] StiffTrig; | ||
| + | Real [4,4] StiffTrans; | ||
| + | Real [size(inisiasi_mat,1)] k_vec; | ||
| + | Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / inisiasi_mat[i,7]) for i in 1:size(inisiasi_mat,1)}; | ||
| + | for i in 1:size(inisiasi_mat,1) loop | ||
| + | StiffTrig := zeros(3); | ||
| + | StiffTrans := zeros(4,4); | ||
| + | theta := Modelica.SIunits.Conversions.from_deg(inisiasi_mat[i,4]); | ||
| + | // {cos^2, sin^2, sincos} | ||
| + | StiffTrig := {(Modelica.Math.cos(theta))^2, | ||
| + | (Modelica.Math.sin(theta))^2, | ||
| + | (Modelica.Math.sin(theta)*Modelica.Math.cos(theta))}; | ||
| + | for t in 1:size(StiffTrig,1) loop | ||
| + | if abs(StiffTrig[t]) <= float_error then | ||
| + | StiffTrig[t] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[3], -1*StiffTrig[1], -1*StiffTrig[3]; | ||
| + | StiffTrig[3], StiffTrig[2], -1*StiffTrig[3], -1*StiffTrig[2]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[3], StiffTrig[1], StiffTrig[3]; | ||
| + | -1*StiffTrig[3], -1*StiffTrig[2], StiffTrig[3], StiffTrig[2]]; | ||
| + | for m in 1:4 loop | ||
| + | for n in 1:4 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end StiffnessMatrixElement; | ||
| + | |||
| + | - '''Stiffness Matrix Global''' | ||
| + | function StiffnessMatrixGlobal | ||
| + | input Integer [:,2] n; | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,4,4] Ke_mat; | ||
| + | output Real [y,x,x] Kg_mat; | ||
| + | algorithm | ||
| + | for i in 1:y loop | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | Kg_mat[i,a,b]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | for i in 1:y loop | ||
| + | Kg_mat[i,2*n[i,1],2*n[i,1]]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,2*n[i,1]-1,2*n[i,1]-1]:=Ke_mat[i,1,1]; | ||
| + | Kg_mat[i,2*n[i,1],2*n[i,1]-1]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,2*n[i,1]-1,2*n[i,1]]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,2*n[i,2],2*n[i,2]]:=Ke_mat[i,4,4]; | ||
| + | Kg_mat[i,2*n[i,2]-1,2*n[i,2]-1]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,2*n[i,2],2*n[i,2]-1]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,2*n[i,2]-1,2*n[i,2]]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,2*n[i,2],2*n[i,1]]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,2*n[i,2]-1,2*n[i,1]-1]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,2*n[i,2],2*n[i,1]-1]:=Ke_mat[i,4,1]; | ||
| + | Kg_mat[i,2*n[i,2]-1,2*n[i,1]]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,2*n[i,1],2*n[i,2]]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,2*n[i,1]-1,2*n[i,2]-1]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,2*n[i,1],2*n[i,2]-1]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,2*n[i,1]-1,2*n[i,2]]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end StiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Sum of Stiffness Matrix Global''' | ||
| + | function SumStiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,x,x] Kg_mat; | ||
| + | output Real [x,x] KgTot_mat; | ||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | end SumStiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Implement Boundary Condition''' | ||
| + | function BoundaryStiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer z; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Integer[z] Boundary_met; | ||
| + | output Real [x,x] KgB_met; | ||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgB_met[a,b] := KgTot_met [a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | for i in 1:x loop | ||
| + | for a in 1:z loop | ||
| + | for b in 0:1 loop | ||
| + | KgB_met[2*(Boundary_met[a])-b,i]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | for a in 1:z loop | ||
| + | for b in 0:1 loop | ||
| + | KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end BoundaryStiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Gauss-Jordan''' | ||
| + | function GaussJordan | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgB_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] U_met; | ||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | for i in 1:x loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end GaussJordan; | ||
| + | |||
| + | - '''Reaction Force''' | ||
| + | function ReactionForce | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Real [x] U_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] R_met; | ||
| + | algorithm | ||
| + | R_met := (KgTot_met*U_met)-load_met; | ||
| + | end ReactionForce; | ||
| − | + | Simulasi dilakukan hanya pada fungsi utama, hasilnya sebagai berikut | |
| + | [[File:Hans_Metnum_Kuis1_Hasil4.png]] | ||
Soal nomor 2 (8) : truss tiga dimensi | Soal nomor 2 (8) : truss tiga dimensi | ||
| + | |||
[[File:Hans_Metnum_Kuis1_Model8.png]] | [[File:Hans_Metnum_Kuis1_Model8.png]] | ||
Dapat dikerjakan dengan flowchart : | Dapat dikerjakan dengan flowchart : | ||
| + | |||
[[File:Hans_Metnum_Kuis1_FlowChart8.jpg | 800x800px]] | [[File:Hans_Metnum_Kuis1_FlowChart8.jpg | 800x800px]] | ||
Dari flowchart tersebut, dapat diaplikasikan pada coding sebagai berikut | Dari flowchart tersebut, dapat diaplikasikan pada coding sebagai berikut | ||
| − | - | + | |
| + | - '''Fungsi Utama''' | ||
| + | class QuizSoal2 | ||
| + | parameter Real [:,7] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5; | ||
| + | 2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5; | ||
| + | 3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5]; | ||
| + | parameter Integer [:,2] node = [1, 2; | ||
| + | 1, 3; | ||
| + | 1, 4]; | ||
| + | parameter Integer y = size(node,1); | ||
| + | parameter Integer x = 3*(size(node_load,1)); | ||
| + | parameter Integer z = size(Boundary,1); | ||
| + | parameter Integer [:] Boundary = {2,3,4}; | ||
| + | parameter Real [:,4] node_load = [1, 0, -5000, 0; | ||
| + | 2, 0, 0, 0; | ||
| + | 3, 0, 0, 0; | ||
| + | 4, 0, 0, 0]; | ||
| + | parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}; | ||
| + | Real [y] k; | ||
| + | Real [y,6,6] Ke; | ||
| + | Real [y,x,x] Kg; | ||
| + | Real [x,x] KgTot; | ||
| + | Real [x,x] KgB; | ||
| + | Real [x] U; | ||
| + | Real [x] R; | ||
| + | equation | ||
| + | k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y}; | ||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | Kg = StiffnessMatrixGlobal(node, x, y, Ke); | ||
| + | KgTot = SumStiffnessMatrixGlobal(x, y, Kg); | ||
| + | KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); | ||
| + | U = GaussJordan(x, KgB, load); | ||
| + | R = ReactionForce(x, KgTot, U, load); | ||
| + | F = CheckForce(load,R); | ||
| + | end QuizSoal2; | ||
| + | |||
| + | - '''Fungsi Matriks Elemen (Stiffness Matrix Element)''' | ||
| + | function StiffnessMatrixElement2 | ||
| + | input Real [:,9] inisiasi_mat; | ||
| + | output Real [size(inisiasi_mat,1),6,6] Ke_mat; | ||
| + | protected | ||
| + | Real cos_x; | ||
| + | Real cos_y; | ||
| + | Real [6] StiffTrig; | ||
| + | Real [6,6] StiffTrans; | ||
| + | Real [size(inisiasi_mat,1)] k_vec; | ||
| + | algorithm | ||
| + | k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)}; | ||
| + | for i in 1:size(inisiasi_mat,1) loop | ||
| + | StiffTrig := zeros(6); | ||
| + | StiffTrans := zeros(6,6); | ||
| + | cos_x := inisiasi_mat[i,4]; | ||
| + | cos_y := inisiasi_mat[i,5]; | ||
| + | cos_z := inisiasi_mat[i,6]; | ||
| + | StiffTrig := {(cos_x)^2, | ||
| + | (cos_y)^2, | ||
| + | (cos_z)^2, | ||
| + | (cos_x*cos_y), | ||
| + | (cos_x*cos_z), | ||
| + | (cos_y*cos_z)}; | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5]; | ||
| + | StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6]; | ||
| + | StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5]; | ||
| + | -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6]; | ||
| + | -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]]; | ||
| + | for m in 1:6 loop | ||
| + | for n in 1:6 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end StiffnessMatrixElement2; | ||
| + | |||
| + | - '''Stiffness Matrix Global''' | ||
| + | function StiffnessMatrixGlobal2 | ||
| + | input Integer [:,2] n; | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,6,6] Ke_mat; | ||
| + | output Real [y,x,x] Kg_mat; | ||
| + | algorithm | ||
| + | for i in 1:y loop | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | Kg_mat[i,a,b]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | for i in 1:y loop | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end StiffnessMatrixGlobal2; | ||
| + | |||
| + | - '''Sum of Stiffness Matrix Global''' | ||
| + | function SumStiffnessMatrixGlobal2 | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,x,x] Kg_mat; | ||
| + | output Real [x,x] KgTot_mat; | ||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | end SumStiffnessMatrixGlobal2; | ||
| + | |||
| + | - '''Implement Boundary Condition''' | ||
| + | function BoundaryStiffnessMatrixGlobal2 | ||
| + | input Integer x; | ||
| + | input Integer z; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Integer[z] Boundary_met; | ||
| + | output Real [x,x] KgB_met; | ||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgB_met[a,b] := KgTot_met [a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | for i in 1:x loop | ||
| + | for a in 1:z loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*(Boundary_met[a])-b,i]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | for a in 1:z loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end BoundaryStiffnessMatrixGlobal2; | ||
| + | |||
| + | - '''Gauss-Jordan''' | ||
| + | function GaussJordan2 | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgB_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] U_met; | ||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | for i in 1:x loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end GaussJordan2; | ||
| + | |||
| + | - '''Reaction Force''' | ||
| + | function ReactionForce2 | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Real [x] U_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] R_met; | ||
| + | algorithm | ||
| + | R_met := (KgTot_met*U_met)-load_met; | ||
| + | end ReactionForce2; | ||
| + | |||
| + | Simulasi dilakukan hanya pada fungsi utama, hasilnya sebagai berikut | ||
| + | |||
| + | [[File:Hans_Metnum_Kuis1_Hasil8.png]] | ||
| + | |||
| + | ==Tugas 05 : Truss tiga dimensi== | ||
| + | |||
| + | [[File:Hans_Metnum_Tugas5_Model.jpg]] | ||
| + | |||
| + | Sesuai soal di atas, dapat diaplikasikan pada coding sebagai berikut | ||
| + | |||
| + | - '''Fungsi Utama''' | ||
| + | class Hans_Metnum_Tugas5_Main | ||
| + | parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data | ||
| + | 2, 0, 0, -6, 1.56, 10.6e6; | ||
| + | 3, 0, 6, -3, 1.56, 10.6e6; | ||
| + | 4, -6, 0, -3, 1.56, 10.6e6; | ||
| + | 5, -6, 6, 0, 1.56, 10.6e6; | ||
| + | 6, 0, 6, 3, 1.56, 10.6e6]; | ||
| + | parameter Integer [size(inisiasi,1),2] node = [1, 2; | ||
| + | 1, 3; | ||
| + | 1, 4; | ||
| + | 2, 3; | ||
| + | 2, 4; | ||
| + | 3, 4]; | ||
| + | |||
| + | parameter Integer n = 4; //isi sesuai data | ||
| + | parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data | ||
| + | parameter Integer [:] Boundary_xy = {4}; //isi sesuai data | ||
| + | parameter Integer [:] Boundary_xz = {0}; //isi sesuai data | ||
| + | parameter Integer [:] Boundary_yz = {0}; //isi sesuai data | ||
| + | parameter Integer [:] Boundary_x = {3}; //isi sesuai data | ||
| + | parameter Integer [:] Boundary_y = {0}; //isi sesuai data | ||
| + | parameter Integer [:] Boundary_z = {0}; //isi sesuai data | ||
| + | parameter Real [3*n] load = {0, 0, 0, //isi sesuai data | ||
| + | 0, -200, 0, | ||
| + | 0, 0, 0, | ||
| + | 0, 0, 0}; | ||
| + | Real [size(inisiasi,1)] L; | ||
| + | Real [size(inisiasi,1)] k; | ||
| + | Real [size(inisiasi,1),6,6] Ke; | ||
| + | Real [size(inisiasi,1),3*n,3*n] Kg; | ||
| + | Real [3*n,3*n] KgTot; | ||
| + | Real [3*n,3*n] KgB; | ||
| + | Real [3*n] U; | ||
| + | Real [3*n] R; | ||
| + | Real [3] F; | ||
| + | equation | ||
| + | L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)}; | ||
| + | k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)}; | ||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | Kg = StiffnessMatrixGlobal(n, node, Ke); | ||
| + | KgTot = SumStiffnessMatrixGlobal(Kg); | ||
| + | KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); | ||
| + | U = GaussJordan(KgB, load); | ||
| + | R = ReactionForce(KgTot, U, load); | ||
| + | F = CheckForce(load,R); | ||
| + | end Hans_Metnum_Tugas5_Main; | ||
| + | |||
| + | - '''Fungsi Matriks Elemen (Stiffness Matrix Element)''' | ||
| + | function Hans_Metnum_Tugas5_StiffnessMatrixElement | ||
| + | input Real [:,6] inisiasi_mat; | ||
| + | output Real [size(inisiasi_mat,1),6,6] Ke_mat; | ||
| + | protected | ||
| + | Real cos_x; | ||
| + | Real cos_y; | ||
| + | Real [6] StiffTrig; | ||
| + | Real [6,6] StiffTrans; | ||
| + | Real [size(inisiasi_mat,1)] k_vec; | ||
| + | algorithm | ||
| + | L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)}; | ||
| + | k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)}; | ||
| + | for i in 1:size(inisiasi_mat,1) loop | ||
| + | StiffTrig := zeros(6); | ||
| + | StiffTrans := zeros(6,6); | ||
| + | cos_x := inisiasi_mat[i,2]/L[i]; | ||
| + | cos_y := inisiasi_mat[i,3]/L[i]; | ||
| + | cos_z := inisiasi_mat[i,4]/L[i]; | ||
| + | StiffTrig := {(cos_x)^2, | ||
| + | (cos_y)^2, | ||
| + | (cos_z)^2, | ||
| + | (cos_x*cos_y), | ||
| + | (cos_x*cos_z), | ||
| + | (cos_y*cos_z)}; | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5]; | ||
| + | StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6]; | ||
| + | StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5]; | ||
| + | -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6]; | ||
| + | -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]]; | ||
| + | for m in 1:6 loop | ||
| + | for n in 1:6 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end Hans_Metnum_Tugas5_StiffnessMatrixElement; | ||
| + | |||
| + | - '''Stiffness Matrix Global''' | ||
| + | function Hans_Metnum_Tugas5_StiffnessMatrixGlobal | ||
| + | input Integer [:,2] n; | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,6,6] Ke_mat; | ||
| + | output Real [y,x,x] Kg_mat; | ||
| + | algorithm | ||
| + | Kg_mat:=zero(size(ke_mat,1),3*x,3*x); | ||
| + | for i in 1:size(Ke_mat,1) loop | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end Hans_Metnum_Tugas5_StiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Sum of Stiffness Matrix Global''' | ||
| + | function Hans_Metnum_Tugas5_SumStiffnessMatrixGlobal | ||
| + | input Real [:,:,:] Kg_mat; | ||
| + | output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat; | ||
| + | algorithm | ||
| + | for a in 1:size(Kg_mat,2) loop | ||
| + | for b in 1:size(Kg_mat,2) loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | end Hans_Metnum_Tugas5_SumStiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Implement Boundary Condition''' | ||
| + | function Hans_Metnum_Tugas5_BoundaryStiffnessMatrixGlobal | ||
| + | input Real [:,:] KgTot_met; | ||
| + | input Integer[:] Boundary_xyz; | ||
| + | input Integer[:] Boundary_xy; | ||
| + | input Integer[:] Boundary_xz; | ||
| + | input Integer[:] Boundary_yz; | ||
| + | input Integer[:] Boundary_x; | ||
| + | input Integer[:] Boundary_y; | ||
| + | input Integer[:] Boundary_z; | ||
| + | output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met; | ||
| + | algorithm | ||
| + | for a in 1:size(KgTot_met,1) loop | ||
| + | for b in 1:size(KgTot_met,1) loop | ||
| + | KgB_met[a,b] := KgTot_met [a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | if Boundary_xyz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xyz,1) loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*(Boundary_xyz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_xy[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xy,1) loop | ||
| + | for b in 1:2 loop | ||
| + | KgB_met[3*(Boundary_xy[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_xz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xz,1) loop | ||
| + | for b in 0:2:2 loop | ||
| + | KgB_met[3*(Boundary_xz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_yz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_yz,1) loop | ||
| + | for b in 0:1 loop | ||
| + | KgB_met[3*(Boundary_yz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_x[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_x,1) loop | ||
| + | KgB_met[3*(Boundary_x[a])-2,i]:=0; | ||
| + | KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_y[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_y,1) loop | ||
| + | KgB_met[3*(Boundary_y[a])-1,i]:=0; | ||
| + | KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_z[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_z,1) loop | ||
| + | KgB_met[3*Boundary_z[a],i]:=0; | ||
| + | KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | end Hans_Metnum_Tugas5_BoundaryStiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Gauss-Jordan''' | ||
| + | function Hans_Metnum_Tugas5_GaussJordan | ||
| + | input Real [:,:] KgB_met; | ||
| + | input Real [size(KgB_met,1)] load_met; | ||
| + | output Real [size(KgB_met,1)] U_met; | ||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | for i in 1:size(KgB_met,1) loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Hans_Metnum_Tugas5_GaussJordan; | ||
| + | |||
| + | - '''Reaction Force''' | ||
| + | function Hans_Metnum_Tugas5_ReactionForce | ||
| + | input Integer x; | ||
| + | input Real [:,:] KgTot_met; | ||
| + | input Real [size(KgTot_met,1)] U_met; | ||
| + | input Real [size(KgTot_met,1)] load_met; | ||
| + | output Real [x] R_met; | ||
| + | protected Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | R_met := (KgTot_met*U_met)-load_met; | ||
| + | for t in 1:size(KgTot_met,1) loop | ||
| + | if abs(R_met[t]) <= float_error then | ||
| + | R_met[t] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Hans_Metnum_Tugas5_ReactionForce; | ||
| + | |||
| + | - '''Pengecekan kesetimbangan gaya''' (resultan gaya = 0) | ||
| + | function Hans_Metnum_Tugas5_CheckForce | ||
| + | input Real [:] load; | ||
| + | input Real [size(load,1)] R; | ||
| + | output Real [3] F; | ||
| + | protected Real float_error = 10e-10; | ||
| + | protected | ||
| + | Real load_x; | ||
| + | Real load_y; | ||
| + | Real load_z; | ||
| + | Real R_x; | ||
| + | Real R_y; | ||
| + | Real R_z; | ||
| + | algorithm | ||
| + | load_x := sum({load[i] for i in 1:3:(size(load,1)-2)}); | ||
| + | load_y := sum({load[i] for i in 2:3:(size(load,1)-1)}); | ||
| + | load_z := sum({load[i] for i in 3:3:size(load,1)}); | ||
| + | R_x := sum({R[i] for i in 1:3:(size(load,1)-2)}); | ||
| + | R_y := sum({R[i] for i in 2:3:(size(load,1)-1)}); | ||
| + | R_z := sum({R[i] for i in 3:3:size(load,1)}); | ||
| + | F[1] := load_x + R_x; | ||
| + | F[2] := load_y + R_y; | ||
| + | F[3] := load_z + R_z; | ||
| + | for i in 1:3 loop | ||
| + | if abs(F[i]) <= float_error then | ||
| + | F[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Hans_Metnum_Tugas5_CheckForce; | ||
| + | |||
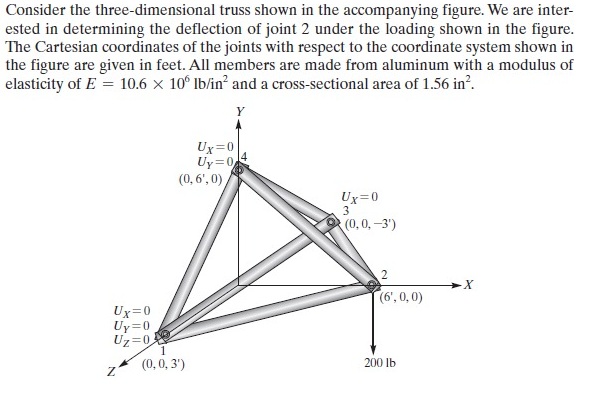
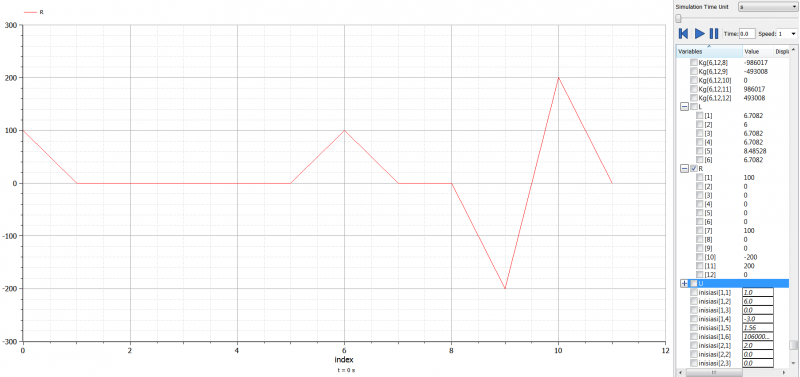
| + | Simulasi dilakukan hanya pada fungsi utama, hasilnya sebagai berikut | ||
| + | |||
| + | [[File:Hans_Metnum_Tugas5_ResultR.png | 800px]] | ||
| + | |||
| + | [[File:Hans_Metnum_Tugas5_ResultU.png | 800px]] | ||
| + | |||
| + | Didapatkan resultan gaya sama dengan nol | ||
| + | |||
| + | [[File:Hans_Metnum_Tugas5_ResultF.png | 800px]] | ||
| + | |||
| + | ==Pertemuan 06 (Senin, 14 Desember 2020) : Muhasabah Pemahaman Studi Kasus== | ||
| + | |||
| + | Pada perkuliahan ini, kami melakukan muhasabah diri sendiri terhadap pemahaman tentang metode numerik yang telah dipelajari pada semester ini, sebagai kesimpulan muhasabah saya adalah sebagai berikut | ||
| + | |||
| + | Pada pandangan saya, pemahaman saya mengenai dasar-dasar metode numerik sesuai pelajaran sebelum UTS sudah cukup baik untuk dilanjutkan pada tahapan selanjutnya, yaitu penerapan pada Open Modelica. Namun, selain pemahaman numerik, pemahaman mengenai dasar-dasar fisika, termasuk teori, hukum, dan fenomena haris dapat dipahami sebelum dilakukan aplikasi simulasi pada Open Modelica dengan membuat model matematika yang sesuai. Dengan Open Modelica dan aplikasi-aplikasi lainnya, kami dapat menyelesaikan permasalahan teknik secara mudah, tanpa perhitungan manual yang sangat panjang dan rawan terhadap kesilapan. Akan tetapi, bahasa pemograman Open Modelica yang cukup baru dan asing bagi saya, membuat saya harus mempelajarinya dari awal dan menyeluruh agar dapat menggunakannya secara maksimal dan efisien. Dengan pemahaman tersebut, saya dapat dengan mudah menyelesaikan berbagai masalah teknik, sesuai dengan prosedur atau flowchart penyelesaiannya. Saya berharap saya dapat memahaminya dengan baik, sehingga dapat mempraktikkannya ke depannya dan memenuhi kriteria kelulusan, serta menguasai ilmu yang diharapkan dimiliki oleh seorang mahasiswa teknik mesin. | ||
| + | |||
| + | ==Sinopsis Tugas Besar : Aplikasi Metoda Numerik dalam Optimasi Desain Struktur Rangka Sederhana== | ||
| + | |||
| + | Pada tugas besar Mata Kuliah Metode Numerik akan bertema optimasi desain struktur rangka. Aplikasi tersebut akan dilakukan dengan Open Modelica sesuai pemaparan / pembelajaran pada perkuliahan. Dengan pemograman tersebut, dapat dilakukan optimasi pada susunan desain rangka dengan pemograman yang efisien dan ringan. | ||
| + | |||
| + | ==Pertemuan 07 (Senin, 21 Desember 2020) : Aplikasi Metode Numerik dalam Kasus Optimasi== | ||
| + | |||
| + | Pada perkuliahan ini, Kami mendapatkan pemaparan mengenai topik Aplikasi Metode Numerik dalam Optimasi Desain Struktur Rangka Sederhana yang akan menjadi topik tugas besar. Secara garis besar, tujuan yang hendak dicapai adalah untuk menentukan material yang optimal dan murah untuk rangka sederhana (Truss). | ||
| + | |||
| + | [[File:Hans_Metnum_P7A1.jpg]] | ||
| + | |||
| + | Setelah itu Ibu Candra memberikan tutorial optimasi ''Bracket Optimization Using Golden Ratio'', yaitu dengan fungsi yang memiliki fungsi maksimum dan minimum lokal dan global. Sebagai contoh, kami melakukan optimasi pada soal : ''Tentukan nilai f(x) maksimum dengan metode golden ration dari fungsi f(x) = 2sinx-x^2/10'' | ||
| + | |||
| + | Dengan contoh tersebut dapat dilakukan coding sebagai berikut | ||
| + | |||
| + | model Hans_Metnum_bracket_optimation | ||
| + | parameter Integer n=8; | ||
| + | Real x1 [n]; | ||
| + | Real x2 [n]; | ||
| + | Real xup; | ||
| + | Real xlow; | ||
| + | Real d; | ||
| + | Real f1 [n]; | ||
| + | Real f2 [n]; | ||
| + | Real xopt; | ||
| + | Real yopt; | ||
| + | algorithm | ||
| + | xup :=4; | ||
| + | xlow :=0; | ||
| + | for i in (1:n) loop | ||
| + | d:=(5^(1/2)-1)/2*(xup-xlow); | ||
| + | x1[i] := xlow+d; | ||
| + | x2[i] := xup-d; | ||
| + | f1[i] := f_obj3(x1[i]); | ||
| + | f2[i] := f_obj3(x2[i]); | ||
| + | if f1[i]>f2[i] then | ||
| + | xup := xup; | ||
| + | xlow:= x2[i]; | ||
| + | xopt:= xup; | ||
| + | yopt:= f1[i]; | ||
| + | else | ||
| + | xlow := xlow; | ||
| + | xup := x1[i]; | ||
| + | xopt := xup; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Hans_Metnum_bracket_optimation; | ||
| + | |||
| + | dengan fungsi panggil: | ||
| + | |||
| + | function f_obj3 | ||
| + | import Modelica.Math; | ||
| + | input Real x; | ||
| + | output Real y; | ||
| + | algorithm | ||
| + | y:=2*Math.sin(x)-x^2/10; | ||
| + | end f_obj3; | ||
| + | |||
| + | Dari pengkodingan tersebut akan didapatkan f(x) maksimum yang secara konsep mirip dengan apa yang akan dilakukan pada tugas besar. | ||
| + | |||
| + | ==Pertemuan 08 (Senin, 28 Desember 2020) : Latihan Kasus Optimasi dengan Powell's Method== | ||
| + | |||
| + | [[File:Hans_Metnum_P8A1.jpg]] | ||
| + | |||
| + | [[File:Hans_Metnum_P8A2.jpg]] | ||
| + | |||
| + | [[File:Hans_Metnum_P8A3.jpg]] | ||
| + | |||
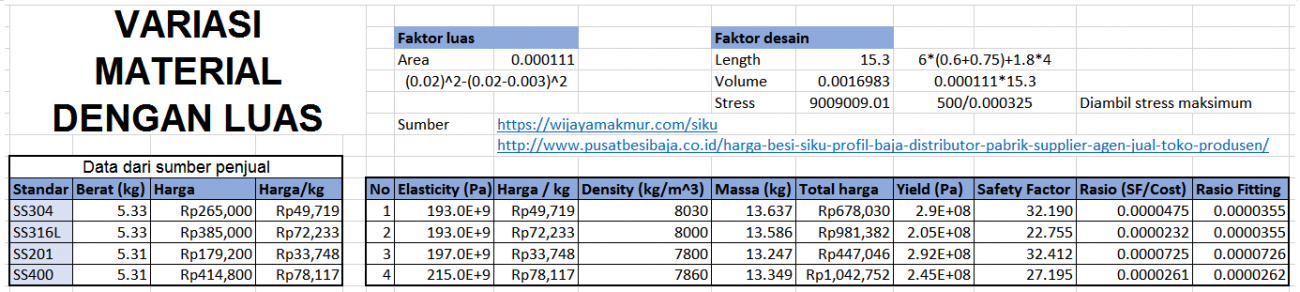
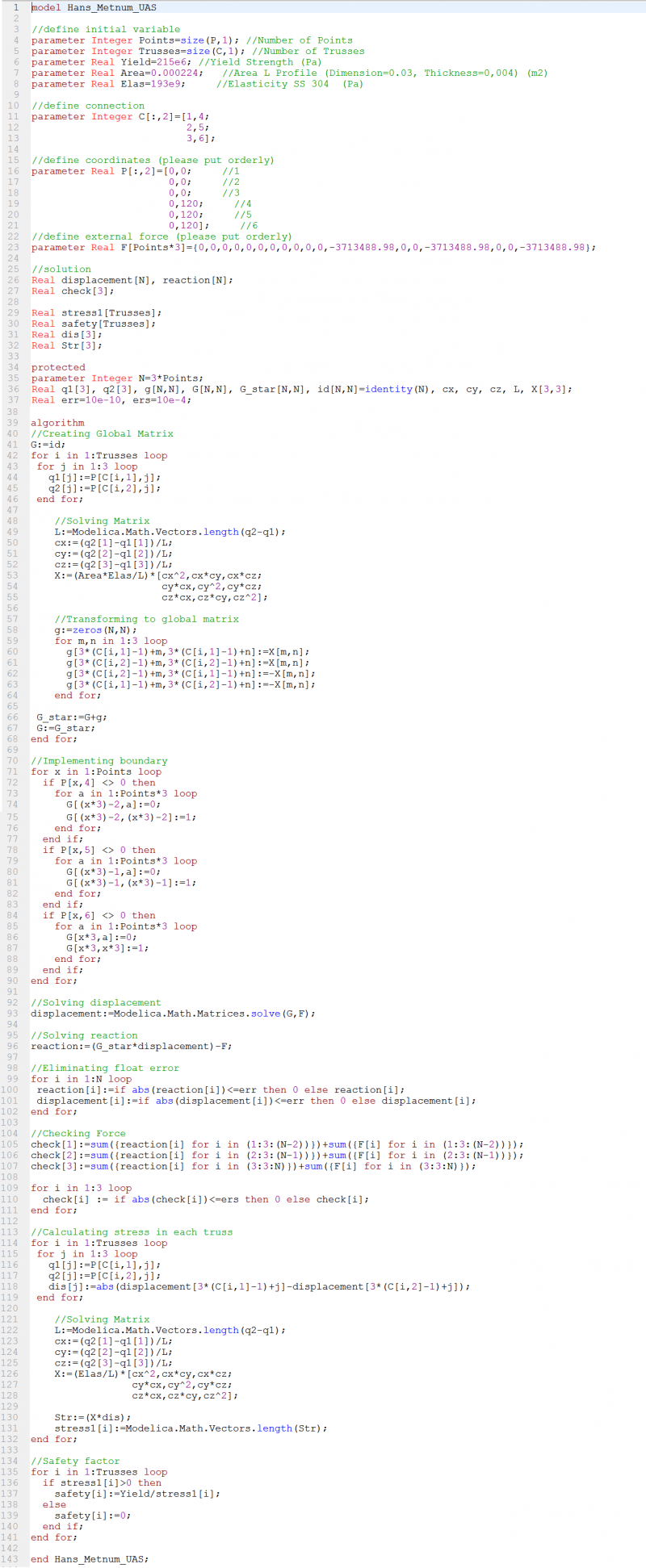
| + | ==Tugas Besar Metode Numerik : Optimasi Desain Struktur Rangka (Truss) Sedarhana dengan Open Modelica== | ||
| + | |||
| + | '''Latar Belakang''' | ||
| + | |||
| + | Optimasi pada suatu desain sangat diperlukan agar dapat menghasilkan desain yang paling optimal, sehingga didapatkan harga yang paling murah dengan kualitas mumpuni atau sesuai dengan spesifikasi target pemakaian | ||
| + | |||
| + | |||
| + | '''Tujuan''' | ||
| + | |||
| + | Mendapatkan desain dengan harga paling murah dan spesifikasi atau kemampuan mumpuni untuk target penggunaan (Spesifikasi material, luas, dan harga yang optimal) | ||
| + | |||
| + | |||
| + | '''Ilustrasi Model''' | ||
| + | |||
| + | [[File:Hans_Metnum_TubesModel.jpg]] | ||
| + | |||
| + | |||
| + | '''Data yang Diketahui''' | ||
| + | |||
| + | Jenis model : Rangka batang (bar element) dengan struktur batang | ||
| + | |||
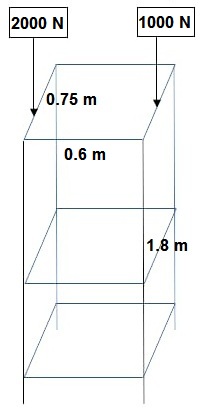
| + | Dimensi Rangka Batang : 0.6m x 0.75m x 1.8m (p x l x t) | ||
| + | |||
| + | F1 = 2000 N | ||
| + | |||
| + | F2 = 1000 N | ||
| + | |||
| + | |||
| + | '''Ketentuan''' | ||
| + | |||
| + | - Optimasi secara harga temurah dengan faktor berubah kekuatan dan area | ||
| + | |||
| + | - Tujuan optimasi : Displacement U minimum (kuat), Cross-area minimum, dan Nilai E dan A (murah) | ||
| + | |||
| + | |||
| + | '''Asumsi''' | ||
| + | |||
| + | - Lantai dasar fix | ||
| + | |||
| + | - Tidak ada bending | ||
| + | |||
| + | - Beban terdistribusi, sehingga dibagi dua pada setiap sudut | ||
| + | |||
| + | |||
| + | '''Metodologi''' | ||
| + | |||
| + | Dalam pengerjaan tugas besar ini, akan dibuat pencodingan sesuai model yang diberikan dengan tujuan optimasi mencari material dan ukuran yang paling cocok | ||
| + | |||
| + | |||
| + | '''Prosedur''' | ||
| + | |||
| + | 1. Menentukan Jarak Node dengan asumsi sendiri | ||
| + | |||
| + | 2. Menentukan Batasan Displacement dengan asumsi sendiri | ||
| + | |||
| + | 3. Mengoptimisasi E (elastisitas material), A (luas), dan harga sesuai standar / referensi dari produsen dilakukan dengan 2 fase, yaitu | ||
| + | a. Material bervariasi, area tetap untuk mencari material optimum | ||
| + | b. Material tetap, luas bervariasi untuk mencari dimensi atau ukuran optimum | ||
| + | menggunakan cara Curve Fitting dan Golden Section | ||
| + | |||
| + | 4. Memilih E/A untuk jadi patokan minimum dengan harga keseluruhan termurah (optimal) | ||
| + | |||
| + | |||
| + | '''Perencanaan Waktu''' | ||
| + | |||
| + | Ditargetkan untuk selesai sebelum tanggal pengumpulan terakhir | ||
| + | |||
| + | |||
| + | '''Koding''' | ||
| + | |||
| + | ''Trusses Modelling'' | ||
| + | |||
| + | model Hans_Metnum_TubesMain | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=''nilai yield strength''; //Yield Strength (Pa) | ||
| + | parameter Real Area=''nilai luas';; //Area L Profile | ||
| + | parameter Real Elas=''nilai elastisitas''; //Elasticity (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Hans_Metnum_TubesMain; | ||
| + | |||
| + | |||
| + | ''Curve Fitting'' | ||
| + | |||
| + | class Curvefitting | ||
| + | |||
| + | parameter Real X[''jumlah plot'']={''plot''}; | ||
| + | parameter Real Y[''jumlah plot'']={''plot''}; | ||
| + | Real Coe[3]; | ||
| + | |||
| + | algorithm | ||
| + | Coe:=Curve_Fitting(X,Y,2); | ||
| + | |||
| + | end Curvefitting; | ||
| + | |||
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | |||
| + | ''Golden Section'' | ||
| + | |||
| + | model Opt_Gold | ||
| + | |||
| + | parameter Real xd[:]; | ||
| + | parameter Real yd[size(xd,1)]; | ||
| + | parameter Real xlo=87e-6; | ||
| + | parameter Real xhi=504e-6; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Opt_Gold; | ||
| + | |||
| + | '''Hasil''' | ||
| + | |||
| + | [[File:Hans_Metnum_TubesA1b.png | 1000px]] | ||
| + | |||
| + | [[File:Hans_Metnum_TubesA2.png]] | ||
| + | |||
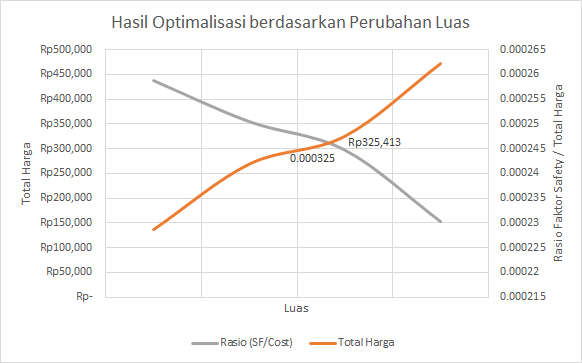
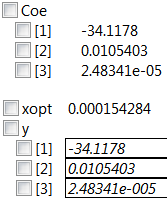
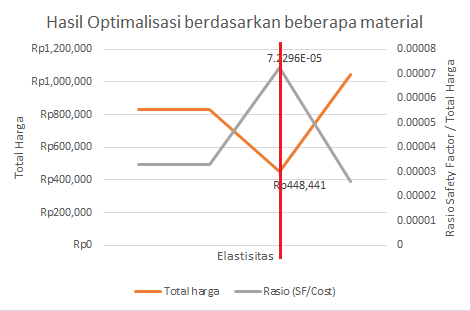
| + | Dengan optimasi, didapatkan : | ||
| + | |||
| + | [[File:Hans_Metnum_TubesA3.png]] | ||
| + | |||
| + | Kesimpulan : Luas optimal yang didapatkan adalah 0.00154 m^2 | ||
| + | |||
| + | |||
| + | [[File:Hans_Metnum_TubesB1b.png | 1300px]] | ||
| + | |||
| + | [[File:Hans_Metnum_TubesB2.png]] | ||
| + | |||
| + | Dengan optimasi, didapatkan : | ||
| + | |||
| + | [[File:Hans_Metnum_TubesB3.png]] | ||
| + | |||
| + | Kesimpulan : Elastisitas optimal yang didapatkan adalah 203 GPa | ||
| + | |||
| + | ==Ujian Akhir Semester (14 Januari 2021)== | ||
| + | |||
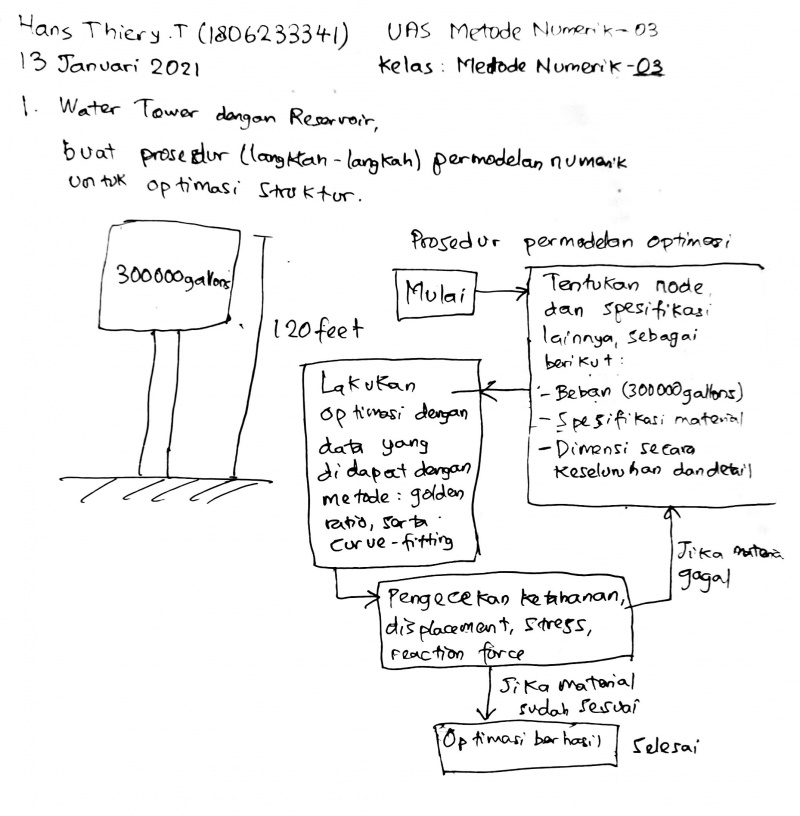
| + | Berikut adalah jawaban Ujian Akhir Semester Mata Kuliah Metode Numerik 03 saya | ||
| + | |||
| + | [[File:Hans_Metnum_UAS1.jpg | 800px]] | ||
| + | |||
| + | [[File:Hans_Metnum_UAS2.jpg | 800px]] | ||
| + | |||
| + | [[File:Hans_Metnum_UAS3.jpg | 800px]] | ||
| + | |||
| + | [[File:Hans_Metnum_UAS4&5.jpg | 800px]] | ||
| + | |||
| + | [[File:Hans_Metnum_UAS6.jpg | 800px]] | ||
| + | |||
| + | [[File:Hans_Metnum_UAS7a.jpg | 800px]] | ||
| − | + | [[File:Hans_Metnum_UAS7b.png | 800px]] | |
Latest revision as of 21:10, 14 January 2021
Nama : Hans Thiery T
NPM : 1806233341
Mata Kuliah : Metode Numerik 03 (TA 2020/2021 Ganjil)
Contents
- 1 Materi sebelum UTS
- 2 Pertemuan 01 (Senin, 09 November 2020) : Pengenalan Aplikasi Open Modelica
- 3 Tugas 01 : Pelajari dan memberikan satu contoh aplikasi pada Open Modelica
- 4 Pertemuan 02 (Senin, 16 November 2020) : Aplikasi mencari rata-rata dengan Open Modelica
- 5 Tugas 02 : Aplikasi Eliminasi Gauss untuk menyelesaikan persamaan-persamaan dengan Open Modelica
- 6 Pertemuan 03 (Senin, 23 November 2020) :
- 7 Tugas 03 : Aplikasi analisis pada Open Modelica
- 8 Pertemuan 04 (Senin, 30 November 2020)
- 9 Pertemuan 05 (Senin, 07 Desember 2020) : Pembahasan Kuis
- 10 Tugas 05 : Truss tiga dimensi
- 11 Pertemuan 06 (Senin, 14 Desember 2020) : Muhasabah Pemahaman Studi Kasus
- 12 Sinopsis Tugas Besar : Aplikasi Metoda Numerik dalam Optimasi Desain Struktur Rangka Sederhana
- 13 Pertemuan 07 (Senin, 21 Desember 2020) : Aplikasi Metode Numerik dalam Kasus Optimasi
- 14 Pertemuan 08 (Senin, 28 Desember 2020) : Latihan Kasus Optimasi dengan Powell's Method
- 15 Tugas Besar Metode Numerik : Optimasi Desain Struktur Rangka (Truss) Sedarhana dengan Open Modelica
- 16 Ujian Akhir Semester (14 Januari 2021)
Materi sebelum UTS
Secara garis besar, terdapat tiga materi utama yang telah dipelajari pada perkuliahan-perkuliahan sebelum Ujian Tengah Semester (UTS) yang diajarkan oleh Pak Engkos. Ketiga materi tersebut adalah penencarian akar-akar persamaan, regresi linier, dan turunan numerik.
1. Pencarian akar-akar persamaan Untuk mencari akar-akar persamaan, digunakan 2 metode utama, yaitu metode tertutup (closed / bracketing method) dan metode terbuka (open method)
a. Metode tertutup : metode pencarian akar-akar dengan prinsip pengimpitan (menetapkan batas atas dan bawah). Persentase error juga akan didapat untuk mengukur tingkat akurasi dari iterasi yang dilakukan. Ada 3 metode pelaksanaannya, yaitu metode graphis, metode bisection, dan metode posisi salah (False-Position)
i. Metode grafik : menggunakan grafik untuk memperkirakan akar-akar dari suatu persamaan dengan memplotting suatu persamaan pada grafik.
ii. Metode bisection : metode incremental search method dengan mempersempit daerah pencarian akar-akar melalui batas atas dan batas bawah.
iii. Metode posisi salah (False-Position) : mirip dengan metode Bisection, kecuali dalam penentuan titik tengah dari batas-batas yang telah ditentukan dengan persamaan.
b. Metode Open Methods merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method
i. Metode Iterasi Sederhana (Fixed-Point Iteration) : memisahkan x dengan sebagian x yang lain sehingga diperoleh: x=g(x)
ii. Metode Newton-Raphson : menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut.
iii. Metode Secant : modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan).
Rangkuman rumus / persamaannya :
2.Regresi Linier Regresi linear : pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear. Persamaan umum Regresi Linier adalah sebagai berikut:
3. Turunan Numerik Turunan Numerik : penentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel, yang disajikan dalam 3 pendekatan sebagai berikut
Pertemuan 01 (Senin, 09 November 2020) : Pengenalan Aplikasi Open Modelica
Pada perkuliahan pertama setelah Ujian Tengah Semester yang diisi oleh Pak DAI, kami mempelajari mengenai penggunaan aplikasi ‘Open Modelica’, dimana perangkat lunak tersebut sangat berguna untuk fungsi permodelan dan simulasi open source yang biasanya kerap digunakan pada industri dan pembelajaran & penelitioan (akademis). Perangkat lunak tersebut dapat diunduh pada website resminya di [www.openmodelica.org]
Dengan Open Modelica, diharapkan kami dapat melakukan simulasi dengan menciptakan lingkungan permodelan secara komprehensif dan didistribusikan dalam bentuk kode sumber dan biner.
Selain itu, pada perkuliahan ini kami juga berdiskusi dengan beberapa konsep dasar dari Metode Numerik agar ilmu yang kami dapatkan dari perkuliahan Metode Numerik dapat dipahami dengan dalam dan dapat diaplikasikan secara maksimal.
Tugas 01 : Pelajari dan memberikan satu contoh aplikasi pada Open Modelica
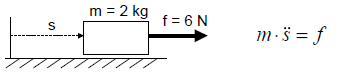
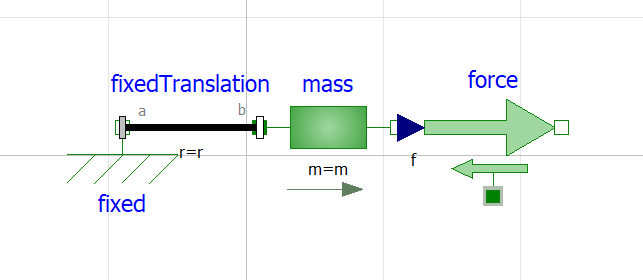
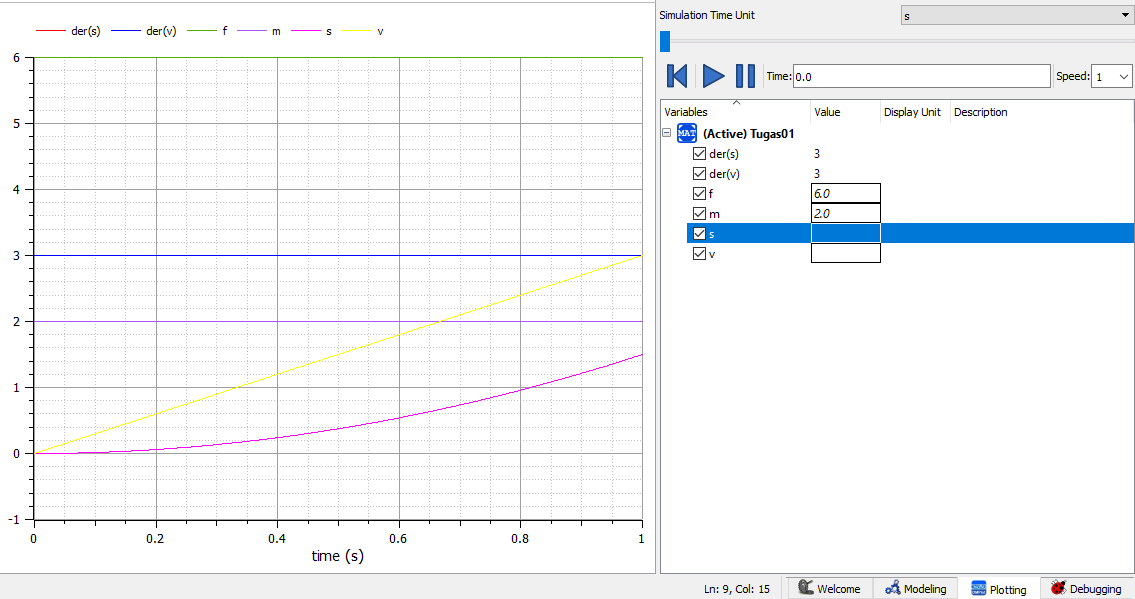
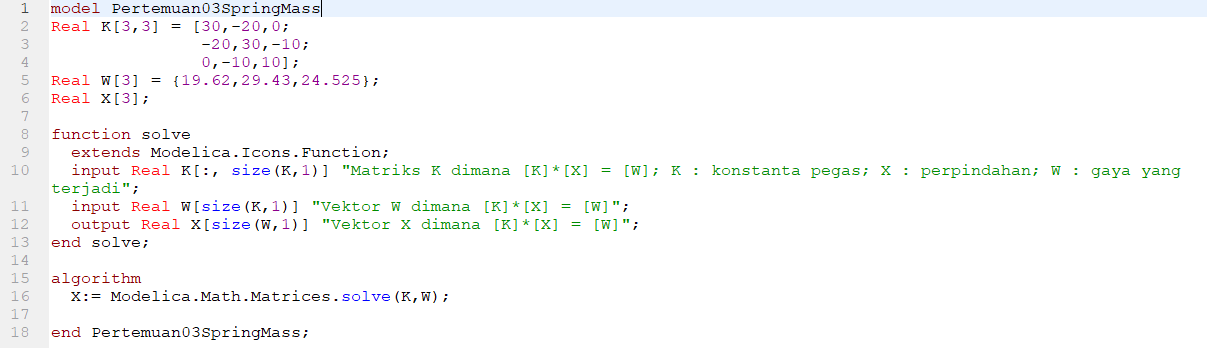
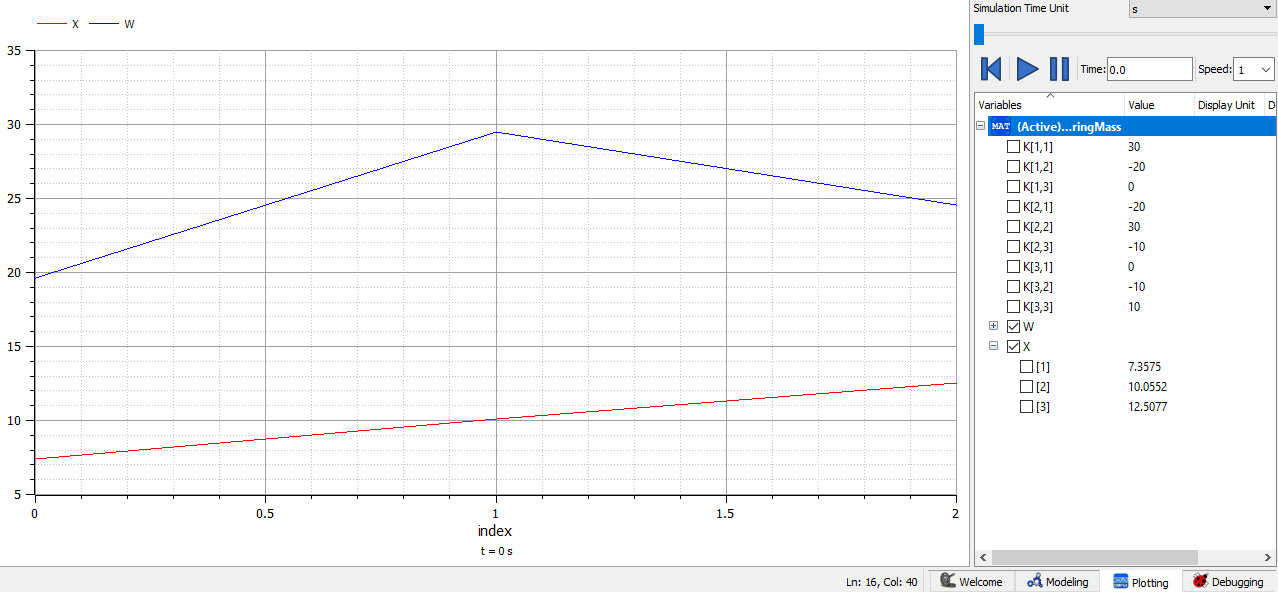
Pada tugas ini, saya mempelajari mengenai aplikasi Open Modelica dan melakukan percobaan pada satu contoh model sebagai berikut
Sesuai model tersebut, dapat dibuat coding dan hasilnya sebagai berikut
Pertemuan 02 (Senin, 16 November 2020) : Aplikasi mencari rata-rata dengan Open Modelica
Pada pertemuan ini, masing-masing dari kami diminta untuk menjelaskan mengenai tugas yang ditugaskan pada minggu lalu, sedangkan yang lainnya melakukan percobaan pada Open Modelica membuat pemograman mencari rata-rata dan mendapatkan hasil sebagai berikut
File:Hans Pertemuan02Model.png
Tugas 02 : Aplikasi Eliminasi Gauss untuk menyelesaikan persamaan-persamaan dengan Open Modelica
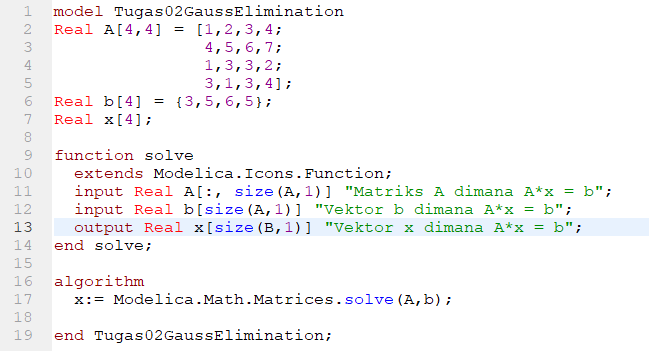
Pada tugas kedua, kami diminta untuk mengaplikasikan eliminasi Gauss pada Open Modelica untuk mencari akar-akar dari persamaan. Saya mengambil contoh soal dengan empat persamaan dan empat variabel sebagai berikut
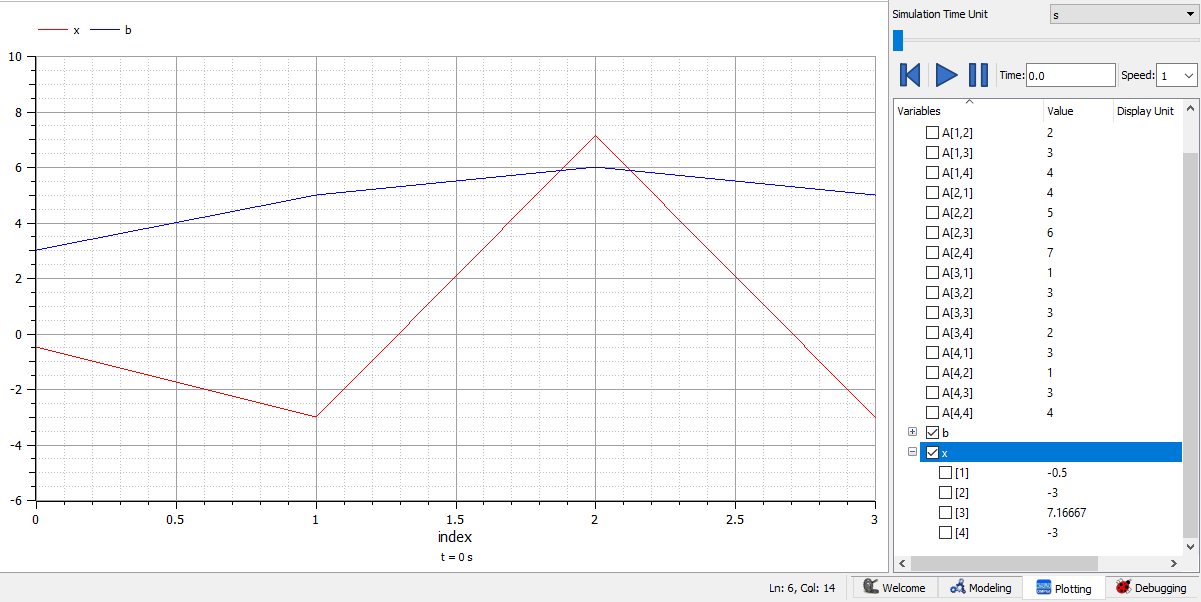
Sesuai contoh tersebut, dapat dibuat coding dan hasilnya sebagai berikut
Pertemuan 03 (Senin, 23 November 2020) :
Tugas 03 : Aplikasi analisis pada Open Modelica
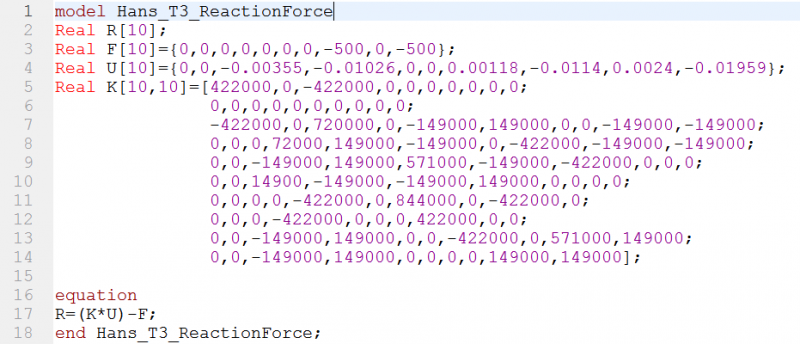
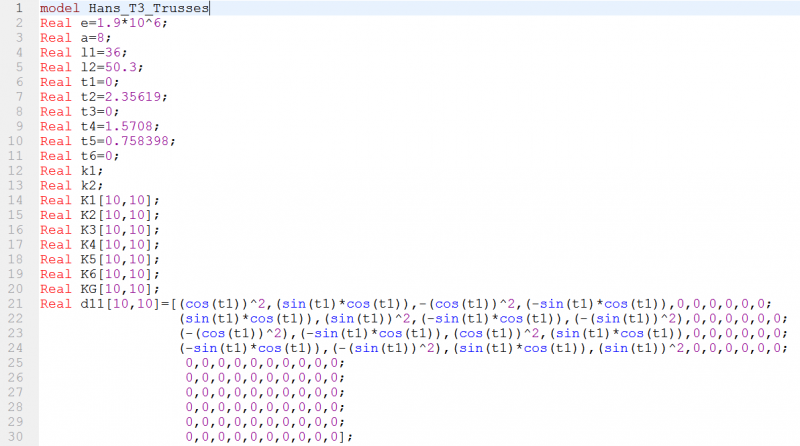
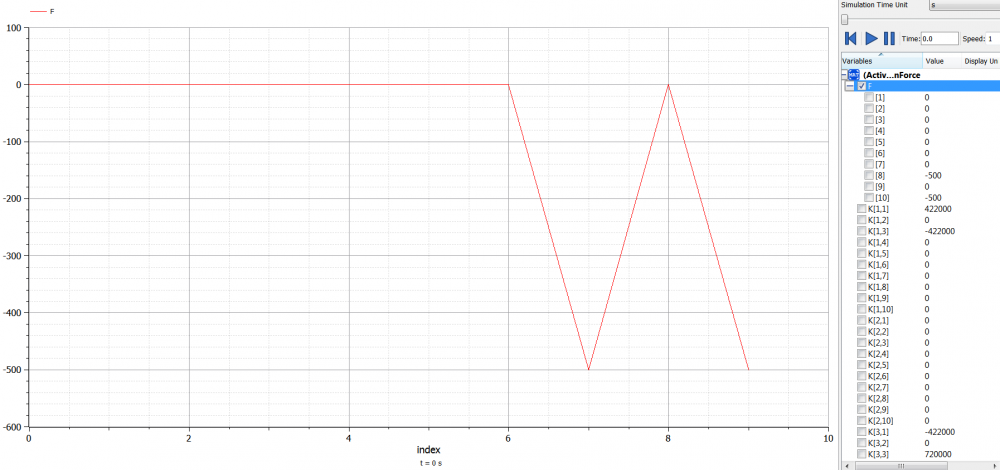
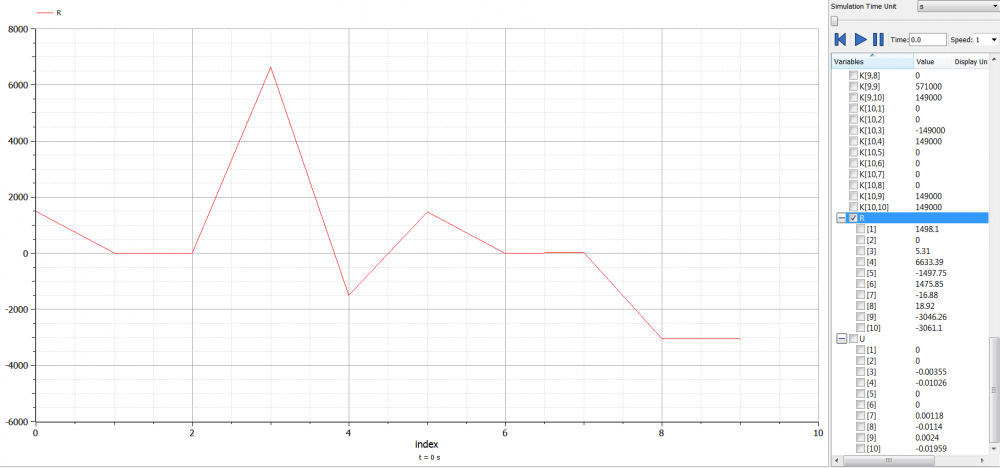
Sesuai dengan kasus contoh di atas, dapat dibuat pemograman (kode) sebagai berikut
Dari pemograman tersebut, didapatkan hasil simulasi sebagai berikut
Terlampir file Open Modelica untuk kedua model tersebut : [Reaction Forces] & [Trusses]
Pertemuan 04 (Senin, 30 November 2020)
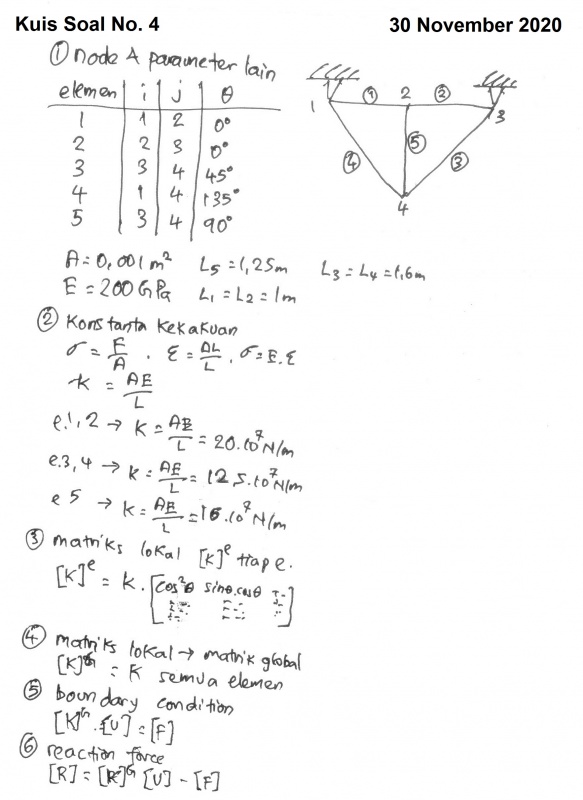
Kuis 01 : Truss
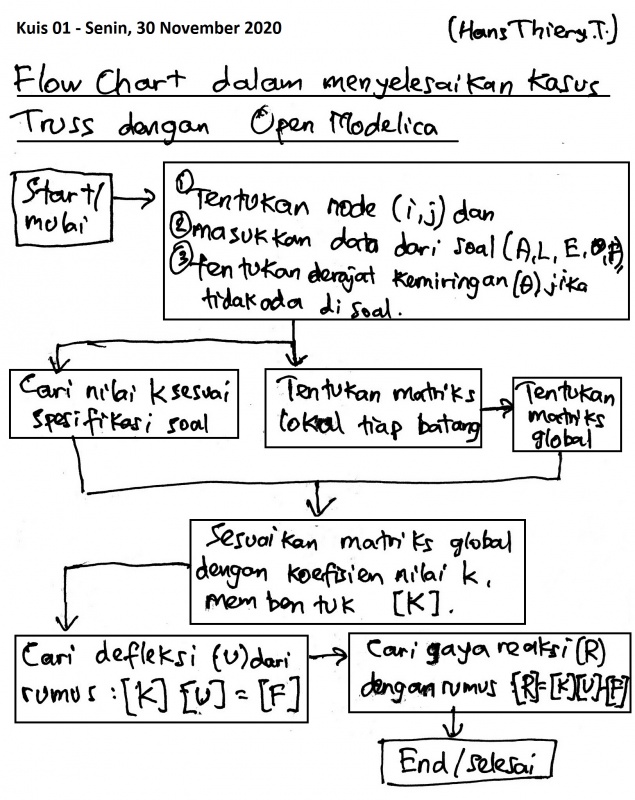
Untuk mnyelesaikan kasus Truss sebagai berikut
menggunakan Open Modelica, adapun tahapannya terlampir pada flow chart berikut
Pertemuan 05 (Senin, 07 Desember 2020) : Pembahasan Kuis
Pada pertemuan kali ini, kami melakukan pembahasan mengenai kuis yang telah kami kerjakan. Sebagai contoh, kami membahas coding yang telah dikerjakan oleh saudara Josiah Enrico dan Ahmad Mohammad Fahmi. Secara garis besar, perlu dibuat fungsi panggil yang digunakan pada algoritma looping dalam kedua soal model kuis tersebut, semuanya menggunakan Open Modelica.
Dari penjelasan tersebut, dapat didapatkan jawaban kuis sebagai berikut
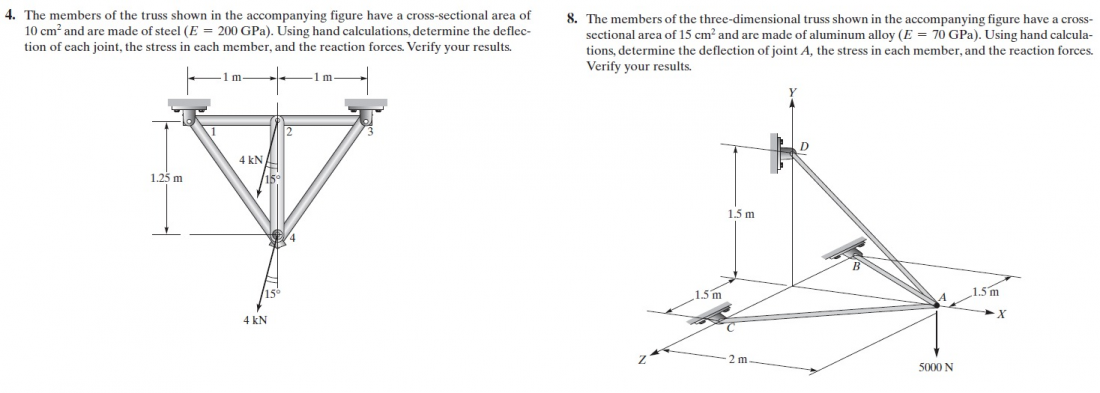
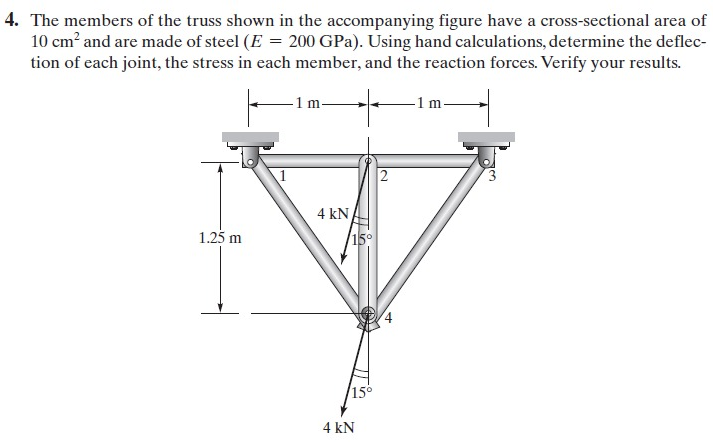
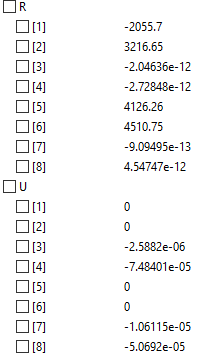
Soal nomor 1 (4) : truss dua dimensi
Dapat dikerjakan dengan flowchart :
Dari flowchart tersebut, dapat diaplikasikan pada coding sebagai berikut
- Fungsi Utama
class QuizSoal1
parameter Real [:,7] inisiasi = [1, 1, 2, 0, 10e-4, 200e9, 1.00;
2, 2, 3, 0, 10e-4, 200e9, 1.00;
3, 1, 4, 308.66, 10e-4, 200e9, 1.60;
4, 2, 4, 270.00, 10e-4, 200e9, 1.25;
5, 3, 4, 231.34, 10e-4, 200e9, 1.60];
parameter Integer [:,2] node = [1, 2;
2, 3;
1, 4;
2, 4;
3, 4];
parameter Integer y = size(node,1);
parameter Integer x = 2*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {1,3};
parameter Real [:,3] node_load = [1, 0, 0;
2, -1035.28, -3863.70;
3, 0, 0;
4, -1035.28, -3863.70];
parameter Real [2*(size(node_load,1))] load = {0,0,-1035.28,-3863.70,0,0,-1035.28,-3863.70};
Real [y] k;
Real [y,4,4] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
F = CheckForce(load,R);
end QuizSoal1;
- Fungsi Matriks Elemen (Stiffness Matrix Element)
function StiffnessMatrixElement
input Real [:,7] inisiasi_mat;
output Real [size(inisiasi_mat,1),4,4] Ke_mat;
protected
Real theta;
Real [3] StiffTrig;
Real [4,4] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
Real float_error = 10e-10;
algorithm
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / inisiasi_mat[i,7]) for i in 1:size(inisiasi_mat,1)};
for i in 1:size(inisiasi_mat,1) loop
StiffTrig := zeros(3);
StiffTrans := zeros(4,4);
theta := Modelica.SIunits.Conversions.from_deg(inisiasi_mat[i,4]);
// {cos^2, sin^2, sincos}
StiffTrig := {(Modelica.Math.cos(theta))^2,
(Modelica.Math.sin(theta))^2,
(Modelica.Math.sin(theta)*Modelica.Math.cos(theta))};
for t in 1:size(StiffTrig,1) loop
if abs(StiffTrig[t]) <= float_error then
StiffTrig[t] := 0;
end if;
end for;
StiffTrans := [ StiffTrig[1], StiffTrig[3], -1*StiffTrig[1], -1*StiffTrig[3];
StiffTrig[3], StiffTrig[2], -1*StiffTrig[3], -1*StiffTrig[2];
-1*StiffTrig[1], -1*StiffTrig[3], StiffTrig[1], StiffTrig[3];
-1*StiffTrig[3], -1*StiffTrig[2], StiffTrig[3], StiffTrig[2]];
for m in 1:4 loop
for n in 1:4 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
- Stiffness Matrix Global
function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,4,4] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop
Kg_mat[i,2*n[i,1],2*n[i,1]]:=Ke_mat[i,2,2];
Kg_mat[i,2*n[i,1]-1,2*n[i,1]-1]:=Ke_mat[i,1,1];
Kg_mat[i,2*n[i,1],2*n[i,1]-1]:=Ke_mat[i,2,1];
Kg_mat[i,2*n[i,1]-1,2*n[i,1]]:=Ke_mat[i,1,2];
Kg_mat[i,2*n[i,2],2*n[i,2]]:=Ke_mat[i,4,4];
Kg_mat[i,2*n[i,2]-1,2*n[i,2]-1]:=Ke_mat[i,3,3];
Kg_mat[i,2*n[i,2],2*n[i,2]-1]:=Ke_mat[i,4,3];
Kg_mat[i,2*n[i,2]-1,2*n[i,2]]:=Ke_mat[i,3,4];
Kg_mat[i,2*n[i,2],2*n[i,1]]:=Ke_mat[i,4,2];
Kg_mat[i,2*n[i,2]-1,2*n[i,1]-1]:=Ke_mat[i,3,1];
Kg_mat[i,2*n[i,2],2*n[i,1]-1]:=Ke_mat[i,4,1];
Kg_mat[i,2*n[i,2]-1,2*n[i,1]]:=Ke_mat[i,3,2];
Kg_mat[i,2*n[i,1],2*n[i,2]]:=Ke_mat[i,2,4];
Kg_mat[i,2*n[i,1]-1,2*n[i,2]-1]:=Ke_mat[i,1,3];
Kg_mat[i,2*n[i,1],2*n[i,2]-1]:=Ke_mat[i,2,3];
Kg_mat[i,2*n[i,1]-1,2*n[i,2]]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal;
- Sum of Stiffness Matrix Global
function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
- Implement Boundary Condition
function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:1 loop
KgB_met[2*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:1 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
- Gauss-Jordan
function GaussJordan
input Integer x;
input Real [x,x] KgB_met;
input Real [x] load_met;
output Real [x] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
- Reaction Force
function ReactionForce
input Integer x;
input Real [x,x] KgTot_met;
input Real [x] U_met;
input Real [x] load_met;
output Real [x] R_met;
algorithm
R_met := (KgTot_met*U_met)-load_met;
end ReactionForce;
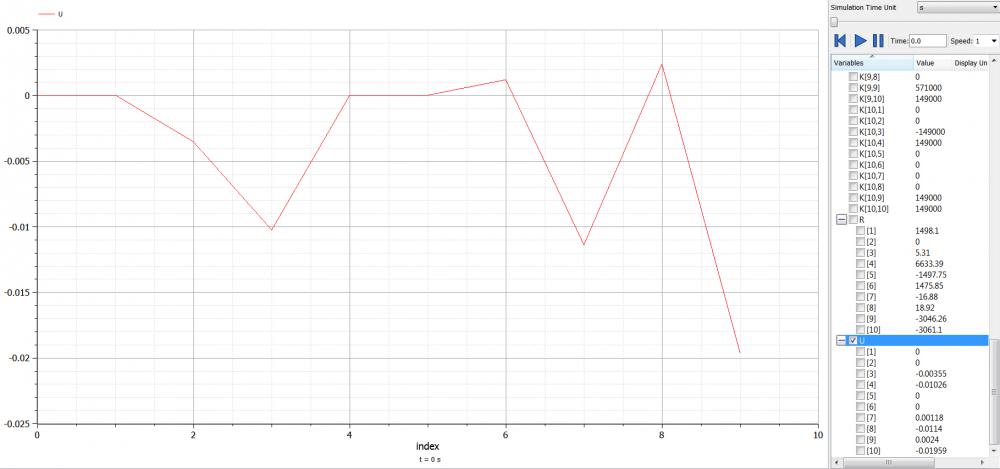
Simulasi dilakukan hanya pada fungsi utama, hasilnya sebagai berikut
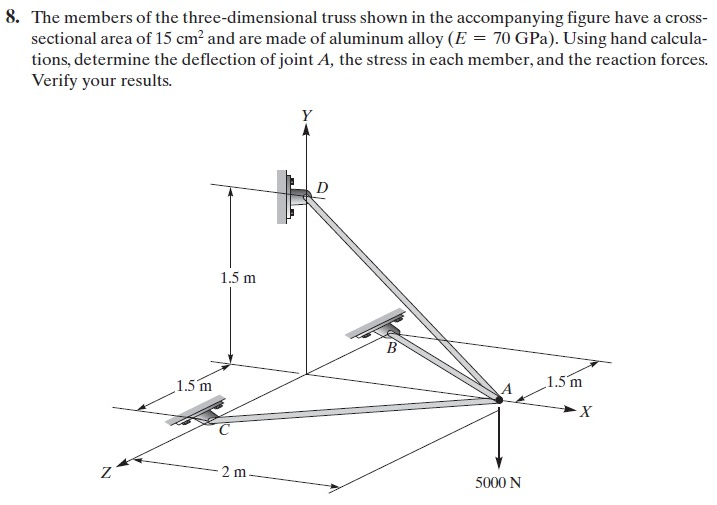
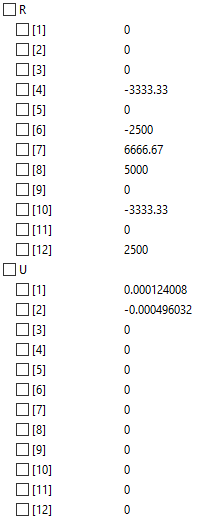
Soal nomor 2 (8) : truss tiga dimensi
Dapat dikerjakan dengan flowchart :
Dari flowchart tersebut, dapat diaplikasikan pada coding sebagai berikut
- Fungsi Utama
class QuizSoal2
parameter Real [:,7] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5;
2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5;
3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {2,3,4};
parameter Real [:,4] node_load = [1, 0, -5000, 0;
2, 0, 0, 0;
3, 0, 0, 0;
4, 0, 0, 0];
parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
F = CheckForce(load,R);
end QuizSoal2;
- Fungsi Matriks Elemen (Stiffness Matrix Element)
function StiffnessMatrixElement2
input Real [:,9] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};
for i in 1:size(inisiasi_mat,1) loop
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
cos_x := inisiasi_mat[i,4];
cos_y := inisiasi_mat[i,5];
cos_z := inisiasi_mat[i,6];
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement2;
- Stiffness Matrix Global
function StiffnessMatrixGlobal2
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal2;
- Sum of Stiffness Matrix Global
function SumStiffnessMatrixGlobal2
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal2;
- Implement Boundary Condition
function BoundaryStiffnessMatrixGlobal2
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal2;
- Gauss-Jordan
function GaussJordan2
input Integer x;
input Real [x,x] KgB_met;
input Real [x] load_met;
output Real [x] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan2;
- Reaction Force
function ReactionForce2
input Integer x;
input Real [x,x] KgTot_met;
input Real [x] U_met;
input Real [x] load_met;
output Real [x] R_met;
algorithm
R_met := (KgTot_met*U_met)-load_met;
end ReactionForce2;
Simulasi dilakukan hanya pada fungsi utama, hasilnya sebagai berikut
Tugas 05 : Truss tiga dimensi
Sesuai soal di atas, dapat diaplikasikan pada coding sebagai berikut
- Fungsi Utama
class Hans_Metnum_Tugas5_Main
parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data
2, 0, 0, -6, 1.56, 10.6e6;
3, 0, 6, -3, 1.56, 10.6e6;
4, -6, 0, -3, 1.56, 10.6e6;
5, -6, 6, 0, 1.56, 10.6e6;
6, 0, 6, 3, 1.56, 10.6e6];
parameter Integer [size(inisiasi,1),2] node = [1, 2;
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
parameter Integer n = 4; //isi sesuai data
parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data
parameter Integer [:] Boundary_xy = {4}; //isi sesuai data
parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
parameter Integer [:] Boundary_x = {3}; //isi sesuai data
parameter Integer [:] Boundary_y = {0}; //isi sesuai data
parameter Integer [:] Boundary_z = {0}; //isi sesuai data
parameter Real [3*n] load = {0, 0, 0, //isi sesuai data
0, -200, 0,
0, 0, 0,
0, 0, 0};
Real [size(inisiasi,1)] L;
Real [size(inisiasi,1)] k;
Real [size(inisiasi,1),6,6] Ke;
Real [size(inisiasi,1),3*n,3*n] Kg;
Real [3*n,3*n] KgTot;
Real [3*n,3*n] KgB;
Real [3*n] U;
Real [3*n] R;
Real [3] F;
equation
L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(n, node, Ke);
KgTot = SumStiffnessMatrixGlobal(Kg);
KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z);
U = GaussJordan(KgB, load);
R = ReactionForce(KgTot, U, load);
F = CheckForce(load,R);
end Hans_Metnum_Tugas5_Main;
- Fungsi Matriks Elemen (Stiffness Matrix Element)
function Hans_Metnum_Tugas5_StiffnessMatrixElement
input Real [:,6] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)};
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)};
for i in 1:size(inisiasi_mat,1) loop
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
cos_x := inisiasi_mat[i,2]/L[i];
cos_y := inisiasi_mat[i,3]/L[i];
cos_z := inisiasi_mat[i,4]/L[i];
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end Hans_Metnum_Tugas5_StiffnessMatrixElement;
- Stiffness Matrix Global
function Hans_Metnum_Tugas5_StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
Kg_mat:=zero(size(ke_mat,1),3*x,3*x);
for i in 1:size(Ke_mat,1) loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
end for;
end Hans_Metnum_Tugas5_StiffnessMatrixGlobal;
- Sum of Stiffness Matrix Global
function Hans_Metnum_Tugas5_SumStiffnessMatrixGlobal
input Real [:,:,:] Kg_mat;
output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat;
algorithm
for a in 1:size(Kg_mat,2) loop
for b in 1:size(Kg_mat,2) loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end Hans_Metnum_Tugas5_SumStiffnessMatrixGlobal;
- Implement Boundary Condition
function Hans_Metnum_Tugas5_BoundaryStiffnessMatrixGlobal
input Real [:,:] KgTot_met;
input Integer[:] Boundary_xyz;
input Integer[:] Boundary_xy;
input Integer[:] Boundary_xz;
input Integer[:] Boundary_yz;
input Integer[:] Boundary_x;
input Integer[:] Boundary_y;
input Integer[:] Boundary_z;
output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met;
algorithm
for a in 1:size(KgTot_met,1) loop
for b in 1:size(KgTot_met,1) loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
if Boundary_xyz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xyz,1) loop
for b in 0:2 loop
KgB_met[3*(Boundary_xyz[a])-b,i]:=0;
KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xy[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xy,1) loop
for b in 1:2 loop
KgB_met[3*(Boundary_xy[a])-b,i]:=0;
KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xz,1) loop
for b in 0:2:2 loop
KgB_met[3*(Boundary_xz[a])-b,i]:=0;
KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_yz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_yz,1) loop
for b in 0:1 loop
KgB_met[3*(Boundary_yz[a])-b,i]:=0;
KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_x[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_x,1) loop
KgB_met[3*(Boundary_x[a])-2,i]:=0;
KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1;
end for;
end for;
end if;
if Boundary_y[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_y,1) loop
KgB_met[3*(Boundary_y[a])-1,i]:=0;
KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1;
end for;
end for;
end if;
if Boundary_z[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_z,1) loop
KgB_met[3*Boundary_z[a],i]:=0;
KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1;
end for;
end for;
end if;
end Hans_Metnum_Tugas5_BoundaryStiffnessMatrixGlobal;
- Gauss-Jordan
function Hans_Metnum_Tugas5_GaussJordan
input Real [:,:] KgB_met;
input Real [size(KgB_met,1)] load_met;
output Real [size(KgB_met,1)] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:size(KgB_met,1) loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end Hans_Metnum_Tugas5_GaussJordan;
- Reaction Force
function Hans_Metnum_Tugas5_ReactionForce
input Integer x;
input Real [:,:] KgTot_met;
input Real [size(KgTot_met,1)] U_met;
input Real [size(KgTot_met,1)] load_met;
output Real [x] R_met;
protected Real float_error = 10e-10;
algorithm
R_met := (KgTot_met*U_met)-load_met;
for t in 1:size(KgTot_met,1) loop
if abs(R_met[t]) <= float_error then
R_met[t] := 0;
end if;
end for;
end Hans_Metnum_Tugas5_ReactionForce;
- Pengecekan kesetimbangan gaya (resultan gaya = 0)
function Hans_Metnum_Tugas5_CheckForce
input Real [:] load;
input Real [size(load,1)] R;
output Real [3] F;
protected Real float_error = 10e-10;
protected
Real load_x;
Real load_y;
Real load_z;
Real R_x;
Real R_y;
Real R_z;
algorithm
load_x := sum({load[i] for i in 1:3:(size(load,1)-2)});
load_y := sum({load[i] for i in 2:3:(size(load,1)-1)});
load_z := sum({load[i] for i in 3:3:size(load,1)});
R_x := sum({R[i] for i in 1:3:(size(load,1)-2)});
R_y := sum({R[i] for i in 2:3:(size(load,1)-1)});
R_z := sum({R[i] for i in 3:3:size(load,1)});
F[1] := load_x + R_x;
F[2] := load_y + R_y;
F[3] := load_z + R_z;
for i in 1:3 loop
if abs(F[i]) <= float_error then
F[i] := 0;
end if;
end for;
end Hans_Metnum_Tugas5_CheckForce;
Simulasi dilakukan hanya pada fungsi utama, hasilnya sebagai berikut
Didapatkan resultan gaya sama dengan nol
Pertemuan 06 (Senin, 14 Desember 2020) : Muhasabah Pemahaman Studi Kasus
Pada perkuliahan ini, kami melakukan muhasabah diri sendiri terhadap pemahaman tentang metode numerik yang telah dipelajari pada semester ini, sebagai kesimpulan muhasabah saya adalah sebagai berikut
Pada pandangan saya, pemahaman saya mengenai dasar-dasar metode numerik sesuai pelajaran sebelum UTS sudah cukup baik untuk dilanjutkan pada tahapan selanjutnya, yaitu penerapan pada Open Modelica. Namun, selain pemahaman numerik, pemahaman mengenai dasar-dasar fisika, termasuk teori, hukum, dan fenomena haris dapat dipahami sebelum dilakukan aplikasi simulasi pada Open Modelica dengan membuat model matematika yang sesuai. Dengan Open Modelica dan aplikasi-aplikasi lainnya, kami dapat menyelesaikan permasalahan teknik secara mudah, tanpa perhitungan manual yang sangat panjang dan rawan terhadap kesilapan. Akan tetapi, bahasa pemograman Open Modelica yang cukup baru dan asing bagi saya, membuat saya harus mempelajarinya dari awal dan menyeluruh agar dapat menggunakannya secara maksimal dan efisien. Dengan pemahaman tersebut, saya dapat dengan mudah menyelesaikan berbagai masalah teknik, sesuai dengan prosedur atau flowchart penyelesaiannya. Saya berharap saya dapat memahaminya dengan baik, sehingga dapat mempraktikkannya ke depannya dan memenuhi kriteria kelulusan, serta menguasai ilmu yang diharapkan dimiliki oleh seorang mahasiswa teknik mesin.
Sinopsis Tugas Besar : Aplikasi Metoda Numerik dalam Optimasi Desain Struktur Rangka Sederhana
Pada tugas besar Mata Kuliah Metode Numerik akan bertema optimasi desain struktur rangka. Aplikasi tersebut akan dilakukan dengan Open Modelica sesuai pemaparan / pembelajaran pada perkuliahan. Dengan pemograman tersebut, dapat dilakukan optimasi pada susunan desain rangka dengan pemograman yang efisien dan ringan.
Pertemuan 07 (Senin, 21 Desember 2020) : Aplikasi Metode Numerik dalam Kasus Optimasi
Pada perkuliahan ini, Kami mendapatkan pemaparan mengenai topik Aplikasi Metode Numerik dalam Optimasi Desain Struktur Rangka Sederhana yang akan menjadi topik tugas besar. Secara garis besar, tujuan yang hendak dicapai adalah untuk menentukan material yang optimal dan murah untuk rangka sederhana (Truss).
Setelah itu Ibu Candra memberikan tutorial optimasi Bracket Optimization Using Golden Ratio, yaitu dengan fungsi yang memiliki fungsi maksimum dan minimum lokal dan global. Sebagai contoh, kami melakukan optimasi pada soal : Tentukan nilai f(x) maksimum dengan metode golden ration dari fungsi f(x) = 2sinx-x^2/10
Dengan contoh tersebut dapat dilakukan coding sebagai berikut
model Hans_Metnum_bracket_optimation
parameter Integer n=8;
Real x1 [n];
Real x2 [n];
Real xup;
Real xlow;
Real d;
Real f1 [n];
Real f2 [n];
Real xopt;
Real yopt;
algorithm
xup :=4;
xlow :=0;
for i in (1:n) loop
d:=(5^(1/2)-1)/2*(xup-xlow);
x1[i] := xlow+d;
x2[i] := xup-d;
f1[i] := f_obj3(x1[i]);
f2[i] := f_obj3(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow:= x2[i];
xopt:= xup;
yopt:= f1[i];
else
xlow := xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end Hans_Metnum_bracket_optimation;
dengan fungsi panggil:
function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:=2*Math.sin(x)-x^2/10; end f_obj3;
Dari pengkodingan tersebut akan didapatkan f(x) maksimum yang secara konsep mirip dengan apa yang akan dilakukan pada tugas besar.
Pertemuan 08 (Senin, 28 Desember 2020) : Latihan Kasus Optimasi dengan Powell's Method
Tugas Besar Metode Numerik : Optimasi Desain Struktur Rangka (Truss) Sedarhana dengan Open Modelica
Latar Belakang
Optimasi pada suatu desain sangat diperlukan agar dapat menghasilkan desain yang paling optimal, sehingga didapatkan harga yang paling murah dengan kualitas mumpuni atau sesuai dengan spesifikasi target pemakaian
Tujuan
Mendapatkan desain dengan harga paling murah dan spesifikasi atau kemampuan mumpuni untuk target penggunaan (Spesifikasi material, luas, dan harga yang optimal)
Ilustrasi Model
Data yang Diketahui
Jenis model : Rangka batang (bar element) dengan struktur batang
Dimensi Rangka Batang : 0.6m x 0.75m x 1.8m (p x l x t)
F1 = 2000 N
F2 = 1000 N
Ketentuan
- Optimasi secara harga temurah dengan faktor berubah kekuatan dan area
- Tujuan optimasi : Displacement U minimum (kuat), Cross-area minimum, dan Nilai E dan A (murah)
Asumsi
- Lantai dasar fix
- Tidak ada bending
- Beban terdistribusi, sehingga dibagi dua pada setiap sudut
Metodologi
Dalam pengerjaan tugas besar ini, akan dibuat pencodingan sesuai model yang diberikan dengan tujuan optimasi mencari material dan ukuran yang paling cocok
Prosedur
1. Menentukan Jarak Node dengan asumsi sendiri
2. Menentukan Batasan Displacement dengan asumsi sendiri
3. Mengoptimisasi E (elastisitas material), A (luas), dan harga sesuai standar / referensi dari produsen dilakukan dengan 2 fase, yaitu
a. Material bervariasi, area tetap untuk mencari material optimum b. Material tetap, luas bervariasi untuk mencari dimensi atau ukuran optimum
menggunakan cara Curve Fitting dan Golden Section
4. Memilih E/A untuk jadi patokan minimum dengan harga keseluruhan termurah (optimal)
Perencanaan Waktu
Ditargetkan untuk selesai sebelum tanggal pengumpulan terakhir
Koding
Trusses Modelling
model Hans_Metnum_TubesMain
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=nilai yield strength; //Yield Strength (Pa)
parameter Real Area=nilai luas';; //Area L Profile
parameter Real Elas=nilai elastisitas; //Elasticity (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Hans_Metnum_TubesMain;
Curve Fitting
class Curvefitting
parameter Real X[jumlah plot]={plot};
parameter Real Y[jumlah plot]={plot};
Real Coe[3];
algorithm
Coe:=Curve_Fitting(X,Y,2);
end Curvefitting;
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
Golden Section
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Hasil
Dengan optimasi, didapatkan :
Kesimpulan : Luas optimal yang didapatkan adalah 0.00154 m^2
Dengan optimasi, didapatkan :
Kesimpulan : Elastisitas optimal yang didapatkan adalah 203 GPa
Ujian Akhir Semester (14 Januari 2021)
Berikut adalah jawaban Ujian Akhir Semester Mata Kuliah Metode Numerik 03 saya