Difference between revisions of "M. Raja"
(→UAS) |
|||
| (87 intermediate revisions by the same user not shown) | |||
| Line 82: | Line 82: | ||
</div> | </div> | ||
| + | ===Pertemuan ke-3=== | ||
====Tugas Minggu 3==== | ====Tugas Minggu 3==== | ||
| − | + | [[File:Soal Trusses 1 Tugasku.png|450px|thumb|center]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | // | + | model Trusses_PR |
| − | parameter Real | + | parameter Integer N=10; //Global matrice = 2*points connected |
| − | Real | + | parameter Real A=8; |
| − | Real | + | parameter Real E=1.9e6; |
| − | + | Real G[N,N]; //global | |
| − | + | Real Ginitial[N,N]; //global | |
| − | Real | + | Real Sol[N]; //global dispplacement |
| + | Real X[N]={0,0,0,0,0,0,0,-500,0,-500}; | ||
| + | Real R[N]; //global reaction force | ||
| + | Real SolMat[N,1]; | ||
| + | Real XMat[N,1]; | ||
| − | // | + | //boundary coundition |
| − | + | Integer b1=1; | |
| − | + | Integer b2=3; | |
| − | |||
| − | Integer | ||
| − | Integer | ||
| − | |||
| − | //truss | + | //truss 1 |
| − | parameter Real | + | parameter Real X1=0; //degree between truss |
| − | Real | + | Real k1=A*E/36; |
| − | Real | + | Real K1[4,4]; //stiffness matrice |
| − | Integer | + | Integer p1a=1; |
| − | Integer | + | Integer p1b=2; |
| − | Real | + | Real G1[N,N]; |
| − | //truss | + | //truss 2 |
| − | parameter Real | + | parameter Real X2=135; //degree between truss |
| − | Real | + | Real k2=A*E/50.912; |
| − | Real | + | Real K2[4,4]; //stiffness matrice |
| − | Integer | + | Integer p2a=2; |
| − | Integer | + | Integer p2b=3; |
| − | Real | + | Real G2[N,N]; |
| − | //truss | + | //truss 3 |
| − | parameter Real | + | parameter Real X3=0; //degree between truss |
| − | Real | + | Real k3=A*E/36; |
| − | Real | + | Real K3[4,4]; //stiffness matrice |
| − | Integer | + | Integer p3a=3; |
| − | Integer | + | Integer p3b=4; |
| − | Real | + | Real G3[N,N]; |
| − | //truss | + | //truss 4 |
| − | parameter Real | + | parameter Real X4=90; //degree between truss |
| − | Real | + | Real k4=A*E/36; |
| − | Real | + | Real K4[4,4]; //stiffness matrice |
| − | Integer | + | Integer p4a=2; |
| − | Integer | + | Integer p4b=4; |
| − | Real | + | Real G4[N,N]; |
| − | / | + | //truss 5 |
| − | + | parameter Real X5=45; //degree between truss | |
| − | */ | + | Real k5=A*E/50.912; |
| + | Real K5[4,4]; //stiffness matrice | ||
| + | Integer p5a=2; | ||
| + | Integer p5b=5; | ||
| + | Real G5[N,N]; | ||
| − | + | //truss 6 | |
| + | parameter Real X6=0; //degree between truss | ||
| + | Real k6=A*E/36; | ||
| + | Real K6[4,4]; //stiffness matrice | ||
| + | Integer p6a=4; | ||
| + | Integer p6b=5; | ||
| + | Real G6[N,N]; | ||
| − | / | + | /* |
| − | + | for each truss, please ensure pXa is lower then pXb (X represents truss element number) | |
| − | + | */ | |
| − | + | algorithm | |
| − | |||
| − | + | //creating global matrice | |
| − | + | K1:=Kekakuan_Matrix(X1); | |
| + | G1:=k1*Local_Global(K1,N,p1a,p1b); | ||
| − | + | K2:=Kekakuan_Matrix(X2); | |
| − | + | G2:=k2*Local_Global(K2,N,p2a,p2b); | |
| − | + | K3:=Kekakuan_Matrix(X3); | |
| − | + | G3:=k3*Local_Global(K3,N,p3a,p3b); | |
| − | + | K4:=Kekakuan_Matrix(X4); | |
| − | + | G4:=k4*Local_Global(K4,N,p4a,p4b); | |
| − | + | K5:=Kekakuan_Matrix(X5); | |
| − | + | G5:=k5*Local_Global(K5,N,p5a,p5b); | |
| − | //implementing boundary condition | + | K6:=Kekakuan_Matrix(X6); |
| − | for i in 1:N loop | + | G6:=k6*Local_Global(K6,N,p6a,p6b); |
| − | + | ||
| − | + | G:=G1+G2+G3+G4+G5+G6; | |
| − | + | Ginitial:=G; | |
| − | + | ||
| − | end for; | + | //implementing boundary condition |
| + | for i in 1:N loop | ||
| + | G[2*b1-1,i]:=0; | ||
| + | G[2*b1,i]:=0; | ||
| + | G[2*b2-1,i]:=0; | ||
| + | G[2*b2,i]:=0; | ||
| + | end for; | ||
| − | G[2*b1-1,2*b1-1]:=1; | + | G[2*b1-1,2*b1-1]:=1; |
| − | G[2*b1,2*b1]:=1; | + | G[2*b1,2*b1]:=1; |
| − | G[2*b2-1,2*b2-1]:=1; | + | G[2*b2-1,2*b2-1]:=1; |
| − | G[2*b2,2*b2]:=1; | + | G[2*b2,2*b2]:=1; |
| − | //solving displacement | + | //solving displacement |
| − | Sol:=Gauss_Jordan(N,G,X); | + | Sol:=Gauss_Jordan(N,G,X); |
| − | //solving reaction force | + | //solving reaction force |
| − | SolMat:=matrix(Sol); | + | SolMat:=matrix(Sol); |
| − | XMat:=matrix(X); | + | XMat:=matrix(X); |
| − | R:=Reaction_Trusses1(N,Ginitial,SolMat,XMat); | + | R:=Reaction_Trusses1(N,Ginitial,SolMat,XMat); |
| − | end Trusses_PR; | + | end Trusses_PR; |
| − | ==== | + | ====class Trusses==== |
| − | + | [[File:M. Raja1.jpg|450px|thumb|center]] | |
| − | parameter Integer N=8; //Global matrice = 2*points connected | + | parameter Integer N=8; //Global matrice = 2*points connected |
| − | parameter Real A=0.001; //Area m^2 | + | parameter Real A=0.001; //Area m^2 |
| − | parameter Real E=200e9; //Pa | + | parameter Real E=200e9; //Pa |
| − | Real G[N,N]; //global | + | Real G[N,N]; //global |
| − | Real Ginitial[N,N]; //global | + | Real Ginitial[N,N]; //global |
| − | Real Sol[N]; //global displacement | + | Real Sol[N]; //global displacement |
| − | Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; | + | Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; |
| − | Real R[N]; //global reaction force | + | Real R[N]; //global reaction force |
| − | Real SolMat[N,1]; | + | Real SolMat[N,1]; |
| − | Real XMat[N,1]; | + | Real XMat[N,1]; |
| − | //boundary condition | + | //boundary condition |
| − | Integer b1=1; | + | Integer b1=1; |
| − | Integer b2=3; | + | Integer b2=3; |
| − | //truss 1 | + | //truss 1 |
| − | parameter Real X1=0; //degree between truss | + | parameter Real X1=0; //degree between truss |
| − | Real k1=A*E/1; | + | Real k1=A*E/1; |
| − | Real K1[4,4]; //stiffness matrice | + | Real K1[4,4]; //stiffness matrice |
| − | Integer p1a=1; | + | Integer p1a=1; |
| − | Integer p1b=2; | + | Integer p1b=2; |
| − | Real G1[N,N]; | + | Real G1[N,N]; |
| − | //truss 2 | + | //truss 2 |
| − | parameter Real X2=0; //degree between truss | + | parameter Real X2=0; //degree between truss |
| − | Real k2=A*E/1; | + | Real k2=A*E/1; |
| − | Real K2[4,4]; //stiffness matrice | + | Real K2[4,4]; //stiffness matrice |
| − | Integer p2a=2; | + | Integer p2a=2; |
| − | Integer p2b=3; | + | Integer p2b=3; |
| − | Real G2[N,N]; | + | Real G2[N,N]; |
| − | //truss 3 | + | //truss 3 |
| − | parameter Real X3=90; //degree between truss | + | parameter Real X3=90; //degree between truss |
| − | Real k3=A*E/1.25; | + | Real k3=A*E/1.25; |
| − | Real K3[4,4]; //stiffness matrice | + | Real K3[4,4]; //stiffness matrice |
| − | Integer p3a=2; | + | Integer p3a=2; |
| − | Integer p3b=4; | + | Integer p3b=4; |
| − | Real G3[N,N]; | + | Real G3[N,N]; |
| − | //truss 4 | + | //truss 4 |
| − | parameter Real X4=90+38.6598; //degree between truss | + | parameter Real X4=90+38.6598; //degree between truss |
| − | Real k4=A*E/1.6; | + | Real k4=A*E/1.6; |
| − | Real K4[4,4]; //stiffness matrice | + | Real K4[4,4]; //stiffness matrice |
| − | Integer p4a=1; | + | Integer p4a=1; |
| − | Integer p4b=4; | + | Integer p4b=4; |
| − | Real G4[N,N]; | + | Real G4[N,N]; |
| − | //truss 5 | + | //truss 5 |
| − | parameter Real X5=90-38.6598; //degree between truss | + | parameter Real X5=90-38.6598; //degree between truss |
| − | Real k5=A*E/1.6; | + | Real k5=A*E/1.6; |
| − | Real K5[4,4]; //stiffness matrice | + | Real K5[4,4]; //stiffness matrice |
| − | Integer p5a=3; | + | Integer p5a=3; |
| − | Integer p5b=4; | + | Integer p5b=4; |
| − | Real G5[N,N]; | + | Real G5[N,N]; |
| − | /* | + | /* |
| − | for each truss, please ensure pXa is lower then pXb (X represents truss element number) | + | for each truss, please ensure pXa is lower then pXb (X represents truss |
| − | */ | + | element number) |
| + | */ | ||
| − | algorithm | + | algorithm |
| − | //creating global matrice | + | //creating global matrice |
| − | K1:=Kekakuan_Matrix(X1); | + | K1:=Kekakuan_Matrix(X1); |
| − | G1:=k1*Local_Global(K1,N,p1a,p1b); | + | G1:=k1*Local_Global(K1,N,p1a,p1b); |
| − | K2:=Kekakuan_Matrix(X2); | + | K2:=Kekakuan_Matrix(X2); |
| − | G2:=k2*Local_Global(K2,N,p2a,p2b); | + | G2:=k2*Local_Global(K2,N,p2a,p2b); |
| − | K3:=Kekakuan_Matrix(X3); | + | K3:=Kekakuan_Matrix(X3); |
| − | G3:=k3*Local_Global(K3,N,p3a,p3b); | + | G3:=k3*Local_Global(K3,N,p3a,p3b); |
| − | K4:=Kekakuan_Matrix(X4); | + | K4:=Kekakuan_Matrix(X4); |
| − | G4:=k4*Local_Global(K4,N,p4a,p4b); | + | G4:=k4*Local_Global(K4,N,p4a,p4b); |
| − | K5:=Kekakuan_Matrix(X5); | + | K5:=Kekakuan_Matrix(X5); |
| − | G5:=k5*Local_Global(K5,N,p5a,p5b); | + | G5:=k5*Local_Global(K5,N,p5a,p5b); |
| − | G:=G1+G2+G3+G4+G5; | + | G:=G1+G2+G3+G4+G5; |
| − | Ginitial:=G; | + | Ginitial:=G; |
| − | //implementing boundary condition | + | //implementing boundary condition |
| − | for i in 1:N loop | + | for i in 1:N loop |
G[2*b1-1,i]:=0; | G[2*b1-1,i]:=0; | ||
G[2*b1,i]:=0; | G[2*b1,i]:=0; | ||
G[2*b2-1,i]:=0; | G[2*b2-1,i]:=0; | ||
G[2*b2,i]:=0; | G[2*b2,i]:=0; | ||
| − | end for; | + | end for; |
| − | G[2*b1-1,2*b1-1]:=1; | + | G[2*b1-1,2*b1-1]:=1; |
| − | G[2*b1,2*b1]:=1; | + | G[2*b1,2*b1]:=1; |
| − | G[2*b2-1,2*b2-1]:=1; | + | G[2*b2-1,2*b2-1]:=1; |
| − | G[2*b2,2*b2]:=1; | + | G[2*b2,2*b2]:=1; |
| − | //solving displacement | + | //solving displacement |
| − | Sol:=Gauss_Jordan(N,G,X); | + | Sol:=Gauss_Jordan(N,G,X); |
| − | //solving reaction force | + | //solving reaction force |
| − | SolMat:=matrix(Sol); | + | SolMat:=matrix(Sol); |
| − | XMat:=matrix(X); | + | XMat:=matrix(X); |
| − | R:=Reaction_Trusses1(N,Ginitial,SolMat,XMat); | + | R:=Reaction_Trusses1(N,Ginitial,SolMat,XMat); |
| − | end Trusses; | + | end Trusses; |
====Fungsi Panggil==== | ====Fungsi Panggil==== | ||
| − | function Kekakuan_Matrix | + | function Kekakuan_Matrix |
| − | input Real A; | + | input Real A; |
| − | Real Y; | + | Real Y; |
| − | output Real X[4,4]; | + | output Real X[4,4]; |
| − | Real float_error = 10e-10; | + | Real float_error = 10e-10; |
| − | final constant Real pi=2*Modelica.Math.asin(1.0); | + | final constant Real pi=2*Modelica.Math.asin(1.0); |
| − | algorithm | + | algorithm |
| − | Y:=A/180*pi; | + | Y:=A/180*pi; |
| − | X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | + | X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),- (Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y); |
| + | |||
| + | Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,- Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2; | ||
| + | |||
| + | -(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y), (Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | -Modelica.Math.cos(Y)*Modelica.Math.sin(Y),- (Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y), (Modelica.Math.sin(Y))^2]; | ||
| − | + | for i in 1:4 loop | |
| + | for j in 1:4 loop | ||
| + | if abs(X[i,j]) <= float_error then | ||
| + | X[i,j] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| − | + | end Kekakuan_Matrix; | |
| − | + | ====Function==== | |
| − | for i in 1: | + | function Local_Global |
| − | + | input Real Y[4,4]; | |
| − | if abs(X[i | + | input Integer B; |
| − | X[i | + | input Integer p1; |
| + | input Integer p2; | ||
| + | output Real G[N,N]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:B loop | ||
| + | for j in 1:B loop | ||
| + | G[i,j]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | G[2*p1,2*p1]:=Y[2,2]; | ||
| + | G[2*p1-1,2*p1-1]:=Y[1,1]; | ||
| + | G[2*p1,2*p1-1]:=Y[2,1]; | ||
| + | G[2*p1-1,2*p1]:=Y[1,2]; | ||
| + | |||
| + | G[2*p2,2*p2]:=Y[4,4]; | ||
| + | G[2*p2-1,2*p2-1]:=Y[3,3]; | ||
| + | G[2*p2,2*p2-1]:=Y[4,3]; | ||
| + | G[2*p2-1,2*p2]:=Y[3,4]; | ||
| + | |||
| + | G[2*p2,2*p1]:=Y[4,2]; | ||
| + | G[2*p2-1,2*p1-1]:=Y[3,1]; | ||
| + | G[2*p2,2*p1-1]:=Y[4,1]; | ||
| + | G[2*p2-1,2*p1]:=Y[3,2]; | ||
| + | |||
| + | G[2*p1,2*p2]:=Y[2,4]; | ||
| + | G[2*p1-1,2*p2-1]:=Y[1,3]; | ||
| + | G[2*p1,2*p2-1]:=Y[2,3]; | ||
| + | G[2*p1-1,2*p2]:=Y[1,4]; | ||
| + | |||
| + | end Local_Global; | ||
| + | |||
| + | ====Gauss Jordan==== | ||
| + | function Gauss_Jordan | ||
| + | input Integer N; | ||
| + | input Real A[N,N]; | ||
| + | input Real B[N]; | ||
| + | output Real X[N]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | X:=Modelica.Math.Matrices.solve(A,B); | ||
| + | for i in 1:N loop | ||
| + | if abs(X[i]) <= float_error then | ||
| + | X[i] := 0; | ||
end if; | end if; | ||
end for; | end for; | ||
| − | |||
| − | end | + | end Gauss_Jordan; |
| − | ==== | + | ====Reaction==== |
| − | function | + | function Reaction_Trusses1 |
| − | input Real | + | input Integer N; |
| − | input | + | input Real A[N,N]; |
| − | input | + | input Real B[N,N]; |
| − | + | input Real C[N,N]; | |
| − | output Real | + | Real X[8,1]; |
| + | output Real Sol[8]; | ||
| + | Real float_error = 10e-10; | ||
| − | algorithm | + | algorithm |
| + | X:=A*B-C; | ||
| − | for i in 1: | + | for i in 1:N loop |
| − | for | + | if abs(X[i,1]) <= float_error then |
| − | + | X[i,1] := 0; | |
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | Sol[i]:=X[i,1]; | ||
end for; | end for; | ||
| − | |||
| − | + | end Reaction_Trusses1; | |
| − | + | ||
| − | + | ===Pertemuan Ke-4=== | |
| − | + | ||
| + | ====Quiz: Diagram Class & Flowchart==== | ||
| + | |||
| + | [[File:Yokkk_KUIZ.jpg|700px|thumb|center]] | ||
| + | |||
| + | ====Pr Trusses==== | ||
| + | |||
| + | [[File:Pr Trusses.jpg|700px|thumb|center]] | ||
| + | |||
| + | [[File:Diagram ja.jpg|700px|thumb|center]] | ||
| + | |||
| + | [[File:Rajatugas.jpg|700px|thumb|center]] | ||
| + | |||
| + | [[File:Rajatugas1.jpg|700px|thumb|center]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <youtube width="200" height="100">PIaJ11PMbhM</youtube> | ||
| + | </div> | ||
| + | |||
| + | ===Pertemuan ke-5=== | ||
| + | |||
| + | sebelum kelas dimulai bu faizah memberikan materi pengantar melalui wa grup.Optimasi adalah suatu cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan | ||
| + | |||
| + | Penyelesaian Tugas: | ||
| + | |||
| + | Fungsi yang dipanggil | ||
| + | [[File:King 1.png]] | ||
| − | + | Dilanjutkan dengan membuat model yang akan memanggil fungsi: | |
| − | + | [[File:King.png]] | |
| − | |||
| − | |||
| − | + | Maka akan didapatkan hasil berupa | |
| − | + | [[File:King 2.png]] | |
| − | + | [[File:King 4.png]] | |
| − | |||
| − | + | ====Tugas Besar Metoda Numerik==== | |
| − | + | Tema : Aplikasi Metoda Numerik dalam Optimasi Desain Struktur Rangka Sederhana | |
| − | |||
| − | |||
| − | + | '''Sinopsis Tugas Besar''' | |
| − | + | Dalam tugas besar ini kami diminta untuk mendesain rangka sesuai yang tertera dibawah dengan menggunakan rangka yang optimal dan cost yang minimum | |
| − | + | [[File:Soaltubesy.jpeg]] | |
| − | + | [[File:Soaltubes1.jpeg]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ====Adapun Hal yang Harus Diperhitungkan sebagai Plotting==== | |
| + | *a. Harga material di dapat dari nilai optimum defleksi dan cross section | ||
| + | *b. Material (Elastisitas properti) | ||
| + | *c. Area Cross Section Truss (L profile/truss siku), luas cross section sebagai X | ||
| + | *d. Defleksi sebagai Y | ||
| − | + | ====Metodologi/Alur Penyelesaian==== | |
| − | for i in 1: | + | |
| − | + | Untuk Jenis Material Tetap | |
| − | + | *Mencari data yang diperlukan yang berkaitan dengan material yang dipilih (SS400); yaitu yield strength dan elasticity | |
| − | + | *Mencari data harga besi sesuai dengan material dan dimensi standar | |
| − | end | + | *Mencari nilai harga batang keseluruhan per 6 meter menggunakan curve fitting |
| + | *Menghitung total cost yang dikeluarkan untuk keseluruhan sistem per masing-masing dimensi besi | ||
| + | *Menghitung stress yang terjadi pada tiap dimensi batang | ||
| + | *Menghitung safety factor | ||
| + | *Menghitung perbandingan antara safety factor dengan harga | ||
| + | *Melakukan optimasi dengan menggunakan metode golden section | ||
| + | |||
| + | ====Menggunakan Jenis Material Tetap==== | ||
| + | Saya mendapatkan data dari beberapa sumber : | ||
| + | *http://www.pusatbesibaja.co.id/harga-besi-siku-profil-baja-distributor-pabrik-supplier-agen-jual-toko-produsen/ | ||
| + | *https://www.theworldmaterial.com/jis-g3101-ss400-steel-equivalent-material/ | ||
| + | *http://www.matweb.com/search/DataSheet.aspx?MatGUID=caff8670b59f4e0ca206dc37e25ce051 | ||
| + | |||
| + | Setelah itu, Saya memasukkan daata tersebut ke dalam excel | ||
| + | [[File:Screenshot (1313).png|700px|thumb|center]] | ||
| + | |||
| + | Kemudian,saya mencari koefisien persamaan curve fitting menggunakan algoritma berikut | ||
| + | |||
| + | Curve Fitting | ||
| + | |||
| + | function CurveFitting_MRaja | ||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | end CurveFitting_MRaja; | ||
| + | |||
| + | fungsi panggil | ||
| + | |||
| + | model Panggil_CurveFitting_FittingCost_MRaja | ||
| + | parameter Real X[6]={0.000141, 0.000171, 0.000231, 0.000304,0.000375, | ||
| + | 0.000425}; | ||
| + | parameter Real Y[6]={51760, 65280, 86000, 111000, 141000, 161000}; | ||
| + | Real Coe[3] | ||
| + | equation | ||
| + | Coe=Curve_fitting(X,Y,2) | ||
| + | end Panggil_CurveFitting_FittingCost_MRaja; | ||
| + | |||
| + | Selanjutnya saya mencari nilai stress maksimum yang dapat digunakan untuk mencari harga | ||
| + | |||
| + | [[File:Screenshot (1323).png|700px|thumb|center]] | ||
| + | [[File:Screenshot (1324).png|700px|thumb|center]] | ||
| + | [[File:Screenshot (1325).png|700px|thumb|center]] | ||
| + | [[File:Screenshot (1326).png|700px|thumb|center]] | ||
| + | [[File:Screenshot (1327).png|700px|thumb|center]] | ||
| + | [[File:Screenshot (1328).png|700px|thumb|center]] | ||
| + | [[File:Screenshot (1329).png|700px|thumb|center]] | ||
| + | [[File:TUBESQU.jpeg|700px|thumb|center]] | ||
| + | |||
| + | berdasarkan hasil simulate diatas maka kriteria dimensi material yang optimum adalah 0.003 m x 0.003 m dengan ketebalan 0.0005 m | ||
| + | |||
| + | [[File:Screenshot (1331).png|700px|thumb|center]] | ||
| + | |||
| + | dengan menggunakan curve fitting, saya membuat fungsi denga X = elastisitas material dan Y = harga | ||
| + | |||
| + | [[File:Screenshot (1333).png|700px|thumb|center]] | ||
| + | |||
| + | dan didapat koefisien sebagai berikut | ||
| + | [[File:TUBES.jpeg|700px|thumb|center]] | ||
| + | |||
| + | dari ketiga koefisien tersebut saya memasukkannya ke program excel | ||
| + | [[File:TUBES2.jpeg|700px|thumb|center]] | ||
| − | + | Selanjutnya dengan menggunakan metode golden section saya melakukan optimasi dengan coding yang sama namun mengganti nilai xd = elastisitas dan yd = Ratio (Safety/Cost) | |
| − | + | [[File:Screenshot (1337).png|700px|thumb|center]] | |
| + | [[File:Screenshot (1338).png|700px|thumb|center]] | ||
| − | + | Sehingga didapat nilai optimum | |
| − | + | [[File:TUBESQ.png|700px|thumb|center]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Kesimpulan''' | |
| − | + | Kondisi optimal untuk material SS316 yaitu pada luas area 0.000141 m^2 (Dimensi besi 2.5cm x 2.5cm x 3 mm) | |
| − | + | ===UAS=== | |
| − | + | ====soal no.1==== | |
| − | + | [[File:Soal no.1.png]] | |
| − | + | ====soal no.2==== | |
| − | + | [[File:Soal no.2.png]] | |
| + | ====soal no.3==== | ||
| + | [[File:Soal no.3.png]] | ||
| + | ====soal no.4==== | ||
| + | [[File:Yokkk_KUIZ.jpg]] | ||
| + | [[File:Diagram ja.jpg]] | ||
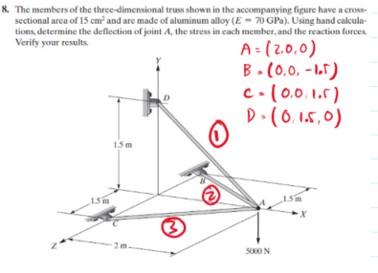
| + | ====soal no.5==== | ||
| + | [[File:Soal no.5.jpg]] | ||
| − | + | ====soal no.7==== | |
| − | + | [[File:7.1.png]] | |
| − | + | [[File:7.2.png]] | |
| + | [[File:7.3.png]] | ||
| − | + | ==Terima Kasih Pak Dai Untuk 1 Semesternya== | |
Latest revision as of 17:29, 14 January 2021
Biodata
Nama : M. Raja
NPM : 1906379106
TTL : Payakumbuh, 24 Juli 2001
Tempat Tinggal: Payakumbuh, Sumatera Barat
Golongan Darah: B
Hobi : Travelling
Saat ini, saya adalah mahasiswa semester 3 program studi Teknik Mesin Universitas Indonesia. Saya memilih jurusan ini karena saya terinspirasi oleh bapak B.J. Habibie dan juga disarankan oleh saudara kandung saya untuk memilih jurusan ini. Saya sangat bersyukur bisa menjadi mahasiswa Teknik Mesin Universitas Indonesia, karena menurut saya tempat ini adalah tempat yang terbaik yang diizinkan Allah SWT untuk saya berkembang. Dengan ini, saya berharap Semoga ilmu yang saya pelajari di perkuliahan ini dapat saya terapkan untuk kebaikan orang banyak di suatu saat nanti dan menjadi ladang amal untuk diri saya pribadi.
Contents
Metode Numerik
Berdasarkan pemahaman saya, metode numerik adalah suatu cara dalam penyelesaian permasalahan yang menggunakan formulasi secara matematis dengan menggunakan operasi hitungan aritmatika dengan proses tambah, kurang, kali, dan bagi. Pada setengah semester pertama di mata kuliah metode numerik, kami dipandu oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Beberapa topik yang dibahas yaitu:
1. Sistem Persamaan
2. Pseudocode
3. Turunan Numerik
4. Metode Newton Rhapson, Secant, dan Bisection
5. Interpolasi
6. Regresi Linear
Setelah UTS, setengah semester terkahir, perkuliahan Metode Numerik diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara
Pertemuan 1 (11 November 2020)
Pada pertemuan minggu ini, dipaparkan tujuan-tujuan pembelajaran metode numerik, yaitu: Tujuan: 1.Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik, seperti: Persamaan aljabar, algorithma, persamaan diferensial parsial, dll.
2.Mengerti aplikasi metode numerik.
3.Mampu menerapkan metode numerik dallam persoalan teknik.
4.Mendapat nilai tambah sehingga kita menjadi orang yang lebih beradab.
Tugas Minggu 1
Kami diminta mempelajari Open Modelica, yaitu sebuah aplikasi untuk membuat modelling dan simulasi. Untuk mempelejari aplikasi tersebut, saya menonton beberapa video dari youtube:
Dengan mempelajari beberapa tutorial dasar penggunaan OpenModelica, saya mencoba untuk mengaplikasikannya ke persamaan GLBB, videonya sebagai berikut:
Pertemuan 2 (18 November 2020)
Dalam metode numerik, segalanya berpusat dalam perhitungan. Dalam proses perhitungan sendiri merupakan suatu seni untuk menyusun algoritma yang cepat, efisien, dan menghasilkan output yang akurat.
- Dalam dunia Teknik, faktor cepat dan akurat memegang peranan yang penting dalam penggunaan di lapangan. Sebagai seorang calon Engineer, kita memerlukan suatu sistem yang dapat memenuhi dua aspek penting sebelumnya untuk menyelesaikan permasalahan secara efisien baik di lapangan maupun dalam proses perancangan.
- Bahasa mesin yang cepat untuk mengeluarkan nilai outputnya adalah bahasa Fortran dan C. Namun beliau lebih memilih untuk menggunakan bahasa Modelica dalam mata kuliah Metode Numerik karena beberapa alasan:
1. Modelica adalah bahasa pemodelan yang cukup mudah dipahami.
2. Modelica dapat mengeluarkan hasil hitungan yang cepat karena menggunakan bahasa pemrograman C.
3. Modelica merupakan suatu bahasa yang open source, sehingga gratis dan mudah diakses oleh semua orang, serta memiliki komunitas pengguna yang cukup banyak.
Dalam menggunakan OpenModelica, untuk melakukan suatu perhitungan, maka variabel haruslah didefinisikan.
- Apabila variabel tersebut memiliki nilai; maka nilai tersebut haruslah ditulis dengan menggunakan parameter Real variabel=nilai
- Apabila variabel tersebut merupakan persamaan atau sesuatu yang ingin kita cari, maka variabel tersebut harus dituliskan dalam equation.
Tugas Minggu 2
Kami diminta untuk mengaplikasikan Open Modelica lebih lanjut dan saya mencoba mengaplikasikannya untuk mencari solusi dari sebuah matrix menggunakan open modelica ini dan membandingkannya dengan hasil yang didapat secara manual, berikut adalah video tugas tersebut:
Pertemuan ke-3
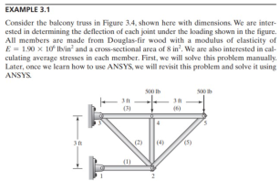
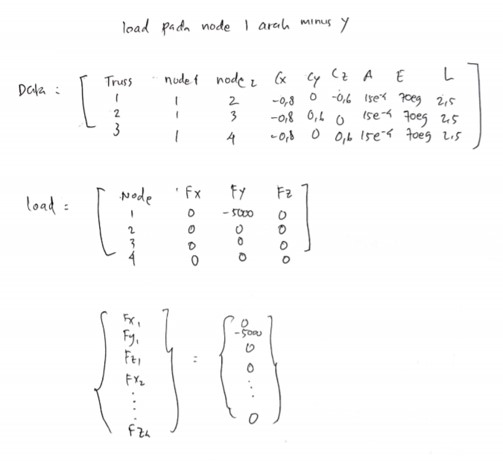
Tugas Minggu 3
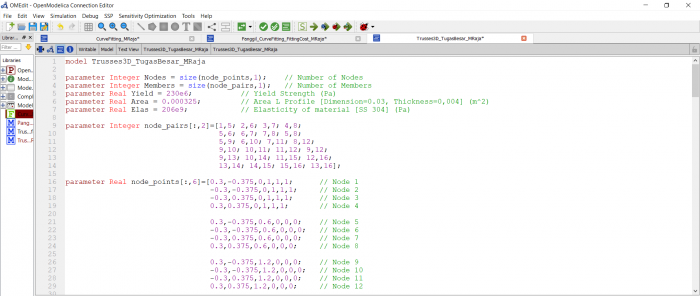
model Trusses_PR
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
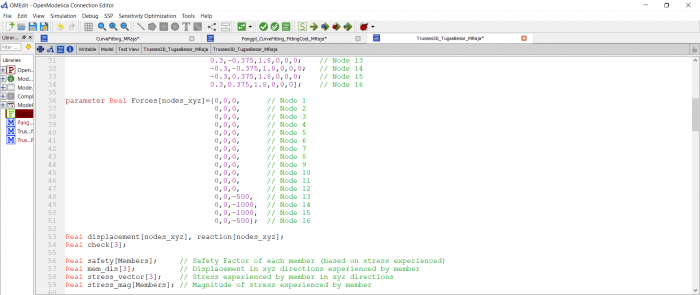
Real XMat[N,1];
//boundary coundition Integer b1=1; Integer b2=3;
//truss 1 parameter Real X1=0; //degree between truss Real k1=A*E/36; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N];
//truss 2 parameter Real X2=135; //degree between truss Real k2=A*E/50.912; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N];
//truss 3 parameter Real X3=0; //degree between truss Real k3=A*E/36; Real K3[4,4]; //stiffness matrice Integer p3a=3; Integer p3b=4; Real G3[N,N];
//truss 4 parameter Real X4=90; //degree between truss Real k4=A*E/36; Real K4[4,4]; //stiffness matrice Integer p4a=2; Integer p4b=4; Real G4[N,N];
//truss 5 parameter Real X5=45; //degree between truss Real k5=A*E/50.912; Real K5[4,4]; //stiffness matrice Integer p5a=2; Integer p5b=5; Real G5[N,N];
//truss 6 parameter Real X6=0; //degree between truss Real k6=A*E/36; Real K6[4,4]; //stiffness matrice Integer p6a=4; Integer p6b=5; Real G6[N,N];
/* for each truss, please ensure pXa is lower then pXb (X represents truss element number) */
algorithm
//creating global matrice K1:=Kekakuan_Matrix(X1); G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Kekakuan_Matrix(X2); G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Kekakuan_Matrix(X3); G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Kekakuan_Matrix(X4); G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Kekakuan_Matrix(X5); G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Kekakuan_Matrix(X6); G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6; Ginitial:=G;
//implementing boundary condition for i in 1:N loop G[2*b1-1,i]:=0; G[2*b1,i]:=0; G[2*b2-1,i]:=0; G[2*b2,i]:=0; end for;
G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1;
//solving displacement Sol:=Gauss_Jordan(N,G,X);
//solving reaction force SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Trusses1(N,Ginitial,SolMat,XMat);
end Trusses_PR;
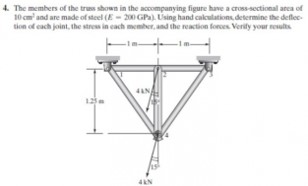
class Trusses
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m^2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global displacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition Integer b1=1; Integer b2=3;
//truss 1 parameter Real X1=0; //degree between truss Real k1=A*E/1; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N];
//truss 2 parameter Real X2=0; //degree between truss Real k2=A*E/1; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N];
//truss 3 parameter Real X3=90; //degree between truss Real k3=A*E/1.25; Real K3[4,4]; //stiffness matrice Integer p3a=2; Integer p3b=4; Real G3[N,N];
//truss 4 parameter Real X4=90+38.6598; //degree between truss Real k4=A*E/1.6; Real K4[4,4]; //stiffness matrice Integer p4a=1; Integer p4b=4; Real G4[N,N];
//truss 5 parameter Real X5=90-38.6598; //degree between truss Real k5=A*E/1.6; Real K5[4,4]; //stiffness matrice Integer p5a=3; Integer p5b=4; Real G5[N,N];
/* for each truss, please ensure pXa is lower then pXb (X represents truss element number) */
algorithm
//creating global matrice K1:=Kekakuan_Matrix(X1); G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Kekakuan_Matrix(X2); G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Kekakuan_Matrix(X3); G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Kekakuan_Matrix(X4); G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Kekakuan_Matrix(X5); G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5; Ginitial:=G;
//implementing boundary condition for i in 1:N loop G[2*b1-1,i]:=0; G[2*b1,i]:=0; G[2*b2-1,i]:=0; G[2*b2,i]:=0; end for;
G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1;
//solving displacement Sol:=Gauss_Jordan(N,G,X);
//solving reaction force SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Trusses1(N,Ginitial,SolMat,XMat);
end Trusses;
Fungsi Panggil
function Kekakuan_Matrix input Real A; Real Y; output Real X[4,4]; Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi; X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),- (Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,- Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2; -(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y), (Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),- (Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y), (Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Kekakuan_Matrix;
Function
function Local_Global input Real Y[4,4]; input Integer B; input Integer p1; input Integer p2; output Real G[N,N];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2]; G[2*p1-1,2*p1-1]:=Y[1,1]; G[2*p1,2*p1-1]:=Y[2,1]; G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4]; G[2*p2-1,2*p2-1]:=Y[3,3]; G[2*p2,2*p2-1]:=Y[4,3]; G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2]; G[2*p2-1,2*p1-1]:=Y[3,1]; G[2*p2,2*p1-1]:=Y[4,1]; G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4]; G[2*p1-1,2*p2-1]:=Y[1,3]; G[2*p1,2*p2-1]:=Y[2,3]; G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
Gauss Jordan
function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10;
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan;
Reaction
function Reaction_Trusses1 input Integer N; input Real A[N,N]; input Real B[N,N]; input Real C[N,N]; Real X[8,1]; output Real Sol[8]; Real float_error = 10e-10;
algorithm X:=A*B-C;
for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for;
for i in 1:N loop Sol[i]:=X[i,1]; end for;
end Reaction_Trusses1;
Pertemuan Ke-4
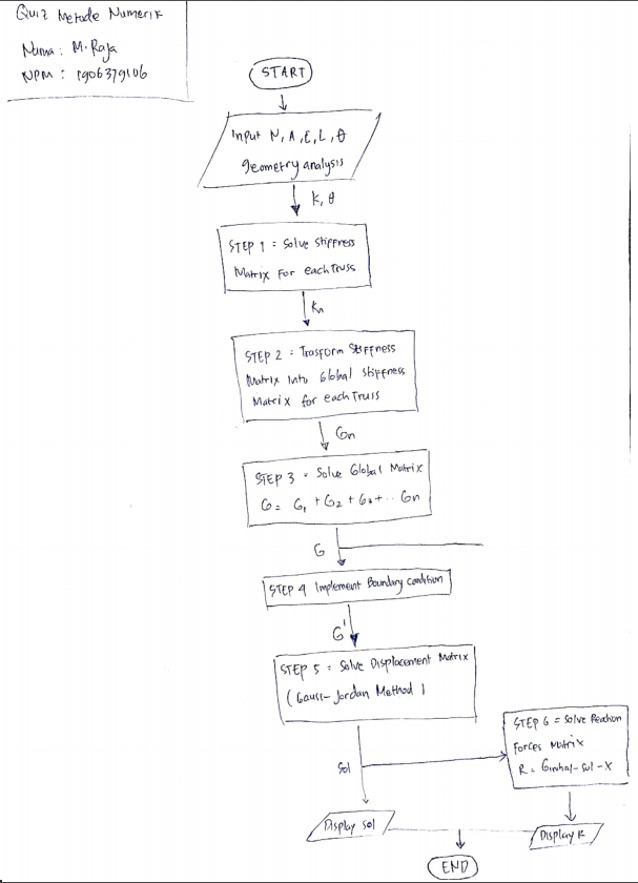
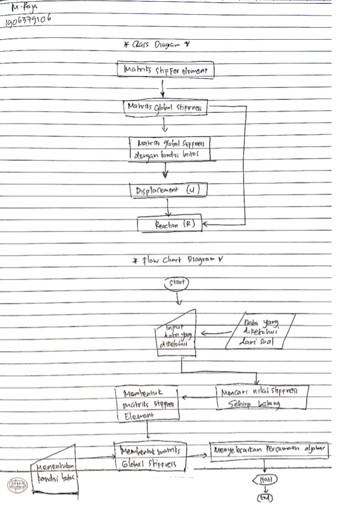
Quiz: Diagram Class & Flowchart
Pr Trusses
Pertemuan ke-5
sebelum kelas dimulai bu faizah memberikan materi pengantar melalui wa grup.Optimasi adalah suatu cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan
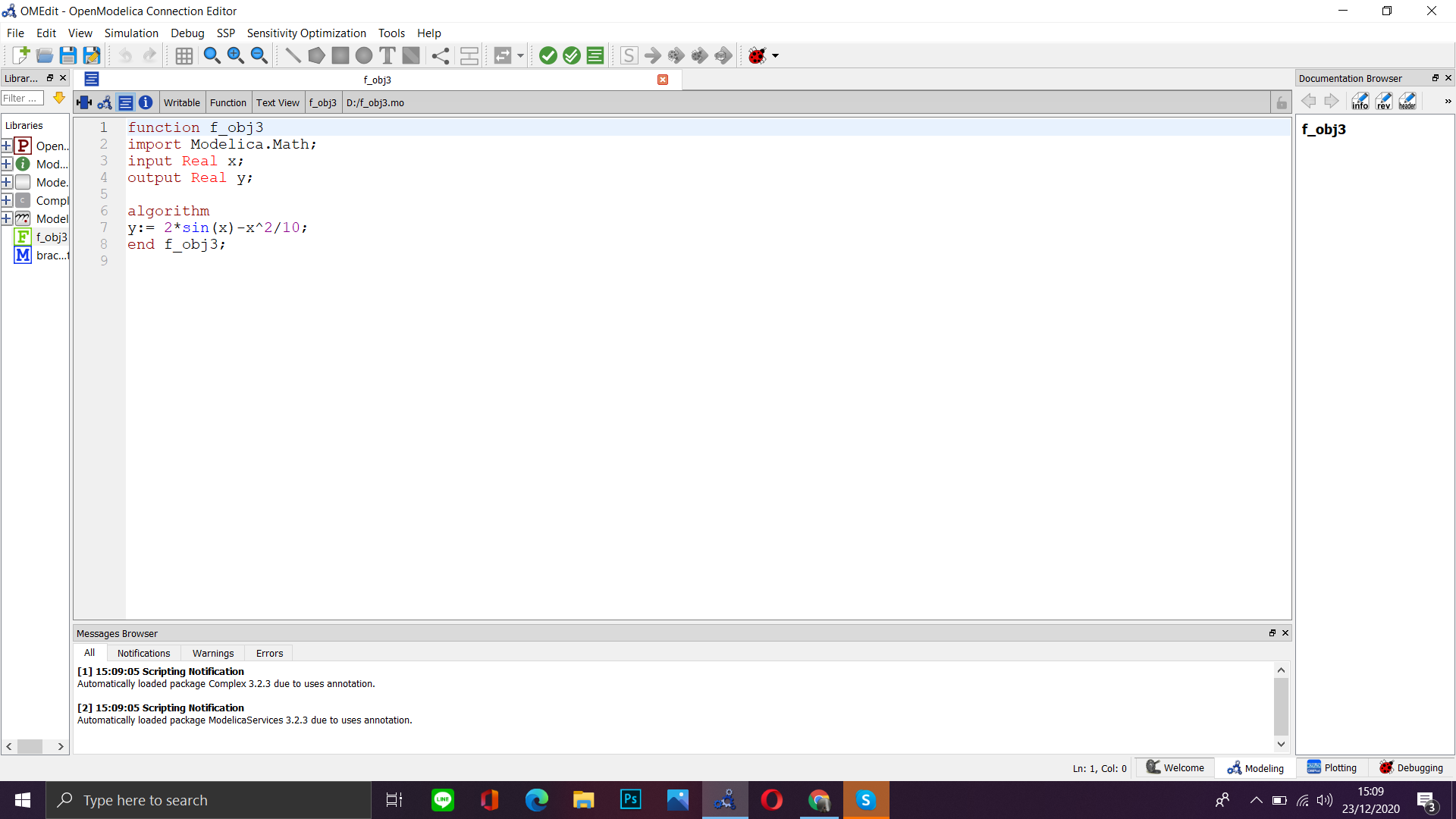
Penyelesaian Tugas:
Dilanjutkan dengan membuat model yang akan memanggil fungsi:
Maka akan didapatkan hasil berupa
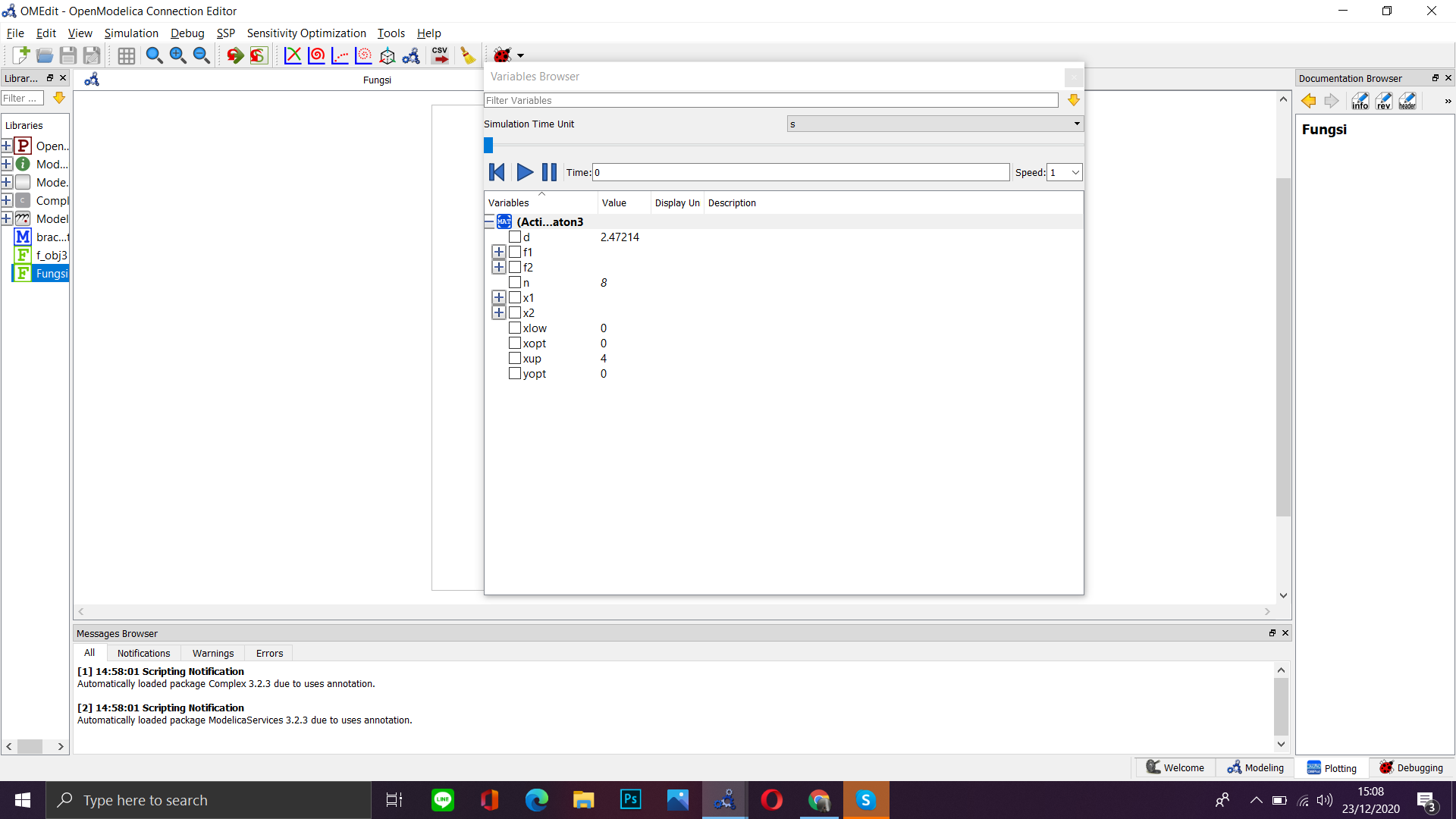
Tugas Besar Metoda Numerik
Tema : Aplikasi Metoda Numerik dalam Optimasi Desain Struktur Rangka Sederhana
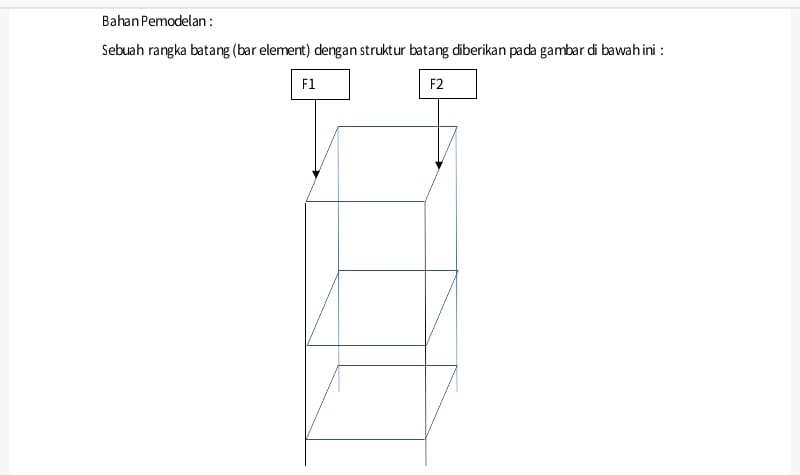
Sinopsis Tugas Besar
Dalam tugas besar ini kami diminta untuk mendesain rangka sesuai yang tertera dibawah dengan menggunakan rangka yang optimal dan cost yang minimum
Adapun Hal yang Harus Diperhitungkan sebagai Plotting
- a. Harga material di dapat dari nilai optimum defleksi dan cross section
- b. Material (Elastisitas properti)
- c. Area Cross Section Truss (L profile/truss siku), luas cross section sebagai X
- d. Defleksi sebagai Y
Metodologi/Alur Penyelesaian
Untuk Jenis Material Tetap
- Mencari data yang diperlukan yang berkaitan dengan material yang dipilih (SS400); yaitu yield strength dan elasticity
- Mencari data harga besi sesuai dengan material dan dimensi standar
- Mencari nilai harga batang keseluruhan per 6 meter menggunakan curve fitting
- Menghitung total cost yang dikeluarkan untuk keseluruhan sistem per masing-masing dimensi besi
- Menghitung stress yang terjadi pada tiap dimensi batang
- Menghitung safety factor
- Menghitung perbandingan antara safety factor dengan harga
- Melakukan optimasi dengan menggunakan metode golden section
Menggunakan Jenis Material Tetap
Saya mendapatkan data dari beberapa sumber :
- http://www.pusatbesibaja.co.id/harga-besi-siku-profil-baja-distributor-pabrik-supplier-agen-jual-toko-produsen/
- https://www.theworldmaterial.com/jis-g3101-ss400-steel-equivalent-material/
- http://www.matweb.com/search/DataSheet.aspx?MatGUID=caff8670b59f4e0ca206dc37e25ce051
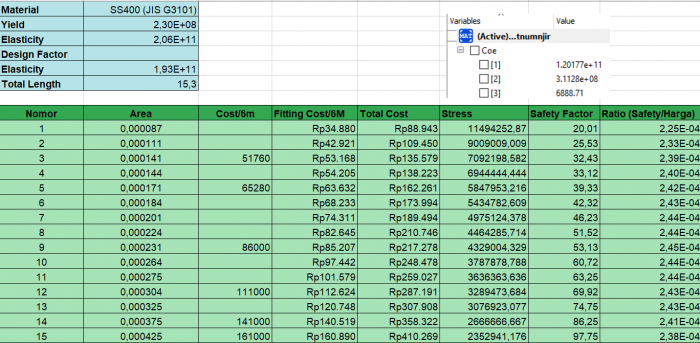
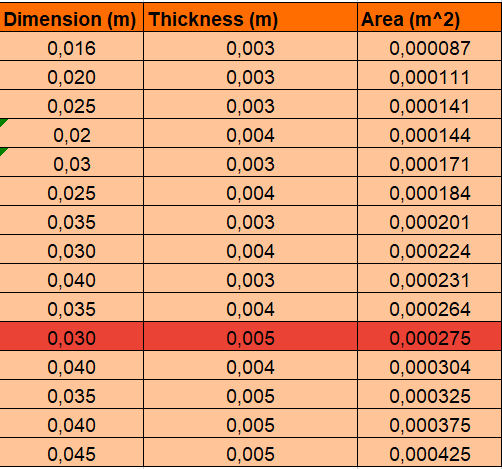
Setelah itu, Saya memasukkan daata tersebut ke dalam excel
Kemudian,saya mencari koefisien persamaan curve fitting menggunakan algoritma berikut
Curve Fitting
function CurveFitting_MRaja input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end CurveFitting_MRaja;
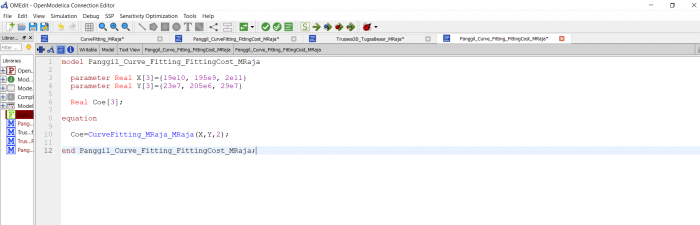
fungsi panggil
model Panggil_CurveFitting_FittingCost_MRaja
parameter Real X[6]={0.000141, 0.000171, 0.000231, 0.000304,0.000375,
0.000425};
parameter Real Y[6]={51760, 65280, 86000, 111000, 141000, 161000};
Real Coe[3]
equation
Coe=Curve_fitting(X,Y,2)
end Panggil_CurveFitting_FittingCost_MRaja;
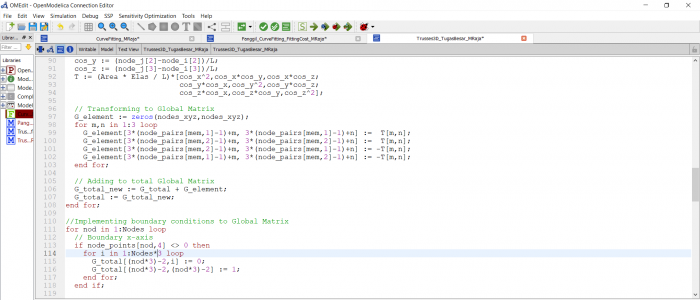
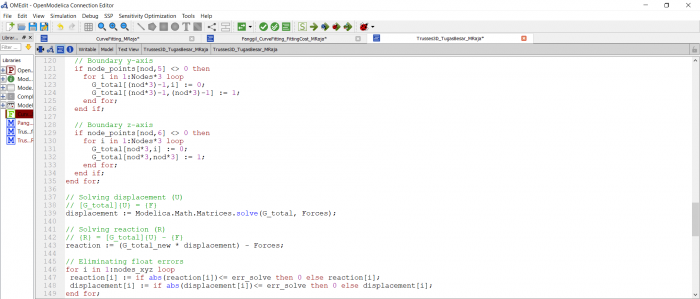
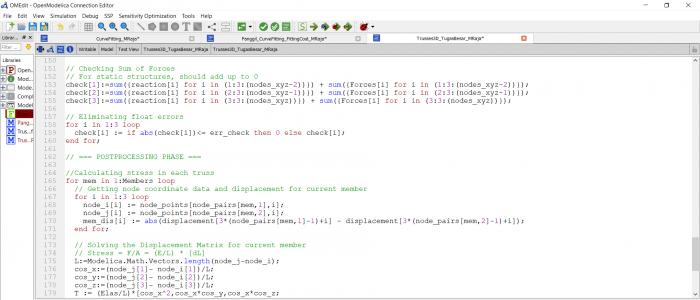
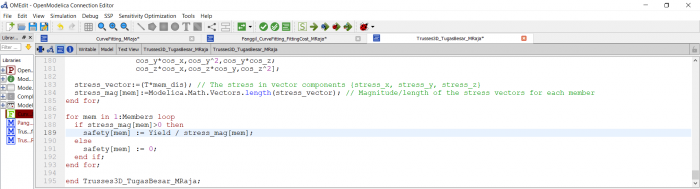
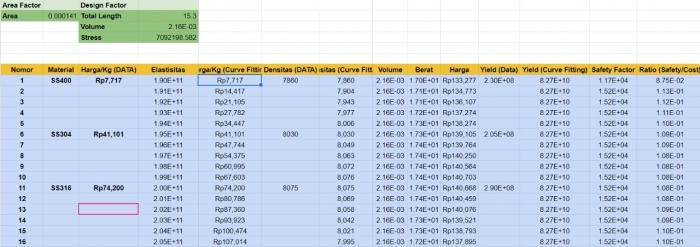
Selanjutnya saya mencari nilai stress maksimum yang dapat digunakan untuk mencari harga
berdasarkan hasil simulate diatas maka kriteria dimensi material yang optimum adalah 0.003 m x 0.003 m dengan ketebalan 0.0005 m
dengan menggunakan curve fitting, saya membuat fungsi denga X = elastisitas material dan Y = harga
dan didapat koefisien sebagai berikut
dari ketiga koefisien tersebut saya memasukkannya ke program excel
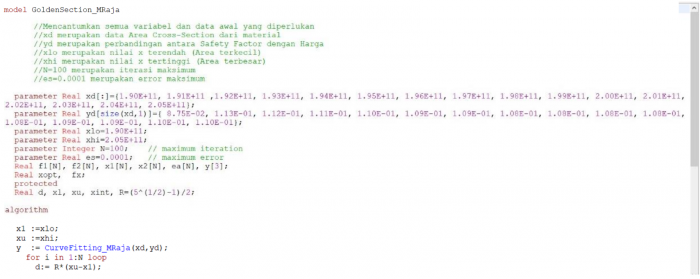
Selanjutnya dengan menggunakan metode golden section saya melakukan optimasi dengan coding yang sama namun mengganti nilai xd = elastisitas dan yd = Ratio (Safety/Cost)
Sehingga didapat nilai optimum
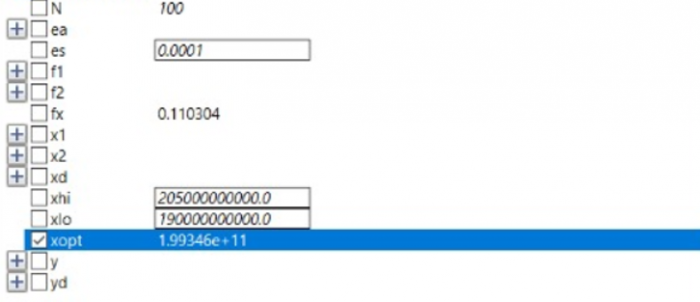
Kesimpulan Kondisi optimal untuk material SS316 yaitu pada luas area 0.000141 m^2 (Dimensi besi 2.5cm x 2.5cm x 3 mm)