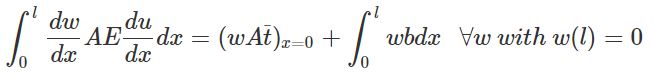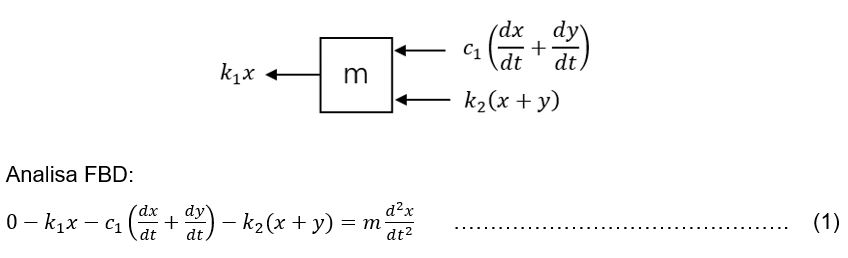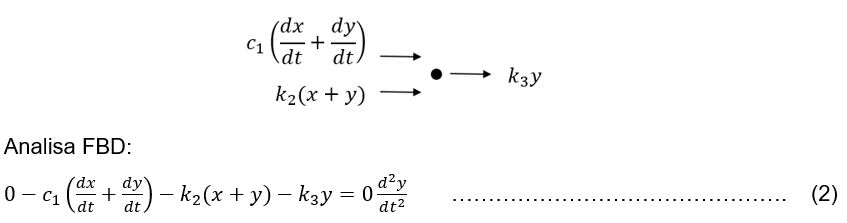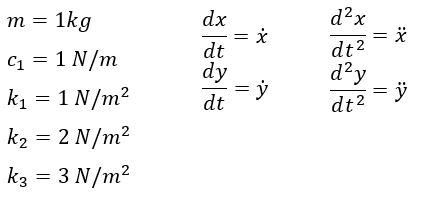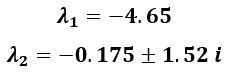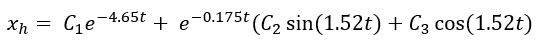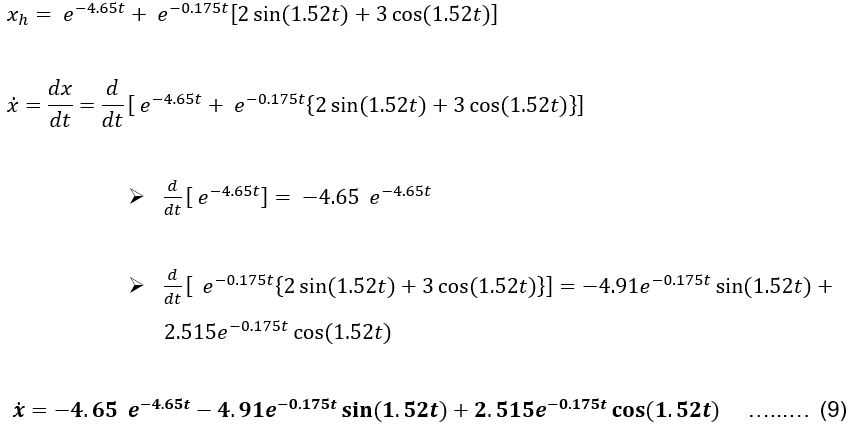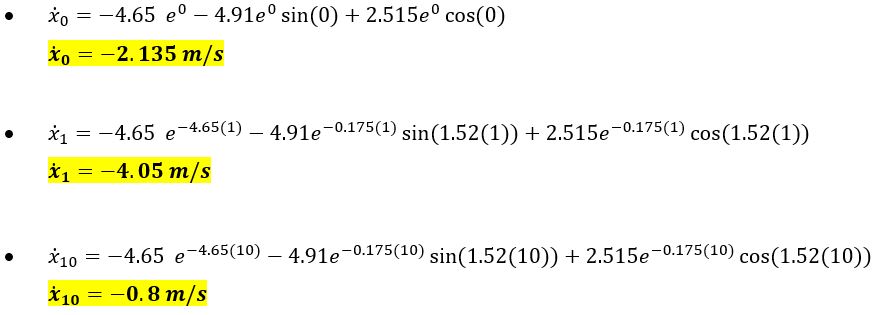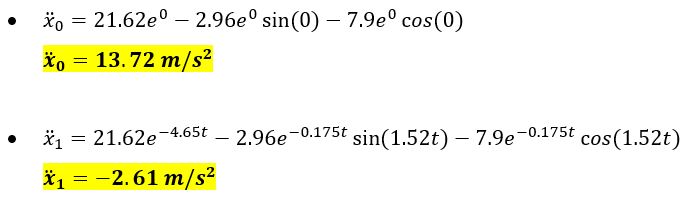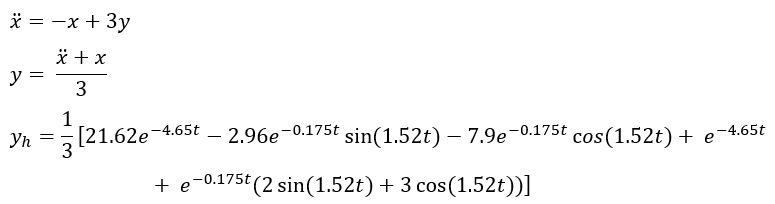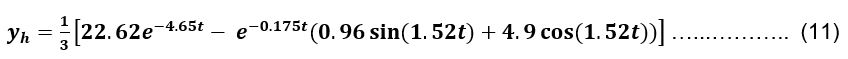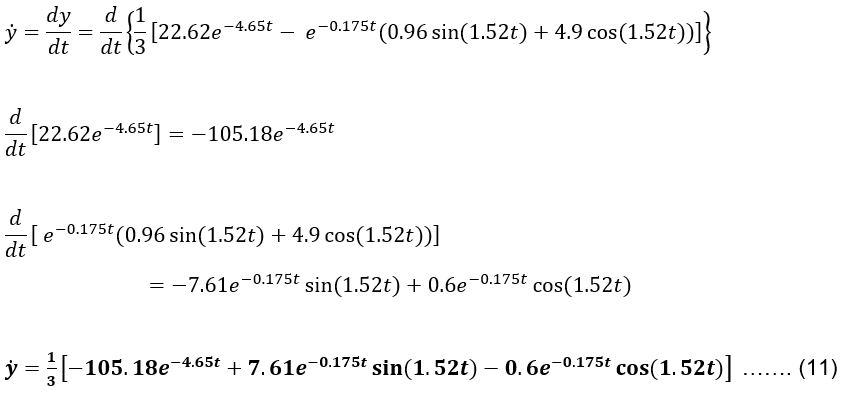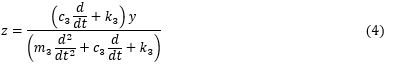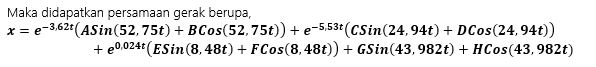Difference between revisions of "Evi Elisa Ambarita"
(→9 Maret 2020) |
|||
| (56 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Pendahuluan Komputasi Teknik == | ==Pendahuluan Komputasi Teknik == | ||
| Line 41: | Line 15: | ||
3. Memiliki pengenalan diri yang lebih tentang muhasabah, skill, value, dsb. | 3. Memiliki pengenalan diri yang lebih tentang muhasabah, skill, value, dsb. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Quiz== | ==Quiz== | ||
| Line 93: | Line 46: | ||
source: https: //www. simscale.com/docs/content/simwiki/fea/whatisfea.html | source: https: //www. simscale.com/docs/content/simwiki/fea/whatisfea.html | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Optimasi Kebutuhan Energi Manusia== | ==Optimasi Kebutuhan Energi Manusia== | ||
| Line 163: | Line 109: | ||
==UTS== | ==UTS== | ||
| + | |||
| + | ===Video presentasi=== | ||
| + | |||
| + | Video presentasi hasil belajar terkait pengetahuan (konsep/teori) dan keterampilan (menggunakan komputasi teknik) | ||
| + | |||
| + | [[File:UTS_Komtek_Evi.mp4|500px]] | ||
| + | |||
| + | |||
| + | ===Laporan tugas optimasi=== | ||
| + | |||
| + | Laporan hasil tugas optimasi kebutuhan energi manusia. | ||
| + | |||
| + | Berdasarkan hasil diskusi kelas pada ( http://air.eng.ui.ac.id/index.php?title=Optimasi_Sistem_Energi_pada_Manusia ) ini, berikut optimasi kebutuhan energi saya pribadi selama seminggu (March 16th - 22nd), | ||
| + | |||
| + | Kebutuhan kalori yang saya butuhkan dalam 1 minggu: | ||
| + | |||
| + | [[File:Evi16.JPG|500px]] | ||
| + | [[File:Evi17.JPG|500px]] | ||
| + | [[File:Evi18.JPG|500px]] | ||
| + | [[File:Evi19.JPG|500px]] | ||
| + | [[File:Evi20.JPG|500px]] | ||
| + | [[File:Evi21.JPG|500px]] | ||
| + | [[File:Evi22.JPG|500px]] | ||
| + | |||
| + | Kebutuhan listrik yang saya butuhkan dalam 1 minggu: | ||
| + | |||
| + | [[File:evi23.JPG|1000px]] | ||
| + | |||
| + | Sehingga diperoleh total energi dan total biaya yang saya butuhkan dalam seminggu: | ||
| + | |||
| + | [[File:Evi30.JPG]] | ||
| + | |||
| + | Dan menghasilkan grafik sebagai berikut: | ||
| + | |||
| + | [[File:Evi33.JPG]] | ||
| + | |||
| + | |||
| + | ==Quiz Oscillating dynamic system== | ||
| + | |||
| + | Memverifikasi sebuah sistem dinamik berosilasi tanpa gesekan (fig. 4.15) dengan menggunakan metode numerik dan metode analitik. Selain itu, terdapat 2 metode numerik yang akan digunakan, yakni standard numerical solution (persamaan 4.47 dan 4.48) dan a magic fix of a numerical method (persamaan 4.49 dan 4.50). | ||
| + | |||
| + | [[File:Osilasievi1.JPG]] | ||
| + | |||
| + | Gambar diatas menjelaskan suatu benda dengan massa m melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan. Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) body (penampang m) kembali dan bekerja "melawan" gerakan, misalkan x (t) adalah posisi body pada sumbu x, dimana body bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (mis., Tidak ada gesekan). Hukum kedua Newton menyatakan F=ma kemudian memiliki F=-kx dan a=x", | ||
| + | |||
| + | -kx = mx" (4.41) | ||
| + | |||
| + | sehingga dapat dituliskan | ||
| + | |||
| + | x" + ω^2 x = 0 (4.42) | ||
| + | |||
| + | Persamaan (4.42) adalah persamaan diferensial orde kedua, dan oleh karena itu kita memerlukan dua kondisi awal, satu pada posisi x(0) dan satu pada kecepatan x’(0). | ||
| + | |||
| + | x (0) = 1,5 dan x’(0) = 0 | ||
| + | |||
| + | Untuk mengendalikan turunan orde dua menggunakan metode numerik, cara yang dapat kita tuliskan pada persamaan 4.42 sebagai sebuah sistem orde pertama dari 2 persamaan turunan. Kita memperkenalkan u=x dan v=x'=u' sebagai 2 fungsi baru yang tidak diketahui. Dua persamaan yang sesuai muncul dari definisi v=u' dan persamaan asal (4.42): | ||
| + | |||
| + | u' = v (4.43) | ||
| + | |||
| + | v' = -ω²u (4.44) | ||
| + | |||
| + | maka u"=v' untuk menghilangkan turunan orde kedua dari hukum kedua newton. | ||
| + | |||
| + | Dengan menggunakan metode numerik pertama, yakni standard numerical solution dengan persamaan-persamaan berikut: | ||
| + | |||
| + | u^(n+1) = u^n + ∆t v^n (4.47) | ||
| + | |||
| + | v^(n+1) = v^n - ∆t ω^2 u^n (4.48) | ||
| + | |||
| + | Selain itu, terdapat juga metode numerik kedua yang anggap lebih akurat, disebut a magic fix of the numerical method dengan mengganti u^n untuk persamaan kedua menjadi u^(n+1) dari persamaan pertama, sehingga: | ||
| + | |||
| + | u^(n+1) = u^n + ∆t v^n (4.49) | ||
| + | |||
| + | v^(n+1) = v^n - ∆t ω^2 u^(n+1) (4.50) | ||
| + | |||
| + | dimana diketahui ω = 2,5 rad/s dan ∆t = 0,05 s, maka dilakukan perhitungan sebagai berikut. | ||
| + | <gallery mode="slideshow"> | ||
| + | File:Osilasievi6.JPG | ||
| + | File:Osilasievi7.JPG | ||
| + | File:Osilasievi8.JPG | ||
| + | File:Osilasievi9.JPG | ||
| + | File:Osilasievi10.JPG | ||
| + | File:Osilasievi11.JPG | ||
| + | File:Osilasievi12.JPG | ||
| + | File:Osilasievi13.JPG | ||
| + | File:Osilasievi14.JPG | ||
| + | </gallery> | ||
| + | |||
| + | Selanjutnya dilakukan verifikasi antara setiap metode numerik diatas terhadap metode analitik, dimana persamaan-persamaan untuk metode analitik adalah sebagai berikut: | ||
| + | |||
| + | u = x cos ωt | ||
| + | |||
| + | v = -x ω cos ωt | ||
| + | |||
| + | yang perhitungan detail nya dapat juga dilihat pada lampiran (ms.excel). | ||
| + | |||
| + | Sehingga diperoleh hasil yang merupakan grafik sebagai berikut: | ||
| + | |||
| + | |||
| + | [[File:Osilasievi2.JPG]] | ||
| + | |||
| + | [[File:Osilasievi3.JPG]] | ||
| + | |||
| + | |||
| + | Dari kedua grafik diatas dapat dilihat jelas bahwa metode numerik yang standard dengan menggunakan persamaan 4.47 dan 4.48 jauh dari kata akurat, dikarenakan hasil yang didapat dari metode ini (grafik biru) sangat berbeda dengan hasil dari metode analitik (grafik abu-abu). Oleh karena itu, metode numerik yang disebut a magic fix for a numerical method perlu dilakukan, dengan hasil sebagai berikut: | ||
| + | |||
| + | |||
| + | [[File:Osilasievi4.JPG]] | ||
| + | |||
| + | [[File:Osilasievi5.JPG]] | ||
| + | |||
| + | |||
| + | Dari kedua grafik diatas, dapat dilihat bahwa metode numerik ini (grafik kuning) memiliki tingkat keakurasian yang sangat baik dengan pemverifikasian terhadap metode analitik (grafik hijau). Dengan demikian, disimpulkan bahwa a magic fix for a numerical method telah terverifikasi terhadap metode analitik yang mana dapat mewakili metode analitik. untuk menentukan nilai u dan v. | ||
| + | |||
| + | ==Artikel 1, OSCILLATING 1-D DYNAMIC SYSTEM== | ||
| + | |||
| + | ===Pendahuluan=== | ||
| + | |||
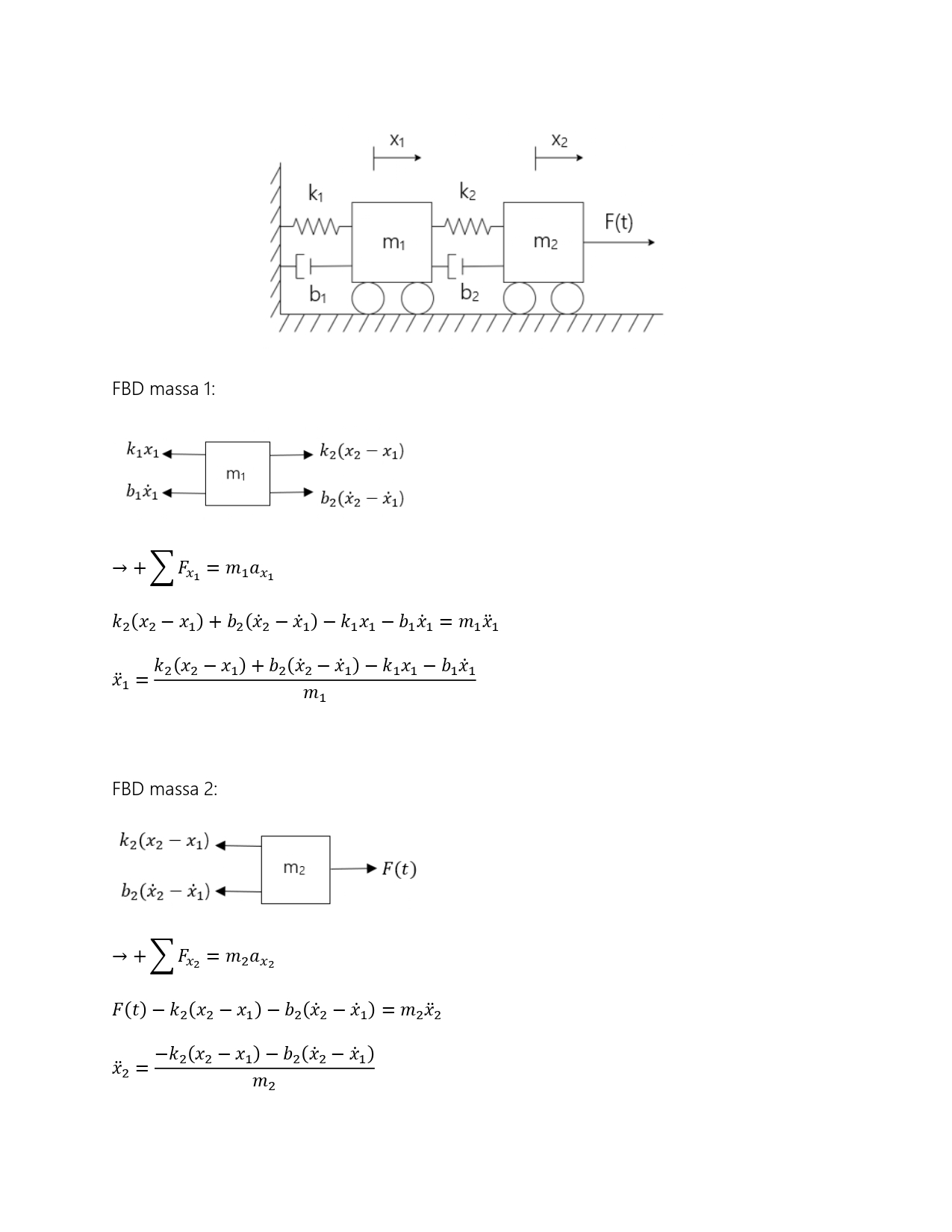
| + | Artikel ini akan membahas penyelesaian permasalahan oscillating 1-D dynamic system pada system damping sesuai gambar di bawah. Pada system di bawah terdapat sebuah massa yang dihubungkan dengan 3 spring, dan 1 dashpot. System tersebut fix pada 2 boundary sisi kiri dan kanan. | ||
| + | |||
| + | [[File:Artikelkomtekevi1.JPG]] | ||
| + | |||
| + | Penyelesaian dari permasalahan tersebut akan dilakukan dengan 3 metode, yang kemudian akan dibandingkan hasil dari perhitungan pada tiap metode tersebut. Metode yang digunakan yaitu: analitikal, numerik, dan simulasi. Pada metode analitikal dilakukan tinjauan gaya aksi – reaksi pada free body diagram (FBD) yang muncul dari eksitasi yang diberikan. Kemudian untuk penyelesaian metode numerik akan dilakukan iterasi dengan bantuan software Microsoft Excel menggunakan Forward Euler. Sedangkan untuk proses simulasi akan dilakukan dengan bantuan software MATLAB. | ||
| + | |||
| + | ===Metode=== | ||
| + | |||
| + | '''Metode Analitik''' | ||
| + | |||
| + | Free Body Diagram (FBD): | ||
| + | |||
| + | • Tinjauan massa: | ||
| + | |||
| + | [[File:Artikelkomtekevi2.JPG]] | ||
| + | |||
| + | • Tinjauan titik: (diantara c1, k2, dan k3) | ||
| + | |||
| + | [[File:Artikelkomtekevi3.JPG]] | ||
| + | |||
| + | ''Diketahui:'' | ||
| + | |||
| + | [[File:Artikelkomtekevi4.JPG]] | ||
| + | |||
| + | Maka persamaan 1 dan 2 dapat dituliskan kembali menjadi; | ||
| + | |||
| + | Persamaan 1 | ||
| + | |||
| + | [[File:Artikelkomtekevi5.JPG]] | ||
| + | |||
| + | Persamaan 2 | ||
| + | |||
| + | [[File:Artikelkomtekevi6.JPG]] | ||
| + | |||
| + | ''Penyelesaian'' | ||
| + | |||
| + | Asumsi | ||
| + | |||
| + | [[File:Artikelkomtekevi7.JPG]] | ||
| + | |||
| + | Karena pada persamaan 5 masih terdapat ̇ y maka subtitusi persamaan 6 ke persamaan 5, sehingga didapatkan nilai ̇ z sebagai berikut; | ||
| + | |||
| + | [[File:Artikelkomtekevi8.JPG]] | ||
| + | |||
| + | Penyelesaian menggunakan matrix; | ||
| + | |||
| + | [[File:Artikelkomtekevi9.JPG]] | ||
| + | |||
| + | Maka didapatkan nilai λ sebesar | ||
| + | |||
| + | [[File:Artikelkomtekevi10.JPG]] | ||
| + | |||
| + | Sehingga didapatkan persamaan | ||
| + | |||
| + | [[File:Artikelkomtekevi11.JPG]] | ||
| + | |||
| + | Jika diasumsikan nilai C1,C2,dan C3 adalah 1, 2 dan 3 maka; | ||
| + | |||
| + | [[File:Artikelkomtekevi12.JPG]] | ||
| + | |||
| + | Nilai x untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi13.JPG]] | ||
| + | |||
| + | Mencari nilai yh dengan mensubtitusi nilai xh ke dalam persamaan ̇ z=-x+3y, di mana nilai ̇ z = ̈ x. | ||
| + | |||
| + | Mencari nilai ̇x; | ||
| + | |||
| + | [[File:Artikelkomtekevi14.JPG]] | ||
| + | |||
| + | Nilai ̇ x untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi15.JPG]] | ||
| + | |||
| + | Mencari nilai ̈ x; | ||
| + | |||
| + | [[File:Artikelkomtekevi16.JPG]] | ||
| + | |||
| + | Persamaan ̈ x di atas dapat disederhanakan menjadi; | ||
| + | |||
| + | [[File:Artikelkomtekevi17.JPG]] | ||
| + | |||
| + | Nilai ̈ x untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi18.JPG]] | ||
| + | |||
| + | Mencari nilai y; | ||
| + | |||
| + | [[File:Artikelkomtekevi19.JPG]] | ||
| + | |||
| + | Persamaan yh dapat disederhanakan menjadi; | ||
| + | |||
| + | [[File:Artikelkomtekevi20.JPG]] | ||
| + | |||
| + | Nilai y untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi21.JPG]] | ||
| + | |||
| + | Mencari nilai ̇ y; | ||
| + | |||
| + | [[File:Artikelkomtekevi22.JPG]] | ||
| + | |||
| + | Nilai ̇ y ketika t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | [[File:Artikelkomtekevi23.JPG]] | ||
| + | |||
| + | |||
| + | '''Metode Numerik''' | ||
| + | |||
| + | Metode ini dilakukan dengan menggunakan software Microsoft Excel. Parameter input yang harus diketahui yaitu x pada t = 0 s, y pada t = 0 s, dan selisih penambahan waktu (∆t). Parameter input x dan y ini dapat juga disebut dengan initial condition. Lalu kemudian dilakukan iterasi sesuai dengan ∆t sampai waktu yang ditentukan. Nilai parameter input tersebut didapat dengan cara analitis seperti sudah disebut di atas, yaitu x((t=0))=4 m; y((t=0))=5.9 m; dan selisih waktu ∆t=0.1 second. | ||
| + | |||
| + | Seperti sudah disebutkan sebelumnya bahwa penyelesaiannya menggunakan Forward Euler, yaitu sebagai berikut: | ||
| + | |||
| + | [[File:Artikelkomtekevi24.JPG]] | ||
| + | |||
| + | '''Simulasi''' | ||
| + | |||
| + | Simulasi dilakukan dengan bantuan software MATLAB. Adapun agar simulasi dapat berjalan, maka perlu diberikan input coding pada software MATLAB yang isinya sebagai berikut. | ||
| + | |||
| + | % Calculates the position, velocity, and acceleration as a function of time | ||
| + | % of a system of carts connected by springs and dashpots. Euler's Method is | ||
| + | % used to solve the equations of motion numerically. | ||
| + | clear all; close all; clc; | ||
| + | tic | ||
| + | |||
| + | % Problem parameters | ||
| + | k1=1; % cart 1 spring constant (N/m) | ||
| + | k2=2; % cart 1 spring constant (N/m) | ||
| + | b1=1; % cart 1 viscous damping coefficient (kg/s) | ||
| + | m1=1; % cart 1 mass (kg) | ||
| + | k3=3; % cart 1 spring constant (N/m) | ||
| + | x10=4; % cart 1 initial position (m) | ||
| + | x20=5.9; % y movement initial position (m) | ||
| + | v10=-2.135; % cart 1 initial velocity (m/s) | ||
| + | v20=-35.36; % cart 2 initial velocity (m/s) | ||
| + | |||
| + | % Set time step stuff | ||
| + | simTime=60; % simulation time (s) | ||
| + | tStep=0.1; % simulation time step | ||
| + | iterations=simTime/tStep; | ||
| + | t=0:iterations; | ||
| + | |||
| + | % Pre-allocate variables for speed and add initial conditions | ||
| + | x1=zeros(iterations,1); | ||
| + | x1(1,:)=x10; | ||
| + | x2=zeros(iterations,1); | ||
| + | x2(1,:)=x20; | ||
| + | v1=zeros(iterations,1); | ||
| + | v1(1,:)=v10; | ||
| + | v2=zeros(iterations,1); | ||
| + | v2(1,:)=v20; | ||
| + | a1=zeros(iterations,1); | ||
| + | a1(1,:)=((0-(k1*x10)-b1*(v10+v20)-k2*(x20+x10))/m1); | ||
| + | |||
| + | % Solve the ODE's with Euler's Method | ||
| + | for n=2:(iterations+1) | ||
| + | x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position | ||
| + | x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position | ||
| + | v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity | ||
| + | v2(n,:)=-(2*x1(n,:)+5*x2(n,:)+v1(n,:)) | ||
| + | % Find cart accelerations | ||
| + | a1(n,:)=((0-k1*x1(n,:))-b1*(v1(n,:)+v2(n,:))-k2*(x2(n,:)+x1(n,:))/m1); | ||
| + | end | ||
| + | |||
| + | % Plot results | ||
| + | subplot(3,1,1) | ||
| + | hold on; | ||
| + | plot(t',x1,'r') | ||
| + | plot(t',x2,'m') | ||
| + | ylabel('Position (m)') | ||
| + | title('Position, Velocity, & Acceleration as a Function of Time') | ||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | subplot(3,1,2) | ||
| + | hold on; | ||
| + | plot(t',v1,'b') | ||
| + | plot(t',v2,'c') | ||
| + | ylabel('Velocity (m/s)') | ||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | subplot(3,1,3) | ||
| + | hold on; | ||
| + | plot(t',a1,'g') | ||
| + | ylabel('Acceleration (m/s^2)') | ||
| + | xlabel('time (1 = 0.01 detik)') | ||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | |||
| + | toc | ||
| + | |||
| + | |||
| + | ===Hasil=== | ||
| + | |||
| + | [[File:Artikelkomtekevi25.JPG]] | ||
| + | |||
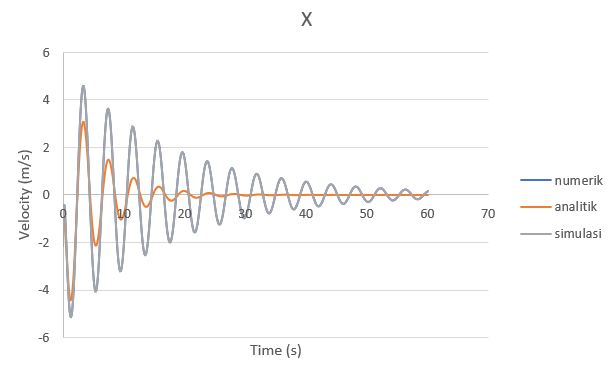
| + | Gambar 2. Grafik velocity (dx/dt) perbandingan analitik, numerik, dan simulasi | ||
| + | |||
| + | [[File:Artikelkomtekevi26.JPG]] | ||
| + | |||
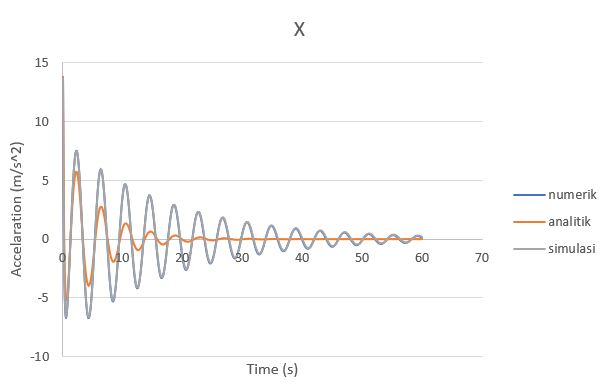
| + | Gambar 3. Grafik acceleration (d^2x/dt^2) perbandingan analitik, numerik, dan simulasi | ||
| + | |||
| + | [[File:Artikelkomtekevi27.JPG]] | ||
| + | |||
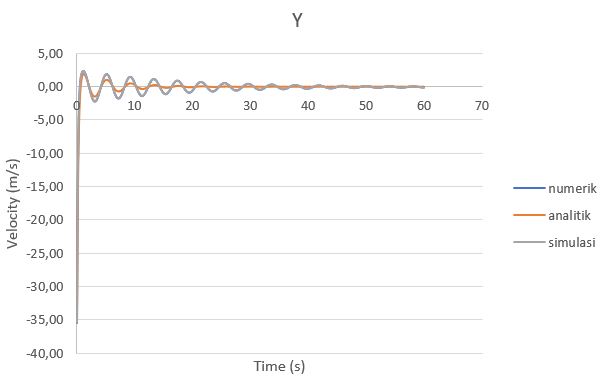
| + | Gambar 4. Grafik velocity (dy/dt) perbandingan analitik, numerik, dan simulasi | ||
| + | |||
| + | Selanjutnya, untuk memverifikasi hasil numerik menggunakan metode euler yang dijelaskan diatas, digunakan metode Artificial Neural Networks (ANN) pada perangkat lunak matlab. Berikut sedikit pengenalan tentang ANN yang dapat kita temui dari beberapa sumber di internet. ANN adalah beberapa lapisan jaringan saraf (neural network) yang terhubung secara keseluruhan yang dapat dilihat dari gambar dibawah ini. Setiap node pada setiap lapisan terhubung ke setiap node dari lapisan selanjutnya. Jaringan dibuat lebih dalam dengan menambah jumlah lapisan tersembunyi (hidden layer). | ||
| + | |||
| + | [[File:Artikelkomtekevi28.JPG]] | ||
| + | |||
| + | Jika salah satu hidden layer atau node output diperbesar, maka akan ditemukan gambar dibawah ini. | ||
| + | |||
| + | [[File:Artikelkomtekevi29.JPG]] | ||
| + | |||
| + | Node tertentu mengambil jumlah bobot dari inputnya, dan meneruskannya melalui fungsi aktivasi non-linear. Ini merupakan output dari node yang kemudian menjadi input dari node yang lain pada layer selanjutnya. Sinyal mengalir dari kiri ke kanan, dan output akhir dihitung dengan cara melakukan prosedur ini untuk semua node. Melatih jaringan saraf berarti mempelajari bobot yang terkait dengan semua edge. | ||
| + | |||
| + | Metode ANN ini digunakan untuk melatih data-data yang didapat dari numerik, dimana nilai posisi pada sumbu x dan y digunakan sebagai nilai input, dan nilai kecepatan pada sumbu x (u) dan sumbu y (v) yang merupakan hasil diferensial dari posisi digunakan sebagai nilai target. Data yang di training sebanyak 400 data. | ||
| + | |||
| + | [[File:Artikelkomtekevi30.JPG]] | ||
| + | |||
| + | Dengan demikian, diperoleh hasil yang dapat dilihat pada gambar diatas, dengan nilai R sebesar 0,99996 yang berarti data yang didapat dari metode Euler terverifikasi secara baik dengan persamaan yang dihasilkan dari metode ANN pada matlab. | ||
| + | |||
| + | ===Kesimpulan=== | ||
| + | |||
| + | Dari hasil yang sudah didapat untuk metode analitik, numerik, dan simulasi berikut beberapa hal yang dapat disimpulkan: | ||
| + | a) Hasil perhitungan numerik terhadap simulasi memiliki nilai yang berimpit. Hal ini dikarenakan, pada dasarnya simulasi yang dilakukan dengan MATLAB, menggunakan cara yang sama dengan numerik, hanya saja pada numerik persamaan-persamaannya harus dirubah menjadi 3 persamaan dengan orde 1. Sedangan pada simulasi, persamaan dari FBD langsung menjadi input pada MATLAB. | ||
| + | b) Hasil perhitungan numerik dan simulasi berbeda dengan metode analitik. Seperti sudah disebutkan pada materi perkuliahan sebelum ini, bahwa pada metode Forward Euler terdapat hal yang harus diperhatikan pada perkembangan amplitudonya. | ||
| + | c) Hasil metode forward euler telah terverifikasi dengan metode Artificial Neural Networks (ANN) yang dapat dilihat dari nilai R sebesar 0,99996 (mendekati 1) dari persamaan output metode ANN menggunakan software matlab. | ||
| + | |||
| + | ==Artikel 2, Simplified Finite Elements model to represent Mass-Spring structures in dynamic simulation== | ||
| + | |||
| + | |||
| + | Kasus ini menjelaskan sebuah sistem 2 cart spring-mass-damper. Persamaan gerak untuk system 2 degree of freedom yang digunakan adalah Newtonian mechanics dan diselesaikan secara numerik pada matlab. | ||
| + | |||
| + | [[File:FBD-MS-FES.jpg]] | ||
| + | % Calculates the position, velocity, and acceleration as a function of time | ||
| + | % of a system of carts connected by springs and dashpots. Euler's Method is | ||
| + | % used to solve the equations of motion numerically. | ||
| + | clear all; close all; clc; | ||
| + | tic | ||
| + | |||
| + | % Problem parameters | ||
| + | k1=50; % cart 1 spring constant (N/m) | ||
| + | k2=50; % cart 2 spring constant (N/m) | ||
| + | b1=3; % cart 1 viscous damping coefficient (kg/s) | ||
| + | b2=3; % cart 2 viscous damping coefficient (kg/s) | ||
| + | m1=5; % cart 1 mass (kg) | ||
| + | m2=5; % cart 2 mass (kg) | ||
| + | x10=1; % cart 1 initial position (m) | ||
| + | x20=-1; % cart 2 initial position (m) | ||
| + | v10=0; % cart 1 initial velocity (m/s) | ||
| + | v20=0; % cart 2 initial velocity (m/s) | ||
| + | |||
| + | % Set time step stuff | ||
| + | simTime=10; % simulation time (s) | ||
| + | tStep=0.001; % simulation time step | ||
| + | iterations=simTime/tStep; | ||
| + | t=0:iterations; | ||
| + | |||
| + | % Pre-allocate variables for speed and add initial conditions | ||
| + | x1=zeros(iterations,1); | ||
| + | x1(1,:)=x10; | ||
| + | x2=zeros(iterations,1); | ||
| + | x2(1,:)=x20; | ||
| + | v1=zeros(iterations,1); | ||
| + | v1(1,:)=v10; | ||
| + | v2=zeros(iterations,1); | ||
| + | v2(1,:)=v20; | ||
| + | a1=zeros(iterations,1); | ||
| + | a1(1,:)=-(b1*v10-b2*(v20-v10)+k1*x10-k2*(x20-x10))/m1; | ||
| + | a2=zeros(iterations,1); | ||
| + | a2(1,:)=-(b2*(v20-v10)+k2*(x20-x10))/m2; | ||
| + | |||
| + | % Solve the ODE's with Euler's Method | ||
| + | for n=2:(iterations+1) | ||
| + | x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position | ||
| + | x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position | ||
| + | v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity | ||
| + | v2(n,:)=v2(n-1,:)+a2(n-1,:)*tStep; % cart 2 velocity | ||
| + | % Find cart accelerations | ||
| + | a1(n,:)=-(b1*v1(n,:)-b2*(v2(n,:)-v1(n,:))+k1*x1(n,:)-k2*(x2(n,:)-x1(n,:)))/m1; | ||
| + | a2(n,:)=-(b2*(v2(n,:)-v1(n,:))+k2*(x2(n,:)-x1(n,:)))/m2; | ||
| + | end | ||
| + | |||
| + | |||
| + | % Plot results | ||
| + | subplot(3,1,1) | ||
| + | hold on; | ||
| + | plot(t',x1,'r') | ||
| + | plot(t',x2,'m') | ||
| + | ylabel('Position (m)') | ||
| + | title('Position, Velocity, & Acceleration as a Function of Time') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | subplot(3,1,2) | ||
| + | hold on; | ||
| + | plot(t',v1,'b') | ||
| + | plot(t',v2,'c') | ||
| + | ylabel('Velocity (m/s)') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | subplot(3,1,3) | ||
| + | hold on; | ||
| + | plot(t',a1,'g') | ||
| + | plot(t',a2,'y') | ||
| + | ylabel('Acceleration (m/s^2)') | ||
| + | xlabel('time (iterations)') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | |||
| + | toc | ||
| + | |||
| + | [[File:Artikelkeduaevi.jpg]] | ||
| + | |||
| + | Akan tetapi pada kasus ini, pembahasan yang dilakukan masih dengan Mass-Spring method. Untuk Finite Element Simplified (FES), akan diupdate pada kesempatan selanjutnya. | ||
| + | |||
| + | Source: https:// www.youtube.com/ watch?v=N524t6wdlcM&feature=youtu.be | ||
| + | |||
| + | == Artikel 3 ANALISIS MASS SPRING PADA BANGUNAN == | ||
| + | |||
| + | '''PENDAHULUAN''' | ||
| + | |||
| + | Sistem pemodelan yang digunakan dalam struktur bangunan ini adalah pemodelan tiga derajat kebebasan (3 DOF). Gambar 1 menunjukkan model struktur bangunan bertingkat yang ditandai dengan adanya perpindahan sebesar x2 dan x3 karena pengaruh beban input gaya eksitasi dari shaking table. Sedangkan untuk pemodelan matematis, diperoleh persamaan dari free body diagram sistem yang akan dianalisa. | ||
| + | |||
| + | [[File:Bangunanevi1.JPG]] | ||
| + | |||
| + | Untuk free body diagram dan persamaan massa shaking table (M1) adalah : | ||
| + | |||
| + | [[File:Bangunanevi2.JPG]] | ||
| + | |||
| + | [[File:Bangunanevi3.JPG]] | ||
| + | |||
| + | Setelah mendapatkan nilai parameter yang dibutuhkan untuk simulasi, Input yang digunakan yaitu input sinusoidal dengan frekuensi operasi 7 Hz atau 43,982 rad/s. | ||
| + | |||
| + | Untuk menyelesaikan persamaan gerak di atas maka dilakukan penyederhanaan persamaan menjadi 1 persamaan orde 6, dengan mengasumsikan x1 sebagai x, x2 sebagai y, dan x3 sebagai z, sehingga diperoleh persamaan, | ||
| + | |||
| + | [[File:Bangunanevi4.JPG]] | ||
| + | |||
| + | Persamaan 4 disubtitusikan kepersamaan 2 sehingga didapatkan persamaan, | ||
| + | |||
| + | [[File:Bangunanevi5.JPG]] | ||
| + | |||
| + | Untuk mencari nilai akar-akar dari persamaan di atas maka digunakan matlab untuk mempermudah perhitungan, | ||
| + | |||
| + | p=[1.154 21.059 4153.743 42436.977 2396974.157 2858796.484 151595214.4]; | ||
| + | r=roots(p) | ||
| + | r = | ||
| + | -3.6221 +52.7481i | ||
| + | -3.6221 -52.7481i | ||
| + | -5.5262 +24.9446i | ||
| + | -5.5262 -24.9446i | ||
| + | 0.0239 + 8.4846i | ||
| + | 0.0239 - 8.4846i | ||
| + | |||
| + | [[File:Bangunanevi6.JPG]] | ||
| + | |||
| + | Lalu dengan mengasumsikan nilai konstanta, | ||
| + | A=-0.0005 | ||
| + | B=0.0001 | ||
| + | C=0.0001 | ||
| + | D=-0.0002 | ||
| + | E=0.00032 | ||
| + | F=-0.009 | ||
| + | G=0.00008 | ||
| + | H=0.00001 | ||
| + | |||
| + | Maka dengan menggunakan software MATLAB dapat dibuat grafik posisi terhadap waktu. Berikut coding yang menjadi input dalam MATLAB: | ||
| + | |||
| + | syms x t A B C D E F | ||
| + | A=-0.0005 | ||
| + | B=0.0001 | ||
| + | C=0.0001 | ||
| + | D=-0.0002 | ||
| + | E=0.00032 | ||
| + | F=-0.009 | ||
| + | G=0.00008 | ||
| + | H=0.00001 | ||
| + | |||
| + | t=(1:100)/10 | ||
| + | x1 = exp(-3.62*t)*(A*sin(52.75*t) + B*cos(52.75*t)) + exp(5.53*t)* | ||
| + | (C*sin(24.94*t) + D*cos(24.94*t)) + exp(0.024*t)*(E*sin(8.48*t) + | ||
| + | F*cos(8.48*t)) + G*sin(43.982*t) + H*cos(43.982*t) | ||
| + | % Plot results | ||
| + | subplot(1,1,1) | ||
| + | hold on; | ||
| + | plot(t',x1,'r') | ||
| + | ylabel('Position (m)') | ||
| + | |||
| + | [[File:Bangunanevi7.JPG]] | ||
| + | |||
| + | Gambar 5 Grafik respon posisi terhadap waktu | ||
| + | |||
| + | Grafik di atas menunjukan pengaruh getaran pada bagian bawah struktur pemodelan bangunan di mana perubahan arah gerak pada bagian bawah struktur membentuk pola sinusoidal yang menandakan adanya gerak bolak-balik pada struktur tersebut. | ||
| + | |||
| + | '''KESIMPULAN''' | ||
| + | |||
| + | Dalam permasalahan analisis gerak (perubahan arah, kecepatan dan percepatan) dapat dilakukan dengan metode lain berupa FES, namun pada artikel ini pemodelan FES belum dilakukan. Artikel ini hanya membahan mass-spring (MS) model yang terjadi pada suatu sistem pemodelan bangunan yang diberikan getaran. Sehingga dapat dilihat perilaku gerak bangunan sebagai respon dari adanya getaran yang diberikan. | ||
| + | |||
| + | '''REFERENSI''' | ||
| + | |||
| + | • Syaldiles Putri Indahdinata, Analisis Pengaruh Perubahan Cross Sectional Area Dan Posisi Peletakan Tuned Liquid Column Damper Terhadap Respon Dinamis Model Struktur Bangunan Bertingkat, Departemen Teknik Mesin FTI-ITS Surabaya, 2018. | ||
| + | |||
| + | ==UAS== | ||
| + | |||
| + | [[File:Uasevi1.jpg|600px]] | ||
| + | |||
| + | [[File:Uasevi2.JPG]] | ||
| + | |||
| + | [[File:Uasevi3.png]] | ||
Latest revision as of 23:48, 29 September 2021
Contents
- 1 Pendahuluan Komputasi Teknik
- 2 Quiz
- 3 Model Komputasi Teknik
- 4 Optimasi Kebutuhan Energi Manusia
- 5 9 Maret 2020
- 6 UTS
- 7 Quiz Oscillating dynamic system
- 8 Artikel 1, OSCILLATING 1-D DYNAMIC SYSTEM
- 9 Artikel 2, Simplified Finite Elements model to represent Mass-Spring structures in dynamic simulation
- 10 Artikel 3 ANALISIS MASS SPRING PADA BANGUNAN
- 11 UAS
Pendahuluan Komputasi Teknik
I. Pengertian
Komputasi teknik adalah suatu kegiatan menambah, kurang, kali, bagi angka-angka yang disebut numerik dari eksak dengan menggunakan komputer. Inti berfikir dalam pemograman adalah input-proses-output. Dimana algoritma manusia dalam dipindahkan dalam bentuk algoritma computer, yang disebut dengan bahasa pemograman.
II. Tujuan Pembelajaran
1. Mampu memahami konsep-konsep dan prinsip-prinsip didalam pelajaran komputasi teknik, seperti konsep iterasi, konsep error (floating point error), dsb.
2. Mampu menerapkan pemahaman tersebut dalam menyelesaikan masalah didalam masyarakat
3. Memiliki pengenalan diri yang lebih tentang muhasabah, skill, value, dsb.
Quiz
Model Komputasi Teknik
Pengerjaan skripsi saya menggunakan perangkat lunak inventor yang didasarkan pada Finite Element Method (FEM) untuk stress analysis. FEM adalah model perhitungan numerik yang menemukan perkiraan solusi untuk masalah persamaan differensial parsial dan integrasi lainnya yang dihasilkan dari hasil diskritisasi benda kontinum. Apa yang dilakukan FEM adalah membagi sebuah masalah besar menjadi bagian-bagian yang lebih kecil dan sederhana. Dalam Autodesk Inventor Stress Analysis, itu membutuhkan struktur yang complex dan mengubahnya menjadi bagian-bagian lebih kecil (meshing process) dan kemudian menyelesaikan persamaan dengan sistem persamaan yang memiliki input yang berbeda-beda, seperti constraints, materials, and loads.
In stress analysis, the weak form is called the principle of virtual work.
dimana,
w = deflection
u = displacement
A = area
E = young’s modulus
b = axial loading
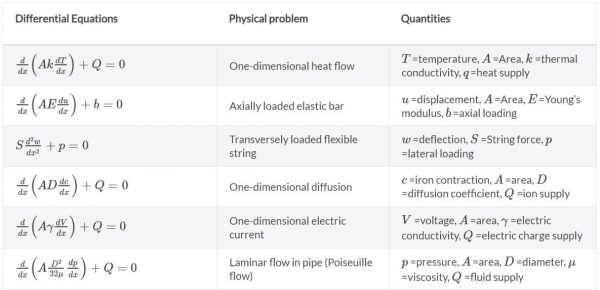
Untuk persamaan lainnya terkait Finite Element Analysis dapat dilihat pada tabel dibawah ini,
source: https: //www. simscale.com/docs/content/simwiki/fea/whatisfea.html
Optimasi Kebutuhan Energi Manusia
Sebagai unit dari energi, kalori mengacu pada energi yang diperoleh dari makanan dan minuman yang kita konsumsi setiap hari. Kalori sangat penting bagi tubuh manusia. Tanpa kalori, sel-sel dalam tubuh akan mati, dan organ-organ vital seperti jantung dan paru-paru tidak akan mampu melaksanakan fungsi dasarnya.
Di Indonesia, berdasarkan rekomendasi Angka Kecukupan Gizi (AKG) dari Kementerian Kesehatan RI, rata-rata kebutuhan untuk pria usia 30 – 49 tahun adalah 2625 kkal per hari. Sedangkan perempuan usia 30 – 49 tahun adalah 2150 kkal per hari, demikian seperti dikutip dari laman depkes.go,id.
Menghitung Kalori
Terdapat dua jenis kalori, yaitu kalori kecil yang ditulis dalam satuan “kal” dan kalori besar atau “kilokalori” (kkal), dengan perhitungan 1 kkal sama dengan 1.000 kal. Cara menghitung kalori yang kita butuhkan menurut P2PTM Kemenkes RI sangat sederhana, karena hanya berdasarkan jenis kelamin dan tinggi badan. Sebelum menghitung, kita harus mengetahui terlebih dahulu tinggi badan (TB) dalam sentimenter dan Berat Badan Ideal (BBI) dengan rumus sebagai berikut:
BBI = (TB-100) – (10% x (TB – 100))
Selanjutnya, kita dapat hitung Kebutuhan Kalori Basal (KKB) atau Basal Metabolic Rate (BMR). KKB merupakan kebutuhan kalori yang dibutuhkan oleh tubuh untuk metabolisme basal, yakni metabolisme yang wajib dilakukan mahluk hidup walaupun tidak membutuhkan energi. Ini berarti metabolisme tubuh akan tetap berjalan meskipun dalam keadaan tidur atau tidak melakukan apa-apa. Berikut adalah rumus menghitung angka KKB:
KKB Laki-laki = 30 kkal x BBI
KKB Perempuan = 25 kkal x BBI
Menghitung Kebutuhan Kalori Total (KKT)
Kebutuhan kalori total adalah jumlah kebutuhan kalori tubuh ditambah dengan jumlah kalori saat melakukan aktivitas fisik. Kita mengenal tiga jenis aktivitas, yaitu
1. Aktivitas ringan seperti membaca (10%), menyetir mobil (10%), kerja kantoran (10%), mengajar (20%), berjalan (20%).
2. Aktivitas sedang: kerja rumah tangga (20%), jalan cepat (30%), bersepeda (30%).
3. Aktivitas berat: aerobik (40%), mendaki (40%), dan jogging (40%)
Rumus KKT = KKB + Aktivitas Fisik - Faktor Koreksi
Faktor koreksi adalah sebagai berikut:
Usia 40 - 59 tahun, nilai koreksinya minus 5%
Usia 60 - 69 tahun, nilai koreksinya minus 10%
Usia >70 tahun, nilai koreksinya minus 20%
Resource: https:// www.anlene.com/id/ms/berapa-banyak-kalori-yang-anda-butuhkan-setiap-hari.html
9 Maret 2020
Berikut tahapan dalam menganalisa suatu masalah:
1. Initial thinking (analisis) untuk mengidentifikasi masalah (objektif) yang akan diselesaikan, dapat berupa masalah terstruktur yakni terkait SOP, dan unstructured issue terkait modifikasi.
2. Mengembangkan rumusan (permodelan matematis) yang mengandung asumsi (tergantung pengetahuan, ilmu, dan pengalaman kita), dimana asumsi sama dengan batasan masalah.
3. Pengumpulan data yang dibutuhkan untuk menyelesaikan permodelan matematis diatas.
4. Simulasi = menjalankan atau mengeksekusi model (constraint) yang kita buat dengan suatu variabel bebas
5. Verifikasi = resolve the equation right, menguji apakah model yang dilakukan tidak ada kesalahan numerik, contohnya kesalahan ngitung, pada proses meshing
6. Validasi = resolve the right equation, menguji kebenaran / keaktualan dari hasil simulasi tadi
7. Result dan discussion
8. Recommendation
UTS
Video presentasi
Video presentasi hasil belajar terkait pengetahuan (konsep/teori) dan keterampilan (menggunakan komputasi teknik)
Laporan tugas optimasi
Laporan hasil tugas optimasi kebutuhan energi manusia.
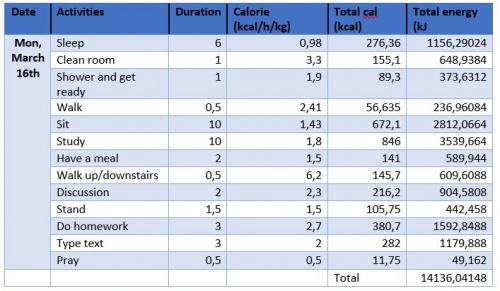
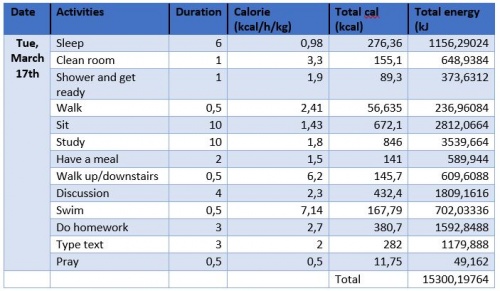
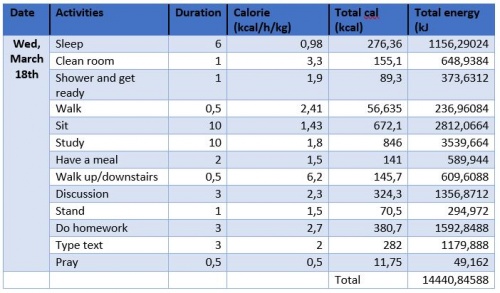
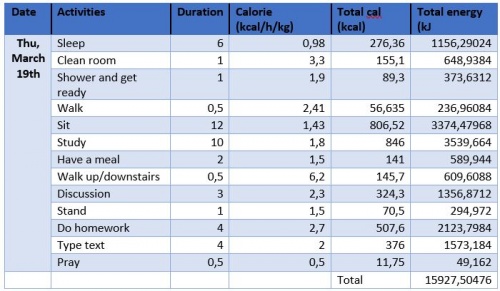
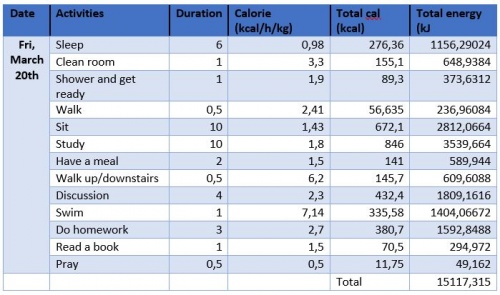
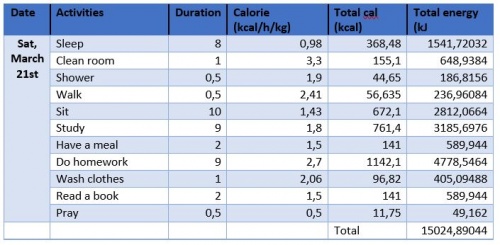
Berdasarkan hasil diskusi kelas pada ( http://air.eng.ui.ac.id/index.php?title=Optimasi_Sistem_Energi_pada_Manusia ) ini, berikut optimasi kebutuhan energi saya pribadi selama seminggu (March 16th - 22nd),
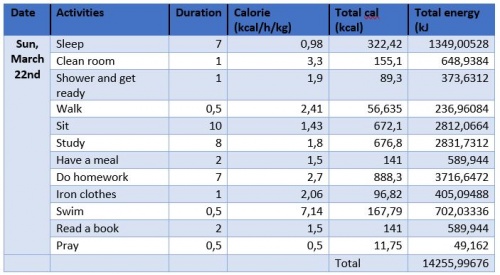
Kebutuhan kalori yang saya butuhkan dalam 1 minggu:
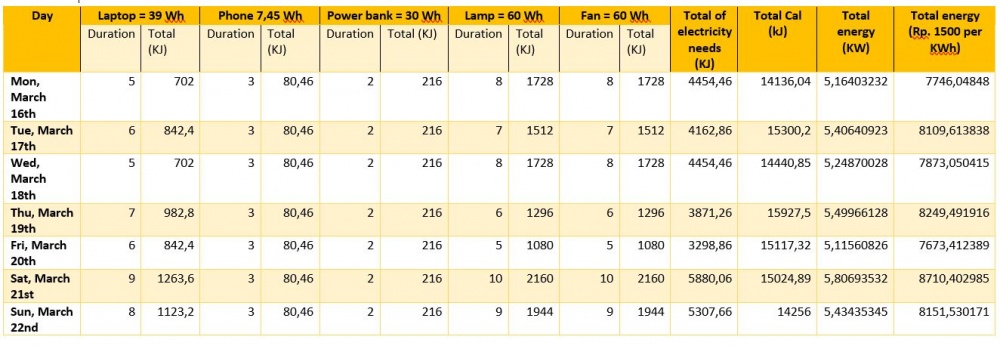
Kebutuhan listrik yang saya butuhkan dalam 1 minggu:
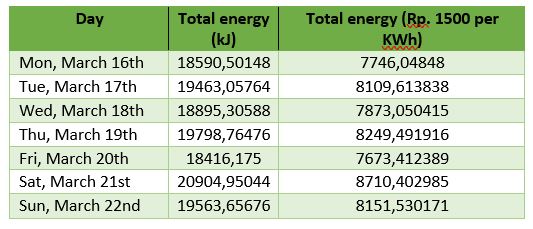
Sehingga diperoleh total energi dan total biaya yang saya butuhkan dalam seminggu:
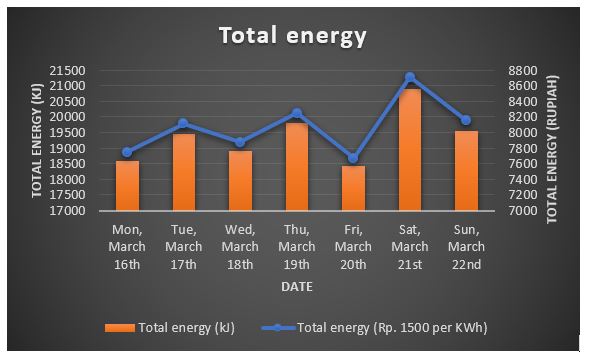
Dan menghasilkan grafik sebagai berikut:
Quiz Oscillating dynamic system
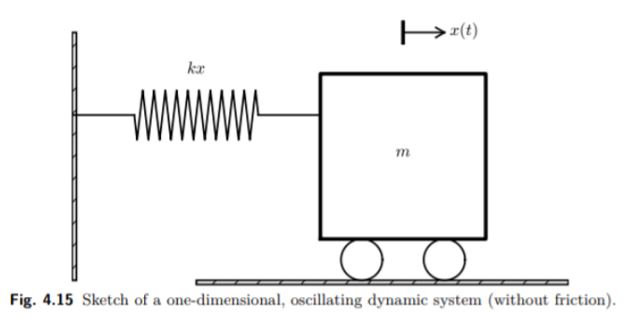
Memverifikasi sebuah sistem dinamik berosilasi tanpa gesekan (fig. 4.15) dengan menggunakan metode numerik dan metode analitik. Selain itu, terdapat 2 metode numerik yang akan digunakan, yakni standard numerical solution (persamaan 4.47 dan 4.48) dan a magic fix of a numerical method (persamaan 4.49 dan 4.50).
Gambar diatas menjelaskan suatu benda dengan massa m melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan. Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) body (penampang m) kembali dan bekerja "melawan" gerakan, misalkan x (t) adalah posisi body pada sumbu x, dimana body bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (mis., Tidak ada gesekan). Hukum kedua Newton menyatakan F=ma kemudian memiliki F=-kx dan a=x",
-kx = mx" (4.41)
sehingga dapat dituliskan
x" + ω^2 x = 0 (4.42)
Persamaan (4.42) adalah persamaan diferensial orde kedua, dan oleh karena itu kita memerlukan dua kondisi awal, satu pada posisi x(0) dan satu pada kecepatan x’(0).
x (0) = 1,5 dan x’(0) = 0
Untuk mengendalikan turunan orde dua menggunakan metode numerik, cara yang dapat kita tuliskan pada persamaan 4.42 sebagai sebuah sistem orde pertama dari 2 persamaan turunan. Kita memperkenalkan u=x dan v=x'=u' sebagai 2 fungsi baru yang tidak diketahui. Dua persamaan yang sesuai muncul dari definisi v=u' dan persamaan asal (4.42):
u' = v (4.43)
v' = -ω²u (4.44)
maka u"=v' untuk menghilangkan turunan orde kedua dari hukum kedua newton.
Dengan menggunakan metode numerik pertama, yakni standard numerical solution dengan persamaan-persamaan berikut:
u^(n+1) = u^n + ∆t v^n (4.47)
v^(n+1) = v^n - ∆t ω^2 u^n (4.48)
Selain itu, terdapat juga metode numerik kedua yang anggap lebih akurat, disebut a magic fix of the numerical method dengan mengganti u^n untuk persamaan kedua menjadi u^(n+1) dari persamaan pertama, sehingga:
u^(n+1) = u^n + ∆t v^n (4.49)
v^(n+1) = v^n - ∆t ω^2 u^(n+1) (4.50)
dimana diketahui ω = 2,5 rad/s dan ∆t = 0,05 s, maka dilakukan perhitungan sebagai berikut.
Selanjutnya dilakukan verifikasi antara setiap metode numerik diatas terhadap metode analitik, dimana persamaan-persamaan untuk metode analitik adalah sebagai berikut:
u = x cos ωt
v = -x ω cos ωt
yang perhitungan detail nya dapat juga dilihat pada lampiran (ms.excel).
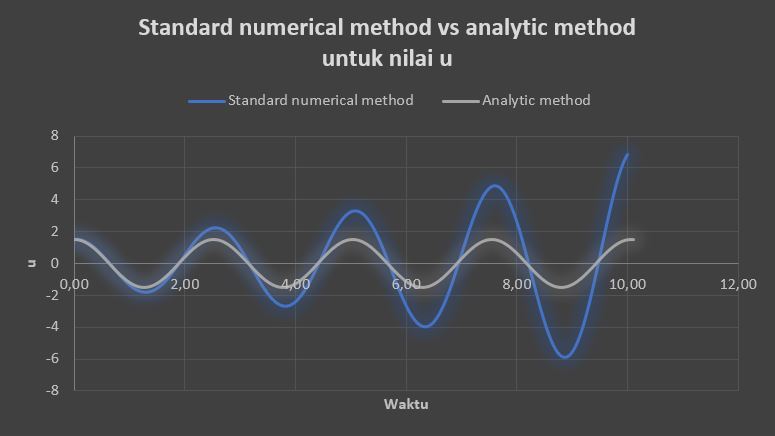
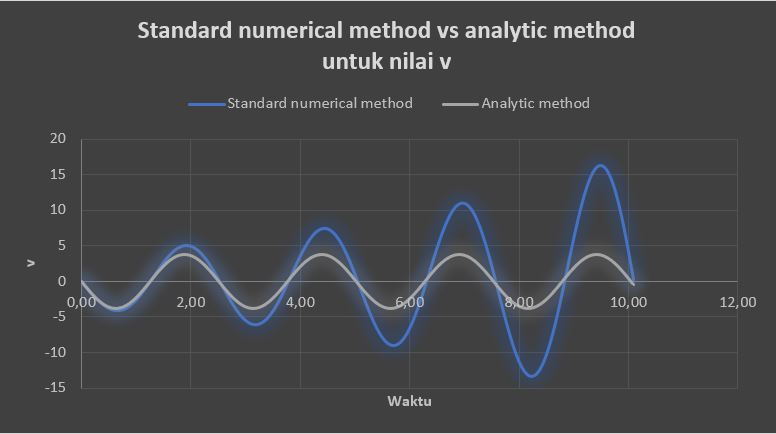
Sehingga diperoleh hasil yang merupakan grafik sebagai berikut:
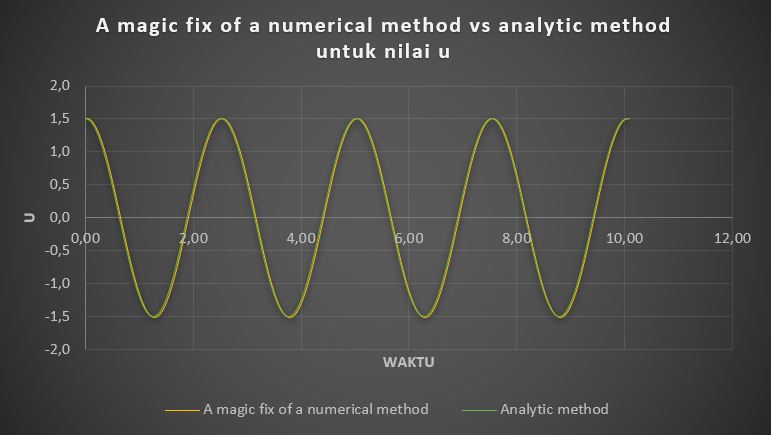
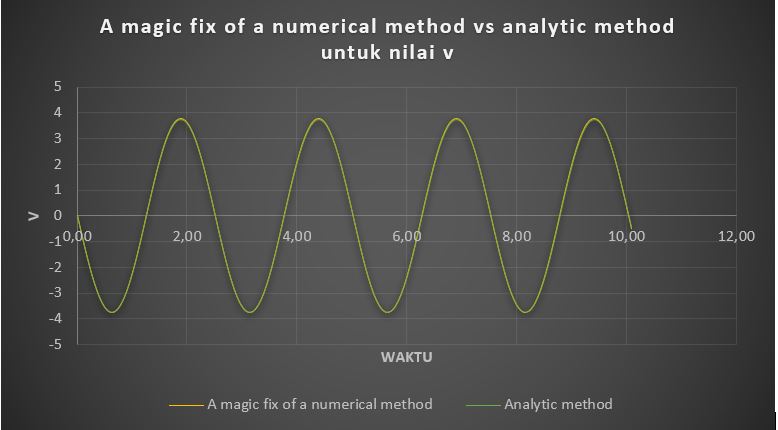
Dari kedua grafik diatas dapat dilihat jelas bahwa metode numerik yang standard dengan menggunakan persamaan 4.47 dan 4.48 jauh dari kata akurat, dikarenakan hasil yang didapat dari metode ini (grafik biru) sangat berbeda dengan hasil dari metode analitik (grafik abu-abu). Oleh karena itu, metode numerik yang disebut a magic fix for a numerical method perlu dilakukan, dengan hasil sebagai berikut:
Dari kedua grafik diatas, dapat dilihat bahwa metode numerik ini (grafik kuning) memiliki tingkat keakurasian yang sangat baik dengan pemverifikasian terhadap metode analitik (grafik hijau). Dengan demikian, disimpulkan bahwa a magic fix for a numerical method telah terverifikasi terhadap metode analitik yang mana dapat mewakili metode analitik. untuk menentukan nilai u dan v.
Artikel 1, OSCILLATING 1-D DYNAMIC SYSTEM
Pendahuluan
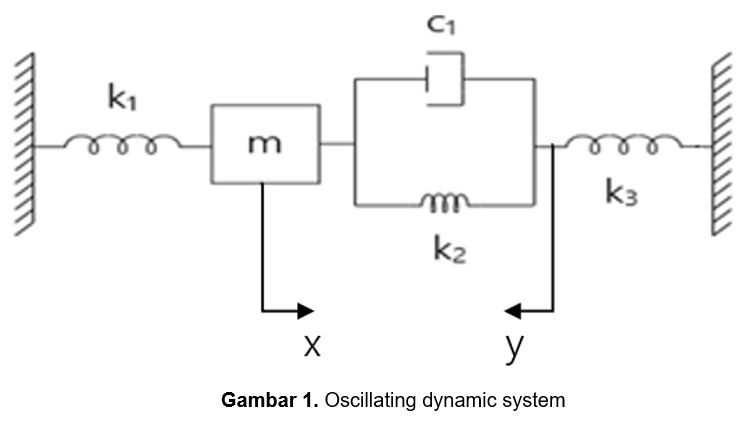
Artikel ini akan membahas penyelesaian permasalahan oscillating 1-D dynamic system pada system damping sesuai gambar di bawah. Pada system di bawah terdapat sebuah massa yang dihubungkan dengan 3 spring, dan 1 dashpot. System tersebut fix pada 2 boundary sisi kiri dan kanan.
Penyelesaian dari permasalahan tersebut akan dilakukan dengan 3 metode, yang kemudian akan dibandingkan hasil dari perhitungan pada tiap metode tersebut. Metode yang digunakan yaitu: analitikal, numerik, dan simulasi. Pada metode analitikal dilakukan tinjauan gaya aksi – reaksi pada free body diagram (FBD) yang muncul dari eksitasi yang diberikan. Kemudian untuk penyelesaian metode numerik akan dilakukan iterasi dengan bantuan software Microsoft Excel menggunakan Forward Euler. Sedangkan untuk proses simulasi akan dilakukan dengan bantuan software MATLAB.
Metode
Metode Analitik
Free Body Diagram (FBD):
• Tinjauan massa:
• Tinjauan titik: (diantara c1, k2, dan k3)
Diketahui:
Maka persamaan 1 dan 2 dapat dituliskan kembali menjadi;
Persamaan 1
Persamaan 2
Penyelesaian
Asumsi
Karena pada persamaan 5 masih terdapat ̇ y maka subtitusi persamaan 6 ke persamaan 5, sehingga didapatkan nilai ̇ z sebagai berikut;
Penyelesaian menggunakan matrix;
Maka didapatkan nilai λ sebesar
Sehingga didapatkan persamaan
Jika diasumsikan nilai C1,C2,dan C3 adalah 1, 2 dan 3 maka;
Nilai x untuk t = 0 s, t = 1 s, dan t = 10 s adalah
Mencari nilai yh dengan mensubtitusi nilai xh ke dalam persamaan ̇ z=-x+3y, di mana nilai ̇ z = ̈ x.
Mencari nilai ̇x;
Nilai ̇ x untuk t = 0 s, t = 1 s, dan t = 10 s adalah
Mencari nilai ̈ x;
Persamaan ̈ x di atas dapat disederhanakan menjadi;
Nilai ̈ x untuk t = 0 s, t = 1 s, dan t = 10 s adalah
Mencari nilai y;
Persamaan yh dapat disederhanakan menjadi;
Nilai y untuk t = 0 s, t = 1 s, dan t = 10 s adalah
Mencari nilai ̇ y;
Nilai ̇ y ketika t = 0 s, t = 1 s, dan t = 10 s adalah
Metode Numerik
Metode ini dilakukan dengan menggunakan software Microsoft Excel. Parameter input yang harus diketahui yaitu x pada t = 0 s, y pada t = 0 s, dan selisih penambahan waktu (∆t). Parameter input x dan y ini dapat juga disebut dengan initial condition. Lalu kemudian dilakukan iterasi sesuai dengan ∆t sampai waktu yang ditentukan. Nilai parameter input tersebut didapat dengan cara analitis seperti sudah disebut di atas, yaitu x((t=0))=4 m; y((t=0))=5.9 m; dan selisih waktu ∆t=0.1 second.
Seperti sudah disebutkan sebelumnya bahwa penyelesaiannya menggunakan Forward Euler, yaitu sebagai berikut:
Simulasi
Simulasi dilakukan dengan bantuan software MATLAB. Adapun agar simulasi dapat berjalan, maka perlu diberikan input coding pada software MATLAB yang isinya sebagai berikut.
% Calculates the position, velocity, and acceleration as a function of time % of a system of carts connected by springs and dashpots. Euler's Method is % used to solve the equations of motion numerically. clear all; close all; clc; tic
% Problem parameters k1=1; % cart 1 spring constant (N/m) k2=2; % cart 1 spring constant (N/m) b1=1; % cart 1 viscous damping coefficient (kg/s) m1=1; % cart 1 mass (kg) k3=3; % cart 1 spring constant (N/m) x10=4; % cart 1 initial position (m) x20=5.9; % y movement initial position (m) v10=-2.135; % cart 1 initial velocity (m/s) v20=-35.36; % cart 2 initial velocity (m/s)
% Set time step stuff simTime=60; % simulation time (s) tStep=0.1; % simulation time step iterations=simTime/tStep; t=0:iterations;
% Pre-allocate variables for speed and add initial conditions x1=zeros(iterations,1); x1(1,:)=x10; x2=zeros(iterations,1); x2(1,:)=x20; v1=zeros(iterations,1); v1(1,:)=v10; v2=zeros(iterations,1); v2(1,:)=v20; a1=zeros(iterations,1); a1(1,:)=((0-(k1*x10)-b1*(v10+v20)-k2*(x20+x10))/m1);
% Solve the ODE's with Euler's Method for n=2:(iterations+1) x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity v2(n,:)=-(2*x1(n,:)+5*x2(n,:)+v1(n,:)) % Find cart accelerations a1(n,:)=((0-k1*x1(n,:))-b1*(v1(n,:)+v2(n,:))-k2*(x2(n,:)+x1(n,:))/m1); end
% Plot results
subplot(3,1,1)
hold on;
plot(t',x1,'r')
plot(t',x2,'m')
ylabel('Position (m)')
title('Position, Velocity, & Acceleration as a Function of Time')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
subplot(3,1,2)
hold on;
plot(t',v1,'b')
plot(t',v2,'c')
ylabel('Velocity (m/s)')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
subplot(3,1,3)
hold on;
plot(t',a1,'g')
ylabel('Acceleration (m/s^2)')
xlabel('time (1 = 0.01 detik)')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
toc
Hasil
Gambar 2. Grafik velocity (dx/dt) perbandingan analitik, numerik, dan simulasi
Gambar 3. Grafik acceleration (d^2x/dt^2) perbandingan analitik, numerik, dan simulasi
Gambar 4. Grafik velocity (dy/dt) perbandingan analitik, numerik, dan simulasi
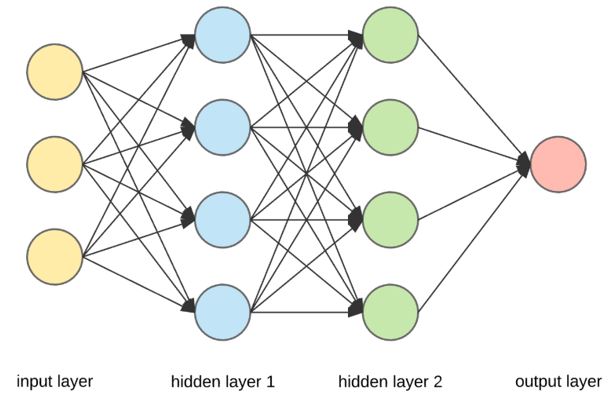
Selanjutnya, untuk memverifikasi hasil numerik menggunakan metode euler yang dijelaskan diatas, digunakan metode Artificial Neural Networks (ANN) pada perangkat lunak matlab. Berikut sedikit pengenalan tentang ANN yang dapat kita temui dari beberapa sumber di internet. ANN adalah beberapa lapisan jaringan saraf (neural network) yang terhubung secara keseluruhan yang dapat dilihat dari gambar dibawah ini. Setiap node pada setiap lapisan terhubung ke setiap node dari lapisan selanjutnya. Jaringan dibuat lebih dalam dengan menambah jumlah lapisan tersembunyi (hidden layer).
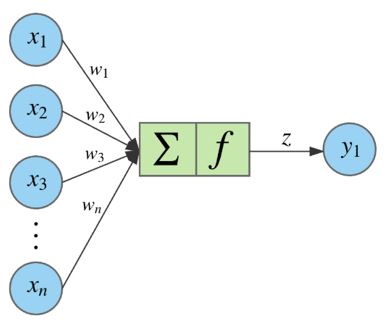
Jika salah satu hidden layer atau node output diperbesar, maka akan ditemukan gambar dibawah ini.
Node tertentu mengambil jumlah bobot dari inputnya, dan meneruskannya melalui fungsi aktivasi non-linear. Ini merupakan output dari node yang kemudian menjadi input dari node yang lain pada layer selanjutnya. Sinyal mengalir dari kiri ke kanan, dan output akhir dihitung dengan cara melakukan prosedur ini untuk semua node. Melatih jaringan saraf berarti mempelajari bobot yang terkait dengan semua edge.
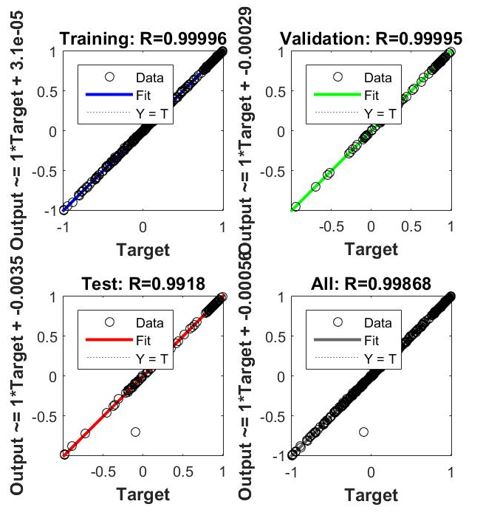
Metode ANN ini digunakan untuk melatih data-data yang didapat dari numerik, dimana nilai posisi pada sumbu x dan y digunakan sebagai nilai input, dan nilai kecepatan pada sumbu x (u) dan sumbu y (v) yang merupakan hasil diferensial dari posisi digunakan sebagai nilai target. Data yang di training sebanyak 400 data.
Dengan demikian, diperoleh hasil yang dapat dilihat pada gambar diatas, dengan nilai R sebesar 0,99996 yang berarti data yang didapat dari metode Euler terverifikasi secara baik dengan persamaan yang dihasilkan dari metode ANN pada matlab.
Kesimpulan
Dari hasil yang sudah didapat untuk metode analitik, numerik, dan simulasi berikut beberapa hal yang dapat disimpulkan: a) Hasil perhitungan numerik terhadap simulasi memiliki nilai yang berimpit. Hal ini dikarenakan, pada dasarnya simulasi yang dilakukan dengan MATLAB, menggunakan cara yang sama dengan numerik, hanya saja pada numerik persamaan-persamaannya harus dirubah menjadi 3 persamaan dengan orde 1. Sedangan pada simulasi, persamaan dari FBD langsung menjadi input pada MATLAB. b) Hasil perhitungan numerik dan simulasi berbeda dengan metode analitik. Seperti sudah disebutkan pada materi perkuliahan sebelum ini, bahwa pada metode Forward Euler terdapat hal yang harus diperhatikan pada perkembangan amplitudonya. c) Hasil metode forward euler telah terverifikasi dengan metode Artificial Neural Networks (ANN) yang dapat dilihat dari nilai R sebesar 0,99996 (mendekati 1) dari persamaan output metode ANN menggunakan software matlab.
Artikel 2, Simplified Finite Elements model to represent Mass-Spring structures in dynamic simulation
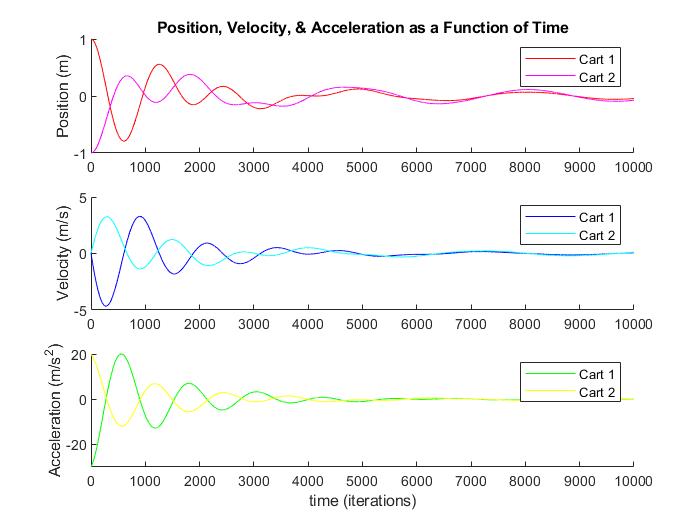
Kasus ini menjelaskan sebuah sistem 2 cart spring-mass-damper. Persamaan gerak untuk system 2 degree of freedom yang digunakan adalah Newtonian mechanics dan diselesaikan secara numerik pada matlab.
% Calculates the position, velocity, and acceleration as a function of time % of a system of carts connected by springs and dashpots. Euler's Method is % used to solve the equations of motion numerically. clear all; close all; clc; tic % Problem parameters k1=50; % cart 1 spring constant (N/m) k2=50; % cart 2 spring constant (N/m) b1=3; % cart 1 viscous damping coefficient (kg/s) b2=3; % cart 2 viscous damping coefficient (kg/s) m1=5; % cart 1 mass (kg) m2=5; % cart 2 mass (kg) x10=1; % cart 1 initial position (m) x20=-1; % cart 2 initial position (m) v10=0; % cart 1 initial velocity (m/s) v20=0; % cart 2 initial velocity (m/s) % Set time step stuff simTime=10; % simulation time (s) tStep=0.001; % simulation time step iterations=simTime/tStep; t=0:iterations; % Pre-allocate variables for speed and add initial conditions x1=zeros(iterations,1); x1(1,:)=x10; x2=zeros(iterations,1); x2(1,:)=x20; v1=zeros(iterations,1); v1(1,:)=v10; v2=zeros(iterations,1); v2(1,:)=v20; a1=zeros(iterations,1); a1(1,:)=-(b1*v10-b2*(v20-v10)+k1*x10-k2*(x20-x10))/m1; a2=zeros(iterations,1); a2(1,:)=-(b2*(v20-v10)+k2*(x20-x10))/m2;
% Solve the ODE's with Euler's Method
for n=2:(iterations+1)
x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position
x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position
v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity
v2(n,:)=v2(n-1,:)+a2(n-1,:)*tStep; % cart 2 velocity
% Find cart accelerations
a1(n,:)=-(b1*v1(n,:)-b2*(v2(n,:)-v1(n,:))+k1*x1(n,:)-k2*(x2(n,:)-x1(n,:)))/m1;
a2(n,:)=-(b2*(v2(n,:)-v1(n,:))+k2*(x2(n,:)-x1(n,:)))/m2;
end
% Plot results
subplot(3,1,1)
hold on;
plot(t',x1,'r')
plot(t',x2,'m')
ylabel('Position (m)')
title('Position, Velocity, & Acceleration as a Function of Time')
legend('Cart 1','Cart 2')
subplot(3,1,2)
hold on;
plot(t',v1,'b')
plot(t',v2,'c')
ylabel('Velocity (m/s)')
legend('Cart 1','Cart 2')
subplot(3,1,3)
hold on;
plot(t',a1,'g')
plot(t',a2,'y')
ylabel('Acceleration (m/s^2)')
xlabel('time (iterations)')
legend('Cart 1','Cart 2')
toc
Akan tetapi pada kasus ini, pembahasan yang dilakukan masih dengan Mass-Spring method. Untuk Finite Element Simplified (FES), akan diupdate pada kesempatan selanjutnya.
Source: https:// www.youtube.com/ watch?v=N524t6wdlcM&feature=youtu.be
Artikel 3 ANALISIS MASS SPRING PADA BANGUNAN
PENDAHULUAN
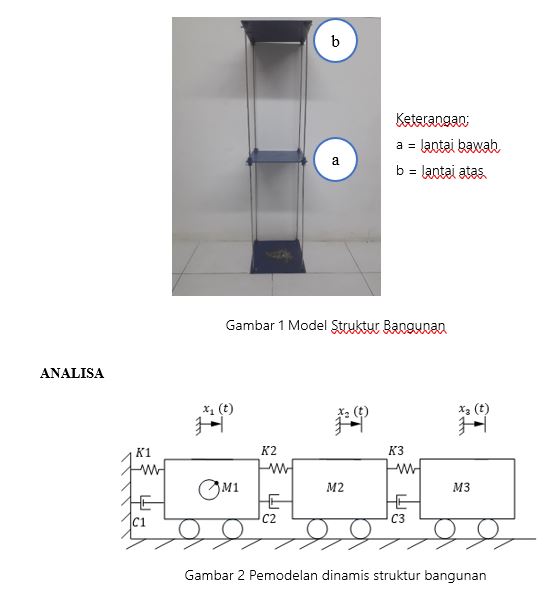
Sistem pemodelan yang digunakan dalam struktur bangunan ini adalah pemodelan tiga derajat kebebasan (3 DOF). Gambar 1 menunjukkan model struktur bangunan bertingkat yang ditandai dengan adanya perpindahan sebesar x2 dan x3 karena pengaruh beban input gaya eksitasi dari shaking table. Sedangkan untuk pemodelan matematis, diperoleh persamaan dari free body diagram sistem yang akan dianalisa.
Untuk free body diagram dan persamaan massa shaking table (M1) adalah :
Setelah mendapatkan nilai parameter yang dibutuhkan untuk simulasi, Input yang digunakan yaitu input sinusoidal dengan frekuensi operasi 7 Hz atau 43,982 rad/s.
Untuk menyelesaikan persamaan gerak di atas maka dilakukan penyederhanaan persamaan menjadi 1 persamaan orde 6, dengan mengasumsikan x1 sebagai x, x2 sebagai y, dan x3 sebagai z, sehingga diperoleh persamaan,
Persamaan 4 disubtitusikan kepersamaan 2 sehingga didapatkan persamaan,
Untuk mencari nilai akar-akar dari persamaan di atas maka digunakan matlab untuk mempermudah perhitungan,
p=[1.154 21.059 4153.743 42436.977 2396974.157 2858796.484 151595214.4]; r=roots(p) r = -3.6221 +52.7481i -3.6221 -52.7481i -5.5262 +24.9446i -5.5262 -24.9446i 0.0239 + 8.4846i 0.0239 - 8.4846i
Lalu dengan mengasumsikan nilai konstanta, A=-0.0005 B=0.0001 C=0.0001 D=-0.0002 E=0.00032 F=-0.009 G=0.00008 H=0.00001
Maka dengan menggunakan software MATLAB dapat dibuat grafik posisi terhadap waktu. Berikut coding yang menjadi input dalam MATLAB:
syms x t A B C D E F A=-0.0005 B=0.0001 C=0.0001 D=-0.0002 E=0.00032 F=-0.009 G=0.00008 H=0.00001
t=(1:100)/10
x1 = exp(-3.62*t)*(A*sin(52.75*t) + B*cos(52.75*t)) + exp(5.53*t)*
(C*sin(24.94*t) + D*cos(24.94*t)) + exp(0.024*t)*(E*sin(8.48*t) +
F*cos(8.48*t)) + G*sin(43.982*t) + H*cos(43.982*t)
% Plot results
subplot(1,1,1)
hold on;
plot(t',x1,'r')
ylabel('Position (m)')
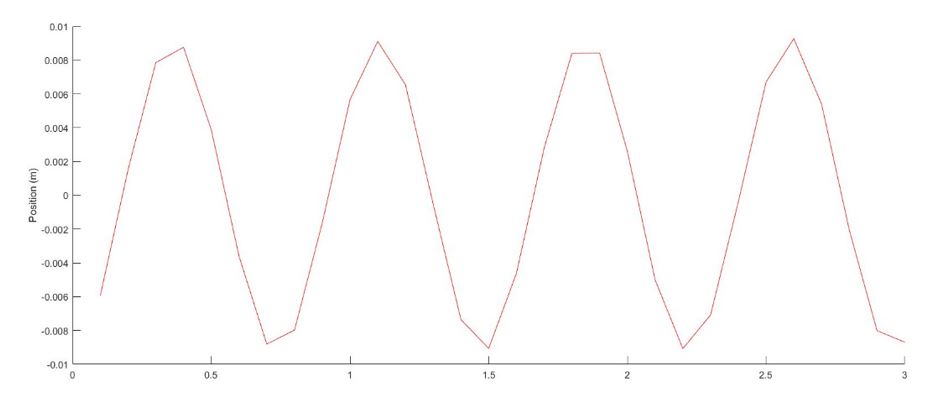
Gambar 5 Grafik respon posisi terhadap waktu
Grafik di atas menunjukan pengaruh getaran pada bagian bawah struktur pemodelan bangunan di mana perubahan arah gerak pada bagian bawah struktur membentuk pola sinusoidal yang menandakan adanya gerak bolak-balik pada struktur tersebut.
KESIMPULAN
Dalam permasalahan analisis gerak (perubahan arah, kecepatan dan percepatan) dapat dilakukan dengan metode lain berupa FES, namun pada artikel ini pemodelan FES belum dilakukan. Artikel ini hanya membahan mass-spring (MS) model yang terjadi pada suatu sistem pemodelan bangunan yang diberikan getaran. Sehingga dapat dilihat perilaku gerak bangunan sebagai respon dari adanya getaran yang diberikan.
REFERENSI
• Syaldiles Putri Indahdinata, Analisis Pengaruh Perubahan Cross Sectional Area Dan Posisi Peletakan Tuned Liquid Column Damper Terhadap Respon Dinamis Model Struktur Bangunan Bertingkat, Departemen Teknik Mesin FTI-ITS Surabaya, 2018.