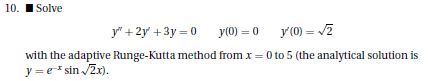Difference between revisions of "Omar Rayhan Khalif"

From ccitonlinewiki
Jump to: navigation, search
(→‎TUGAS 03 METNUM - PENGGUNAAN CFDSOFT DAN REGRESSI LINEAR PADA PYTHON)
 
(53 intermediate revisions by 5 users not shown)
Line 1: Line 1:
−
[[File:Omar.jpg|200px|thumb|left|alt text]]
+
[[File:600px-Omar.jpg|400px]]
−
'''Who am I?'''
+
== Who am I? ==
 +
 
  
 
My name is Omar, i was born March 9th, 2000 in Jakarta. Currently i'm a college student in University of Indonesia, majoring in Naval Architect and Marine Engineering, batch 2018. The reason i chose this major is because i want to make Indonesia's maritime sector become the best in Asia, even in the world, because Indonesia has so much potential in that sector that we haven't explored.
 
My name is Omar, i was born March 9th, 2000 in Jakarta. Currently i'm a college student in University of Indonesia, majoring in Naval Architect and Marine Engineering, batch 2018. The reason i chose this major is because i want to make Indonesia's maritime sector become the best in Asia, even in the world, because Indonesia has so much potential in that sector that we haven't explored.
 +
 +
== Coding Experience ==
 +
I was enrolled in a coding class during senior highschool, hosted by Zenius. But it was in the 10th grade, so i'm kind of forgot about all the formulas. But i had some experience in coding as well
 +
 +
 +
== TUGAS 01 METNUM ==
 +
Do a given F(x) formula :
 +
 +
1. Do it manually
 +
 +
2. And then do it with a computer (use software)
 +
 +
3. Give your analysis and comment about your answer
 +
 +
4. Upload it in air.eng,ui.ac.id
 +
 +
'''ANSWER'''
 +
 +
1. Manual Answer :
 +
 +
[[File:FUNGSI.png]]
 +
 +
Analysis :
 +
 +
First of all you just have to do some equation with the quadratic number, in this case a squared x. By making it (x+1)(x-1) After that you can eliminate the (x-1) with the same number below, so all you have left is the (x+1). So, for example if x is 1, then the answer is 2.
 +
 +
2. Software Answer (Ms. Excel) :
 +
 +
[[File:FUNGSI_1502.png|200x|thumb|left|Ms.Excel]]
 +
 +
Analysis :
 +
 +
Excel couldnt get the numbers right because, its divided is 0/0, which is an error because Excel substitute the amount of x, which is one, at the very beginning. So the top one is (1^2-1) when the bottom one is (1-1). There you get the result which is 0/0
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
== TUGAS 02.01 METNUM ==
 +
 +
Pada tugas kali ini saya memilih mengerjakan sebuah problem set 3.2 dari buku '''Numerical Methods in Engineering with Python 3''' no. 9, tentang pengerjaan Least Square melalui cara manual dan cara software menggunakan Python.
 +
 +
'''CARA MANUAL'''
 +
 +
[[File:CARAMANUAL.jpg|300px]]
 +
 +
Analisis :
 +
 +
Dengan cara manual, saya mengerjakan soal tersebut dengan menggunakan metode sigma x tidak sama dengan nol, sehingga rumus yang digunakan untuk mencari nilai b menjadi cukup panjang. Namun pada akhirnya, saya berhasil menemukan nilai b dan a tersebut, sehingga fungsi least square straight line/garis lurus berhasil ditemukan, yakni y=-6.045+9.38x
 +
 +
 +
'''CARA PYTHON'''
 +
 +
[[File:MAIN HALL.JPG|600px]]
 +
 +
Saya memasukan rumus yang terdapat dalam buku Metnum tentang Least Square, yang sesuai dengan soal yang saya pilih, namun angkanya saya sesuaikan dengan soal yang saya pilih.
 +
 +
[[File:POLY1.JPG|600px]]
 +
 +
[[File:POLY2.JPG|600px]]
 +
 +
[[File:POLY3.JPG|600px]]
 +
 +
Karena fungsi kuadrat f(x) = 0.1113 + 2.8512x 1.3683x^2 menghasilkan deviasi standar yang terkecil diantara 2 hasil lainnya, maka itu dapat dianggap sebagai yang paling fit untuk data. tapi perlu diingatkan, bahwasannya deviasi standar terkecil bukanlah pengukuran yang reliable untuk goodness of fit.
 +
 +
 +
== TUGAS 02.02 METNUM ==
 +
 +
'''SOAL INITIAL VALUE'''
 +
 +
 +
[[File:INITIALVALUE.JPG|600px]]
 +
 +
 +
'''PENYELESAIAN'''
 +
 +
 +
[[File:MAINHALL.JPG|600px]]
 +
 +
[[File:GRAFIKIV.JPG|600px]]
 +
 +
 +
 +
Analisis :
 +
 +
Untuk penyelesaian soal ODE tersebut, dengan menggunakan aplikasi coding python kita dapat langsung menemukan grafik dari ODE tersebut.
 +
 +
 +
== PRESENTASI PROGRESS BELAJAR ==
 +
 +
 +
[[File:PPT11.PNG|600px]]
 +
 +
[[File:PPT22.PNG|600px]]
 +
 +
[[File:PPT33.PNG|600px]]
 +
 +
[[File:PPT44.PNG|600px]]
 +
 +
[[File:PPT55.PNG|600px]]
 +
 +
 +
== HASIL ASISTENSI 1 (SELASA 25 FEB 2020) ==
 +
 +
[[File:PPT21.PNG|600px]]
 +
 +
[[File:PPT222.PNG|600px]]
 +
 +
[[File:PPT23.PNG|600px]]
 +
 +
[[File:PPT24.PNG|600px]]
 +
 +
[[File:PPT25.PNG|600px]]
 +
 +
 +
== TUGAS 03 METNUM - PENGGUNAAN CFDSOFT DAN REGRESSI LINEAR PADA PYTHON ==
 +
 +
Dengan menggunakan aplikasi/software CFDSOFT, kita dapat melihat simulasi optimasi kecepatan vs drag/resistance sebuah kapal selam. Saya memakai angka 11.5,12.5,13.5,14.5,15.5,16.5,17.5,18.5, dan 19.5 sebagai kecepatan (m/s) kapal selam tersebut untuk melihat hambatan yang dihasilkan. Berikut contoh simulasinya
 +
 +
[[File:Kapsel02.jpg|600px]]
 +
 +
Setelah itu, saya memasukan angka angka kecepatan yang telah disebutkan dalam aplikasi cfdsoft
 +
 +
[[File:Kapsel03.jpg|600px]]
 +
 +
Hingga munculah data data drag/hambatan yang dihasilkan ketika kapal tersebut menyentuh tiap tiap angka kecepatan tersebut, mulai dari 11.5 sampai 19.5 mempunyai nilai drag/resistansi tersendiri. angka angka tersebut adalah sebagai berikut : 281.613,337.896,399.319,465.87,537.55,614.377,696.317,783.405,875.641,972.992
 +
 +
Kemudian, kita memasukan angka angka tersebut (kecepatan dan hambatan) di python, dengan array x sebagai kecepatan dan array y sebagai hambatan yang dihasilkan. Berikut adalah kalkulasinya :
 +
 +
[[File:Kapsel01.PNG|600px]]
 +
 +
Maka, dihasilkanlah persamaan regressi linear dengan x1 = 2.56708712, x2 = -0.19307424 dan x3 = 0.62104261]
 +
 +
Sekian dan terima kasih.

Latest revision as of 03:15, 6 March 2020

600px-Omar.jpg

Who am I?

My name is Omar, i was born March 9th, 2000 in Jakarta. Currently i'm a college student in University of Indonesia, majoring in Naval Architect and Marine Engineering, batch 2018. The reason i chose this major is because i want to make Indonesia's maritime sector become the best in Asia, even in the world, because Indonesia has so much potential in that sector that we haven't explored.

Coding Experience

I was enrolled in a coding class during senior highschool, hosted by Zenius. But it was in the 10th grade, so i'm kind of forgot about all the formulas. But i had some experience in coding as well


TUGAS 01 METNUM

Do a given F(x) formula :

1. Do it manually

2. And then do it with a computer (use software)

3. Give your analysis and comment about your answer

4. Upload it in air.eng,ui.ac.id

ANSWER

1. Manual Answer :

FUNGSI.png

Analysis :

First of all you just have to do some equation with the quadratic number, in this case a squared x. By making it (x+1)(x-1) After that you can eliminate the (x-1) with the same number below, so all you have left is the (x+1). So, for example if x is 1, then the answer is 2.

2. Software Answer (Ms. Excel) :

Ms.Excel

Analysis :

Excel couldnt get the numbers right because, its divided is 0/0, which is an error because Excel substitute the amount of x, which is one, at the very beginning. So the top one is (1^2-1) when the bottom one is (1-1). There you get the result which is 0/0






TUGAS 02.01 METNUM

Pada tugas kali ini saya memilih mengerjakan sebuah problem set 3.2 dari buku Numerical Methods in Engineering with Python 3 no. 9, tentang pengerjaan Least Square melalui cara manual dan cara software menggunakan Python.

CARA MANUAL

CARAMANUAL.jpg

Analisis :

Dengan cara manual, saya mengerjakan soal tersebut dengan menggunakan metode sigma x tidak sama dengan nol, sehingga rumus yang digunakan untuk mencari nilai b menjadi cukup panjang. Namun pada akhirnya, saya berhasil menemukan nilai b dan a tersebut, sehingga fungsi least square straight line/garis lurus berhasil ditemukan, yakni y=-6.045+9.38x


CARA PYTHON

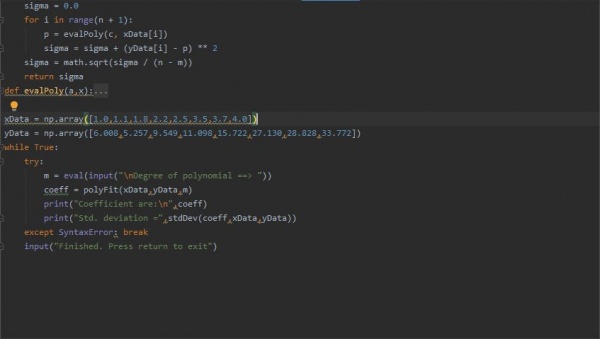
MAIN HALL.JPG

Saya memasukan rumus yang terdapat dalam buku Metnum tentang Least Square, yang sesuai dengan soal yang saya pilih, namun angkanya saya sesuaikan dengan soal yang saya pilih.

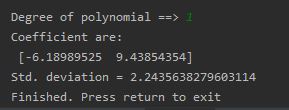
POLY1.JPG

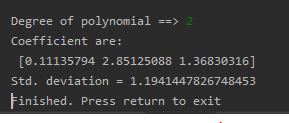
POLY2.JPG

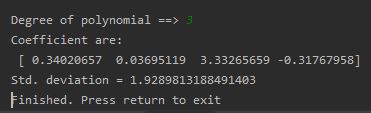
POLY3.JPG

Karena fungsi kuadrat f(x) = 0.1113 + 2.8512x 1.3683x^2 menghasilkan deviasi standar yang terkecil diantara 2 hasil lainnya, maka itu dapat dianggap sebagai yang paling fit untuk data. tapi perlu diingatkan, bahwasannya deviasi standar terkecil bukanlah pengukuran yang reliable untuk goodness of fit.


TUGAS 02.02 METNUM

SOAL INITIAL VALUE


INITIALVALUE.JPG


PENYELESAIAN


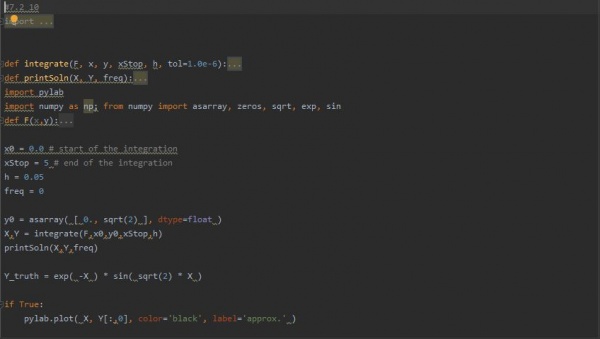
MAINHALL.JPG

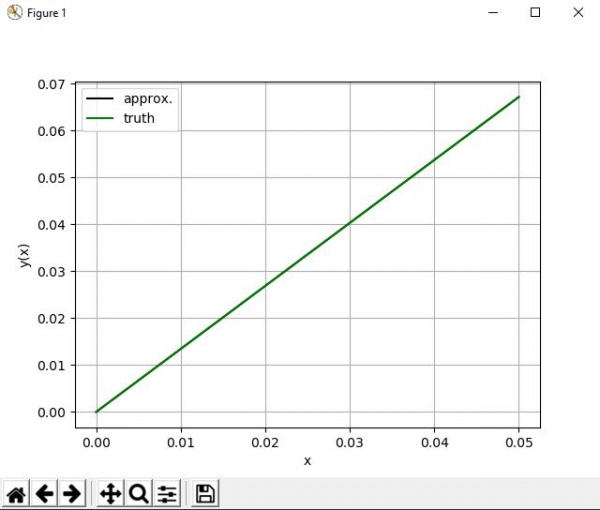
GRAFIKIV.JPG


Analisis :

Untuk penyelesaian soal ODE tersebut, dengan menggunakan aplikasi coding python kita dapat langsung menemukan grafik dari ODE tersebut.


PRESENTASI PROGRESS BELAJAR

PPT11.PNG

PPT22.PNG

PPT33.PNG

PPT44.PNG

PPT55.PNG


HASIL ASISTENSI 1 (SELASA 25 FEB 2020)

PPT21.PNG

PPT222.PNG

PPT23.PNG

PPT24.PNG

PPT25.PNG


TUGAS 03 METNUM - PENGGUNAAN CFDSOFT DAN REGRESSI LINEAR PADA PYTHON

Dengan menggunakan aplikasi/software CFDSOFT, kita dapat melihat simulasi optimasi kecepatan vs drag/resistance sebuah kapal selam. Saya memakai angka 11.5,12.5,13.5,14.5,15.5,16.5,17.5,18.5, dan 19.5 sebagai kecepatan (m/s) kapal selam tersebut untuk melihat hambatan yang dihasilkan. Berikut contoh simulasinya

Kapsel02.jpg

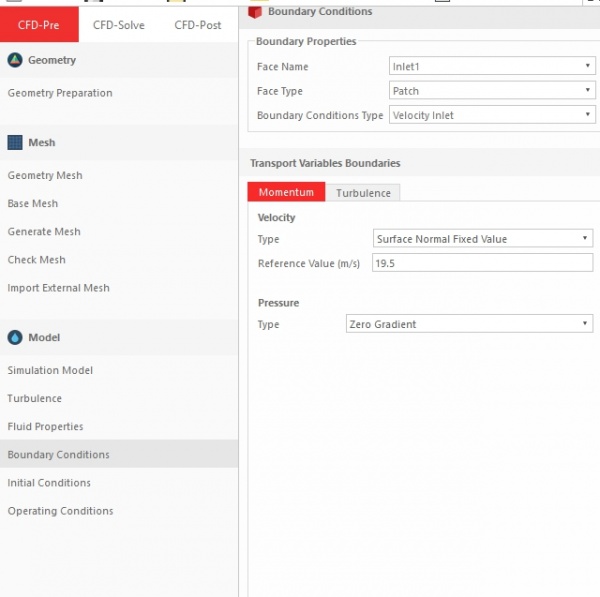
Setelah itu, saya memasukan angka angka kecepatan yang telah disebutkan dalam aplikasi cfdsoft

Kapsel03.jpg

Hingga munculah data data drag/hambatan yang dihasilkan ketika kapal tersebut menyentuh tiap tiap angka kecepatan tersebut, mulai dari 11.5 sampai 19.5 mempunyai nilai drag/resistansi tersendiri. angka angka tersebut adalah sebagai berikut : 281.613,337.896,399.319,465.87,537.55,614.377,696.317,783.405,875.641,972.992

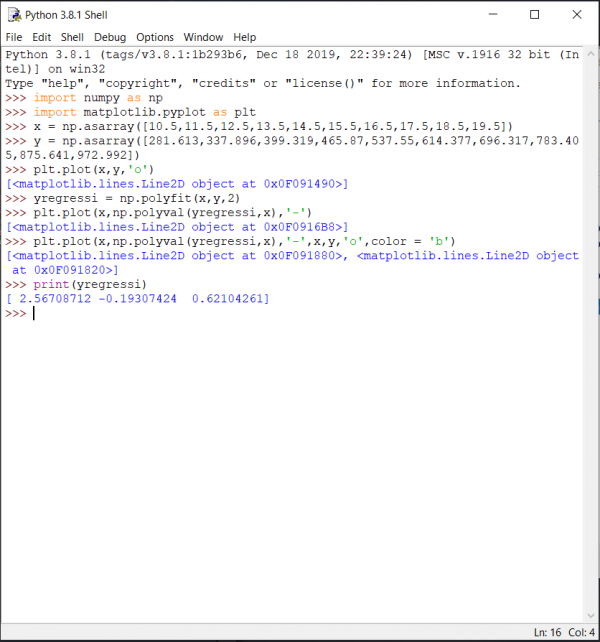
Kemudian, kita memasukan angka angka tersebut (kecepatan dan hambatan) di python, dengan array x sebagai kecepatan dan array y sebagai hambatan yang dihasilkan. Berikut adalah kalkulasinya :

Kapsel01.PNG

Maka, dihasilkanlah persamaan regressi linear dengan x1 = 2.56708712, x2 = -0.19307424 dan x3 = 0.62104261]

Sekian dan terima kasih.

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Omar_Rayhan_Khalif&oldid=26209"