Difference between revisions of "Benarido Amri"
| Line 52: | Line 52: | ||
We use the the same for loop to calculate all the necessary variables, such as the weight and deflection. Here we have the equations used to calculate the variables below : | We use the the same for loop to calculate all the necessary variables, such as the weight and deflection. Here we have the equations used to calculate the variables below : | ||
| − | [[File:Equation_Formulas.png|400px|thumb|right| | + | [[File:Equation_Formulas.png|400px|thumb|right|Formulas for calculation]] |
To calculate the deflection, only the main cylinder is calculated with the assumption of the load situated at the middle of the cylinder. This is to simulate an impact at the center of the tank while the tank is empty and thus there is no pressure acting on the inside of the cylinder. This assumption may not be accurate, however since I couldn't find the appropriate formula for the shape of the whole storage tank, we will need to go by this assumption. | To calculate the deflection, only the main cylinder is calculated with the assumption of the load situated at the middle of the cylinder. This is to simulate an impact at the center of the tank while the tank is empty and thus there is no pressure acting on the inside of the cylinder. This assumption may not be accurate, however since I couldn't find the appropriate formula for the shape of the whole storage tank, we will need to go by this assumption. | ||
| Line 64: | Line 64: | ||
E = 193e9 # Modulus of elasticity for AISI 304 | E = 193e9 # Modulus of elasticity for AISI 304 | ||
F = 100000 # Simulated force | F = 100000 # Simulated force | ||
| − | |||
results1 = [] | results1 = [] | ||
results2 = [] | results2 = [] | ||
| Line 77: | Line 76: | ||
results2.append(deflection) | results2.append(deflection) | ||
results3.append(thickness) | results3.append(thickness) | ||
| − | |||
''' | ''' | ||
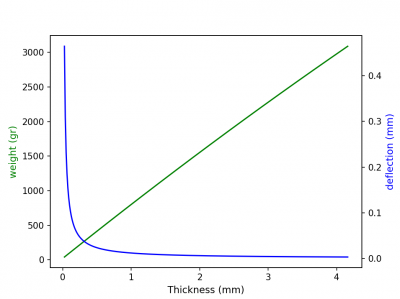
| − | From the code above we can then plot the values into a graph | + | From the code above we can then plot the values into a graph as shown below : |
| + | |||
| + | [[File:Weight_Deflection_Graph.png|400px|thumb|left|Graph result]] | ||
| + | |||
| + | From the graph by finding the intersection between the two lines, we can find the best wall thickness, which is around '''0.312 mm.''' With a weight of 266.7 gram and a deflection value of 0.03775 mm. | ||
| + | |||
| + | ==== Conclusion and Evaluation ==== | ||
| + | Based on the result above, the ideal thickness when considering only the weight and the deflection factor would be 0.312 mm, however we must also consider other factors when designing or manufacturing storage tank. Although the result of the wall thickness seems to be very thin, this is probably due to the assumptions of taking only the wall cylinder. | ||
| + | |||
| + | Other interesting note that we can take from this procedure is that it is relatively simple to do, and can be done for many other parameters that we wanted to know, the accuracy however may not be as accurate as some other methods. | ||
Revision as of 21:13, 5 June 2023
Contents
Introduction
- Full Name : Benarido Amri
- NPM : 2106718230
- Major : Mechanical Engineering
- Email : benarido.amri@ui.ac.id
- Lecturer : Dr. Ahmad Indra Siswantara
Assalamualaikum Wr. Wb.
My name is Benarido Amri currently studying Mechanical Engineering at Universitas Indonesia. this page would be a way for me to update the progress of learning Numerical Method.
Design Project
Pressurized Hydrogen Storage
Hydrogen can be a great alternative for conventional electric vehicle energy source, since it can provide many benefits such as less charge time and cleaner environmental waste. However, the problem we face with hydrogen is the safety concerns regarding its storage method, even though hydrogen is generally safe under normal pressure, it can be a major safety issue when stored at such a high pressure -which is how the hydrogen will be stored in a EVs-, upon accident many worried that the hydrogen could explode, or catch fire.
In this Numerical Method class, our ultimate goal would be to find a way to safely contain pressurized hydrogen. Although we are going to focus on a much smaller case and less pressure. With the specifications being 1 liter of hydrogen pressurized to 8 bar.
Optimization Consideration
We were tasked of designing a pressurized hydrogen storage tank which can hold up to 1 liter of 8 bar hydrogen which costs less than Rp. 500 000. For the optimization, we wanted to optimize the cost without sacrificing the performance such as safety, and reliability.
Material Selection
The current material selection for the storage is generally made of metal such as austenitic stainless steel (AISI 316 and AISI 304). This is because hydrogen storage must have very high tensile strength, low density, and doesn't react with hydrogen.
Optimization Objective
- Design Variables = Thickness, weight, and deflection.
- Objective Function = To find the most suitable wall thickness when considering the trade off between weight and strength (deflection) of the storage tank.
- Constraints = The storage tank must be able to fit within a space of 5.8325 cm x 5.8325 cm x 11.0234 cm rectangular box shape or around 1.5 L of volume. And must be able to hold a minimum of 1 L of hydrogen.
For the storage tank project, I will attempt to optimize the wall thickness of the tank by considering the weight and deflection. Weight can be a crucial factor especially when the storage tank is for applications that needs to be mobile and light. However if we were to use the same material, reducing weight can have an effect on its strength, one aspect of strength compromised is its ability to resist deflection when given a force.
The optimization process is done by using a graph to find the intersection point between deflection and weight. Due to the many formulas and equations involved, we can simplify the calculation by using a code such as python or MATLAB. In my case, I will be using a python programming language.
Design
Before we can calculate the weight and deflection, we need to define our material, shape, and also size. The shape of the tank can be divided into 2 basic geometry, the main cylinder and the cap on both sides. The total dimension of the storage tank is 11.0234 cm in length and has a radius of 5.8325 cm. The main cylinder has a height of 5.1909 cm and a radius of 5.8325 cm, while the cap has a radius of 5.8325, a height of 2.91625 cm, and a fillet radius equal to half of the main cylinder radius. These description can be seen on the image below.
The size and shape is taken from Jiddan's work on the ideal radius to height ratio of such storage tank, determining the ideal ratio to be around 1.89.
For the material, from the paper "Materials for hydrogen storage" by Andreas Zuttel, they stated that the common material for hydrogen storage is stainless steel AISI 316 and AISI 304, which is an austenitic type steel. So for the design project I decide to use the stainless steel AISI 304. AISI 304 is quite a common material and it is often used for many applications outside of the storage tank.
Coding
Due to the many variables and formulas involved, coding can be a great tool to help us calculate all the numbers for the graph. The code starts with importing the necessary modules from the library. The next step would be to define the known parameters, in this case the total height, outer radius, cylinder height, total volume, modulus of elasticity, and the simulated force.
We use the the same for loop to calculate all the necessary variables, such as the weight and deflection. Here we have the equations used to calculate the variables below :
To calculate the deflection, only the main cylinder is calculated with the assumption of the load situated at the middle of the cylinder. This is to simulate an impact at the center of the tank while the tank is empty and thus there is no pressure acting on the inside of the cylinder. This assumption may not be accurate, however since I couldn't find the appropriate formula for the shape of the whole storage tank, we will need to go by this assumption.
h_t = 11.0234 # Total height
r_o = 5.8325 # Outer radius
h = h_t - r_o # Cylinder height
V_t = 1454.8338 # Total volume
E = 193e9 # Modulus of elasticity for AISI 304
F = 100000 # Simulated force
results1 = []
results2 = []
results3 = []
for r_i in np.arange(5, r_o - 0.0025, 0.0025):
fluid_volume = ((4*(r_i**2)) * h_t) - (pi * (r_i**2) * (4/3 * 1/64 * r_i + 1/16 * h))
material_volume = V_t - fluid_volume
weight = material_volume * 8 # Weight is the volume times the density of material (8 gr/cm^3)
thickness = (r_o - r_i)/2 * 10 # Calculating the thickness in (mm)
deflection = ((F * (h_t/100)**3)/(48 * E * (pi/64 * (((2 * r_o/100)**4)-((2 * r_i/100)**4))))) * 1000 # Calculation of the deflection converted to (mm)
results1.append(weight)
results2.append(deflection)
results3.append(thickness)
From the code above we can then plot the values into a graph as shown below :
From the graph by finding the intersection between the two lines, we can find the best wall thickness, which is around 0.312 mm. With a weight of 266.7 gram and a deflection value of 0.03775 mm.
Conclusion and Evaluation
Based on the result above, the ideal thickness when considering only the weight and the deflection factor would be 0.312 mm, however we must also consider other factors when designing or manufacturing storage tank. Although the result of the wall thickness seems to be very thin, this is probably due to the assumptions of taking only the wall cylinder.
Other interesting note that we can take from this procedure is that it is relatively simple to do, and can be done for many other parameters that we wanted to know, the accuracy however may not be as accurate as some other methods.