Difference between revisions of "Tri Aji Setyawan"
(→MINGGU KE 3) |
(→UJIAN AKHIR SEMESTER) |
||
| (41 intermediate revisions by the same user not shown) | |||
| Line 199: | Line 199: | ||
menyelesaikan 2 soal dengan open modelica yang berhubungan dengan engineering | menyelesaikan 2 soal dengan open modelica yang berhubungan dengan engineering | ||
| + | |||
| + | [[File:7776.jpg|600px|center]] | ||
| + | |||
| Line 204: | Line 207: | ||
<syntaxhighlight lang="modelica"> | <syntaxhighlight lang="modelica"> | ||
| − | problem 1 | + | problem 1 ( pada example 3.1) |
*model Trusses | *model Trusses | ||
| Line 324: | Line 327: | ||
Grafik Reaction forces | Grafik Reaction forces | ||
| − | [[File: | + | [[File:1 Reaction Forces.jpg|600px|center]] |
| + | |||
Grafik Diplacement | Grafik Diplacement | ||
| − | [[File:Diplacement.jpg|600px|center]] | + | [[File:1 Diplacement.jpg|600px|center]] |
| + | |||
| + | |||
| + | problem 2 ( PR NO 4 ) | ||
| − | + | [[File:709714.jpg|600px|center]] | |
<syntaxhighlight lang="modelica"> | <syntaxhighlight lang="modelica"> | ||
| − | *class | + | *class MetodeTrusses |
parameter Integer N=8; //Global matrice = 2*points connected | parameter Integer N=8; //Global matrice = 2*points connected | ||
parameter Real A=0.001; //Area m2 | parameter Real A=0.001; //Area m2 | ||
| Line 437: | Line 444: | ||
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | ||
| − | end | + | end MetodeTrusses; |
</syntaxhighlight> | </syntaxhighlight> | ||
Grafik Reaction Process | Grafik Reaction Process | ||
| − | [[File:Reaction | + | [[File:2 Reaction Forces.jpg|600px|center]] |
Grafik Diplacement | Grafik Diplacement | ||
| − | [[File:Diplacement | + | [[File:2 Diplacement.jpg|600px|center]] |
| Line 583: | Line 590: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | == MINGGU KE 4 == | ||
| + | |||
| + | Kuis pada hari rabu tanggal 2 desember 2020 | ||
| + | |||
| + | membuat diagram class dan flowchart dari fungsi yang telah dibuat josiah | ||
| + | |||
| + | |||
| + | == KUIS DIAGRAM CLASS DAN FLOWCHART == | ||
| + | |||
| + | [[File:710706.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | == Tugas Minggu ke 4 == | ||
| + | |||
| + | Pada tugas ke 4 kali ini , kami diberikan soal untuk menyelesaikan sebuah permasalahan mengenai space truss dengan membuat flowchart, diagram class, dan coding modelicanya. | ||
| + | |||
| + | [[File:719897.jpg|600px|center]] | ||
| + | |||
| + | jawab : | ||
| + | |||
| + | Pertama tama saya membuat flowchart dan diagram class. lalu saya membuat free body diagram dari sistem dan mencari data-data yang dibutuhkan. | ||
| + | |||
| + | [[File:720102.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | Class Diagram | ||
| + | |||
| + | [[File:720095.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | Flowchart | ||
| + | |||
| + | |||
| + | [[File:720104.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | Setelah data-data sudah didapatkan lalu diproses ke dalam OpenModelica menggunakan referensi coding A. M. Fahmi. | ||
| + | |||
| + | Saya mencari k tiap element terlebih dahulu menggunakan rumus k=AE/L. Setelah itu bisa mencari nilai Ke. | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | function StiffnessMatrixElement | ||
| + | |||
| + | input Real [:,9] inisiasi_mat; | ||
| + | output Real [size(inisiasi_mat,1),6,6] Ke_mat; | ||
| + | |||
| + | protected | ||
| + | Real cos_x; | ||
| + | Real cos_y; | ||
| + | Real cos_z; | ||
| + | Real [6] StiffTrig; | ||
| + | Real [6,6] StiffTrans; | ||
| + | Real [size(inisiasi_mat,1)] k_vec; | ||
| + | |||
| + | algorithm | ||
| + | k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)}; | ||
| + | |||
| + | // Finding stiffness matrix of each element member | ||
| + | for i in 1:size(inisiasi_mat,1) loop | ||
| + | |||
| + | // Clearing the matrices | ||
| + | StiffTrig := zeros(6); | ||
| + | StiffTrans := zeros(6,6); | ||
| + | |||
| + | // Converting degrees to radians | ||
| + | cos_x := inisiasi_mat[i,4]; | ||
| + | cos_y := inisiasi_mat[i,5]; | ||
| + | cos_z := inisiasi_mat[i,6]; | ||
| + | |||
| + | // {cos^2, sin^2, sincos} | ||
| + | StiffTrig := {(cos_x)^2, | ||
| + | (cos_y)^2, | ||
| + | (cos_z)^2, | ||
| + | (cos_x*cos_y), | ||
| + | (cos_x*cos_z), | ||
| + | (cos_y*cos_z)}; | ||
| + | |||
| + | // Construct stiffness transformation matrix | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5]; | ||
| + | StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6]; | ||
| + | StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5]; | ||
| + | -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6]; | ||
| + | -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]]; | ||
| + | |||
| + | // Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat | ||
| + | for m in 1:6 loop | ||
| + | for n in 1:6 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end for; | ||
| + | end StiffnessMatrixElement; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Membuat stiffness matrix global | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | |||
| + | |||
| + | function StiffnessMatrixGlobal | ||
| + | input Integer [:,2] n; | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,6,6] Ke_mat; | ||
| + | output Real [y,x,x] Kg_mat; | ||
| + | |||
| + | algorithm | ||
| + | for i in 1:y loop | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | Kg_mat[i,a,b]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:y loop | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; | ||
| + | |||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end StiffnessMatrixGlobal; | ||
| + | |||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Semua stiffness matrix global dijumlahkan dan didapatkan sum stiffness matrix global. | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | |||
| + | function SumStiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,x,x] Kg_mat; | ||
| + | output Real [x,x] KgTot_mat; | ||
| + | |||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end SumStiffnessMatrixGlobal; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | menentukan boundaries pada sum stiffness matrix global. | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | |||
| + | |||
| + | function BoundaryStiffnessMatrixGlobal | ||
| + | input Integer x; | ||
| + | input Integer z; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Integer[z] Boundary_met; | ||
| + | output Real [x,x] KgB_met; | ||
| + | |||
| + | algorithm | ||
| + | for a in 1:x loop | ||
| + | for b in 1:x loop | ||
| + | KgB_met[a,b] := KgTot_met [a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:x loop | ||
| + | for a in 1:z loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*(Boundary_met[a])-b,i]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | for a in 1:z loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end BoundaryStiffnessMatrixGlobal; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | |||
| + | Untuk mencari nilai displacement (U) lainnya digunakan eliminasi Gauss Jordan dengan persamaan XU=F. Dimana X adalah stiffness matrix global yang sudah ditentukan boundarynya. | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | function GaussJordan | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgB_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] U_met; | ||
| + | |||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | |||
| + | for i in 1:x loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end GaussJordan; | ||
| + | |||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | kemudian mencari reaction menggunakan persamaan R=Kg*U - F. | ||
| + | |||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | |||
| + | function ReactionForce | ||
| + | input Integer x; | ||
| + | input Real [x,x] KgTot_met; | ||
| + | input Real [x] U_met; | ||
| + | input Real [x] load_met; | ||
| + | output Real [x] R_met; | ||
| + | |||
| + | algorithm | ||
| + | R_met := (KgTot_met*U_met)-load_met; | ||
| + | end ReactionForce; | ||
| + | |||
| + | |||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Selanjutnya, membuat sebuah Class untuk memanggil fungsi-fungsi diatas agar bisa melihat nilai U dan R. | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | class truss | ||
| + | parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5; | ||
| + | 2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5; | ||
| + | 3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5]; | ||
| + | |||
| + | parameter Integer [:,2] node = [1, 2; | ||
| + | 1, 3; | ||
| + | 1, 4]; | ||
| + | |||
| + | parameter Integer y = size(node,1); | ||
| + | |||
| + | parameter Integer x = 3*(size(node_load,1)); | ||
| + | |||
| + | parameter Integer z = size(Boundary,1); | ||
| + | |||
| + | parameter Integer [:] Boundary = {2,3,4}; | ||
| + | |||
| + | parameter Real [:,4] node_load = [1, 0, -5000, 0; | ||
| + | 2, 0, 0, 0; | ||
| + | 3, 0, 0, 0; | ||
| + | 4, 0, 0, 0]; | ||
| + | |||
| + | parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}; | ||
| + | |||
| + | Real [y] k; | ||
| + | |||
| + | Real [y,6,6] Ke; | ||
| + | |||
| + | Real [y,x,x] Kg; | ||
| + | |||
| + | Real [x,x] KgTot; | ||
| + | |||
| + | Real [x,x] KgB; | ||
| + | |||
| + | Real [x] U; | ||
| + | |||
| + | Real [x] R; | ||
| + | |||
| + | equation | ||
| + | k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y}; | ||
| + | |||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | |||
| + | Kg = StiffnessMatrixGlobal(node, x, y, Ke); | ||
| + | |||
| + | KgTot = SumStiffnessMatrixGlobal(x, y, Kg); | ||
| + | |||
| + | KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); | ||
| + | |||
| + | U = GaussJordan(x, KgB, load); | ||
| + | |||
| + | R = ReactionForce(x, KgTot, U, load); | ||
| + | |||
| + | end truss; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | hasil dari U dan R | ||
| + | |||
| + | |||
| + | [[File:Hasil triaji.jpg|600px|center]] | ||
| + | |||
| + | grafik | ||
| + | |||
| + | |||
| + | [[File:MessageImage 1607507360567.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | video penjelasan terkait penyelesaian soal no 8 | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <youtube width="200" height="100">https://youtu.be/HOAG88KMp_g</youtube> | ||
| + | </div> | ||
| + | |||
| + | == Aplikasi Metode Numerik dalam Kasus Optimasi == | ||
| + | |||
| + | Pada minggu ke 6 , kami mempelajari mengenai optimasi. sebelum kuliah dimulai, bu chandra memberikan penjelasan singkat mengenai optimasi dengan menggunakan bracket. Di akhir video , kami diperintahkan untuk mencoba perhitungan optimasi yang ada di video. | ||
| + | |||
| + | Membuat model untuk memanggil fungsi | ||
| + | |||
| + | [[File:MODEL.jpg|600px|center]] | ||
| + | |||
| + | Fungsi yang akan di panggil | ||
| + | |||
| + | [[File:Fungsi.jpg|600px|center]] | ||
| + | |||
| + | Hasil yang diperoleh | ||
| + | |||
| + | |||
| + | [[File:Hasil Optimasi.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | == TUGAS BESAR METNUM == | ||
| + | |||
| + | Pada tugas besar ini, kami diperimtahkan untuk mendesain rangka dengan menggunakan optimasi. | ||
| + | |||
| + | [[File:Soal triaji1.jpg|600px|center]] | ||
| + | [[File:Diketahui triaji 2.jpg|600px|center]] | ||
| + | |||
| + | Dari soal tersebut kita diperintahkan untuk mendesain rangka batang dengan harga terjangkau dan optimal untuk fungsinya. | ||
| + | |||
| + | Yang perlu kita cari adalah Harga, Material yang digunakan, cross section Dilakukan dengan metode optimasi dan membentuk curve fitting pada variabel harga | ||
| + | |||
| + | Asumsi yang digunakan dalam perhitungan ini : | ||
| + | *Beban akan terdistribusi hanya pada node (karena bersifat trusses). | ||
| + | *Safety factor minimal bernilai 2. | ||
| + | *Batas displacement 0,001 m sebelum buckling (pada truss paling atas). | ||
| + | *Ketinggian trusses pada tiap lantai sama yaitu 0,6 m. | ||
| + | |||
| + | Untuk jenis material yang sama: | ||
| + | *Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu SS304 . | ||
| + | *Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal. | ||
| + | *Membuat rasio antara safety factor dengan harga total. | ||
| + | *Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting. | ||
| + | *Melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | Untuk area penampang yang sama: | ||
| + | *Mencari harga untuk 3 jenis material dengan area penampang yang sama yaitu 171 mm^2. | ||
| + | *Mengitung nilai safety factor pada 3 jenis batang dengan coding awal. | ||
| + | *Membuat rasio antara safety factor dengan harga total. | ||
| + | *Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting. | ||
| + | *Melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | Kemudian , saya akan menggunakan coding sebagai berikut untuk melakukan perhitugnan sehingga didapatkan reaction force , stress , displacement , dan safety factor ( yield / stress ). | ||
| + | |||
| + | ''' Coding Yang akan digunakan ''' | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | model Trusses_3D_Tugas_Besar_Safety | ||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000201; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) | ||
| + | parameter Real Elas=200e9; //Elasticity SS304 Stainless Steel (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | |||
| + | end Trusses_3D_Tugas_Besar_Safety; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | ''' Membuat Kurva Curve Fitting ''' | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | ''' Untuk Optimasi Golden Section ''' | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | model Opt_Gold | ||
| + | |||
| + | parameter Real xd[:]; | ||
| + | parameter Real yd[size(xd,1)]; | ||
| + | parameter Real xlo=87e-6; | ||
| + | parameter Real xhi=504e-6; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Opt_Gold; | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | Material Tetap | ||
| + | |||
| + | [[File:Tabel Material Locked.jpg|600px|center]] | ||
| + | |||
| + | Hasil Optimasi : | ||
| + | |||
| + | [[File:LUAS AREA OPTIMUM.jpg|600px|center]] | ||
| + | |||
| + | Nilai luas area penampang optimum untuk material SS304 adalah 0.000423422m^2. | ||
| + | |||
| + | |||
| + | Luas Truss Tetap | ||
| + | |||
| + | [[File:Tabel Area Locked.jpg|600px|center]] | ||
| + | |||
| + | Hasil Optimasi : | ||
| + | |||
| + | [[File:MessageImage 1609924268406.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | Material optimum yang dapat digunakan untuk luas penampang 171mm^2 adalah material dengan nilai elastisitas sebesar 1.9697x10^11Pa, yaitu material SS304. | ||
| + | |||
| + | == UJIAN AKHIR SEMESTER == | ||
| + | |||
| + | Jawaban Uas | ||
| + | |||
| + | [[File:Uas no 1 dan 2.jpg|600px|center]] | ||
| + | |||
| + | [[File:Uas no 3.jpg|600px|center]] | ||
| + | |||
| + | [[File:Uas no 4 dan 5.jpg|600px|center]] | ||
| + | |||
| + | [[File:Uas no 6 dan 7.jpg|600px|center]] | ||
| + | |||
| + | |||
| + | '''coding yang akan digunakan ''' | ||
| + | |||
| + | <syntaxhighlight lang="modelica"> | ||
| + | |||
| + | |||
| + | model Uas_MetodeNumerik | ||
| + | //define initial variable | ||
| + | parameter Integer Points=4; //Number of Points | ||
| + | parameter Integer Trusses=3; //Number of Trusses | ||
| + | parameter Real Yield=214e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.16; //Area Block Profile (0.4 * 0.4) (m2) | ||
| + | parameter Real Elas=207e9; //Elasticity SS 304 (Pa) | ||
| + | parameter Real Volume=1135; //m3 from 200000 gallons | ||
| + | parameter Real rho=1000; //kg/m3 | ||
| + | |||
| + | parameter Real W=Volume*rho*9.81; | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[Trusses,2]=[1,2; | ||
| + | 2,3; | ||
| + | 2,4]; | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[Points,3]=[0,37,0; | ||
| + | 0,12,0; | ||
| + | -16,0,0; | ||
| + | 16,0,0]; | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,-W,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0}; | ||
| + | |||
| + | //define boundary | ||
| + | parameter Integer b[:]={3,4}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b); | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for i in boundary loop | ||
| + | for j in 1:N loop | ||
| + | G[i,j]:=id[i,j]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Uas_MetodeNumerik; | ||
| + | |||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | [[File:Hasil Uas.jpg|600px|center]] | ||
Latest revision as of 18:28, 14 January 2021
Contents
[hide]Biodata
Tri Aji Setyawan 1906301324
Saya merupakan mahasiswa teknik mesin UI angkatan 2019. saya menyukai teknik mesin karena tertarik pada bidang manufaktur dan karena teknik mesin sendiri memiliki prospek kerja yang luas. hal yang saya pelajari sebelum uts ini adalah mengenai turunan numerik, deret mclaurin , interpolasi, regresi, pengertian dari metode numerik, pseucode.
MINGGU KE 1
- Tujuan mempelajari metode numerik
- 1. matching dengan tujuan belajar: memahami konsep dan prinsip dasar di dalam metnum. contoh persamaan aljabar, algorithma, pencocokan kurva, persamaan diferensial parsial.
- 2. dapat menerapkan pemahaman terhadap konsep di dalam permodelan numerik ( pengaplikasian metode numerik )
- 3. mampu menerapkan metnum di dalam persoalan keteknikan.
- 4. untuk mencapai poin 1,2,3, yaitu dengan cara moral value (adab). untuk menambah nilai tambah / adabsehingga kita menjadi orang yang lebih beradab
TUGAS 1
Pada pertemuan sebelumnya , saya mendapatkan tugas untuk membuat video terkait penggunaan aplikasi open modelica
MINGGU KE 2
perbedaan openmodelica dengan python , open modelicca lebih ke bahasa permodelan sedangkan python hanya bahasa cpoding. kelebihan dari open modelicca yaitu :
- menggunakan bahasa permodelan yang cocok untuk seorang engineer
- proses perhitungan lebih cepat
- pengguna aplikasi openmodelica cukup banyak penggunanya, dan termasuk open teknologi (free).
pada minggu kedua, saya mempelajari mengenai cara memanggil fungsi dalam suatu kelas tertentu
Tugas 2
mengaplikasikan penggunaan fitur function dan class pada open modelica. Membuat sebuah fungsi berupa persamaan aljabar simultan dengan variabel array kemudian membuat class untuk memanggil fungsi tersebut. Persamaan aljabar simultan adalah sebuah persoalan matematika yang kompleks sehingga penyelesaian perlu dengan menggunakan tools, agar dapat dibuat lebih sederhana.
pada tugas kali ini saya mencoba menyelesaikan suatu soal sistem persamaan linier menggunakan metode gauss
MINGGU KE 3
Pada pertemuan ketiga, Pak Dai menjelaskan mengenai tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik
- 1. Computation Fluid Dynamics (CFD)
- 2. Finite Element Analysis
- 3. Metode Stokastik.
Pak Dai kemudian menugaskan untuk membuat fungsi mengenai gauss jordan. kemudian dijelaskan oleh cristo dengan fungsi sebagai berikut :
// Gauss-Jordan Algorithm // Transforms input matrix A into reduced row echelon form matrix B // Christopher S.E. November 2020 input Real [:,:] A; // An augmented matrix of m*n output Real [:,:] B; // Output matrix in reduced row echelon form // Local variables
protected Integer h = 1; // Initialize pivot row Integer k = 1; // Initialize pivot column Integer m = size(A,1); // Number of rows in matrix Integer n = size(A,2); // Number of columns in matrix Integer c = 0; // Index counter Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column; // Vector containing pivot column data Real [:] pivot_row; // Vector containing backwards pivot row data Real [:,:] temp_array; // Stores matrix data when switching rows Real r; // Ratio value used for row operations
// Limit to handle floating point errors Real float_error = 10e-10;
algorithm
// Transfer input matrix A into variable B B := A;
while h <= m and k <= n loop
// Dealing with floating point errors
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
// Finding the pivot
pivot_column := {B[i,h] for i in h:m};
// Get position index of lowest row with greatest pivot number
c:= h-1;
for element in pivot_column loop
c := c+1;
if abs(element) == max(abs(pivot_column)) then
max_row := c;
end if;
end for;
// No pivot in this column, move on to next column
if B[max_row, k] == 0 then
k := k+1;
else
// Swap Rows h <-> max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
// Divide pivot row by pivot number
B[h] := B[h]/B[h,k];
// For all rows below the pivot
for i in (h+1):m loop
// Store the ratio of the row to the pivot
r := B[i,k] / B[h,k];
// Set lower part of pivot column to zero
B[i,k] := 0;
// Operations on the remaining row elements
for j in (k+1):n loop
B[i,j] := B[i,j] - B[h,j] * r;
end for;
end for;
// Move on to next pivot row and column
h := h+1;
k := k+1;
end if;
end while;
// The matrix is now in row echelon form
// Set values of (h,k) to (m,n) h := m; k := n;
while h >= 1 and k >=1 loop
// Dealing with floating point errors
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
// Finding the pivot
pivot_row := {B[h,i] for i in 1:k};
// Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k := c;
// No pivot in this row, move on to next row
if B[h, k] == 0 then
h := h-1;
else
// Perform row operations
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] * r;
end for;
// Move on to next pivot row and column
h := h-1;
k := k-1;
end if;
end while;
// The matrix is now in reduced row echelon form
end GaussJordan;
PR 3
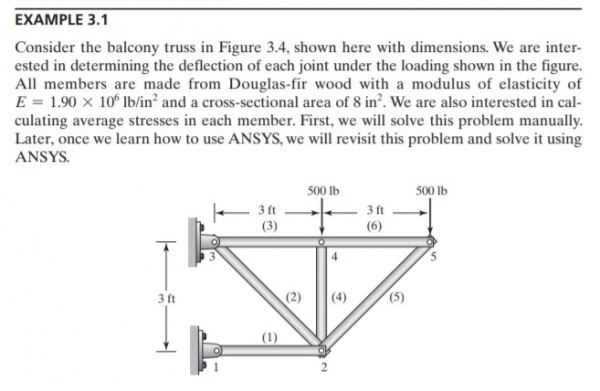
menyelesaikan 2 soal dengan open modelica yang berhubungan dengan engineering
problem 1 ( pada example 3.1)
*model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
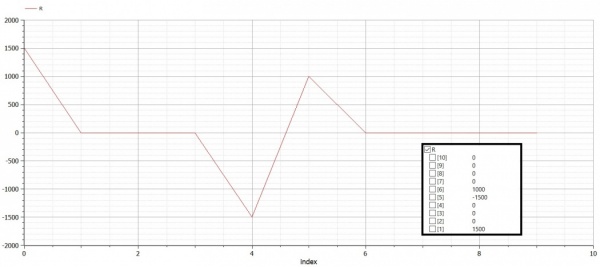
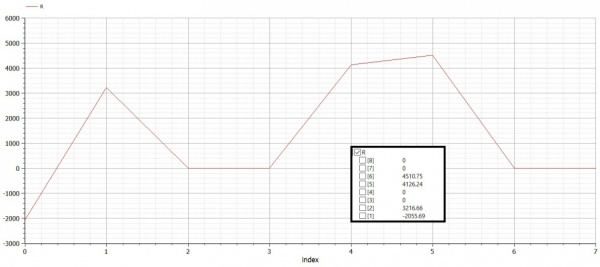
end Trusses;Grafik Reaction forces
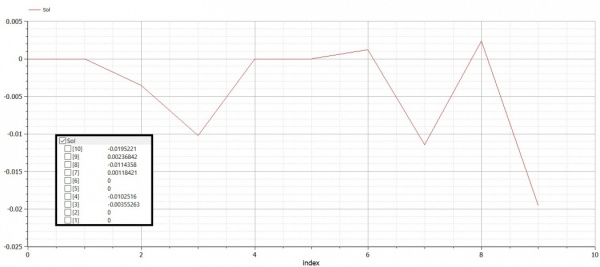
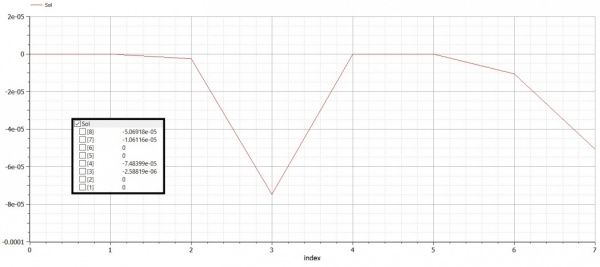
Grafik Diplacement
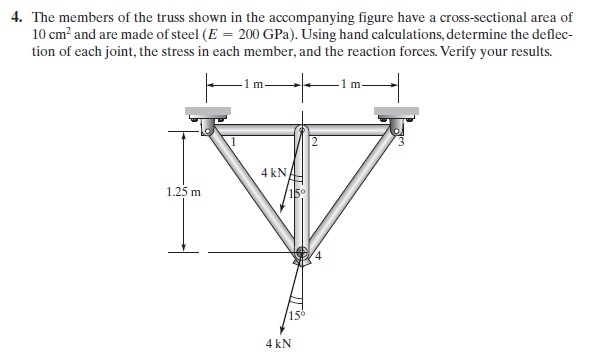
problem 2 ( PR NO 4 )
*class MetodeTrusses
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end MetodeTrusses;Grafik Reaction Process
Grafik Diplacement
Transformasi Matriks
function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;Global Element Matrice
function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
Reaction Matrice Equation
function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;
algorithm
X:=A*B-C;
for i in 1:N loop
if abs(X[i,1]) <= float_error then
X[i,1] := 0;
end if;
end for;
for i in 1:N loop
Sol[i]:=X[i,1];
end for;
end Reaction_Trusses;Gauss Jordan
function Gauss_Jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan;MINGGU KE 4
Kuis pada hari rabu tanggal 2 desember 2020
membuat diagram class dan flowchart dari fungsi yang telah dibuat josiah
KUIS DIAGRAM CLASS DAN FLOWCHART
Tugas Minggu ke 4
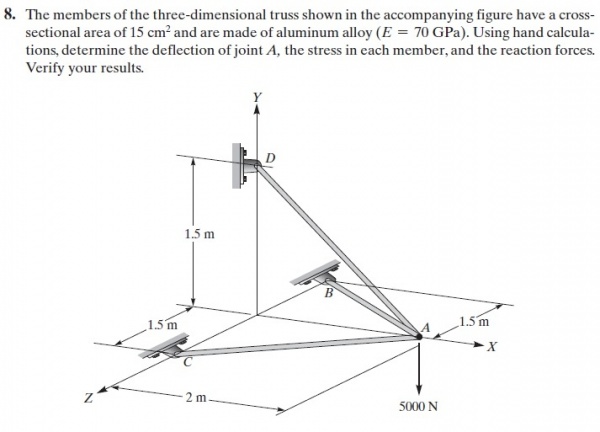
Pada tugas ke 4 kali ini , kami diberikan soal untuk menyelesaikan sebuah permasalahan mengenai space truss dengan membuat flowchart, diagram class, dan coding modelicanya.
jawab :
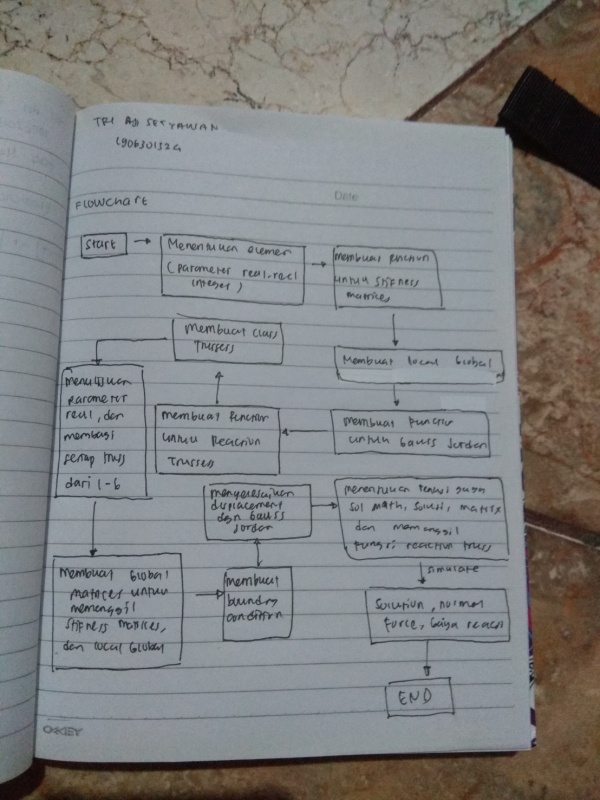
Pertama tama saya membuat flowchart dan diagram class. lalu saya membuat free body diagram dari sistem dan mencari data-data yang dibutuhkan.
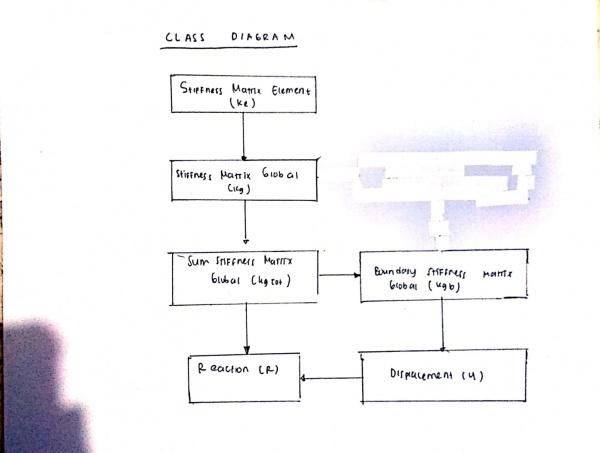
Class Diagram
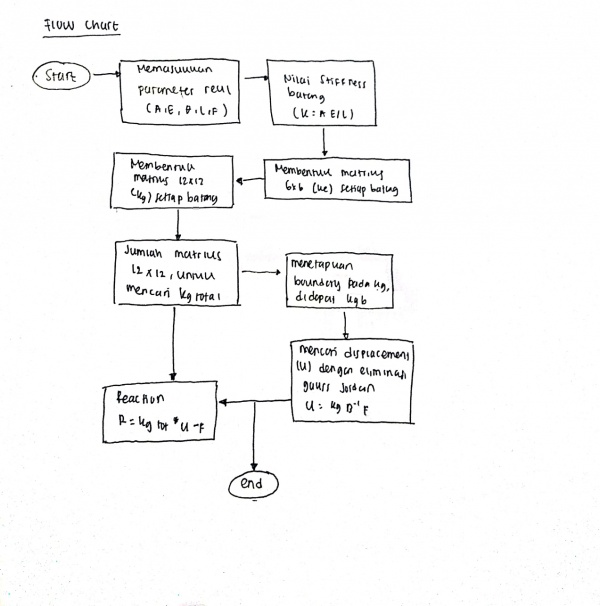
Flowchart
Setelah data-data sudah didapatkan lalu diproses ke dalam OpenModelica menggunakan referensi coding A. M. Fahmi.
Saya mencari k tiap element terlebih dahulu menggunakan rumus k=AE/L. Setelah itu bisa mencari nilai Ke.
function StiffnessMatrixElement
input Real [:,9] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real cos_z;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
// Converting degrees to radians
cos_x := inisiasi_mat[i,4];
cos_y := inisiasi_mat[i,5];
cos_z := inisiasi_mat[i,6];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;Membuat stiffness matrix global
function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal;Semua stiffness matrix global dijumlahkan dan didapatkan sum stiffness matrix global.
function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;menentukan boundaries pada sum stiffness matrix global.
function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
Untuk mencari nilai displacement (U) lainnya digunakan eliminasi Gauss Jordan dengan persamaan XU=F. Dimana X adalah stiffness matrix global yang sudah ditentukan boundarynya.
function GaussJordan
input Integer x;
input Real [x,x] KgB_met;
input Real [x] load_met;
output Real [x] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;kemudian mencari reaction menggunakan persamaan R=Kg*U - F.
function ReactionForce
input Integer x;
input Real [x,x] KgTot_met;
input Real [x] U_met;
input Real [x] load_met;
output Real [x] R_met;
algorithm
R_met := (KgTot_met*U_met)-load_met;
end ReactionForce;Selanjutnya, membuat sebuah Class untuk memanggil fungsi-fungsi diatas agar bisa melihat nilai U dan R.
class truss
parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5;
2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5;
3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {2,3,4};
parameter Real [:,4] node_load = [1, 0, -5000, 0;
2, 0, 0, 0;
3, 0, 0, 0;
4, 0, 0, 0];
parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
end truss;hasil dari U dan R
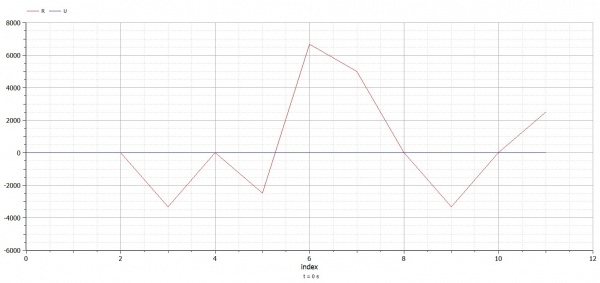
grafik
video penjelasan terkait penyelesaian soal no 8
Aplikasi Metode Numerik dalam Kasus Optimasi
Pada minggu ke 6 , kami mempelajari mengenai optimasi. sebelum kuliah dimulai, bu chandra memberikan penjelasan singkat mengenai optimasi dengan menggunakan bracket. Di akhir video , kami diperintahkan untuk mencoba perhitungan optimasi yang ada di video.
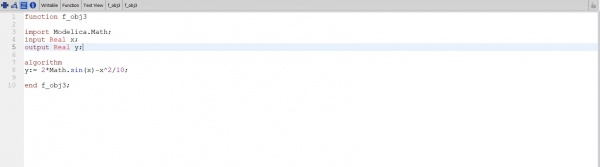
Membuat model untuk memanggil fungsi
Fungsi yang akan di panggil
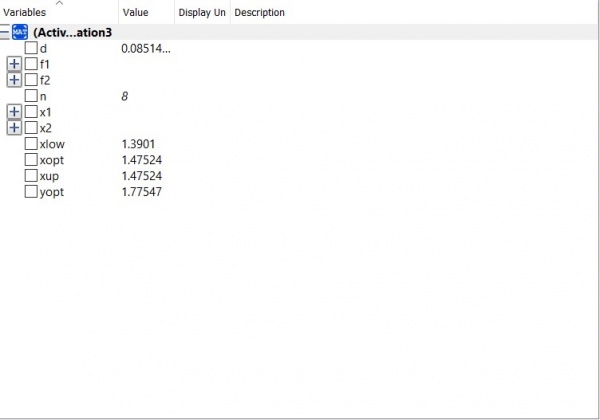
Hasil yang diperoleh
TUGAS BESAR METNUM
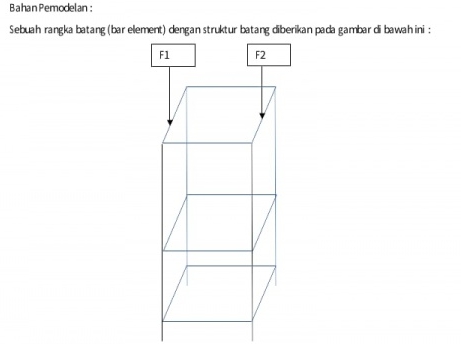
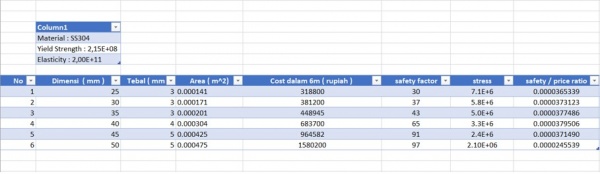
Pada tugas besar ini, kami diperimtahkan untuk mendesain rangka dengan menggunakan optimasi.
Dari soal tersebut kita diperintahkan untuk mendesain rangka batang dengan harga terjangkau dan optimal untuk fungsinya.
Yang perlu kita cari adalah Harga, Material yang digunakan, cross section Dilakukan dengan metode optimasi dan membentuk curve fitting pada variabel harga
Asumsi yang digunakan dalam perhitungan ini :
- Beban akan terdistribusi hanya pada node (karena bersifat trusses).
- Safety factor minimal bernilai 2.
- Batas displacement 0,001 m sebelum buckling (pada truss paling atas).
- Ketinggian trusses pada tiap lantai sama yaitu 0,6 m.
Untuk jenis material yang sama:
- Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu SS304 .
- Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting.
- Melakukan optimasi menggunakan metode golden section.
Untuk area penampang yang sama:
- Mencari harga untuk 3 jenis material dengan area penampang yang sama yaitu 171 mm^2.
- Mengitung nilai safety factor pada 3 jenis batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting.
- Melakukan optimasi menggunakan metode golden section.
Kemudian , saya akan menggunakan coding sebagai berikut untuk melakukan perhitugnan sehingga didapatkan reaction force , stress , displacement , dan safety factor ( yield / stress ).
Coding Yang akan digunakan
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000201; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=200e9; //Elasticity SS304 Stainless Steel (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;Membuat Kurva Curve Fitting
function Curve_Fitting
input Real X[:];
input Real Y[size(X,1)];
input Integer order=2;
output Real Coe[order+1];
protected
Real Z[size(X,1),order+1];
Real ZTr[order+1,size(X,1)];
Real A[order+1,order+1];
Real B[order+1];
algorithm
for i in 1:size(X,1) loop
for j in 1:(order+1) loop
Z[i,j]:=X[i]^(order+1-j);
end for;
end for;
ZTr:=transpose(Z);
A:=ZTr*Z;
B:=ZTr*Y;
Coe:=Modelica.Math.Matrices.solve(A,B);
end Curve_Fitting;Untuk Optimasi Golden Section
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;Material Tetap
Hasil Optimasi :
Nilai luas area penampang optimum untuk material SS304 adalah 0.000423422m^2.
Luas Truss Tetap
Hasil Optimasi :
Material optimum yang dapat digunakan untuk luas penampang 171mm^2 adalah material dengan nilai elastisitas sebesar 1.9697x10^11Pa, yaitu material SS304.
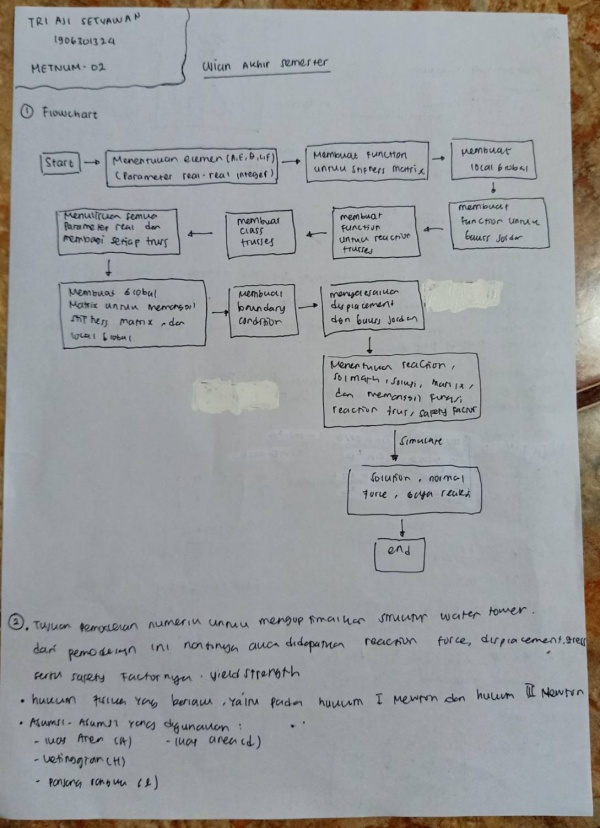
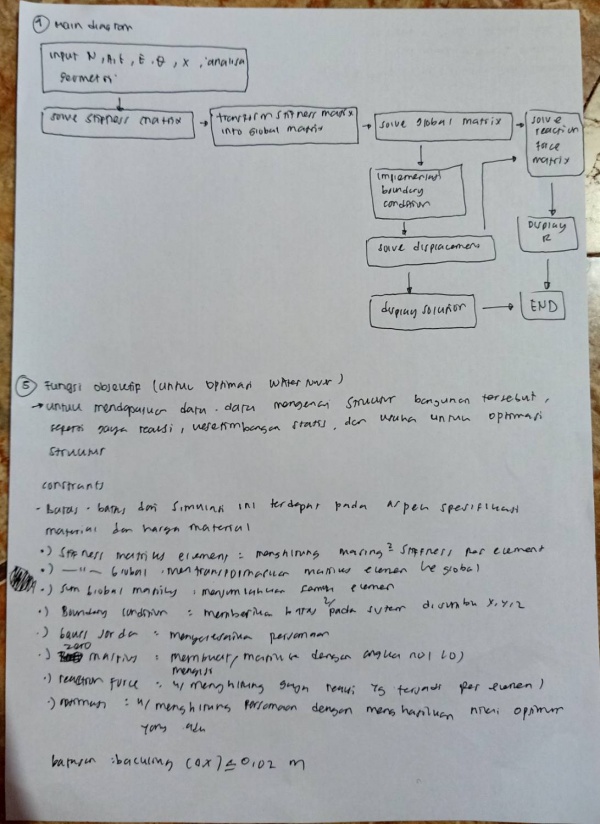
UJIAN AKHIR SEMESTER
Jawaban Uas
coding yang akan digunakan
model Uas_MetodeNumerik
//define initial variable
parameter Integer Points=4; //Number of Points
parameter Integer Trusses=3; //Number of Trusses
parameter Real Yield=214e6; //Yield Strength (Pa)
parameter Real Area=0.16; //Area Block Profile (0.4 * 0.4) (m2)
parameter Real Elas=207e9; //Elasticity SS 304 (Pa)
parameter Real Volume=1135; //m3 from 200000 gallons
parameter Real rho=1000; //kg/m3
parameter Real W=Volume*rho*9.81;
//define connection
parameter Integer C[Trusses,2]=[1,2;
2,3;
2,4];
//define coordinates (please put orderly)
parameter Real P[Points,3]=[0,37,0;
0,12,0;
-16,0,0;
16,0,0];
//define external force (please put orderly)
parameter Real F[Points*3]={0,-W,0,
0,0,0,
0,0,0,
0,0,0};
//define boundary
parameter Integer b[:]={3,4};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for i in boundary loop
for j in 1:N loop
G[i,j]:=id[i,j];
end for;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Uas_MetodeNumerik;